Элементарные излучатели электромагнитного поля. Электромагнитное поле плоских излучающих раскрывов

1.

Кафедра радиосвязи
ДИСЦИПЛИНА: ЭМП и В ( Д-1105-1 )
Тема 3. ЭЛЕМЕНТАРНЫЕ ИЗЛУЧАТЕЛИ ЭМ поля
Лекция 3/3 (№12). Электромагнитное поле
плоских излучающих раскрывов
Учебные
вопросы:
1. Принцип Гюйгенса-Кирхгофа.
2. Элемент Гюйгенса и его параметры.
3. Понятие о расчёте поля апертурных
излучателей.

2.

Типы излучателей ЭМ поля
а)
б)
г)
в)
Е
Е
Е
д)
№2
с)
Е
Кроме проволочных (линейных) излучателей существуют
излучатели со сложной поверхностью. Излучение в этом случае
происходит из раскрыва (апертуры) излучателя.
Для определения ЭМ поля таких излучателей необходимо найти
распределение тока на внутренней поверхности излучателя, что
очень сложно, поэтому применяют другие методы.

3.

1. Принцип Гюйгенса – Кирхгофа
№3
При расчете апертурных излучателей
применяют принцип Гюйгенса – Кирхгофа.
Согласно принципу Гюйгенса,
каждая точка фронта
распространяющейся волны
является источником новой
вторичной сферической волны.
Поэтому источники ЭМ поля
можно задавать или определять
не на самом излучателе, а на
любой замкнутой поверхности,
например апертуре (раскрыве)
излучателя.
чи
у
л
A
S1
S2
Этот процесс распространения, строго говоря, справедлив в
изотропной однородной среде.

4.

Суть метода расчета апертурных излучателей
№4
1) При решении внутренней задачи используется принцип
Гюйгенса и метод геометрической оптики, а на раскрыве
излучателя задаются эквивалентные источники
(поле Еs или токи).
2) При решении внешней задачи Кирхгофом впервые была дана
математическая формулировка определения поля в дальней
зоне с использованием эквивалентных источников в виде
элементов Гюйгенса.
Поэтому данный метод расчета поля получил название принцип
Гюйгенса – Кирхгофа.
ЭМ поле апертурных
излучателей
определяется, как сумма
элементов Гюйгенса:
E ( , )
S
dEпэГ
Апертура
S
П

5.

Эквивалентные источники поля
№5
В случае произвольной проводящей поверхности эквивалентными
источниками будут электрические и магнитные токи или
соответственно их поля.
Sбок Es 0
Сторонний
источник
Sкр Es 0
S n n
0
.
0
- внешняя нормаль
Es 0
,
0
0
J э n , H n , H S
J м n 0 , E n 0 , ES
Es
Hs
- это ГУ для идеального
проводника.
- это ГУ для идеального
диэлектрика.

6.

Методы задания эквивалентных
источников поля
№6
Вместо реальных источников поля на сложной внутренней
поверхности излучателя (например рупора) обосновано можно
задать эквивалентные источники только на раскрыве (апертуре)
излучателя .
Чаще всего на апертуре задают распределение напряженности
поля Еs.
В случае плоской
этой поверхности эквивалентные источники
.
задаются двумерной функцией распределения, что еще более
упрощает задачу определения
поля излучения (решения
,
внешней задачи электродинамики).
Наиболее простой путь интегрирований эквивалентных источников
в виде элементов Гюйгенса или других функций (Еs) по поверхности
раскрыва (апертуры) излучающей системы.
.

7.

2. Элемент Гюйгенса и его параметры
№7
Элемент Гюйгенса это виртуальный плоский элементарный
излучатель (элементарная плоская поверхность) эквивалентных
источников на поверхности фронта волны.
Сторонние токи:
J э n , H S ,
СТ
0
0
J м n , ES .
JЭ
Es
JM
Hs
СТ
n
l1
0 - внешняя нормаль
l2
Элемент Гюйгенса – это сумма 2-х ортогональных излучателей: ЭЭД
и ЭМД.

8.

Составляющие поля элемента Гюйгенса
а)
б)
z
r
S
Hs
Es
j
r
n
r Es H s j э j м
jм
z
y
jэ
l1
0
l2
M r , ,
м
jэ
x
№8
n 0 S
y
M
x
ES --вдоль оси Х
Элемент Гюйгенса излучает 2 составляющих вектора Е
E
E
E , E

9.

Суммарное поле элемента Гюйгенса
№9
ЭМ поле ЭГ – это сумма составляющих полей ЭЭД и ЭМД:
E ( , ) E
э
θ(φ)
E
м
θ(φ)
.
ikr
E
S
1
cos
e
э
м
S
E ( , ) E E i
cos
;
2 r
ikr
ES S
1 cos e
E ( , ) E E i
sin
,
2 r
E
E
H
;
H .
Zв
Zв
э
Для среды, где
1
м
Zв Zc 0 0 120 Ом.

10.

Электрические характеристики
элемента Гюйгенса
№10
Е - плоскость (это плоскость, где задан вектор Е или Еs)
E ( , 0) 0
E ( , 0) 0
Н – плоскость (ортогональная вектору Е)
E ( , 90 ) 0
0
E ( , 90 ) 0
0
Амплитуда суммарного поля не зависит от угла φ:
E ( ) E E
2
2
ES S
Нормированная Х.Н. :
r
Fэг ( ),
Fэг ( ) (1 cos ) 2.

11.

Диаграмма направленности
(сечение ДН)
№11
Нормированная функция
(характеристика направленности)
Fэг ( ) (1 cos ) 2 1
.
ДН элемента Гюйгенса
Элемент Гюйгенса имеет одностороннюю направленность
излучения.
Диаграмма направленности элемента Гюйгенса одинакова во всех

12.

Пространственная ДН элемента Гюйгенса
(3Д)
Пространственная ДН элемента Гюйгенса
осесимметричная в плоскости X-Y (относительно угла φ)
z
F ,
0
x
y
№12

13.

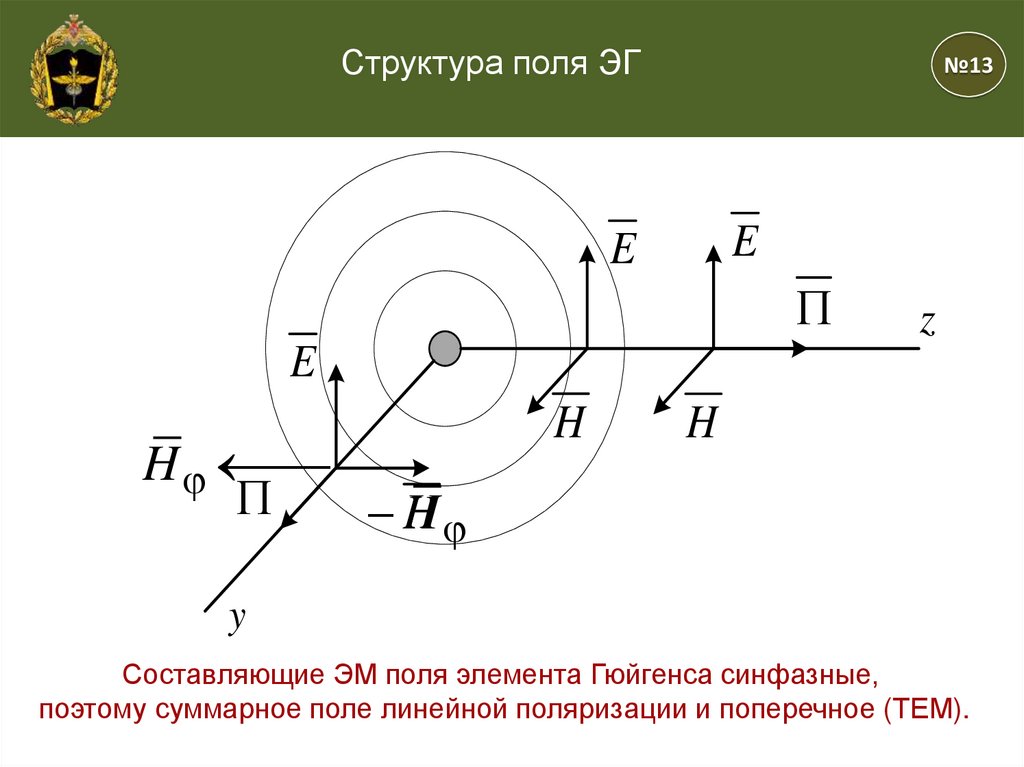
Структура поля ЭГ
№13
E
E
z
E
H
H
H
H
y
Составляющие ЭМ поля элемента Гюйгенса синфазные,
поэтому суммарное поле линейной поляризации и поперечное (ТЕМ).

14.

КНД элемента Гюйгенса
№14
КНД излучателей можно определить как отношение
величины вектора Пойнтинга в данном направлении
относительно среднего значения:
max
P
; П Emax
П
,
2.
ср
ср
max
2Z В
4 r
2
Dmax
2
Dmax
r
2
Emax ,
60 P
Dmax 3.
или
E ( ) max
ES S
Fэг ( )
r
D( , ) Dmax F ( , ).
2
КНД характеризует способность излучателя концентрировать
излученное ЭМ поле.

15.

Кардиоидные излучатели
№15
Элемент Гюйгенса является виртуальным излучателем.
Однако на практике применяют кардиоидные излучатели.
Такой излучатель можно реализовать в виде рамки малых размеров и
ЭЭД, расположеных в одной плоскости. Для этого необходимо
подобрать их размеры и способ питания.

16.

Кардиоидные ДН
№16

17.

3. Понятие о расчете поля апертурных
излучателей
(Метод Гюйгенса – Кирхгофа)
эГ
ЭМ поле в дальней зоне (области):
п
dE
E ( , )
S
z
М ( r , , )
Множитель сферической волны:
r x2 y 2 z 2
S в плоскости х-у
rn
Hs
Es
S n
rn ( x xn )2 ( y yn )2 z 2 .
y
0
x
.
r
S
№17
М (r ,90 , )
e ikrn , 1 1
rn
rn r
Амплитудный множитель
1/r = const.
Фазовый множитель
e
ikrn
Показатель экспоненты (фазовый множитель)
аппроксимируется выражением:
e
ikr ik rn
e
rn r rn .
rn r rn xn sin cos yn sin sin .
,

18.

Напряженность поля излучения
апертурной антенны
Составляющие ЭМ поля
элементов Гюйгенса
на раскрыве антенны:
cos
e ikr
E i
FЭГ ( )
r
sin
e ikr
E i
FЭГ ( )
r
№18
ikrn
cos
e
E i
FЭГ ( ) ES ( x, y)
dS ,
rn
S
sin
e ikrn
E i
FЭГ ( ) ES ( x, y )
dS .
rn
S
ik r
E
(
x
,
y
)e
dS ,
S
S
ik r
E
(
x
,
y
)e
dS.
S
S
FЭГ ( ) (1 cos ) 2,
Es - задается на раскрыве
Множитель системы
в декартовых координатах
Fc ( , ) ES ( x, y)e
ik r
dxdy.
S
Таким образом, необходимо определять только множитель системы.

19.

Пример излучения из прямоугольного
раскрыва
x
М (θ,φ)
Интегрирование в
декартовых координатах
r
Es
E
dS
b
№19
z
S
i
E
1 cos cos( ) Es eik rn dSn ,
2 ir0
SA
E
y
a
где:
2 r0
ik rn
1
cos
sin(
)
E
e
s dSn ,
Fc θ,
SA
ES eik rn dSn ,
SA
rn xn sin cos yn sin sin .
В прямоугольной апертуре интеграл выражается через
тригонометрические функции.

20.

Пример излучение из круглого раскрыва
x
Интегрирование в
полярной системе координат
2 a
Fc ( ) Es e
M(r,θ,φ)
φ
ЭИ
ik rs
dS ,
r
z
0
rs s sin cos( s ),
rn
θ
ES
0 0
dS s d s d s .
№20
SA
y
раскрыва (элемент Гюйгенса) в
dS элемент поверхности
полярной системе координат,
s расстояние от центра до произвольной точки в раскрыве.
В круглой апертуре интеграл выражается через
цилиндрические функции.

21.

ВЫВОДЫ
№21
Таким образом, при определении поля излучения плоских
излучающих раскрывов фактически необходимо выполнить двойное
интегрирование множителя системы эквивалентных источников в виде
элементов Гюйгенса.
Однако изложенный метод позволяет получить ЭМ поле плоской
излучающей системы только в пределах 90 град. от главного
направления, так как сам принцип Гюйгенса не дает объяснения
обратного излучения.
Для расчета поля по всему пространству вокруг излучающей
системы используются более строгие методы, основанные на
дифракции ЭМ волн.