Похожие презентации:
Прямая призма. Решение задач
1. Прямая призма
ПРЯМАЯ ПРИЗМАРешение задач
2.
B1A1
B
A
а) вершины;
C1
б) основания;
в) боковые ребра;
г) боковые грани;
D1 д) противоположные
грани;
C
е) диагонали граней;
ж) диагонали призмы;
и) диагональные
D
сечения.
3.
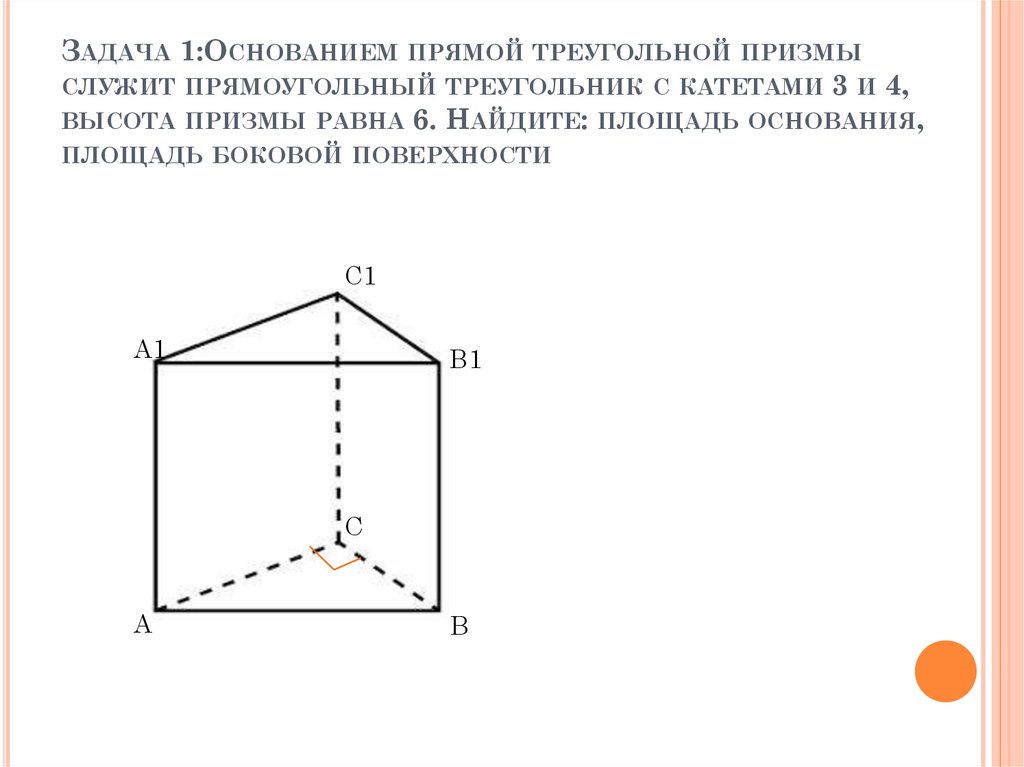
ЗАДАЧА 1:ОСНОВАНИЕМПРЯМОЙ ТРЕУГОЛЬНОЙ ПРИЗМЫ
СЛУЖИТ ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК С КАТЕТАМИ
ВЫСОТА ПРИЗМЫ РАВНА
6. НАЙДИТЕ: ПЛОЩАДЬ ОСНОВАНИЯ,
ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ
С1
А1
В1
С
А
3 И 4,
В
4.
Задача 2:В прямоугольном параллелепипеде с высотой 6 см,стороны основания равны 2 см и 3 см. Найти площадь
полной поверхности.
B1
C1
A1
D1
6
Sбок Pосн Н
Pосн AB AD 2
Pосн 2 3 2
Sбок 10 6
S полн Sбок 2Sоcн
Sосн AB AD
B
C
2
A
3
D
Sосн 3 2
S полн 60 12
5.
B1C1
A1
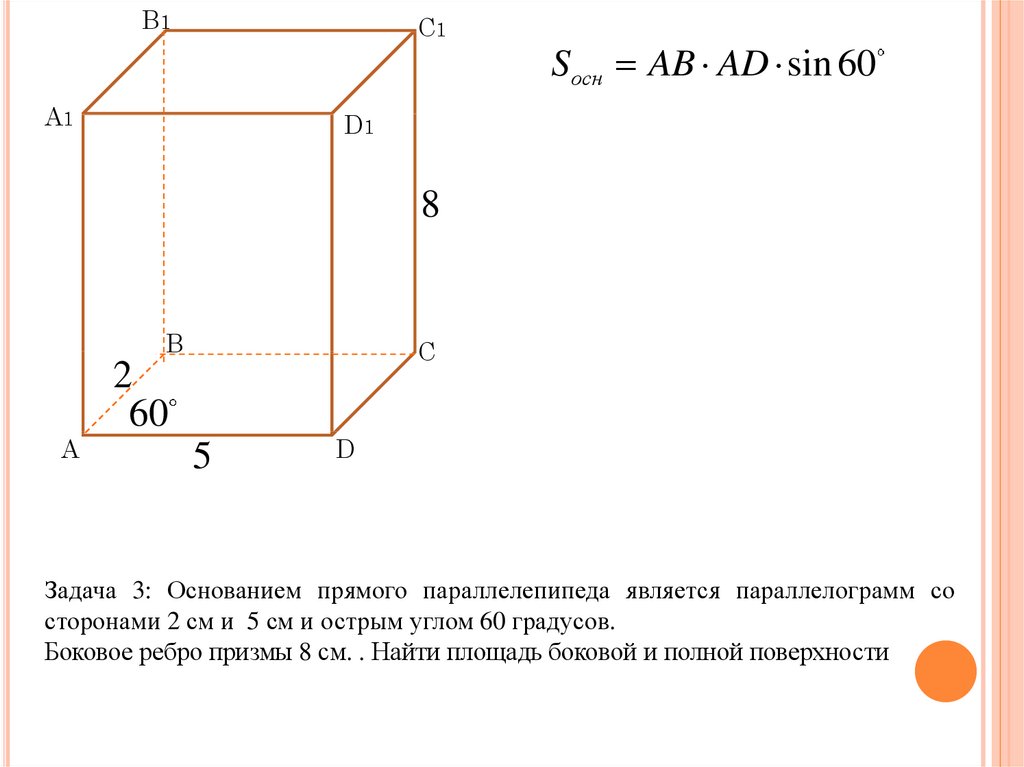
Sосн AB AD sin 60
D1
8
B
A
C
2
60
5
D
Задача 3: Основанием прямого параллелепипеда является параллелограмм со
сторонами 2 см и 5 см и острым углом 60 градусов.
Боковое ребро призмы 8 см. . Найти площадь боковой и полной поверхности
6.
Задача 4: В правильной треугольной призме длины всех ребер4 см. . Найти площадь боковой и полной поверхности
C1
4
4
A1
B1
C
A
4
Sбок Pосн Н
Pосн AB BC AC
Pосн 4 3
4
Sбок 12 4
Sполн Sбок 2Sоcн
B
Sосн
S полн 48 8 3
а2 3
4
Sосн 4 3
7.
Задача 5:Стороны основания прямого параллелепипеда 2 и 5 см иугол между ними 60 град. Известна меньшая диагональ
параллелепипеда. Найти площадь боковой, полной поверхности и
объем параллелепипеда
B1
C1
A1
D1
55
2
B
C
60
A
.
.
D
5
Из ΔABD по теореме косинусов найдем BD.
BD AB
AD
2
AB
AD
cos
A
2
2
2
2
2
2
BD 2 5 2 2 5 cos 60
BD=19
8.
Sбок Pосн НPосн AB AD 2
Pосн 5 2 2
Sбок 14 6
Sосн AB AD sin 60
Sосн
3
2 5
5 3
2
Sполн Sбок 2Sоcн
9.
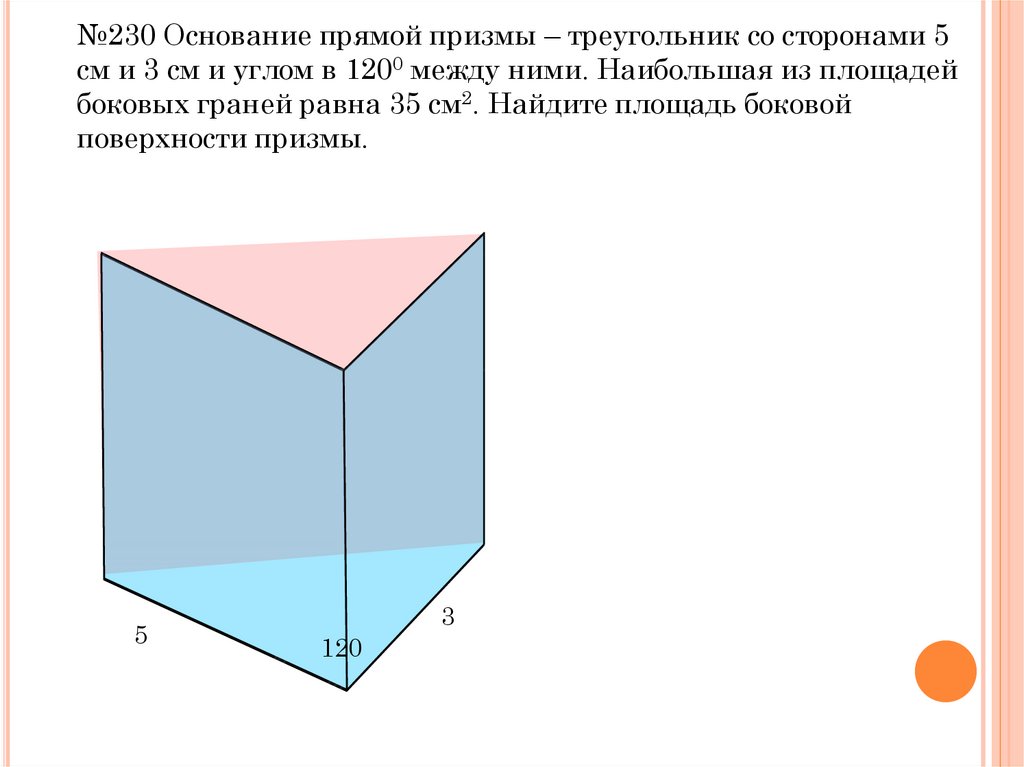
№230 Основание прямой призмы – треугольник со сторонами 5см и 3 см и углом в 1200 между ними. Наибольшая из площадей
боковых граней равна 35 см2. Найдите площадь боковой
поверхности призмы.
5
3
120





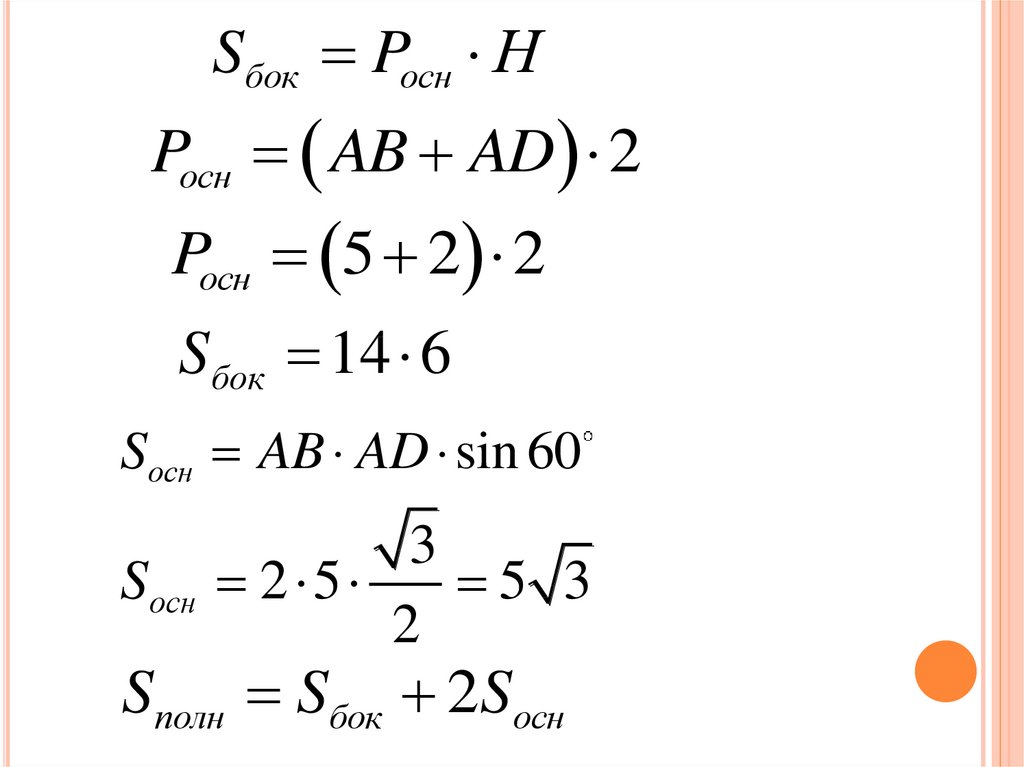
 Математика
Математика








