Похожие презентации:
Параллелепипеды и призмы
1.
2.
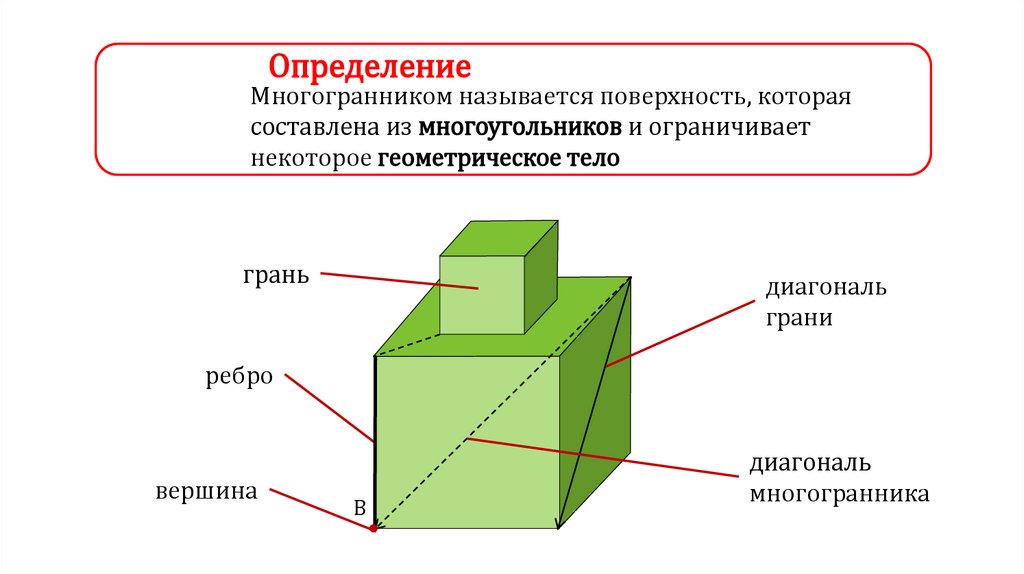
ОпределениеМногогранником называется поверхность, которая
составлена из многоугольников и ограничивает
некоторое геометрическое тело
грань
диагональ
грани
ребро
вершина
B
диагональ
многогранника
3.
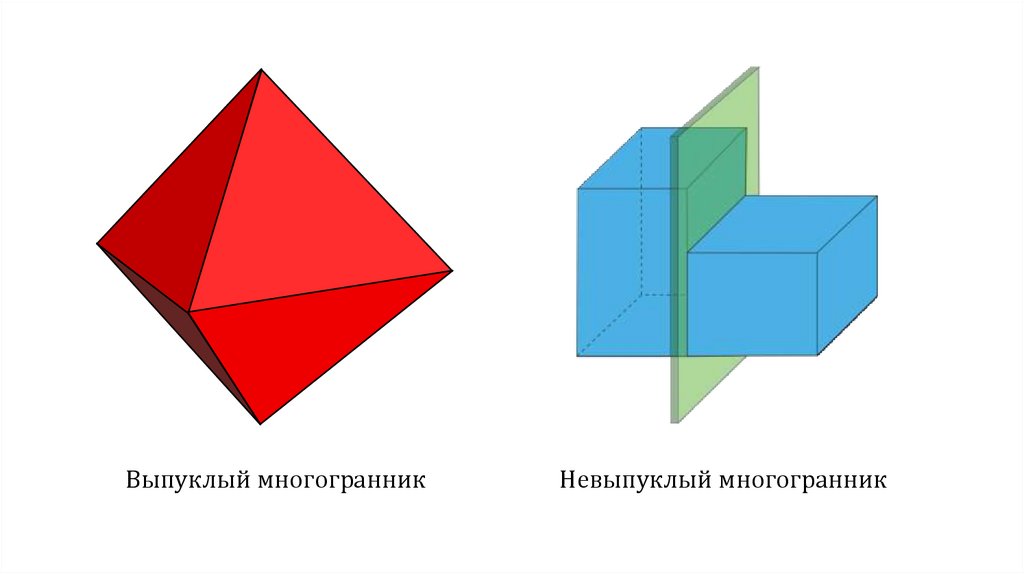
Выпуклый многогранникНевыпуклый многогранник
4.
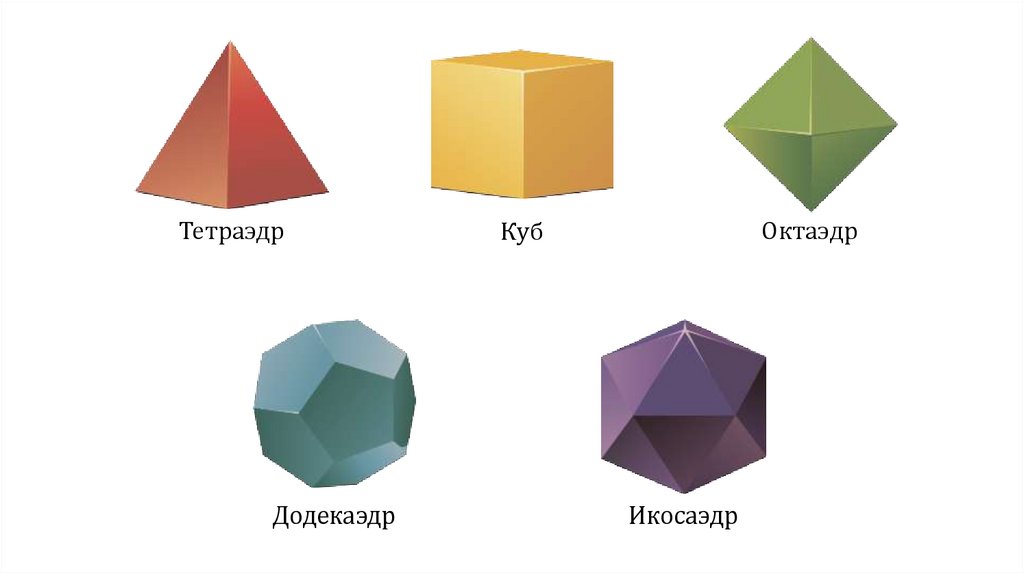
ТетраэдрДодекаэдр
Куб
Октаэдр
Икосаэдр
5.
Строительныйкирпич
Игральный
кубик
Микроволновая
печь
6.
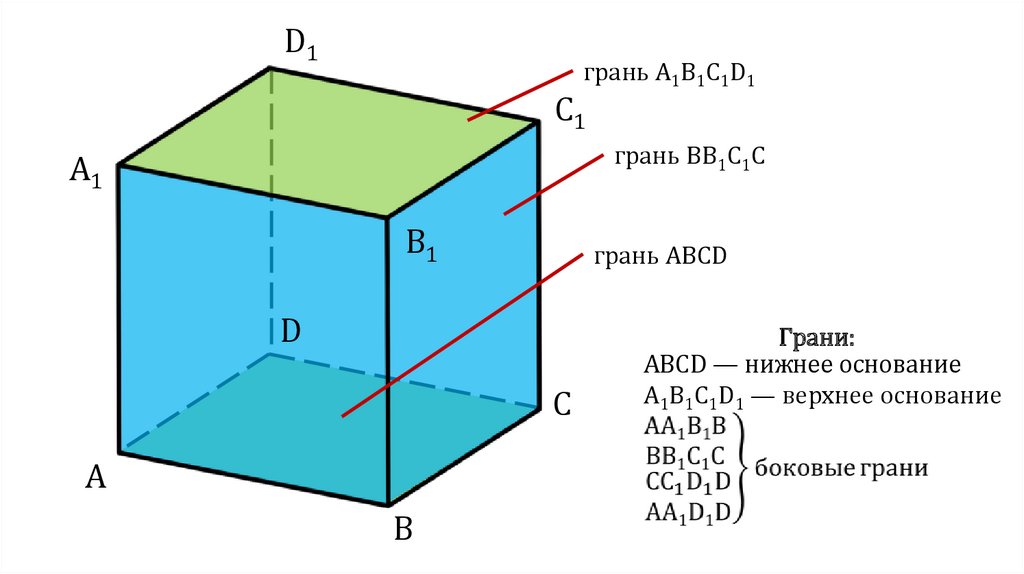
D1грань A1B1C1D1
C1
грань BB1C1C
A1
B1
грань ABCD
D
C
A
B
Грани:
ABCD — нижнее основание
A1B1C1D1 — верхнее основание
7.
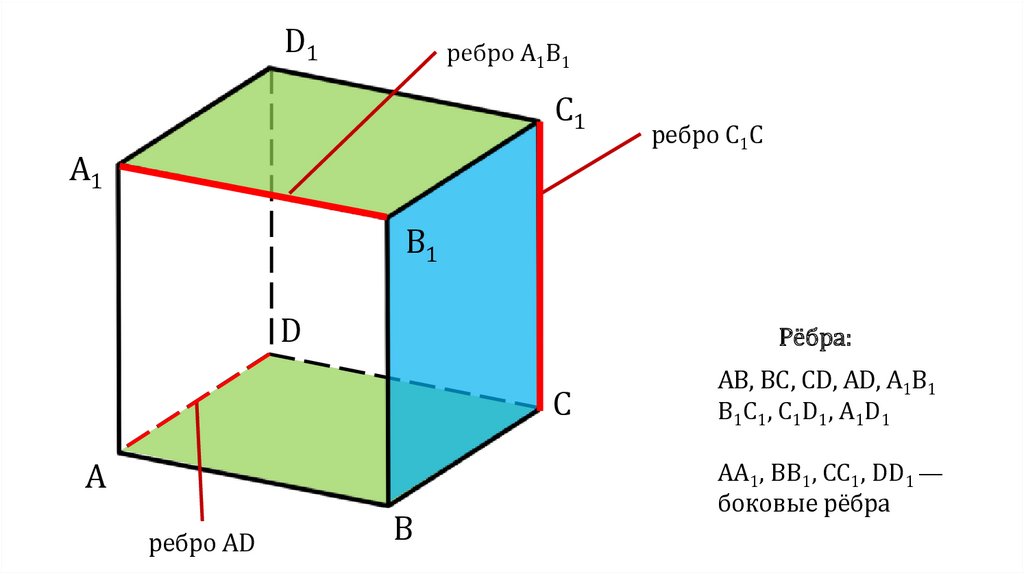
D1ребро A1B1
C1
ребро C1C
A1
B1
D
Рёбра:
C
A
ребро AD
B
АВ, ВС, CD, AD, А1В1
В1С1, C1D1, A1D1
АА1, ВВ1, СС1, DD1 —
боковые рёбра
8.
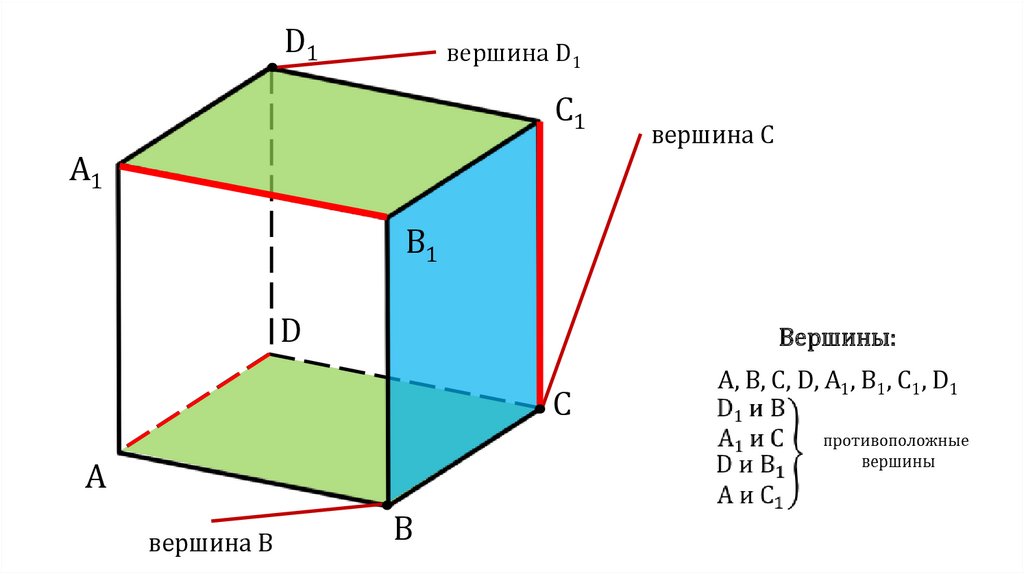
D1вершина D1
C1
вершина С
A1
B1
D
Вершины:
C
A
вершина B
B
А, В, С, D, А1, В1, С1, D1
9.
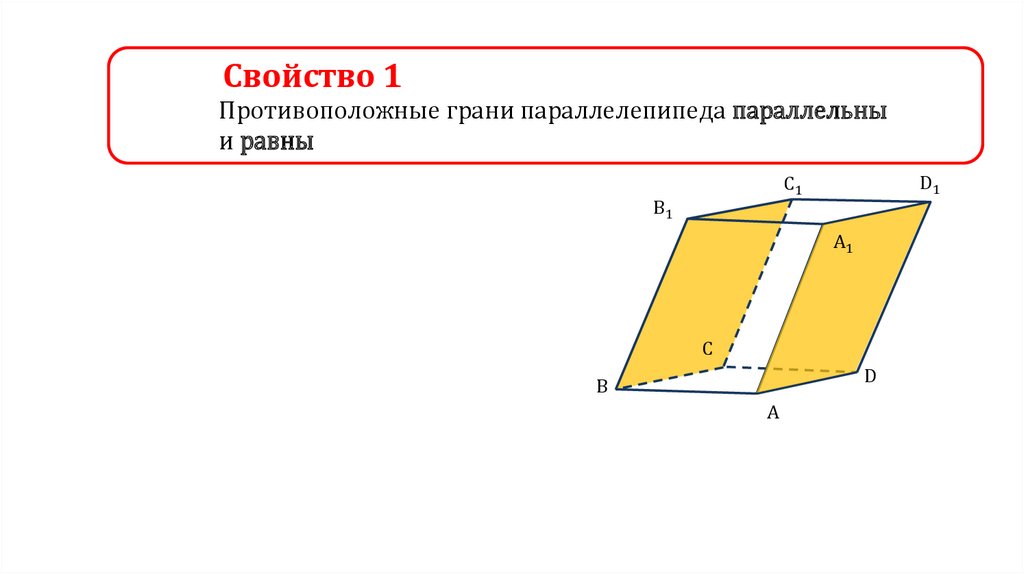
Свойство 1Противоположные грани параллелепипеда параллельны
и равны
D1
C1
B1
A1
C
D
B
A
10.
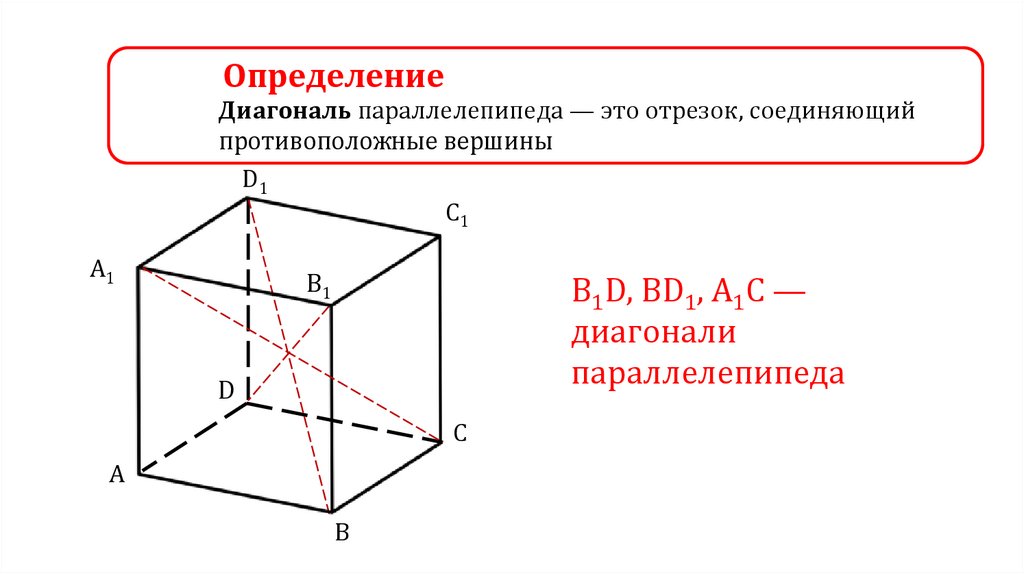
ОпределениеДиагональ параллелепипеда — это отрезок, соединяющий
противоположные вершины
D1
C1
A1
B1
В1D, BD1, А1С —
диагонали
параллелепипеда
D
C
A
B
11.
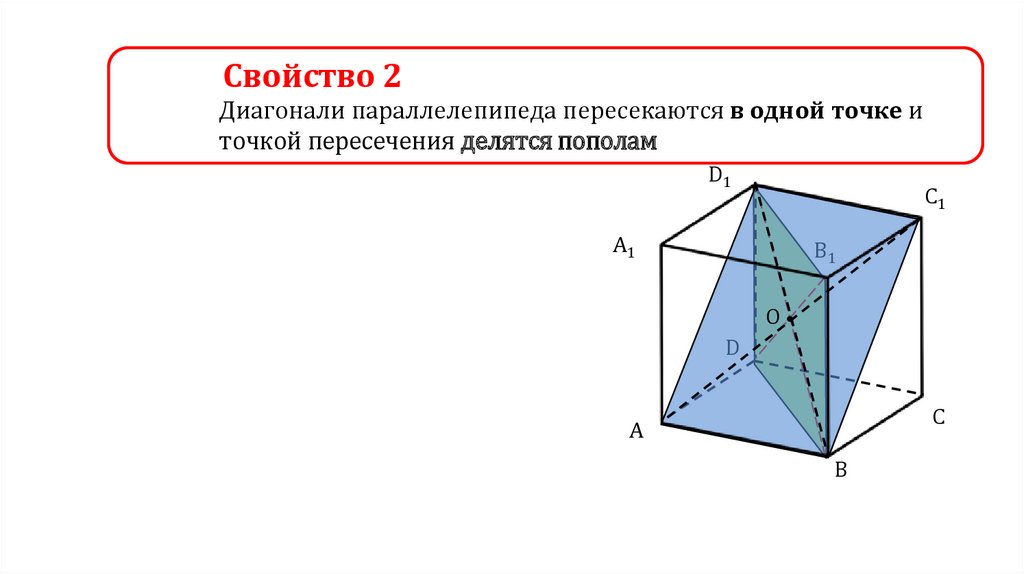
Свойство 2Диагонали параллелепипеда пересекаются в одной точке и
точкой пересечения делятся пополам
D1
C1
A1
B1
O
D
C
A
B
12.
αβ
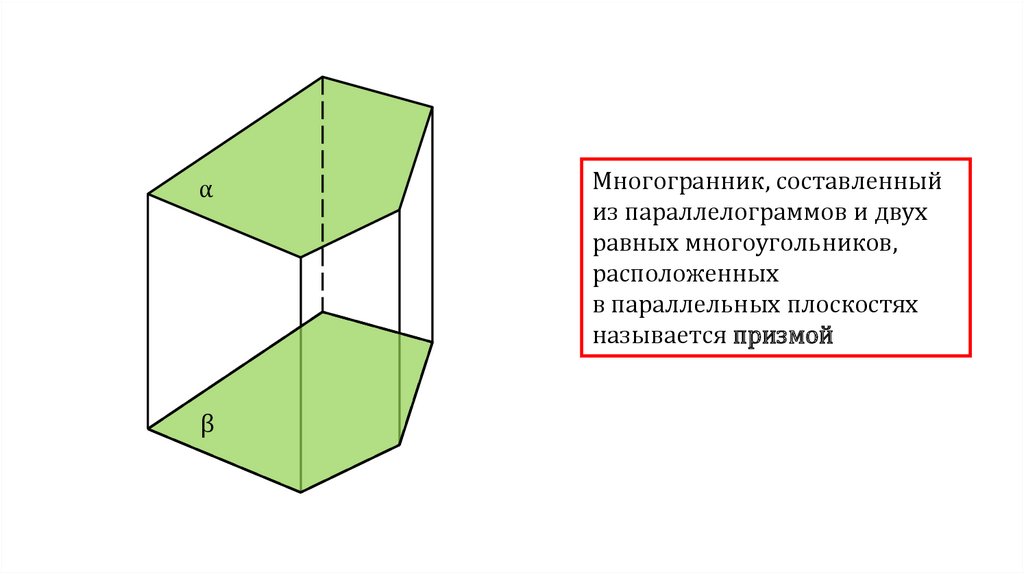
Многогранник, составленный
из параллелограммов и двух
равных многоугольников,
расположенных
в параллельных плоскостях
называется призмой
13.
A1C1
B1
основания
боковая грань
высота
C
A
боковое ребро
B
АВСA1B1C1 — треугольная призма
14.
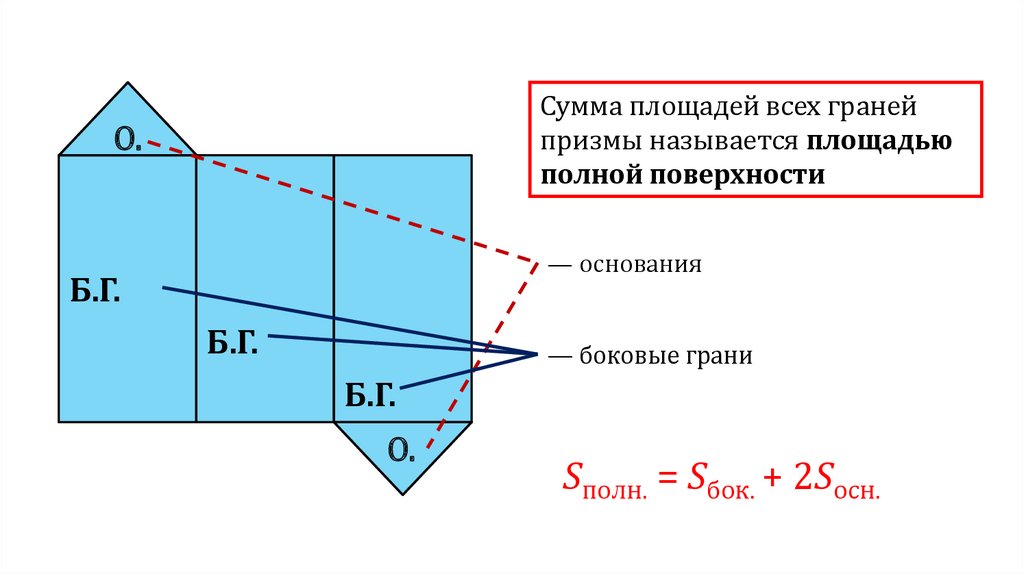
Сумма площадей всех гранейпризмы называется площадью
полной поверхности
О.
— основания
Б.Г.
Б.Г.
— боковые грани
Б.Г.
О.
Sполн. = Sбок. + 2Sосн.
15.
ТеоремаПлощадь боковой поверхности прямой призмы равна
произведению высоты призмы на периметр её основания
h
a3
a1
a2
16.
ТеоремаОбъем прямой призмы равен произведению высоты призмы
на площадь её основания
h
a3
a1
a2
V = Sосн. *H
17.
Задача 1.Вычислить объем прямой призмы, если высота призмы
равна 5см, а площадь её основания равна 15см.квадратных.
ДАНО: прямая призма,
S=15 cм^2
H = 5 cм
НАЙТИ: V?
h
РЕШЕНИЕ:
1) анализ:
V = Sосн. *H
2) V = 15*5 = 75 cм^3.
Ответ: V = 75 cм^3
S
18.
Задача 2.Вычислить площадь боковой поверхности прямой
треугольной призмы , если высота призмы равна 10см, а
стороны её основания равны 3, 4 и 7см.
ДАНО: прямая призма,
a=3, b=4см, с=7см.
h = 10 cм
НАЙТИ: Sбок?
h=10см
РЕШЕНИЕ:
1) анализ:
Sбок = Pосн. *H P = a+b+c
2) P=3+4+7 = 14см.
3) Sбок = 14*10 = 140см^2.
Ответ: Sбок = 140cм^2.
7см
4см
3см
19.
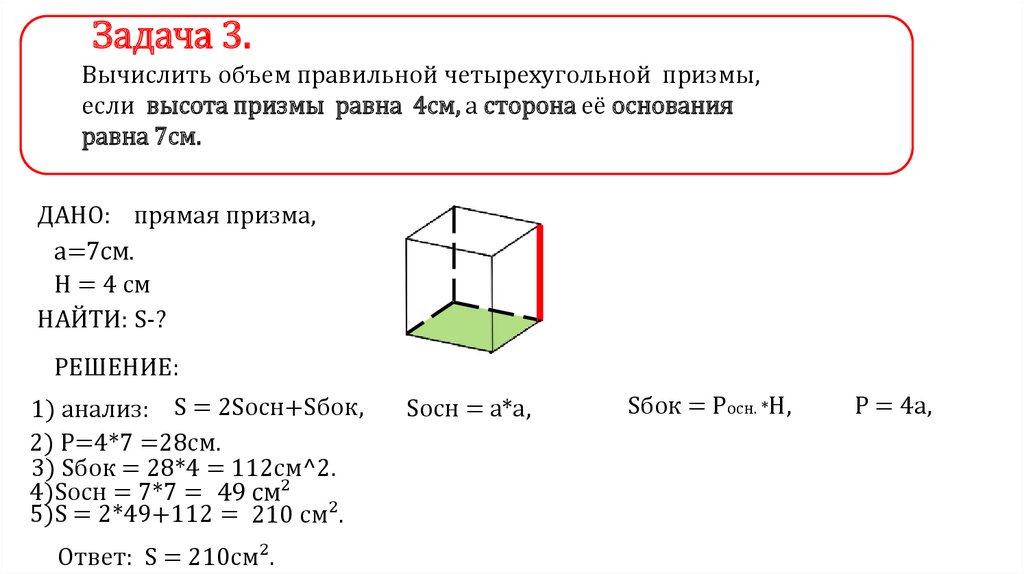
Задача 3.Вычислить объем правильной четырехугольной призмы,
если высота призмы равна 4см, а сторона её основания
равна 7см.
ДАНО: прямая призма,
а=7см.
H = 4 cм
НАЙТИ: S-?
РЕШЕНИЕ:
1) анализ: S = 2Sосн+Sбок,
2) P=4*7 =28см.
3) Sбок = 28*4 = 112см^2.
4)Sосн = 7*7 = 49 см²
5)S = 2*49+112 = 210 см².
Ответ: S = 210cм².
Sосн = a*a,
Sбок = Pосн. *H,
P = 4а,
20.
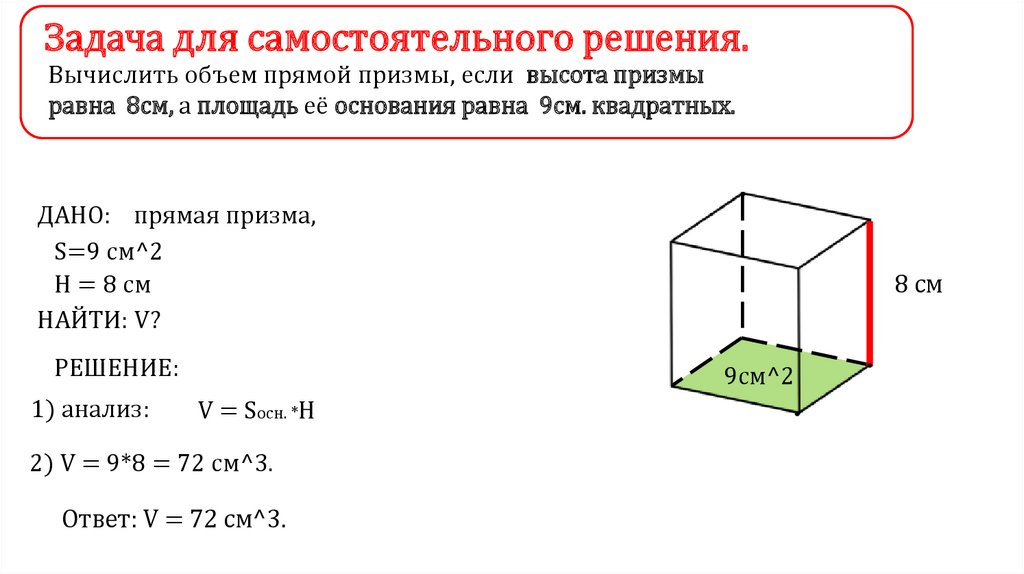
Задача для самостоятельного решения.Вычислить объем прямой призмы, если высота призмы
равна 8см, а площадь её основания равна 9см. квадратных.
ДАНО: прямая призма,
S=9 cм^2
H = 8 cм
НАЙТИ: V?
РЕШЕНИЕ:
1) анализ:
8 см
9cм^2
V = Sосн. *H
2) V = 9*8 = 72 cм^3.
Ответ: V = 72 cм^3.







 Математика
Математика