Понятие первообразной. Таблица первообразных. Правила нахождения первообразных

1. Понятие первообразной. Таблица первообразных. Правила нахождения первообразных.

Уярский сельскохозяйственный
техникум
08.05.2020
1

2.

Необходимо знать и уметь:
-знать и уметь использовать формулы и правила
дифференцирования;
http://ta-shah.ucoz.ru/load/10_klass/10_klass/formuly_i_pravila_differencirovanija/12-1-0-38
http://ta-shah.ucoz.ru/load/10_klass/10_klass/differencirovanie_slozhnoj_funkcii/12-1-0-41
- уметь выполнять преобразования алгебраических
и тригонометрических выражений.
08.05.2020
2

3.

Функция F(x)называется первообразной для функции
f(x)на некотором промежутке, если для всех x из этого
промежутка F ( x ) f ( x ).
Задача №1. Докажите, что функция F(x) является
первообразной для функции f(x).
1)
1
Воспользуемся определением
f(x) 2
x
Если F ( x ) f ( x )
1
F ( x ) первообразная для
F( x )
x
Найдем F'(x)
f( x)
1
1
1
1
F ( x ) 1 1 2 2 f ( x )
x
x
x x
F ( x ) первообразная для f ( x )
08.05.2020
Формулы и правила
4
дифференцирования

4.

Функция F(x)называется первообразной для функции
f(x)на некотором промежутке, если для всех x из этого
промежутка F ( x ) f ( x ).
Задача №1. Докажите, что функция F(x) является
первообразной для функции f(x).
2) f ( x ) 2 x 3 x 2 3 cos x
F ( x ) x 2 x 3 3 sin x 1
F ( x ) ( x 2 x 3 3 sin x 1 )
( x 2 ) ( x 3 ) 3(sin x ) ( 1 )
2 x 3 x 2 3 cos x 0 2 x 3 x 2 3 cos x f ( x )
F ( x ) первообразная
08.05.2020
для
f( x)
Формулы и правила
5
дифференцирования

5.

Функция F(x)называется первообразной для функции
f(x)на некотором промежутке, если для всех x из этого
промежутка F ( x ) f ( x ).
Задача №1. Докажите, что функция F(x) является
первообразной для функции f(x).
3)
3 x
1 1 3
3
2
F ( x ) 3 x
f(x) 2 x
x 3
x 3
x
3
3 x
F( x )
1 1
1 1 3
2
3
3
x
x 3 3 ( x )
2
x 3
x 3
3
2 x2 f ( x )
x
F ( x ) первообразная для f ( x )
3
08.05.2020
Формулы и правила
6
дифференцирования

6.

Функция F(x)называется первообразной для функции
f(x)на некотором промежутке, если для всех x из этого
промежутка F ( x ) f ( x ).
Задача №1. Докажите, что функция F(x) является
первообразной для функции f(x).
4)
2
2
2
F
(
x
)
4
x
tgx
f(x)
2
3
x 3 cos x
2
2
F ( x ) 4 x tgx
4 ( x ) ( tgx )
3
3
1
2
1
2
2
f(x)
4
2
2
2 x 3 cos x
x 3 cos x
F ( x ) первообразная
08.05.2020
для
f( x)
Формулы и правила
7
дифференцирования

7.

Функция F(x)называется первообразной для функции
f(x)на некотором промежутке, если для всех x из этого
промежутка F ( x ) f ( x ).
Задача №1. Докажите, что функция F(x) является
первообразной для функции f(x).
F ( x ) cos 4 x 1
9
cos 4 x ( 1 )
9
sin 4 x 4 x 0 4 sin 4 x f ( x )
9
9
9
5) f ( x ) 4 sin 4 x
9
F ( x ) cos 4 x 1
9
F ( x ) первообразная
08.05.2020
для
f( x)
Формулы и правила
8
дифференцирования

8.

Функция F(x)называется первообразной для функции
f(x)на некотором промежутке, если для всех x из этого
промежутка F ( x ) f ( x ).
Задача №1. Докажите, что функция F(x) является
первообразной для функции f(x).
2x 3
6
2
F ( x ) x 3x
x
6
2
( x 3x )
x
1
1
1
1
2
( 2x 3 ) 6 2
( x 3x ) 6
2
2
x
2 x 3x
x
2 x 3x
2x 3
6
2 f(x)
2
2 x 3x x
F ( x ) первообразная для f ( x ) Формулы и правила
6
2
2
2 x 3x x
6
2
F( x ) x 3x
x
6) f ( x )
08.05.2020
9
дифференцирования

9.

Функция F(x)называется первообразной для функции
f(x)на некотором промежутке, если для всех x из этого
Формулы и правила
промежутка F ( x ) f ( x ).
дифференцирования
Воспользовавшись формулами дифференцирования и
Убедитесь
в правильности
составленной
таблицы.
определением
первообразной
можно
легко составить
таблицу
Найдите
F'(x).
первообразных для некоторых
функций.
f(x)
0
1
x
x r r 1
1
x2
x 0
F( x )
f(x)
С
x
x2
2
x r 1
r 1
1
x
1
x
F( x )
x 0
2 x
sin x
cos x
cos x
sin x
1
sin x 0
sin2 x
1
cos x 0
2
cos x
ctgx
tgx
10

10.

Для нахождения первообразных нам понадобятся
кроме таблицы правила нахождения первообразных.
1) Если F(x)– первообразная для функции f(x), а G(x)–
первообразная для функции g(x), то F(x)+G(x)– первообразная
для функции f(x)+g(x).
Первообразная суммы равна
сумме первообразных
2) Если F(x)– первообразная для функции f(x),
а а –константа, то аF(x)– первообразная
для функции аf(x).
Постоянный множитель можно
выносить за знак первообразной
3) Если F(x) – первообразная для функции f(x), а k и b1
константы, причем k≠0, то F ( kx b )- первообразная для
k
функции f ( kx b ).
08.05.2020
Назад
12

11.

Задача №2. Дана функция f(x). Найдите ее первообразную,
воспользовавшись таблицей первообразных и правилами
нахождения первообразной и выполните проверку,
Таблица
воспользовавшись определением (задача №1)
1)
2
f(x) 2
x
F( x ) ?
первообразных
В таблице такой функции нет.
Коэффициент
Преобразуем
f(x):
Табличная
2
1
f( x) 2 2 2
x
x
2
1
F( x ) 2
x
x
Правила
функция
Используем таблицу
и второе правило.
2
2
1
1
Проверка: F ( x ) 2 2 2 2 f ( x )
x
x
x x
F ( x ) первообразная
08.05.2020
для
f( x)
Формулы и правила
дифференцирования

12.

Задача №2. Дана функция f(x). Найдите ее первообразную,
воспользовавшись таблицей первообразных и правилами
нахождения первообразной и выполните проверку,
Таблица
воспользовавшись определением (задача №1)
2)
f(x)
первообразных
1
В таблице такой функции нет.
Коэффициент
f(x):
2 x Преобразуем
Табличная
F( x ) ?
1 1
f(x)
2 x 2 x
1
F( x ) 2 x
2
1
функция
Используем таблицу
и второе правило.
x
Проверка: F ( x ) ( x )
1
f(x)
2 x
F ( x ) первообразная для
08.05.2020
Правила
f( x)
Формулы и правила
дифференцирования

13.

Задача №2. Дана функция f(x). Найдите ее первообразную,
воспользовавшись таблицей первообразных и правилами
нахождения первообразной и выполните проверку,
Таблица
воспользовавшись определением (задача №1)
3)
f( x) x x
F( x ) ?
2
16
Табличная
функция
Табличная
функция
Используем таблицу
и первое правило.
первообразных
Правила
x 2 1
x 16 1
x 3 x 17
F( x )
2 1 16 1
3
17
x
1 3 1
x
Проверка: F ( x )
( x )
( x 17 )
3
17
17
3
1
1
2
16
2
3x
17 x 16 x x f ( x )
3
17
3
F ( x ) первообразная
08.05.2020
17
для
f( x)
Формулы и правила
дифференцирования

14.

Задача №2. Дана функция f(x). Найдите ее первообразную,
воспользовавшись таблицей первообразных и правилами
нахождения первообразной и выполните проверку,
Коэффициентопределением
Коэффициент (задача №1)
Таблица
воспользовавшись
4)
первообразных
f ( x ) 3 sin x 2 cos x
F( x ) ?
Табличная
функция
Используем таблицу,
первое и второе правило.
Табличная
F( x )
функция
Правила
3( cos x ) 2 sin x
3 cos x 2 sin x
Проверка: F ( x ) ( 3 cos x 2 sin x ) 3 sin x 2 cos x f ( x )
F ( x ) первообразная
08.05.2020
для
f( x)
Формулы и правила
дифференцирования

15.

Задача №2. Дана функция f(x). Найдите ее первообразную,
воспользовавшись таблицей первообразных и правилами
нахождения первообразной и выполните проверку,
Таблица
воспользовавшись определением (задача №1)
5)
первообразных
4
1
В таблице таких функций
нет.
Коэффициент
Коэффициент
f(x)
sin2 x 2 cos 2 x Преобразуем f(x):
1
1
1
F( x ) ?
f(x) 4
sin2 x 2 cos 2 x
Используем таблицу, первоеТабличная
и второе правило.
Правила
Табличная
функция
функция
1
1
F ( x ) 4 ( ctgx ) tgx 4 ctgx tgx
2
2
Проверка:
1
1
1
4
1
1
2
F ( x ) 4 ctgx tgx 4 2
2
2
sin x 2 cos x sin x 2 cos x
2
f ( x ) F ( x ) первообразная для f ( x )
Формулы и правила
08.05.2020
дифференцирования

16.

Задача №2. Дана функция f(x). Найдите ее первообразную,
воспользовавшись таблицей первообразных и правилами
нахождения первообразной и выполните проверку,
Таблица
воспользовавшись определением (задача №1)
первообразных
6)
f ( x ) sin( 3 x ) Синус – табличная функция.
Правила
Табличная
Аргумент – линейная функция (k=3).
F
(
x
)
?
функция
Используем таблицу и третье правило.
1
1
F ( x ) ( cos( 3 x )) cos( 3 x )
3
3
1
1
Проверка: F ( x ) cos( 3 x ) cos( 3 x )
3
3
1
1
( sin( 3 x ))( 3 x ) sin( 3 x ) 3 sin( 3 x )
3
3
f ( x ) F ( x ) первообразная для f ( x ) Формулы и правила
08.05.2020
дифференцирования

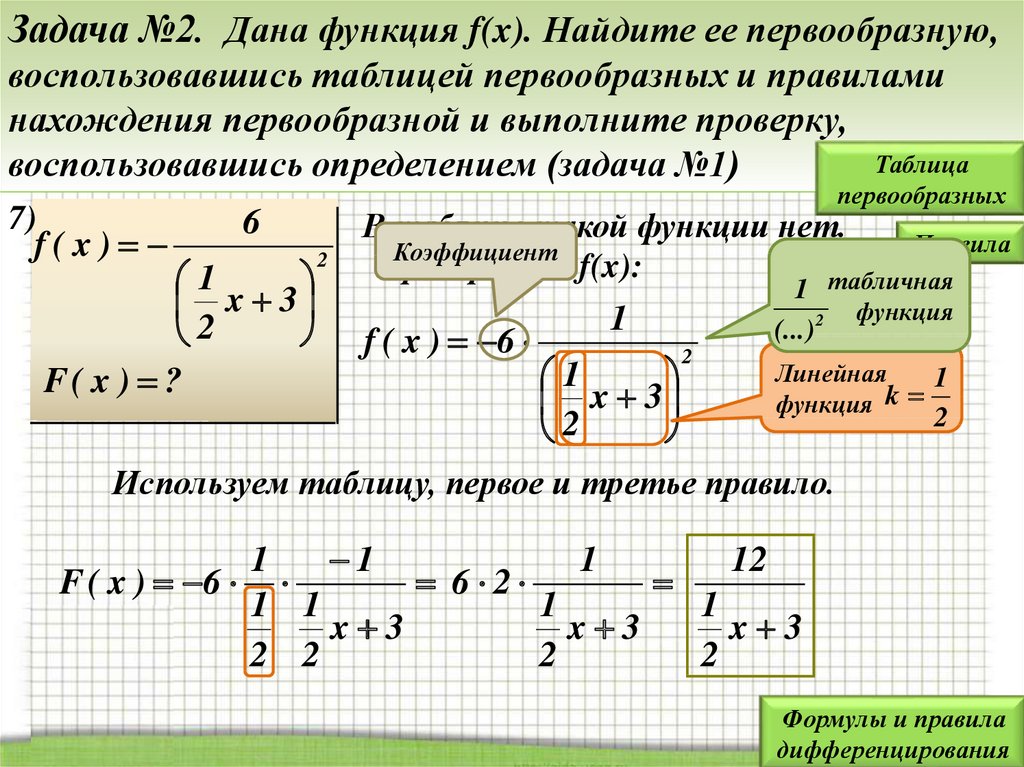
17.

Задача №2. Дана функция f(x). Найдите ее первообразную,
воспользовавшись таблицей первообразных и правилами
нахождения первообразной и выполните проверку,
Таблица
воспользовавшись определением (задача №1)
7)
f(x)
первообразных
6
1
x
3
2
F( x ) ?
2
В таблице такой функции нет.
Правила
Коэффициент
Преобразуем f(x):
табличная
f ( x ) 6
1
(...) 2
1
1
x
3
2
2
функция
Линейная
1
k
функция
2
Используем таблицу, первое и третье правило.
1
1
1
12
F ( x ) 6
6 2
1 1
1
1
x 3
x 3
x 3
2 2
2
2
Формулы и правила
дифференцирования

18.

Задача №2. Дана функция f(x). Найдите ее первообразную,
воспользовавшись таблицей первообразных и правилами
нахождения первообразной и выполните проверку,
Таблица
воспользовавшись определением (задача №1)
7)
f(x)
6
1
x
3
2
F( x ) ?
2
F( x )
первообразных
12
Правила
1
x 3
2
1
Проверка: F ( x ) 12
1 x 3
2
6
1
1
1
1
f(x)
12
x 3 12
2
2
2
1
1
2
1
2
x
3
x
3
x
3
2
2
2
F ( x ) первообразная
для
f( x)
Формулы и правила
дифференцирования

19.

Задача №2. Дана функция f(x). Найдите ее первообразную,
воспользовавшись таблицей первообразных и правилами
нахождения первообразной и выполните проверку,
Таблица
воспользовавшись определением (задача №1)
8)
первообразных
В таблице такой функции нет.
Коэффициент
Преобразуем f(x):
1
f(x)
4 9 0 ,25 x
F( x ) ?
1
1
f(x)
4 9 0 ,25 x
Правила
1 табличная
функция
...
Линейная
функция k 0 ,25
Используем первое и третье правило.
1
1
1
F( x )
2 9 0 ,25 x ( 4 ) 2 9 0 ,25 x
4
4 0 ,25
2 9 0 ,25 x
Формулы и правила
дифференцирования

20.

Задача №2. Дана функция f(x). Найдите ее первообразную,
воспользовавшись таблицей первообразных и правилами
нахождения первообразной и выполните проверку,
Таблица
воспользовавшись определением (задача №1)
8)
первообразных
Правила
1
f(x)
4 9 0 ,25 x
F ( x ) 2 9 0 ,25 x
F( x ) ?
Проверка: F ( x ) ( 2 9 0 ,25 x )
1
2( 9 0 ,25 x ) 2
( 9 0 ,25 x )
2 9 0 ,25 x
1
( 0 ,25 )
9 0 ,25 x
1
1
1
f(x)
9 0 ,25 x 4 4 9 0 ,25 x
F ( x ) первообразная
для
f( x)
Формулы и правила
дифференцирования

21.

Задача №2. Дана функция f(x). Найдите ее первообразную,
воспользовавшись таблицей первообразных и правилами
нахождения первообразной и выполните проверку,
Таблица
воспользовавшись определением (задача №1)
первообразных
9) f ( x ) 2 sin x 2 cos x В таблице таких функций
Табличная
нет. Преобразуем f(x):
функция
F( x ) ?
2
2
Правила
f ( x ) 2(sin2 x cos 2 x ) 2 1
Коэффициент
Используем таблицу и второе правило: F ( x ) 2 x 2 x
Проверка:
F ( x ) ( 2 x ) 2 2 1 2(sin2 x cos 2 x )
2 sin2 x 2 cos 2 x f ( x )
F ( x ) первообразная
08.05.2020
для
f( x)
Формулы и правила
дифференцирования

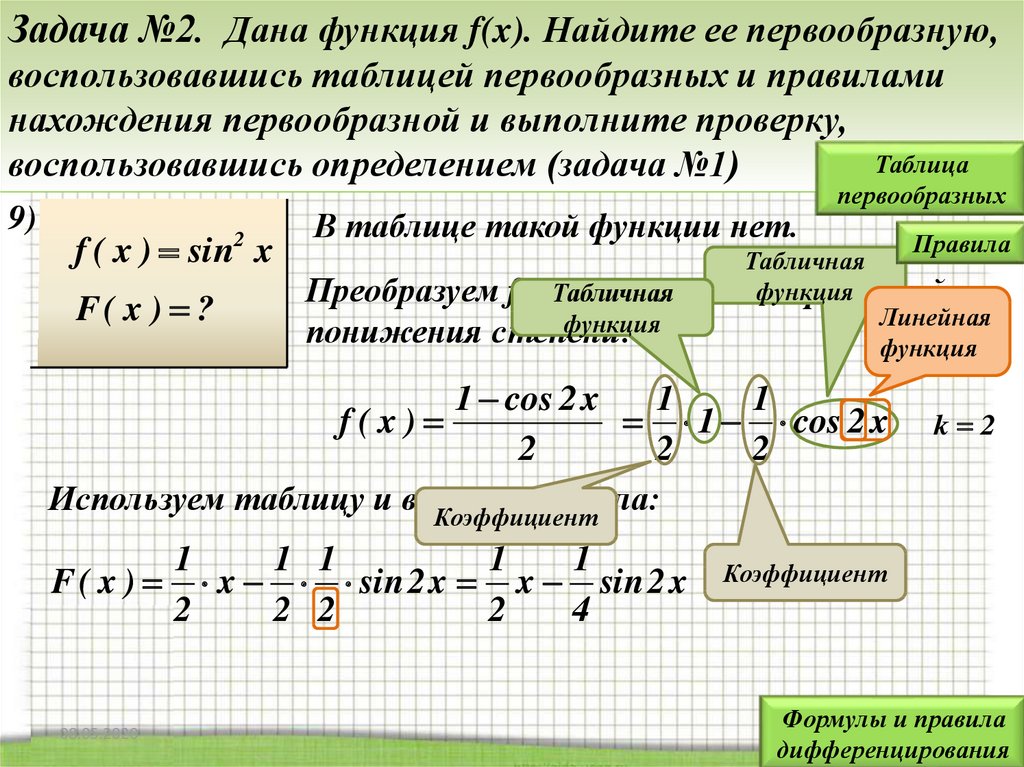
22.

Задача №2. Дана функция f(x). Найдите ее первообразную,
воспользовавшись таблицей первообразных и правилами
нахождения первообразной и выполните проверку,
Таблица
воспользовавшись определением (задача №1)
9)
f ( x ) sin x
2
F( x ) ?
В таблице такой функции нет.
первообразных
Правила
Табличная
функция
Преобразуем f(x),Табличная
воспользуемся
формулой
Линейная
функция
понижения степени:
функция
1 cos 2 x
1
1
f(x)
1 cos 2 x
2
2
2
Используем таблицу и всеКоэффициент
три правила:
1
1 1
1
1
F ( x ) x sin 2 x x sin 2 x
2
2 2
2
4
08.05.2020
k 2
Коэффициент
Формулы и правила
дифференцирования

23.

Задача №2. Дана функция f(x). Найдите ее первообразную,
воспользовавшись таблицей первообразных и правилами
нахождения первообразной и выполните проверку,
Таблица
воспользовавшись определением (задача №1)
9)
первообразных
1
1
f ( x ) sin x F ( x ) x sin 2 x
2
4
F( x ) ?
Правила
2
1
1
Проверка: F ( x ) x sin 2 x
4
2
1 1
1 1
1 1
cos 2 x ( 2 x ) cos 2 x 2 cos 2 x
2 4
2 4
2 2
1 cos 2 x
2
sin x f ( x )
2
F ( x ) первообразная для f ( x )
08.05.2020
Формулы и правила
дифференцирования

24.

самостоятельно найти общий вид
первообразных данных функций
1) f(x) = x2 – cosx;
2) f(x) = -3;
3) f(x) = 10 sinx;
4) f(x) = -2sin4x;
5) f(x) = 5x4 + x2 ;
6) f(x) = (3x – 1)2;
08.05.2020
27