Похожие презентации:
Электрические цепи переменного тока
1.
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКАВ электротехнике переменный ток применяется более широко, чем
постоянный. Это связано с возможностью легко преобразовать его для передачи
на расстояние и потребления в народном хозяйстве.
Переменным током называют ток, который изменяется во времени по
величине и направлению. Чаще всего переменный ток в электротехнике может
быть однофазным и трёхфазным.
Переменный однофазный синусоидальный ток
В
технике
широко
используются
процессы,
изменяющиеся
по
периодическому закону. Однофазный синусоидальный ток представляет
собой переменный ток, изменяющийся во времени по периодическому,
синусоидальному закону (который, также, называют гармоническим законом).
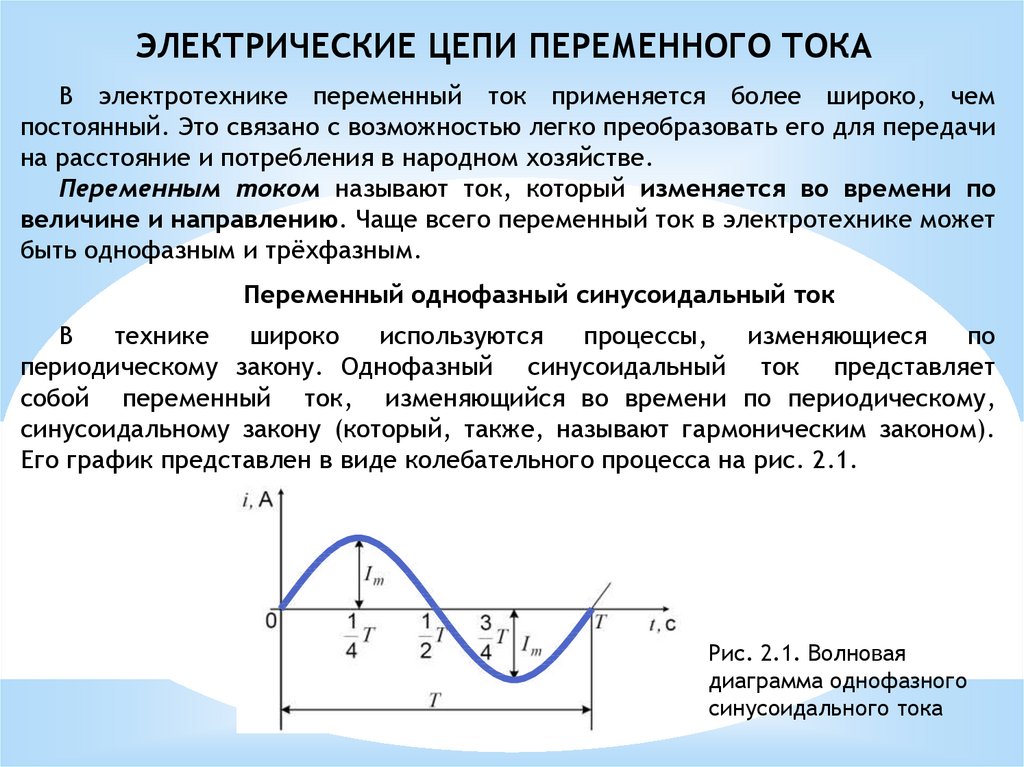
Его график представлен в виде колебательного процесса на рис. 2.1.
Рис. 2.1. Волновая
диаграмма однофазного
синусоидального тока
2.
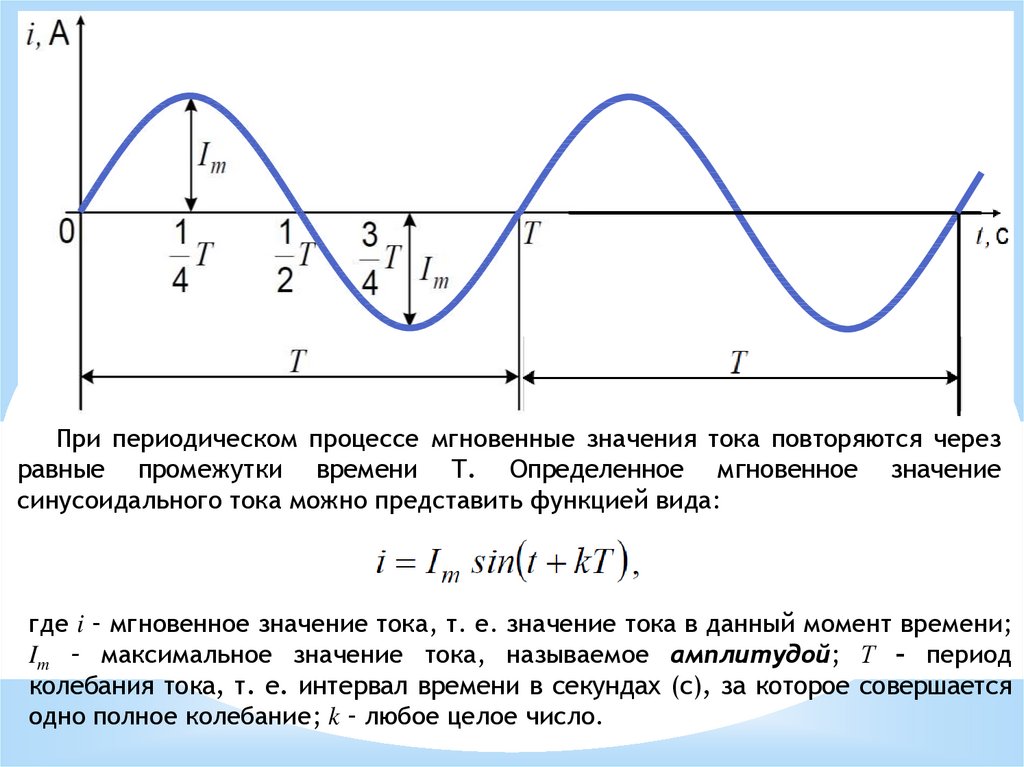
При периодическом процессе мгновенные значения тока повторяются черезравные промежутки времени Т. Определенное мгновенное значение
синусоидального тока можно представить функцией вида:
где i – мгновенное значение тока, т. е. значение тока в данный момент времени;
Im – максимальное значение тока, называемое амплитудой; Т – период
колебания тока, т. е. интервал времени в секундах (с), за которое совершается
одно полное колебание; k – любое целое число.
3.
ЧастотаНа основе понятия периода Т вводится понятие частоты f :
Частота – это число периодов колебаний какого либо процесса (тока,
напряжения и др.) за одну секунду. Измеряется в герцах (Гц), 1 Гц = 1/с.
Угловая (круговая) частота
В теории электротехники ось времени (ось аргумента) часто представляют
не в секундах (единица времени), а в углах. Для их измерения используют
безразмерную радианную величину.
При этом вводится понятие круговой (угловой, циклической) частоты w,
рад/с, равной числу периодов колебания тока (напряжения) за 2p секунд:
4.
В результате введения понятия круговой частоты ω график синусоидальноготока в виде волновой диаграммы (см. рис. 2.2) можно изобразить через
радианное измерение аргумента.
Рис. 2.2. График синусоидального тока в
виде волновой диаграммы
В этом случае
функцией вида:
закон
изменения синусоидального
для рис. 2.2-а
для рис. 2.2-б
тока выражается
5.
Анализируя выражения представленных на рис. 2.2 функций, вводимпонятия:
1) фаза (аргумент) – величина (wt + y). Фаза характеризует состояние
колебания, т. е. она даёт возможность определить численное значение
изменяющейся величины в данный момент времени t;
2) значение фазы при t = 0, когда wt + y = w*0 + y = y, называется
начальной фазой и обозначается y.
При радианном измерении аргумента синуса wt в течение времени Т фаза
тока увеличивается на 2p.
Круговая частота w показывает, на сколько радиан изменится фаза тока за
1 секунду.
6.
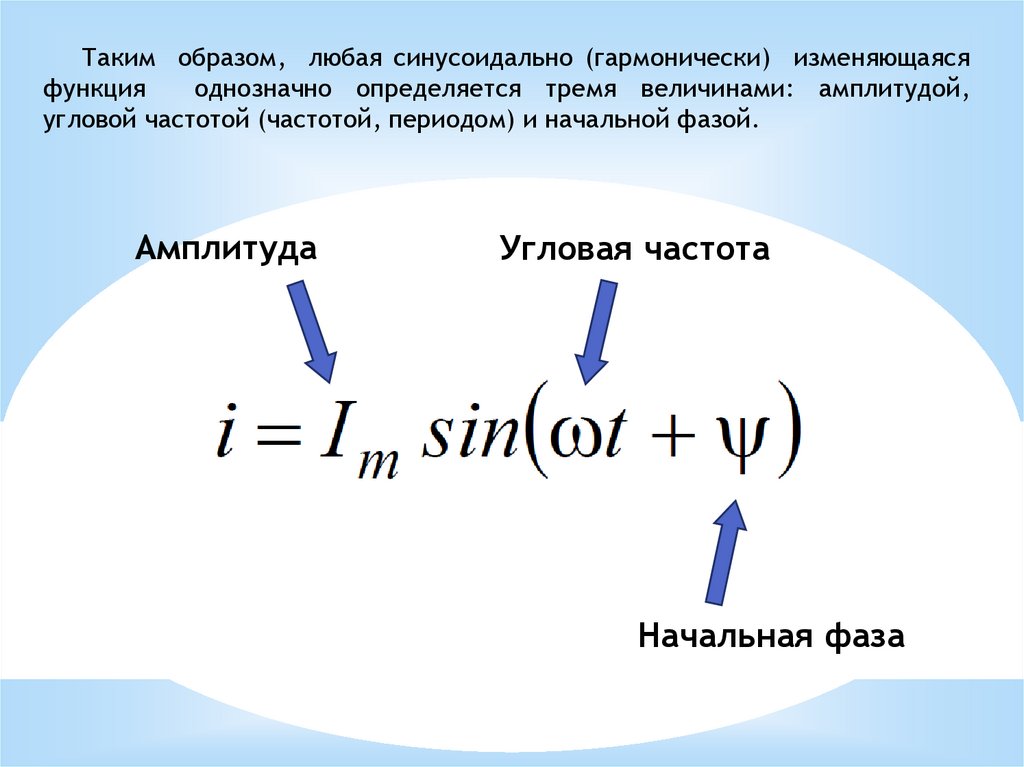
Таким образом, любая синусоидально (гармонически) изменяющаясяфункция
однозначно определяется тремя величинами: амплитудой,
угловой частотой (частотой, периодом) и начальной фазой.
Амплитуда
Угловая частота
Начальная фаза
7.
ХАРАКТЕРИСТИКИ СИНУСОИДАЛЬНЫХ ВЕЛИЧИНДействующее значение синусоидально изменяющейся
величины переменного тока и напряжения
Кроме понятий мгновенного и максимального значений тока и напряжения,
существует понятие их действующего значения.
Например, действующее значение I синусоидального тока i = Imsin(wt)
численно равно значению такого постоянного тока, который за время, равное
периоду синусоидального тока, выделяет на сопротивлении R такое же
количество теплоты, что и синусоидальный ток.
Действующее
значение
тока
ещё
называют
эффективным
или
среднеквадратичным. Его определяют из выражения:
Аналогично определяют действующее значение напряжения:
8.
Среднее значение синусоидально изменяющейсявеличины переменного тока и напряжения
Под средним значением синусоидального переменного тока понимают его
среднее значение за полпериода, и определяют из выражения:
Аналогично определяется среднее значение переменного напряжения:
9.
Коэффициенты амплитуды и формыКоэффициент амплитуды представляет собой отношение амплитуды
периодически изменяющейся функции к её действующему значению.
Так, для синусоидального тока:
Коэффициент формы – это отношение действующего значения
периодически изменяющейся функции к её среднему значению за полпериода.
Так, для синусоидального тока:
Коэффициенты амплитуды Ka и формы Kф для несинусоидальных
периодических токов и напряжений будут не равны своим значениям для
синусоидальной функции.
Отличие Ka от 1,41 и Kф от 1,11 позволяет судить о том, насколько
несинусоидальный ток или напряжение отличается (искажается) от
синусоидального.
10.
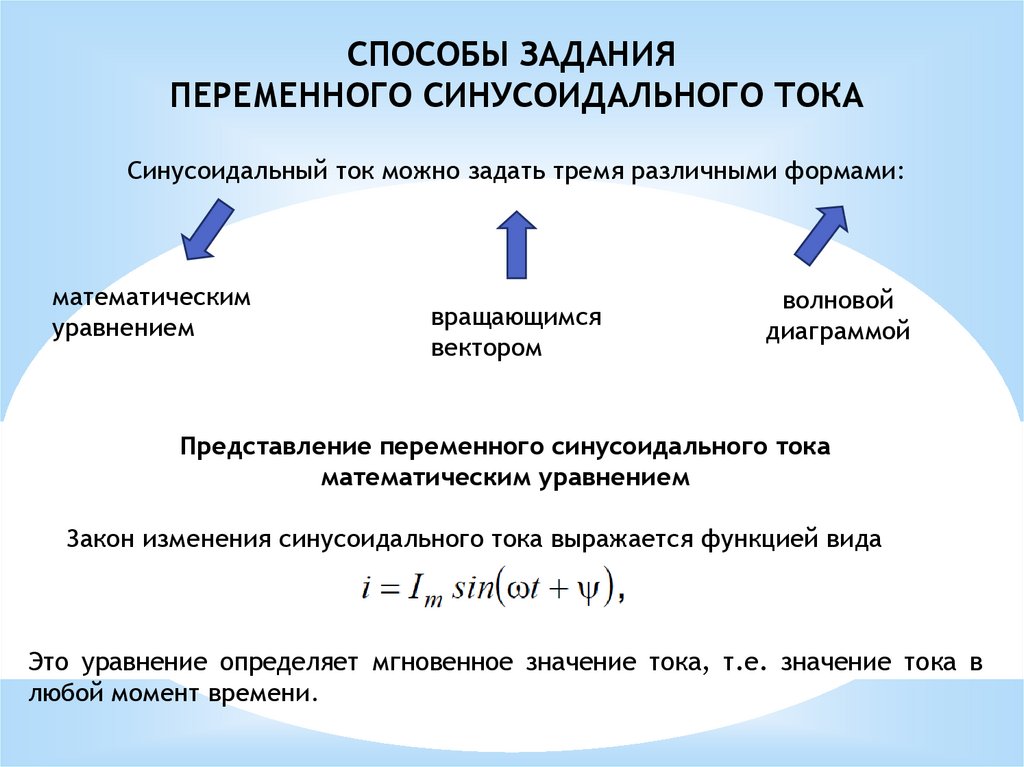
СПОСОБЫ ЗАДАНИЯПЕРЕМЕННОГО СИНУСОИДАЛЬНОГО ТОКА
Синусоидальный ток можно задать тремя различными формами:
математическим
уравнением
вращающимся
вектором
волновой
диаграммой
Представление переменного синусоидального тока
математическим уравнением
Закон изменения синусоидального тока выражается функцией вида
Это уравнение определяет мгновенное значение тока, т.е. значение тока в
любой момент времени.
11.
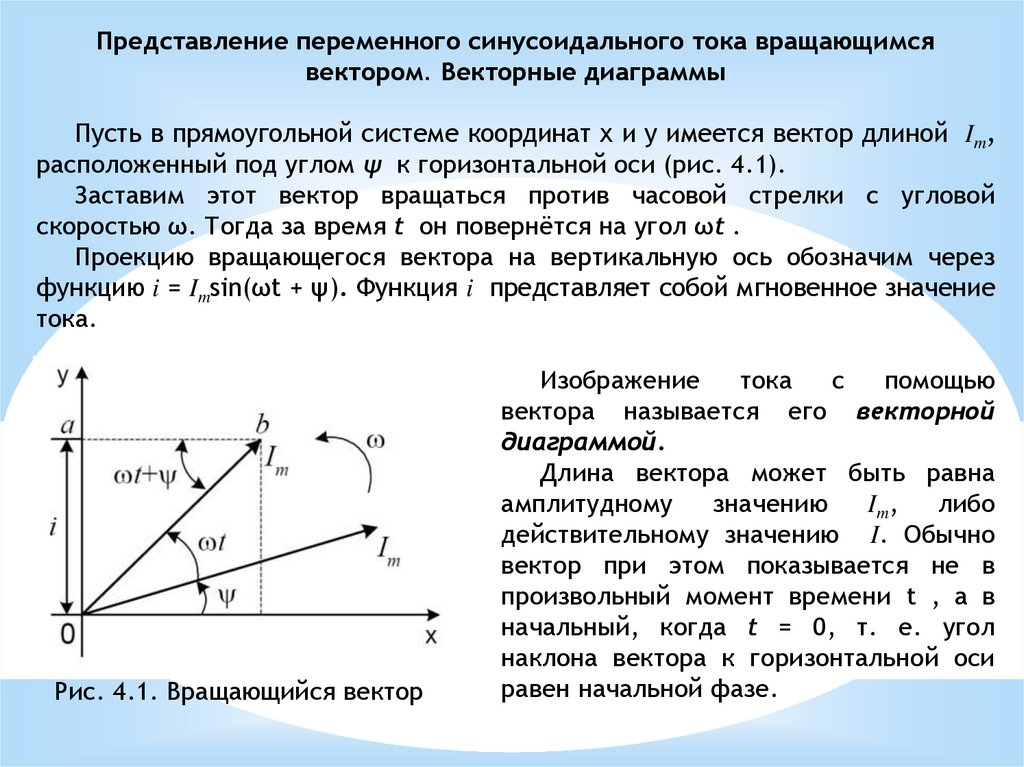
Представление переменного синусоидального тока вращающимсявектором. Векторные диаграммы
Пусть в прямоугольной системе координат х и у имеется вектор длиной Im,
расположенный под углом ψ к горизонтальной оси (рис. 4.1).
Заставим этот вектор вращаться против часовой стрелки с угловой
скоростью ω. Тогда за время t он повернётся на угол ωt .
Проекцию вращающегося вектора на вертикальную ось обозначим через
функцию i = Imsin(ωt + ψ). Функция i представляет собой мгновенное значение
тока.
Рис. 4.1. Вращающийся вектор
Изображение
тока
с
помощью
вектора называется его векторной
диаграммой.
Длина вектора может быть равна
амплитудному
значению
Im,
либо
действительному значению I. Обычно
вектор при этом показывается не в
произвольный момент времени t , а в
начальный, когда t = 0, т. е. угол
наклона вектора к горизонтальной оси
равен начальной фазе.
12.
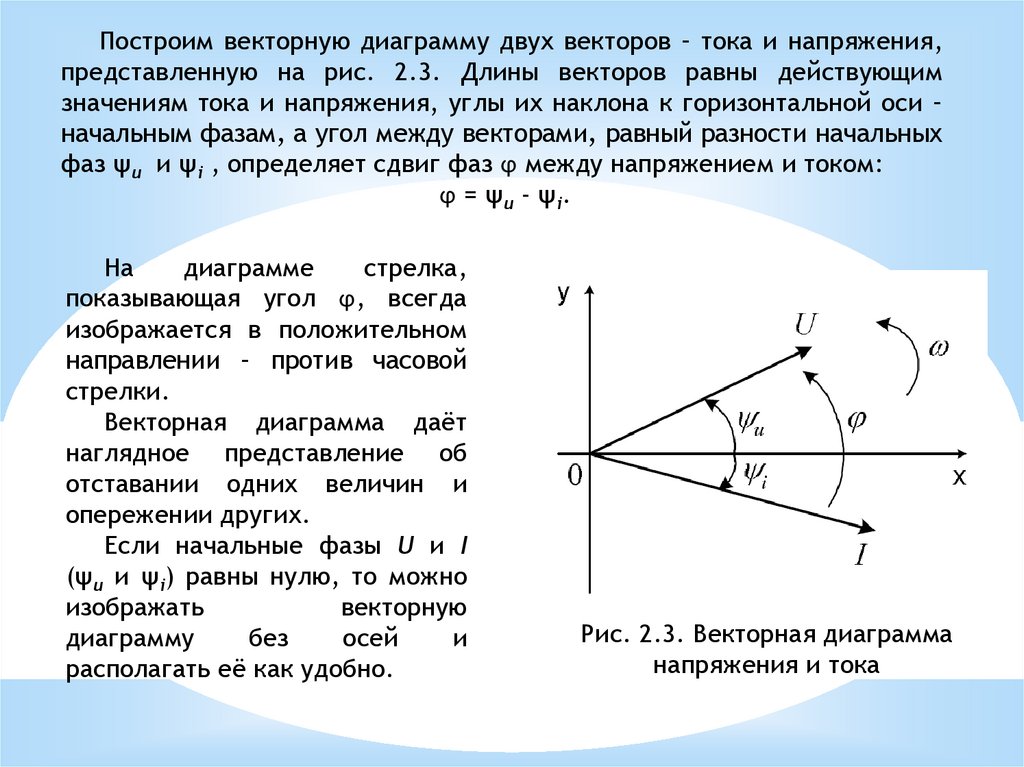
Построим векторную диаграмму двух векторов – тока и напряжения,представленную на рис. 2.3. Длины векторов равны действующим
значениям тока и напряжения, углы их наклона к горизонтальной оси –
начальным фазам, а угол между векторами, равный разности начальных
фаз ψu и ψi , определяет сдвиг фаз ϕ между напряжением и током:
ϕ = ψ u - ψi .
На
диаграмме
стрелка,
показывающая угол ϕ, всегда
изображается в положительном
направлении – против часовой
стрелки.
Векторная диаграмма даёт
наглядное представление об
отставании одних величин и
опережении других.
Если начальные фазы U и I
(ψu и ψi) равны нулю, то можно
изображать
векторную
диаграмму
без
осей
и
располагать её как удобно.
Рис. 2.3. Векторная диаграмма
напряжения и тока
13.
Представление переменного синусоидального токаволновой диаграммой
График синусоидального тока можно изобразить в виде волновой
диаграммы, представленный на рис. 2.4.
На волновой диаграмме указана начальная фаза, которая определяется
углом ψ, измеряемым от ближайшей к началу координат точки перехода
синусоиды через ноль до точки начала координат. Начальная фаза ψ
положительна в тех случаях, когда начало синусоиды смещено от точки ноль
(начало координат) влево и наоборот – отрицательна, когда смещена вправо.
Рис. 2.4. Волновая диаграмма синусоидального тока
14.
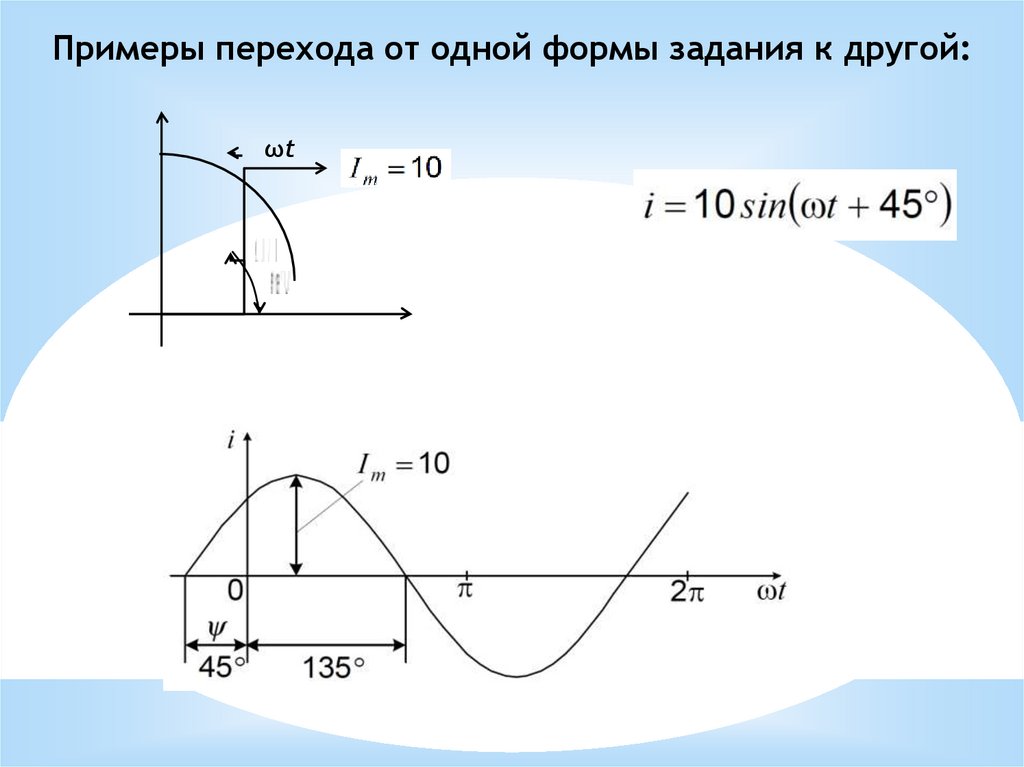
Примеры перехода от одной формы задания к другой:ωt
15.
ЗАКОНЫ КИРХГОФА В ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКАИ МЕТОДЫ РАСЧЁТА ЭТИХ ЦЕПЕЙ
Для мгновенных значений ЭДС, токов и напряжений остаются
справедливыми сформулированные ранее законы Кирхгофа.
Первый закон Кирхгофа: в любой момент времени алгебраическая
сумма токов в узле электрической цепи равна нулю
(4.1)
где n – число ветвей, сходящихся в узле.
Второй закон Кирхгофа: в любой момент времени в замкнутом контуре
электрической цепи алгебраическая сумма ЭДС равна алгебраической
сумме напряжений на всех остальных элементах контура
(4.2)
где m – число ветвей, образующих контур.
16.
(4.1)(4.2)
Токи, напряжения и ЭДС, входящие в уравнения (4.1) и (4.2), есть
синусоидальные функции времени, которые рассматриваются как проекции
определённых векторов на оси координат.
Так как сложению проекций соответствует сложение векторов и
соответствующих им комплексных чисел, то справедливыми будут
следующие уравнения, которые можно записать как для действующих, так и
для амплитудных значений. Законы Кирхгофа в векторной форме:
(4.3)
Следовательно,
возможны
два
способа
расчёта
цепей
синусоидального тока:
- выполнение операций непосредственно над синусоидальными
функциями времени по уравнениям (4.1) и (4.2)
- применение метода векторных диаграмм, основанного на
уравнениях (4.3).
17.
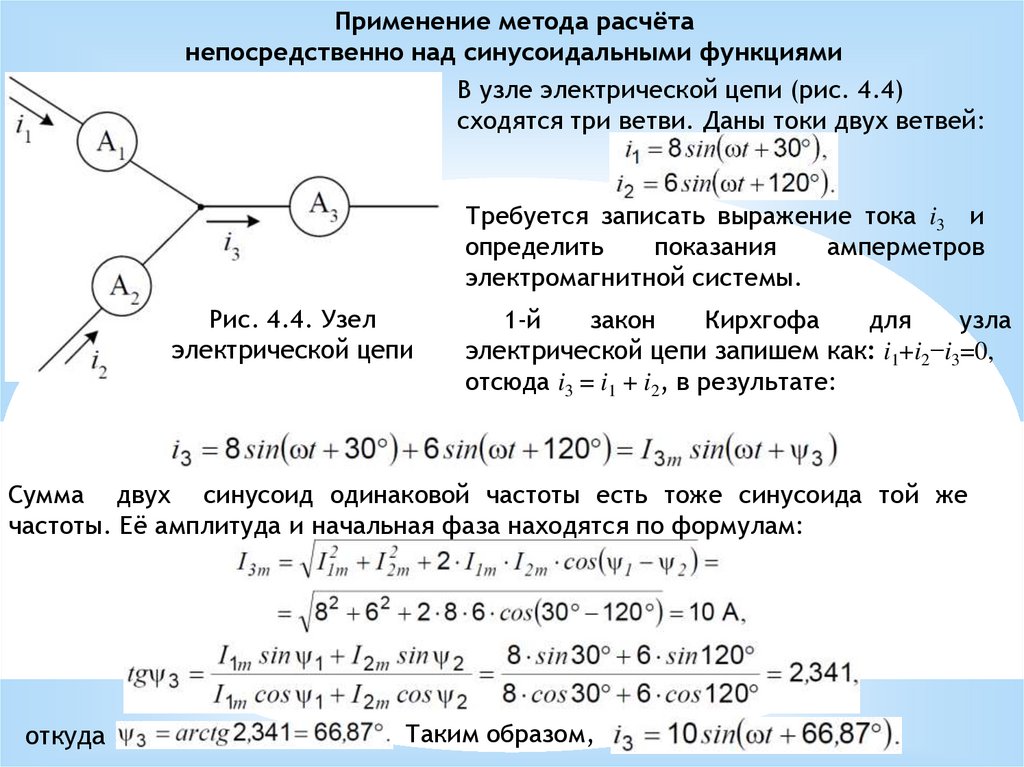
Применение метода расчётанепосредственно над синусоидальными функциями
В узле электрической цепи (рис. 4.4)
сходятся три ветви. Даны токи двух ветвей:
Требуется записать выражение тока i3 и
определить
показания
амперметров
электромагнитной системы.
Рис. 4.4. Узел
электрической цепи
1-й
закон
Кирхгофа
для
узла
электрической цепи запишем как: i1+i2−i3=0,
отсюда i3 = i1 + i2, в результате:
Сумма двух синусоид одинаковой частоты есть тоже синусоида той же
частоты. Её амплитуда и начальная фаза находятся по формулам:
откуда
Таким образом,
18.
Применение метода расчёта с помощью векторных диаграммНа примере, в соответствии с 1-м законом
Кирхгофа в векторной форме для цепи (рис.
4.4), запишем:
Построим в прямоугольной системе координат
сумму векторов
(рис. 4.5). Необходимо
определить
.
Рис. 4.5. Векторная
диаграмма токов
Начальная фаза ψ3 тока
горизонтальной оси
Так как треугольник oab – прямоугольный, а
сторона ab равна длине вектора
, то в этом
треугольнике:
равна углу наклона вектора
к
19.
Определяем показания аргументов. Известно, что приборы электромагнитнойсистемы показывают действующие значения токов и напряжений. Поэтому
Проанализировав численные значения токов I1, I2 и I3, обращаем внимание
на то, что
Это не ошибка. Надо знать, что в цепях синусоидального тока для
показаний приборов законы Кирхгофа не справедливы.
В итоге можно складывать только мгновенные значения токов
(синусоидальные функции времени) и векторы. Однако складывать
численные значения токов и напряжений, а также показания приборов
нельзя.
20.
Выводы:1.
Метод расчёта непосредственно над синусоидальными функциями
практически не применяется из-за громоздкости вычислительных
операций с синусоидами.
2. Метод векторных диаграмм наиболее удобен при решении сложных
задач.












 Физика
Физика








