Дифракционные решетки и линзы. Лекция 8

1.

Лекция 8
Дифракционные решетки и линзы
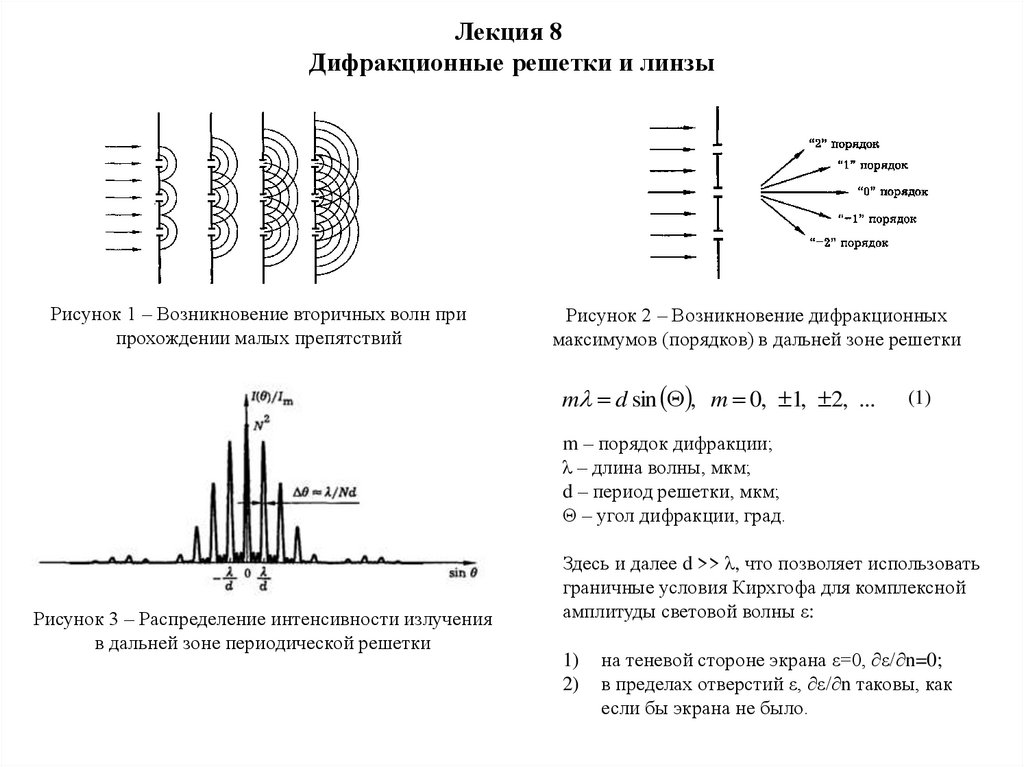
Рисунок 1 – Возникновение вторичных волн при
прохождении малых препятствий
Рисунок 2 – Возникновение дифракционных
максимумов (порядков) в дальней зоне решетки
m d sin , m 0, 1, 2, ...
(1)
m – порядок дифракции;
λ – длина волны, мкм;
d – период решетки, мкм;
Θ – угол дифракции, град.
Рисунок 3 – Распределение интенсивности излучения
в дальней зоне периодической решетки
Здесь и далее d >> λ, что позволяет использовать
граничные условия Кирхгофа для комплексной
амплитуды световой волны ε:
1)
2)
на теневой стороне экрана ε=0, ∂ε/∂n=0;
в пределах отверстий ε, ∂ε/∂n таковы, как
если бы экрана не было.

2.

Лекция 8
Дифракционные решетки и линзы
zд r 2 /
z r 2 /
Рисунок 4 – Ближняя и дальняя зоны дифракции
для дифракционного отверстия (pinhole)
Рисунок 5 – Геометрическая постановка
задачи дифракции Френеля
(2)
(3)
дифракционный интеграл Гюйгенса - Френеля
ρ - длина вектора, соединяющего точку на дифракционной
решетке с точкой наблюдения в плоскости изображения
ε(x0, y0, z) – распределение комплексной амплитуды поля в плоскости наблюдения;
ε0(x, y, z=0) – распределение комплексной амплитуды поля в плоскости дифракционной структуры;
z – расстояние между дифракционной структурой и плоскостью наблюдения, м;
λ – длина волны, м; k = 2π/λ – волновой вектор, рад/м.

3.

Лекция 8
Дифракционные решетки и линзы
Приближение Френеля - дифракция слаборасходящихся (параксиальных) пучков
(4)
(5)
Приближение Френеля исключает из рассмотрения области прилежащие к дифракционной структуре, а
также периферийные участки в плоскости наблюдения, что следует из выражения (4). Использование
формулы (5) подразумевает замену вторичных точечных источников сферической формы вторичными
источниками параболической формы.
Подставив (5) в (2) и пренебрегая отличием ρ от z в знаменателе, получим:
(6)
Пусть распределение поля в плоскости решетки зависит только от одной координаты, что означает
одномерную дифракционную структуру:
(7)
В случае равномерного освещения для одномерной дифракционной структуры формула (6) упрощается:
(8)
x0,i , z
1 I Ikz M
Ik
e
0 x j exp
x j x0,i 2 , M D / x
2 z
2z
j 1
интеграл Гюйгенса - Френеля

4.

Лекция 8
Дифракционные решетки и линзы
Опыты по дифракции лазерных пучков показывают, что в дальней зоне угловое распределение
интенсивности перестает зависеть от координаты z, отсчитываемой вдоль оси пучка. Картина дифракции
приобретает устойчивую структуру, вид которой зависит только от распределения поля в начальном
сечении. Этот случай относят к дифракции Фраунгофера – дифракции в дальней зоне.
Рисунок 6 – Геометрическая постановка
задачи дифракции Фраунгофера
(9)
ε(x, y) – распределение поля в сечении решетки z=0;
λ – длина волны, м; k = 2π/λ – волновой вектор, рад/м.
(10)
x, y – координаты в плоскости решетки, м;
x0, y0 – координаты в плоскости наблюдения, м.
(11)
(12)

5.

Лекция 8
Дифракционные решетки и линзы
(13)
Отличие заключается в замене радиус – вектора ρ на расстояние b, связывающее центр решетки с точкой
наблюдения. Это налагает ограничения на поперечный размер дальней зоны, в которой отличие ρ и b
может быть существенным.
Подставив (13) в (9) и пренебрегая отличием ρ от b в знаменателе, получим:
(14)
Для одномерных дифракционных решеток формула (14) преобразуется к виду:
(15)
в зависимости от поперечной
координаты x0
(16)
в зависимости от угла
наблюдения (дифракции)
(17)
где d – начальный поперечный размер пучка, м; zд – дифракционная длина пучка, м.
При выполнении условия (17) устанавливается стабильное угловое распределение интенсивности, не
изменяющееся при дальнейшем распространении:
(18)

6.

Лекция 8
Дифракционные решетки и линзы
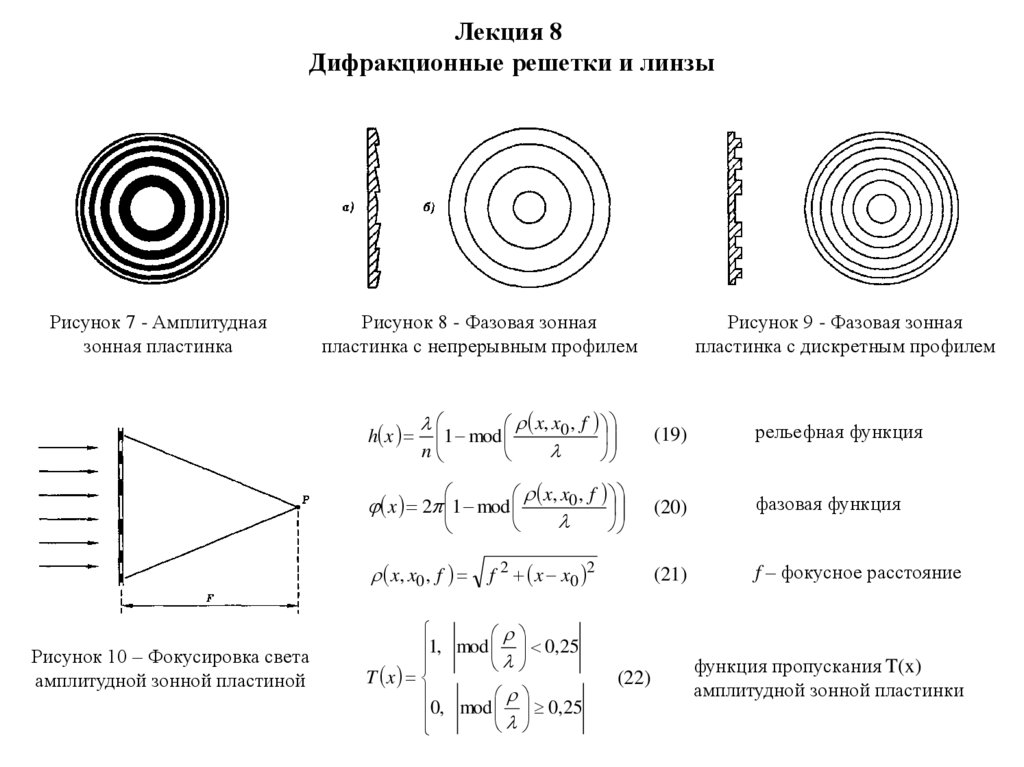
Рисунок 7 - Амплитудная
зонная пластинка
h x
x, x0 , f
1 mod
n
(19)
рельефная функция
x 2 1 mod
(20)
фазовая функция
x, x0 , f
(21)
f – фокусное расстояние
Рисунок 10 – Фокусировка света
амплитудной зонной пластиной
Рисунок 9 - Фазовая зонная
пластинка с дискретным профилем
Рисунок 8 - Фазовая зонная
пластинка с непрерывным профилем
x, x0 , f
f 2 x x0 2
1, mod 0,25
T x
0, mod 0,25
(22)
функция пропускания T(x)
амплитудной зонной пластинки

7.

Лекция 8
Дифракционные решетки и линзы
Рисунок 11 – Непрерывный фазовый профиль
Рисунок 12 – 5-уровненый фазовый профиль
Рисунок 13 – 3-уровненый фазовый профиль
Рисунок 14 – 1-уровненый фазовый профиль

8.

Лекция 8
Дифракционные решетки и линзы
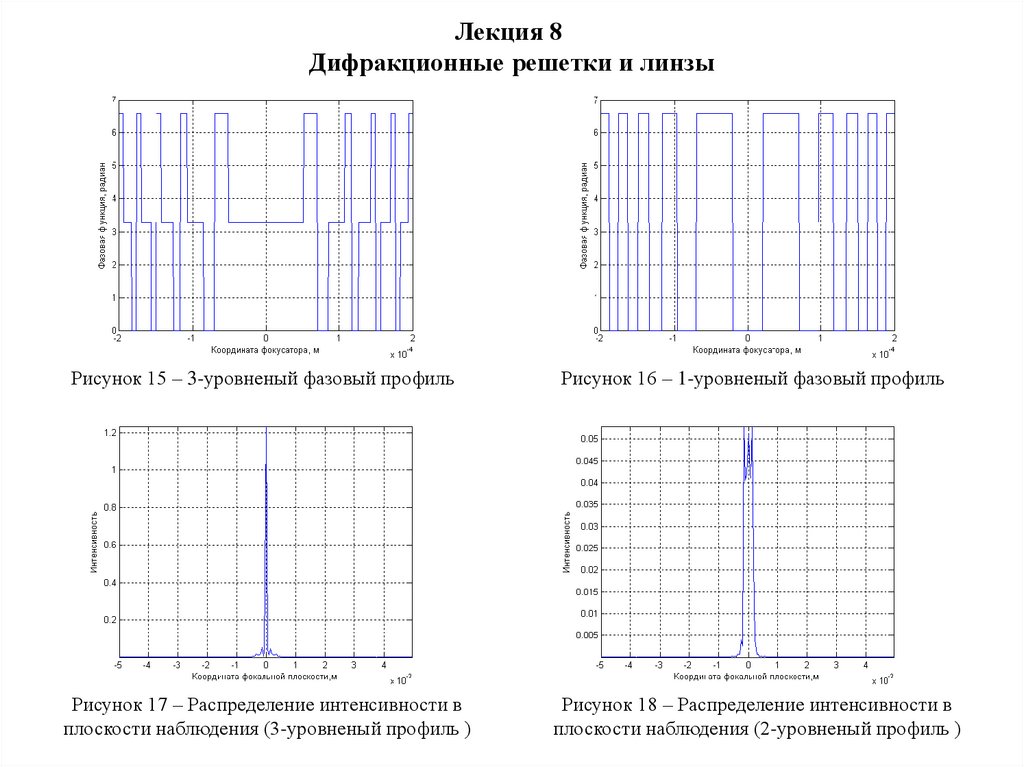
Рисунок 15 – 3-уровненый фазовый профиль
Рисунок 16 – 1-уровненый фазовый профиль
Рисунок 17 – Распределение интенсивности в
плоскости наблюдения (3-уровненый профиль )
Рисунок 18 – Распределение интенсивности в
плоскости наблюдения (2-уровненый профиль )

9.

Лекция 8
Дифракционные решетки и линзы
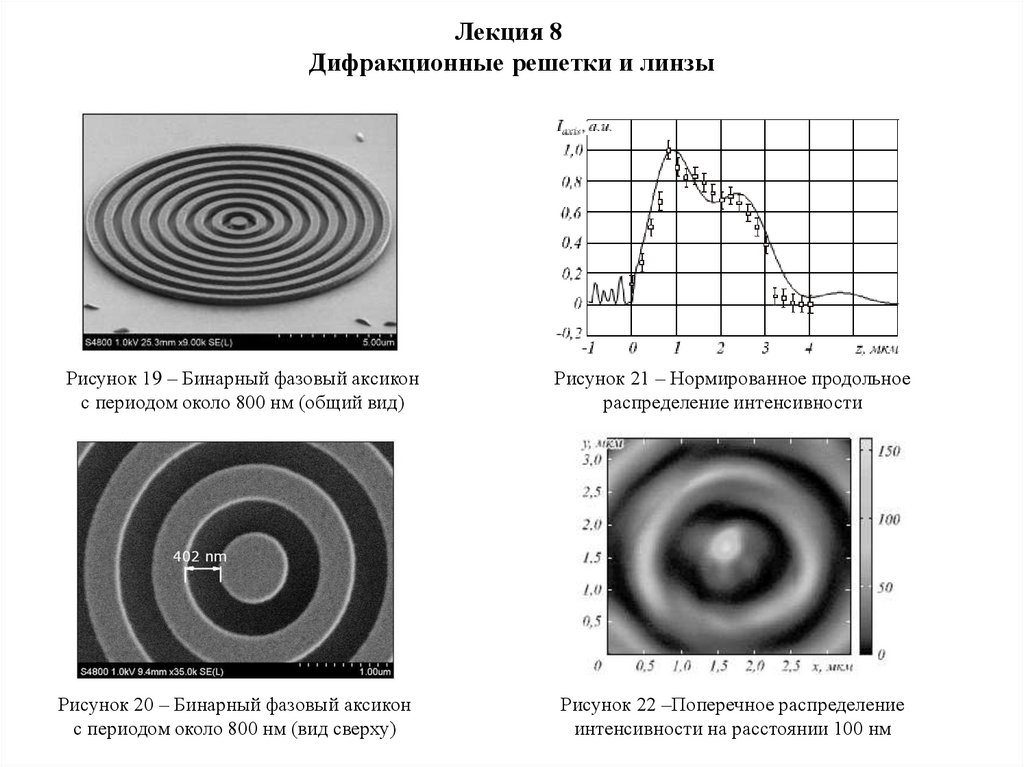
Рисунок 19 – Бинарный фазовый аксикон
с периодом около 800 нм (общий вид)
Рисунок 20 – Бинарный фазовый аксикон
с периодом около 800 нм (вид сверху)
Рисунок 21 – Нормированное продольное
распределение интенсивности
Рисунок 22 –Поперечное распределение
интенсивности на расстоянии 100 нм

10.

Лекция 8
Дифракционные решетки и линзы
Рисунок 25 – Схема эксперимента по
исследованию фазовых зонных пластин для
рентгеновского диапазона
Рисунок 23 – Фазовая зонная пластина
(вид сверху)
Рисунок 24 – Фазовая зонная пластина
(профилограмма)
Рисунок 26 – Измеренное распределение
интенсивности 4-х фазовых пластин

11.

Лекция 8
Дифракционные решетки и линзы
Практическое применение дифракционных решеток и линз:
1) дисперсионные элементов (спектральные фильтров) в спектрометрах и монохроматорах лабораторного,
промышленного, мобильного, авиационного, космического назначения;
2) поворотные зеркала и элементы обратной связи лазерных резонаторов и параметрических генераторов,
3) корректирующие элементы дифракционно - рефракционных объективов, применяемые для уменьшения
влияния прямой дисперсии материала линз;
4) делители пучка с заданным отношением интенсивности, применяемые от УФ до ТГц диапазона;
5) цветоделительные элементы (решетки), обеспечивающие пространственное разделение и фокусировку
излучения выделяемых спектральных диапазонов;
6) фокусаторы лазерного излучения различных диапазонов, в т.ч. инфракрасного излучения мощных
промышленных лазеров с P ~ 1 – 10 кВт для лазерной пайки, наплавки, сварки, гравировки, резки;
7) формирователи лазерных пучков специальной формы для решения уникальных задач:
- оптический захват и перемещение микрочастиц,
- передача сил и моментов на микромеханические элементы (лопасти, турбины, актуаторы),
- устойчивая передача данных по атмосферной линии связи при воздействии турбулентности,
запыленности, тумана, дождя, снега и т.д.

12.

Лекция 8
Дифракционные решетки и линзы
Список использованных источников (дифракционные решетки и линзы):
1) Ахманов, С.А. Физическая оптика: учебник, 2-е изд. [Текст] / С.А.Ахманов, С.Ю.Никитин. – М: изд-во
МГУ, 2004. – 656 с.
2) Ландсберг, Г.С. Оптика: учеб. пособие для вузов, 6-е изд. [Текст] / Г.С.Лансберг. - М: Физматлит,
2003. – 848 с.
3) Сивухин, Д.В. Общий курс физики. Т4. Оптика [Текст] / Д.В.Сивухин. - М: Наука, 1980. – 752 с.
4) Гудмен, Дж. Введение в Фурье-оптику: пер. с англ. [Текст] / Дж.Гудмен. – М: Мир, 1970. – 364 с.
5) Методы компьютерной оптики: 2-е изд. / под. ред. В.А.Сойфера [Текст] / М: Физматлит, 2003. – 688 с.
6) Дифракционная компьютерная оптика / под. ред. В.А.Сойфера [Текст] / М: Физматлит, 2011. – 736 с.
7) Дифракционная нанофотоника / под. ред. В.А.Сойфера [Текст] / А.В.Гаврилов, Д.Л.Головашкин,
Л.Л.Досколович и др. – М: Физматлит, 2011. – 680 с.
8) Журнал «Компьютерная оптика».
9) Журнал «Квантовая электроника».

13.

Лекция 8
Управляемые дифракционные решетки
Рисунок 1 – Основные виды дифракционных
решеток: а) амплитудная пропускающая, б)
фазовая пропускающая, в) амплитудная
отражающая, г) фазовая отражающая
Рисунок 3 – Возникновение дифракционных
порядков (максимумов диаграммы
направленности) в дальней зоне решетки
Рисунок 2 – Возникновение вторичных волн при
прохождении малых препятствий
Рисунок 4 – Распределение интенсивности
излучения в дальней зоне решетки

14.

Лекция 8
Управляемые дифракционные решетки
Рисунок 5 – Конструкция фазовой
управляемой дифракционной решетки:
1 – электрооптический кристалл;
2 – электроды;
3 – защитное покрытие;
4 – картинная плоскость;
5 – падающее излучение;
6 – дифракционные порядки в дальней зоне
nd 2
h1
2
d
n
I z1 ~
z12
z11
(1)
(2)
A z
h1 – глубина проникновения электрического поля, м;
d – период электродов, м;
n – показатель преломления кристалла LiNbO3;
λ – длина волны, м.
Расчет электрического поля показал, что h1 ≤ d
exp jkr z , z1
r z , z1
2
cos n , r exp j e z exp j пад z dz
(3)
где z, z1 – координата плоскости электродов и картинной плоскости; z11, z12 – пределы освещенной области
электродов; r – расстояние между z, z1; φпад(z) – фазовое пропускание при отсутствии напряжения, радиан.
A z A z 0 t1t 2 t эл exp h
(4)
t1, t2 – пропускание границы кристалл-воздух;
tэл – пропускание периодических электродов;
h – толщина кристалла, м;
α – коэффициент линейного поглощения, м-1.

15.

Лекция 8
Управляемые дифракционные решетки
Запишем tэл для электродов шириной b с межэлектродным зазором a. Полагая центр решетки
совмещенным с центром координатной оси z, а расположение электродов – периодичным, для
пропускания справедливо:
t эл t O t C t P
tO
o max
z b(o 1) 2 a 2o 1 z bo 2 a 2o 1
1
1
o 1
p max
1
1
z bp a 2 p 1 z b( p 1) a 2 p 1
tP
2
2
p 1
(5)
1
1
tC z a z a
2
2
x
2u
х 2
z
2u
z 2
0
(6)
ne z , x
1
ne3r33 E z z , x
2
1 ne2 r33 E z z , x
e z
3
ne r33 E z z , x dx (8)
h
ne
(7)
e i
3
ne r33 E z zi , x j dx j
j
(9)
где u=u(z,x) – электрический потенциал, В; εz, εx - относительные диэлектрические проницаемости, равный
24,5 и 83 для х-среза ниобата лития; ne=2,2 – необыкновенный показатель преломления; r33=30,9 м/В –
электрооптический коэффициент; h – толщина кристалла, м; λ – длина волны излучения, м; Ez(z,x) –
напряженность электрического поля вдоль полярной оси z ниобата лития, В/м.

16.

Лекция 8
Управляемые дифракционные решетки
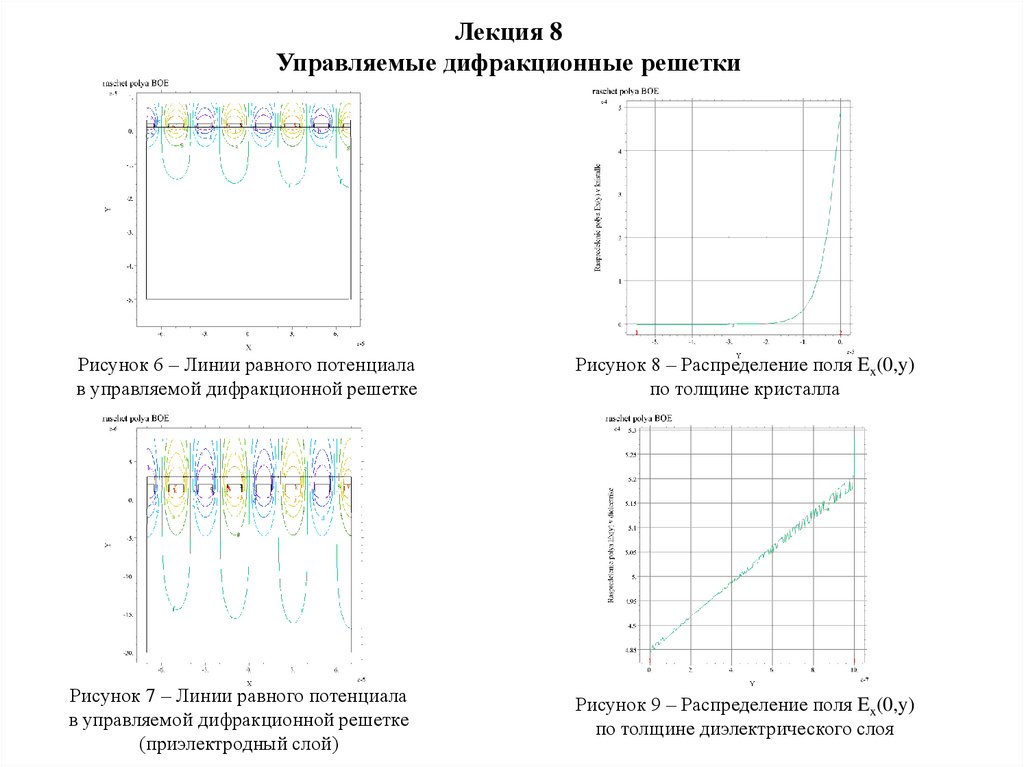
Рисунок 6 – Линии равного потенциала
в управляемой дифракционной решетке
Рисунок 7 – Линии равного потенциала
в управляемой дифракционной решетке
(приэлектродный слой)
Рисунок 8 – Распределение поля Ex(0,y)
по толщине кристалла
Рисунок 9 – Распределение поля Ex(0,y)
по толщине диэлектрического слоя

17.

Лекция 8
Управляемые дифракционные решетки
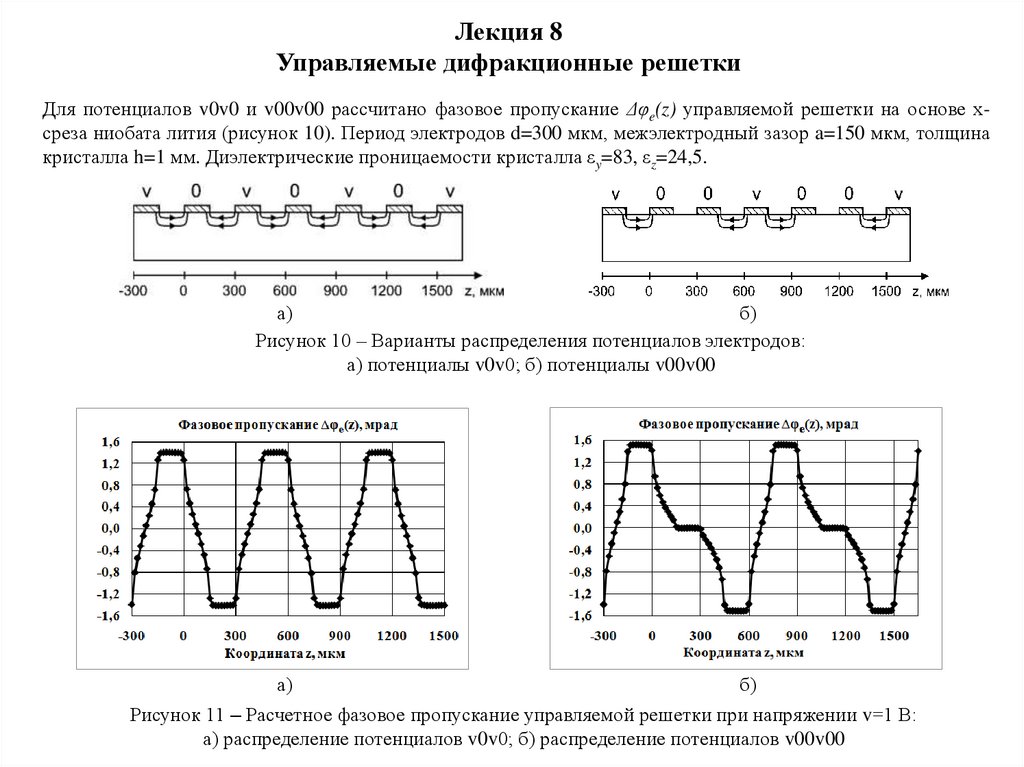
Для потенциалов v0v0 и v00v00 рассчитано фазовое пропускание Δφe(z) управляемой решетки на основе хсреза ниобата лития (рисунок 10). Период электродов d=300 мкм, межэлектродный зазор a=150 мкм, толщина
кристалла h=1 мм. Диэлектрические проницаемости кристалла εy=83, εz=24,5.
а)
б)
Рисунок 10 – Варианты распределения потенциалов электродов:
а) потенциалы v0v0; б) потенциалы v00v00
а)
б)
Рисунок 11 – Расчетное фазовое пропускание управляемой решетки при напряжении v=1 В:
а) распределение потенциалов v0v0; б) распределение потенциалов v00v00

18.

Лекция 8
Управляемые дифракционные решетки
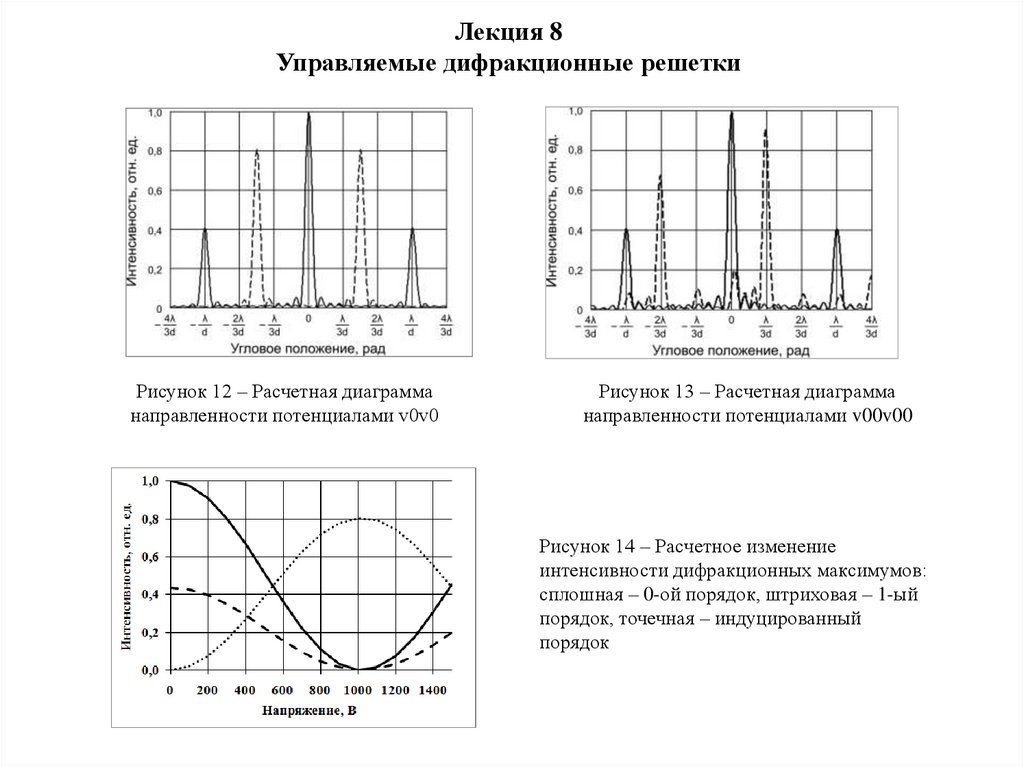
Рисунок 12 – Расчетная диаграмма
направленности потенциалами v0v0
Рисунок 13 – Расчетная диаграмма
направленности потенциалами v00v00
Рисунок 14 – Расчетное изменение
интенсивности дифракционных максимумов:
сплошная – 0-ой порядок, штриховая – 1-ый
порядок, точечная – индуцированный
порядок

19.

Лекция 8
Управляемые дифракционные решетки
Период электродов - 300±5 мкм, межэлектродный зазор - 175±5 мкм для образца с потенциалами v00v00.
Для управляемой решетки с потенциалами вида v0v0 период электродов составлял 300±5 мкм,
межэлектродный зазор - 140±5 мкм Структура электродов в обоих случаях включала адгезионный слой
хрома толщиной 10 нм и верхний слой меди толщиной 250 нм. Электроды покрывались прозрачным
акриловым лаком, обеспечивающим электрическую изоляцию. Фотография приведена на рисунке 15.
Рисунок 15 – Внешний вид управляемой решетки с потенциалами v00v00
Рисунок 16 – Схема установки для исследования фазового пропускания:
1 – нейтральный фильтр, 2 – пространственный фильтр и расширитель пучка, 3 –
поляризатор, 4 – управляемая решетка, 5 – объектив 10х, 6 - анализатор

20.

Лекция 8
Управляемые дифракционные решетки
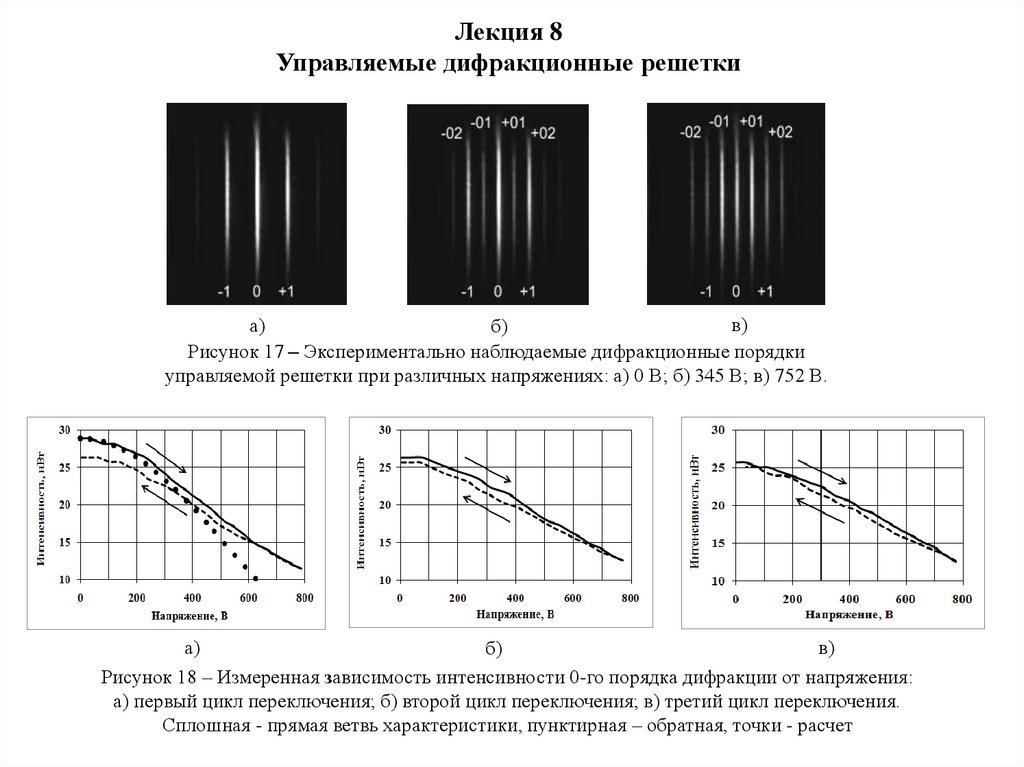
в)
а)
б)
Рисунок 17 – Экспериментально наблюдаемые дифракционные порядки
управляемой решетки при различных напряжениях: а) 0 В; б) 345 В; в) 752 В.
в)
а)
б)
Рисунок 18 – Измеренная зависимость интенсивности 0-го порядка дифракции от напряжения:
а) первый цикл переключения; б) второй цикл переключения; в) третий цикл переключения.
Сплошная - прямая ветвь характеристики, пунктирная – обратная, точки - расчет

21.

Лекция 8
Управляемые дифракционные решетки
а)
в)
б)
Рисунок 19 - Иглообразные оптические неоднородности в поверхностном слое кристалла
ниобата лития: а) между электродами; б) на краях электродов; в) сквозные
Оптические неоднородности имеют иглообразную форму, ориентированы перпендикулярно электродам
и примыкают к электродам с отрицательным потенциалом. Длина неоднородностей составляет до 100 мкм,
ширина – до 10 мкм. Вблизи краев электродов наблюдается увеличение размеров неоднородностей
(рисунок 19,б), обусловленное повышенной напряженностью электрического поля.
Влияние оптических неоднородностей (областей деполяризации кристалла LiNbO3):
1) поперечные размеры неоднородностей обуславливают рассеяние оптического излучения$
2) электрическое поле неоднородностей вызывает деполяризацию излучения и падение чувствительности
дифракционных порядков к управляющему электрическому напряжению;
3) проводимость области неоднородностей приводит к перераспределению электрического поля в
межэлектродном зазоре и уменьшению разности потенциалов между электродами. Это также снижает
чувствительность к управляющему электрическому напряжению.

22.

Лекция 8
Управляемые дифракционные решетки
а)
б)
в)
Рисунок 20 - Образование оптических неоднородностей:
а) напряжение 0 В; б) напряжение 686 В; в) напряжение 686 В с выдержкой 60 сек
а)
б)
Рисунок 21 – Фотографии электрических пробоев управляемой дифракционной решетки:
а) выгорание электрода вблизи места пробоя, б) выгорание электрода и контактной площадки

23.

Лекция 8
Управляемые дифракционные решетки
Список использованных источников (управляемые дифракционные решетки):
1) Паранин, В.Д. Экспериментальное исследование управляемых дифракционных решеток на основе
кристалла ниобата лития [Электронный ресурс] : дис. ... канд. физ.-мат. наук : 01.04.05 ; М-во
образования и науки Рос. Федерации, Самар. гос. аэрокосм. ун-т им. С. П. Королева (нац. исслед. ун-т)
(СГАУ). - Электрон. текстовые дан. (1 файл : 2,69 Мбайт). - 2014. http://www.ssau.ru/resources/dis_protection/Paranin/
2) Паранин, В.Д. Экспериментальное исследование управляемых дифракционных решеток на основе
кристалла ниобата лития [Электронный ресурс] : автореф. дис. ... канд. физ.-мат. наук : 01.04.05 ; М-во
образования и науки Рос. Федерации, Самар. гос. аэрокосм. ун-т им. С. П. Королева (нац. исслед. ун-т)
(СГАУ). - Электрон. текстовые дан. (1 файл : 2,69 Мбайт). - 2014. http://diss.ssau.ru/attachment.php?id=534
3) Паранин, В.Д. Методика исследования фазовой функции управляемых дифракционных
оптических элементов [Текст] / В.Д.Паранин, К.Н.Тукмаков // Квантовая электроника, 2014. - Т.44. № 4. - С. 371-375.
4) Паранин, В.Д. Исследование механизмов управления характеристиками дифракционной решетки,
выполненной на поверхности электрооптического кристалла ниобата лития [Текст] / В.Д.Паранин //
Журнал технической физики. - 2014. - Т.84. - Вып.11. - С.146-150.
5) Паранин, В.Д. Особенности формирования иглообразных доменов в поверхностном слое ниобата
лития Х-среза [Текст] / В.Д.Паранин // Журнал технической физики. - 2014. - Т.84. - Вып.12. - С.132-136.

24.

Благодарю за внимание