Геометрические (и физические) приложения двойных интегралов

1.

Справочный материал к практике 18 по
дисциплине «Математика» для студентов
направления подготовки
09.03.02 «Информационные системы и
технологии»
Геометрические (и физические) приложения двойных интегралов
Составитель:
ст. преподаватель кафедры «Физикоматематические науки» Черемухин А. Д.

2.

Таблица интегралов и примеры нахождения табличных интегралов от функций одной переменной
Примеры нахождения интегралов

3.

Нахождение площади фигуры
Площадь странной фигуры на плоскости – это всегда интеграл по области, образованной данной фигурой
Пример 1. Найдите площадь фигуры, образованно линиями
1. Надо нарисовать вообще эту фигуру
Разберемся с обозначениями. Слева область ограничивает прямая x = -5, снизу – сначала
прямая y = 0, потом прямая y = 2x-5, сверху – функция корня.
Основная сложность – переменная боковая и нижняя границы.
В случае, если верхние и нижние границы фигуры выражаются не одними и теми же
функциями, лучше всего разбивать фигуры на составляющие части
Также нам неизвестны левая и правая границы фигуры (ну с левой все ясно – прямая x =
-5 а правая – неизвестна).
Рассматриваем все поэтапно

4.

Нахождение площади фигуры
Площадь странной фигуры на плоскости – это всегда интеграл по области, образованной данной фигурой
Пример 1. Найдите площадь фигуры, образованной линиями
2. Найдем границы. Фигура заканчивается справа, там где линейная функция
пересекает функцию корня, откуда
Решим это уравнение
У нас осталась еще одна точка – там, где меняется функция, ограничивающая
фигуру снизу. Эта точка соответствует значению х, когда прямая пересекается с
осью абсцисс. Найдем это значение
То есть, до 5/2 наша фигура есть прямоугольная трапеция, а после – треугольник.
Искомая площадь есть сумма данных площадей

5.

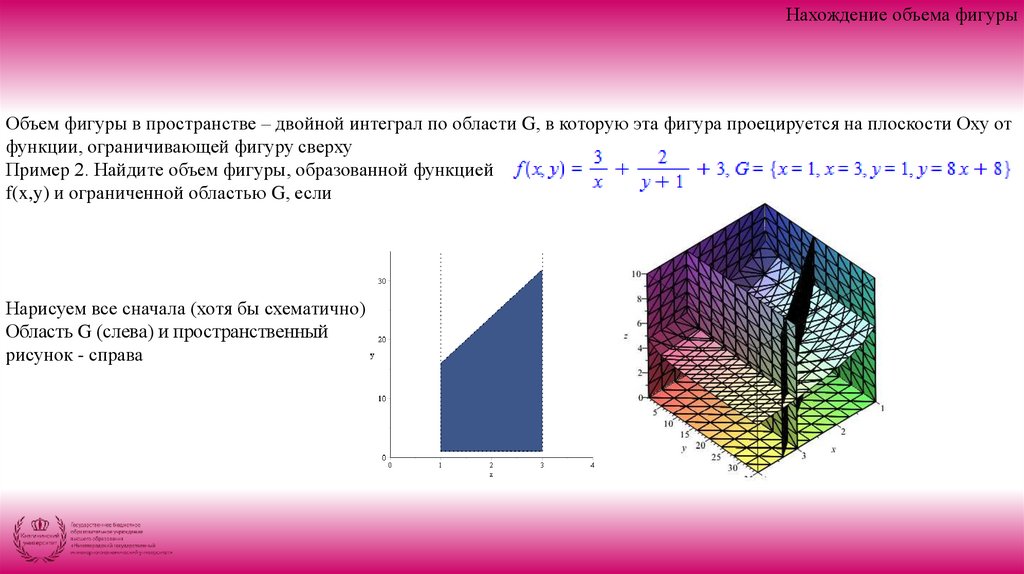
Нахождение объема фигуры
Объем фигуры в пространстве – двойной интеграл по области G, в которую эта фигура проецируется на плоскости Оху от
функции, ограничивающей фигуру сверху
Пример 2. Найдите объем фигуры, образованной функцией
f(x,y) и ограниченной областью G, если
Нарисуем все сначала (хотя бы схематично)
Область G (слева) и пространственный
рисунок - справа

6.

Нахождение объема фигуры
Объем фигуры в пространстве – двойной интеграл по области G, в которую эта фигура проецируется на плоскости Оху от
функции, ограничивающей фигуру сверху
Пример 2. Найдите объем фигуры, образованной функцией
f(x,y) и ограниченной областью G, если
Разберемся с областью G. Она проста, граница слева – x = 1, справа x = 3, снизу и сверху функции не меняются. Значит,
записываем

7.

Нахождение центра масс фигуры
Пример 3. Найдите центр масс плоской пластины формы G, если известна функция плотности ρ, если
Посмотрим на нашу пластину
Формулы. Координаты центра масс пластины находятся по формуле
Таким образом, порядок работы такой:
1. Определяем границы области G
2. Находим массу пластинки
3. Находим координаты центра масс
1. Границы области G – сверху и снизу функции не меняются, неизвестны левое
и правое значение. Их можно найти, приравняв уравнения верхней и нижней
границы

8.

Нахождение центра масс фигуры
Пример 3. Найдите центр масс плоской пластины формы G, если известна функция плотности ρ, если
Посмотрим на нашу пластину
2. Найдем массу пластинки

9.

Нахождение центра масс фигуры
Пример 3. Найдите центр масс плоской пластины формы G, если известна функция плотности ρ, если
Посмотрим на нашу пластину
3. По аналогии найдем остальные два интегралы и координаты