Похожие презентации:
Определение перемещений в плоских стержневых конструкциях
1. СТРОИТЕЛЬНАЯ МЕХАНИКА
Цель курса: Изучение методовстатического и динамического
расчетов инженерных сооружений
25.05.2020
ПГУ, лектор Турищев Л.С.
1
2.
Тема лекцииОПРЕДЕЛЕНИЕ
ПЕРЕМЕЩЕНИЙ В ПЛОСКИХ
СТЕРЖНЕВЫХ
КОНСТРУКЦИЯХ
25.05.2020
ПГУ, лектор Турищев Л.С.
2
3.
Цели лекции - напомнить:понятие деформации конструкции и ее
количественные характеристики
понятия полных, частичных и единичных
перемещений
определение перемещений от нагрузки
правило Верещагина
25.05.2020
ПГУ, лектор Турищев Л.С.
3
4. 1. Общие сведения о перемещениях
25.05.2020ПГУ, лектор Турищев Л.С.
4
5. Понятие деформации конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
5
6. Понятие деформации конструкции
Деформация конструкции изменение формы и размеровконструкции при приложении
внешних воздействий
25.05.2020
ПГУ, лектор Турищев Л.С.
6
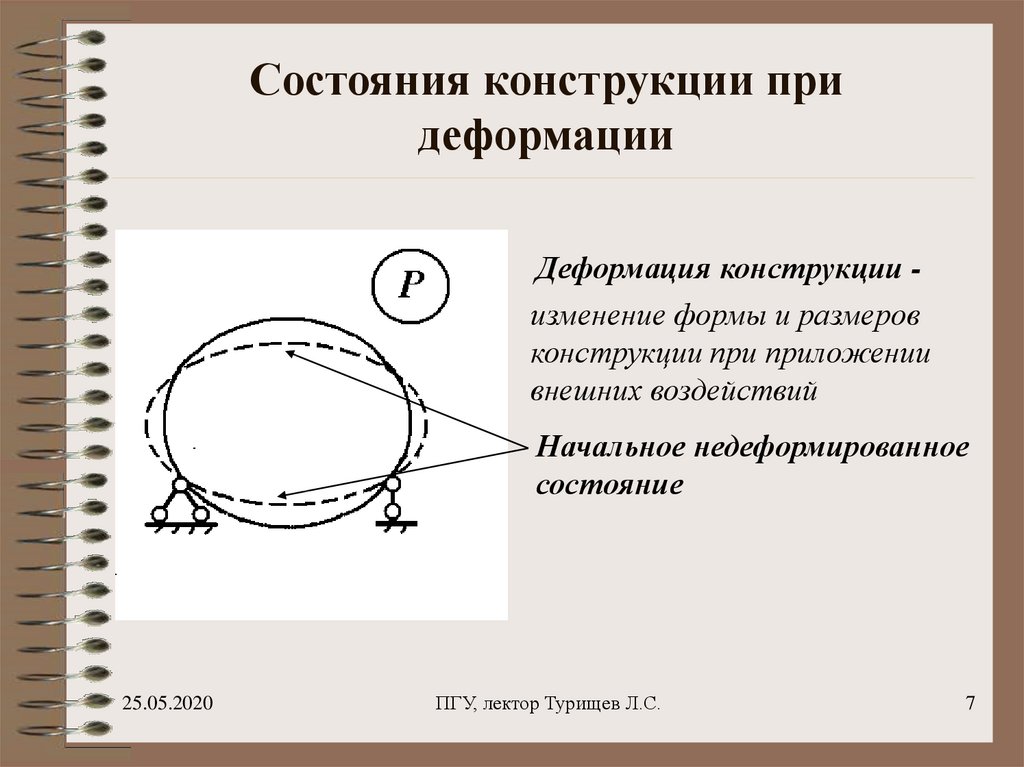
7. Состояния конструкции при деформации
Деформация конструкции изменение формы и размеровконструкции при приложении
внешних воздействий
Начальное недеформированное
состояние
25.05.2020
ПГУ, лектор Турищев Л.С.
7
8. Состояния конструкции при деформации
Деформация конструкции изменение формы и размеровконструкции при приложении
внешних воздействий
Начальное недеформированное
состояние
Конечное деформированное
состояние
25.05.2020
ПГУ, лектор Турищев Л.С.
8
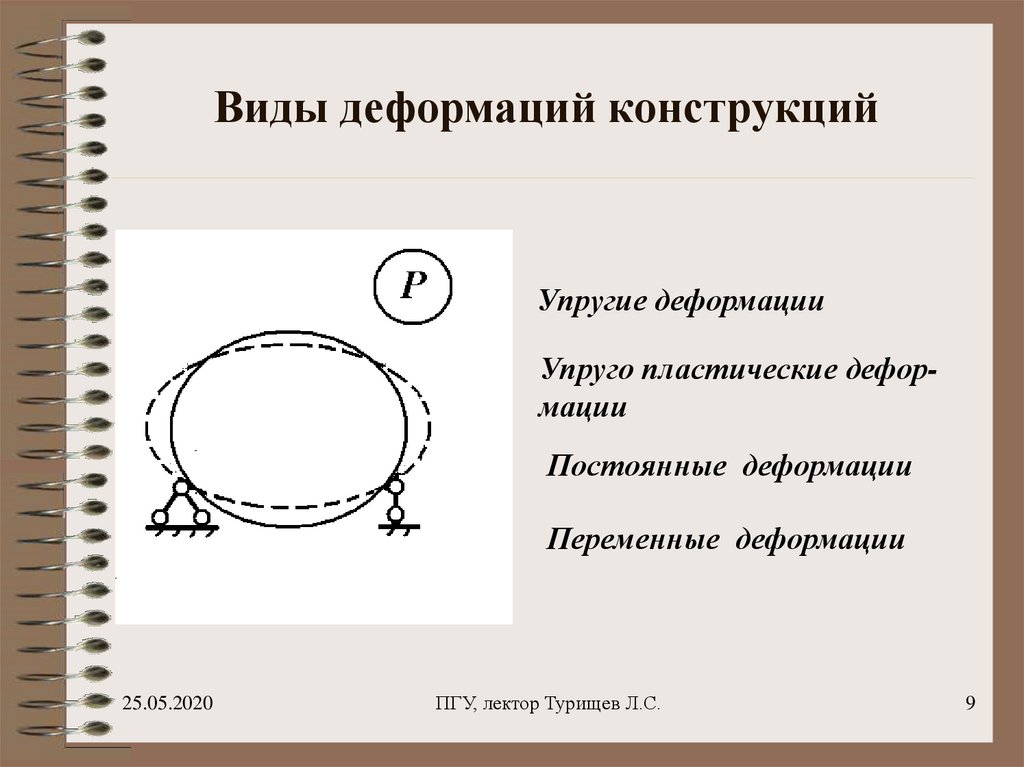
9. Виды деформаций конструкций
Упругие деформацииУпруго пластические деформации
Постоянные деформации
Переменные деформации
25.05.2020
ПГУ, лектор Турищев Л.С.
9
10. Виды деформаций конструкций, изучаемые в курсе
Упругие деформацииУпруго пластические деформации
Постоянные деформации
Переменные деформации
25.05.2020
ПГУ, лектор Турищев Л.С.
10
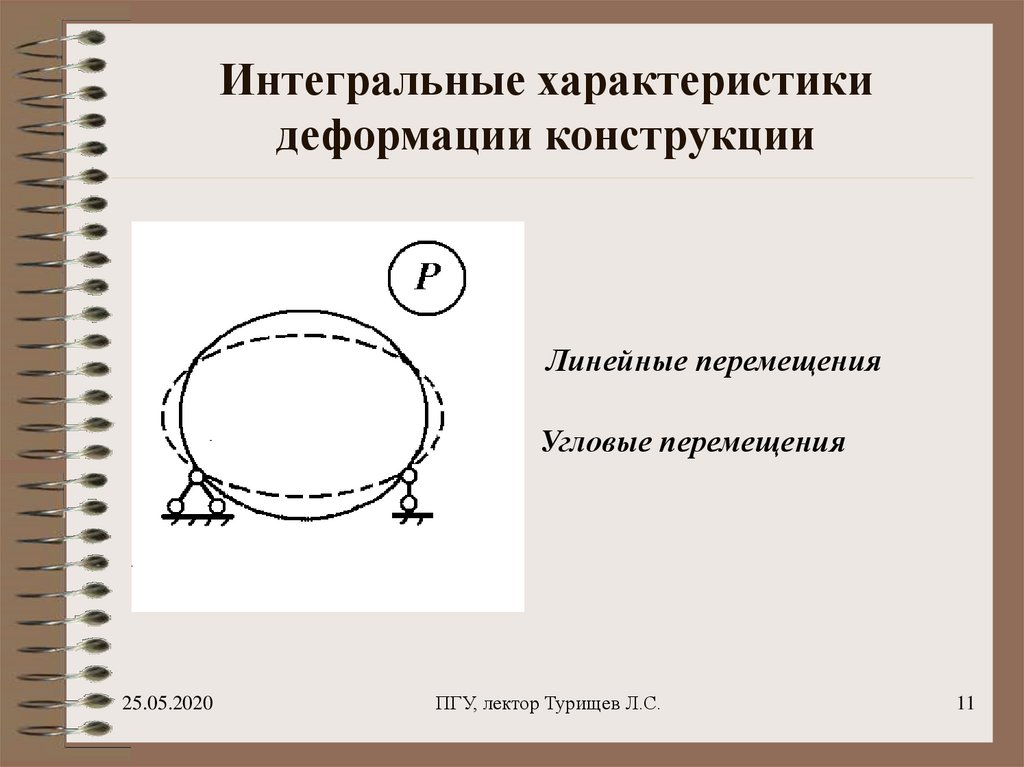
11. Интегральные характеристики деформации конструкции
Линейные перемещенияУгловые перемещения
25.05.2020
ПГУ, лектор Турищев Л.С.
11
12. Линейные перемещения конструкции
Перемещение характеризуется длиной отрезка, соединяющегоположение точки в начальном недеформированном состоянии
и конечном деформированном состоянии
25.05.2020
ПГУ, лектор Турищев Л.С.
12
13. Угловые перемещения конструкции
Перемещение характеризуется углом поворота отрезка прямой,соединяющего две произвольные точки конструкции при переходе из
начального недеформированного состояния в конечное
деформированное состояние
25.05.2020
ПГУ, лектор Турищев Л.С.
13
14. Цель определения перемещений конструкции
Пригодность конструкции кнормальной эксплуатации
характеризуется её жесткостью
и податливостью
25.05.2020
ПГУ, лектор Турищев Л.С.
14
15. Понятие жесткости и податливости конструкции
Жёсткость конструкции25.05.2020
ПГУ, лектор Турищев Л.С.
15
16. Понятие жесткости и податливости конструкции
Жёсткость конструкцииПодатливость конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
16
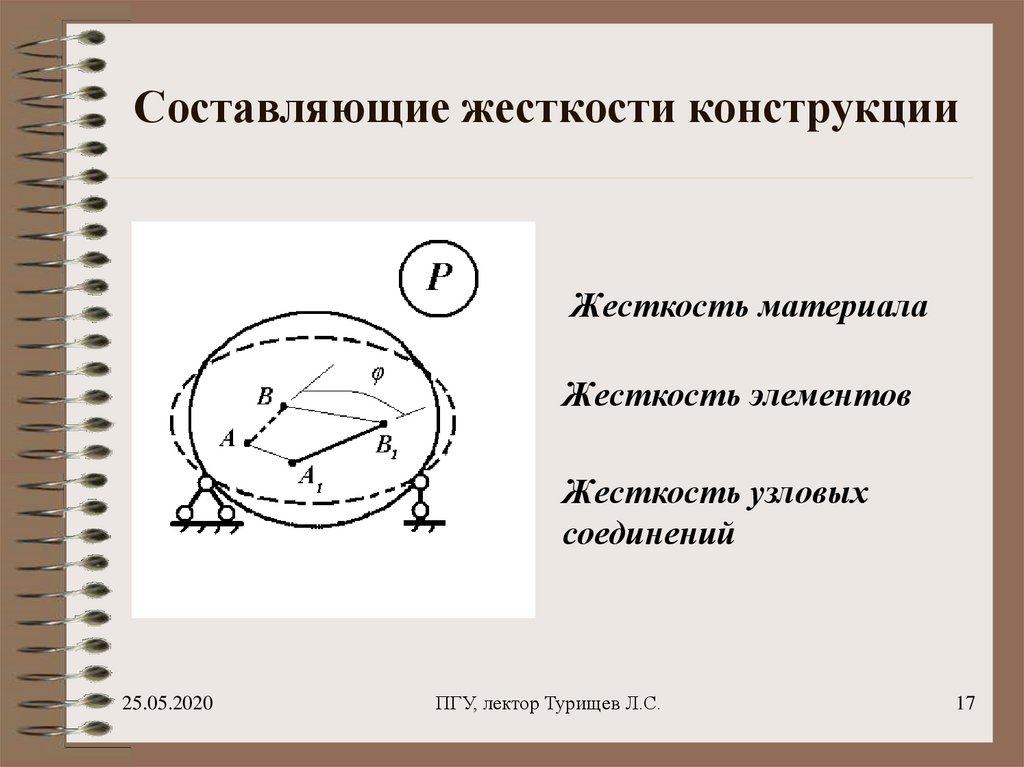
17. Составляющие жесткости конструкции
Жесткость материалаЖесткость элементов
Жесткость узловых
соединений
25.05.2020
ПГУ, лектор Турищев Л.С.
17
18. Жесткость материала конструкции
Характеризуется двумя модулямиупругости
E G
Модуль упругости Е характеризует
способность материала
сопротивляться возникновению упругих
линейных деформаций
Модуль сдвига G характеризует
способность материала сопротивляться
возникновению упругих сдвиговых
деформаций
25.05.2020
ПГУ, лектор Турищев Л.С.
18
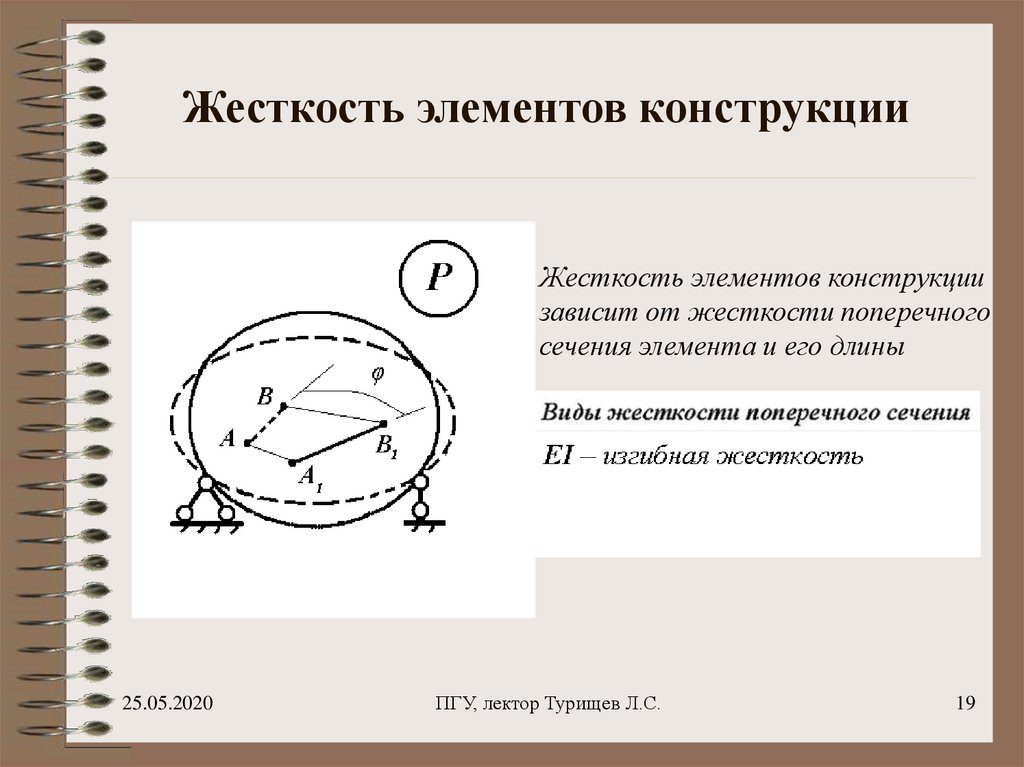
19. Жесткость элементов конструкции
Жесткость элементов конструкциизависит от жесткости поперечного
сечения элемента и его длины
25.05.2020
ПГУ, лектор Турищев Л.С.
19
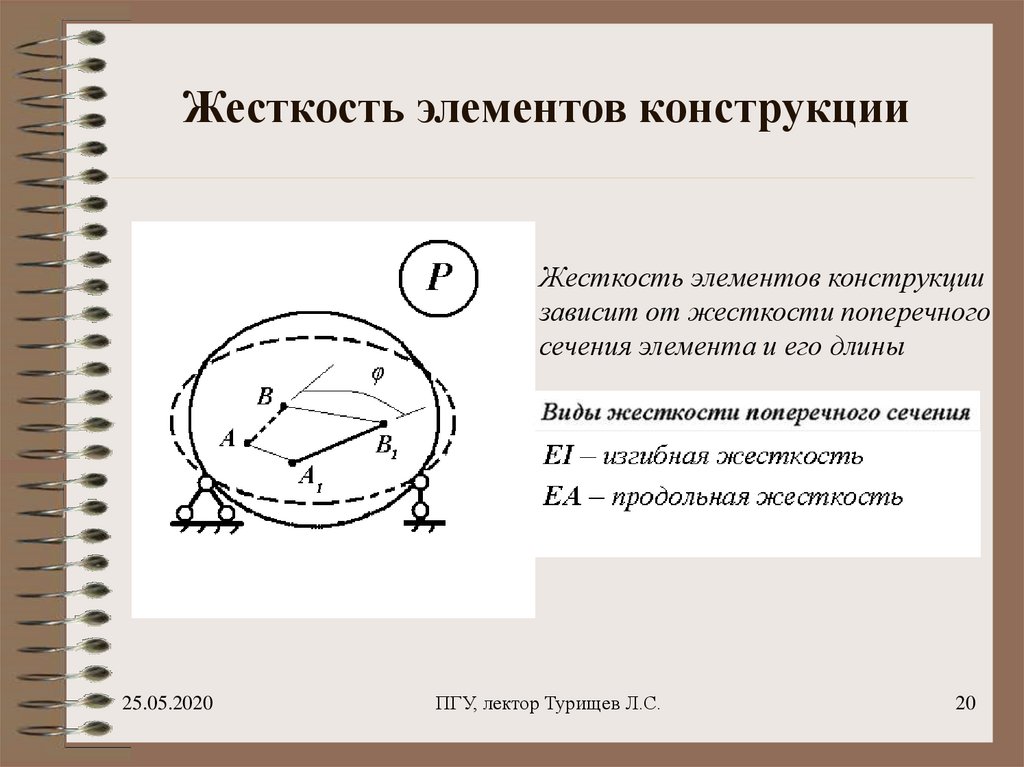
20. Жесткость элементов конструкции
Жесткость элементов конструкциизависит от жесткости поперечного
сечения элемента и его длины
25.05.2020
ПГУ, лектор Турищев Л.С.
20
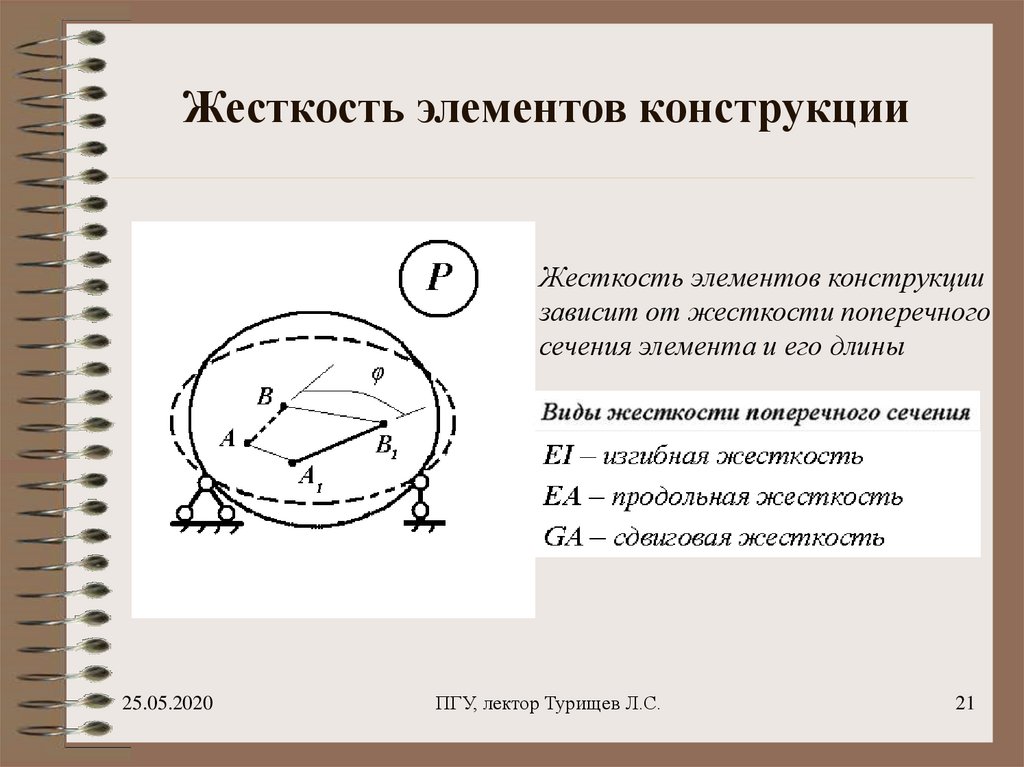
21. Жесткость элементов конструкции
Жесткость элементов конструкциизависит от жесткости поперечного
сечения элемента и его длины
25.05.2020
ПГУ, лектор Турищев Л.С.
21
22. Подходы к определению перемещений в конструкциях
Первый подходΔ1<< l
Согласно первому подходу определяются
перемещения, которые малы по сравнению с
размерами конструкции
Такой подход справедлив для жестких
конструкций, которые можно считать
линейно деформируемыми системами
25.05.2020
ПГУ, лектор Турищев Л.С.
22
23. Подходы к определению перемещений в конструкциях
Первый подходΔ1<< l
Согласно первому подходу определяются
перемещения, которые малы по сравнению с
размерами конструкции
Такой подход справедлив для жестких
конструкций, которые можно считать
линейно деформируемыми системами
Второй подход
Δ1,2 ~ l
25.05.2020
Второй подход связан с определением
больших перемещений. Перемещения
соизмеримы с размерами конструкции
Такой подход справедлив для гибких
конструкций, которые нельзя считать
линейно деформируемыми системами
ПГУ, лектор Турищев Л.С.
23
24. Перемещения конструкций, рассматриваемые в курсе
Малые перемещенияΔ1<< l
25.05.2020
ПГУ, лектор Турищев Л.С.
24
25. Формы определения перемещений конструкций, рассматриваемых в курсе
Аналитическая формаΔ1<< l
Матричная форма
25.05.2020
ПГУ, лектор Турищев Л.С.
25
26.
Какие есть вопросы?25.05.2020
ПГУ,
ПГУ,лектор
кафедра
Турищев
механики
Л.С.
26
27.
Тогда идем дальше.25.05.2020
ПГУ, лектор Турищев Л.С.
27
28. 2. Связь между внешними силами и перемещениями в линейно-деформируемых системах
25.05.2020ПГУ, лектор Турищев Л.С.
28
29. Полные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
29
30. Полные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
30
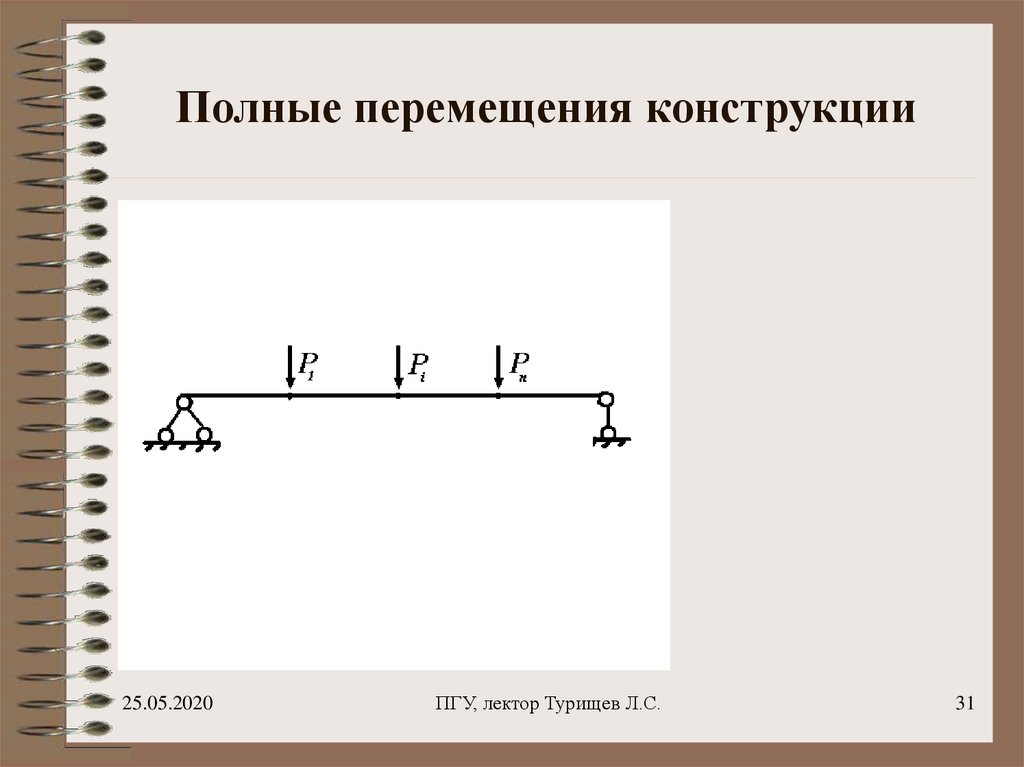
31. Полные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
31
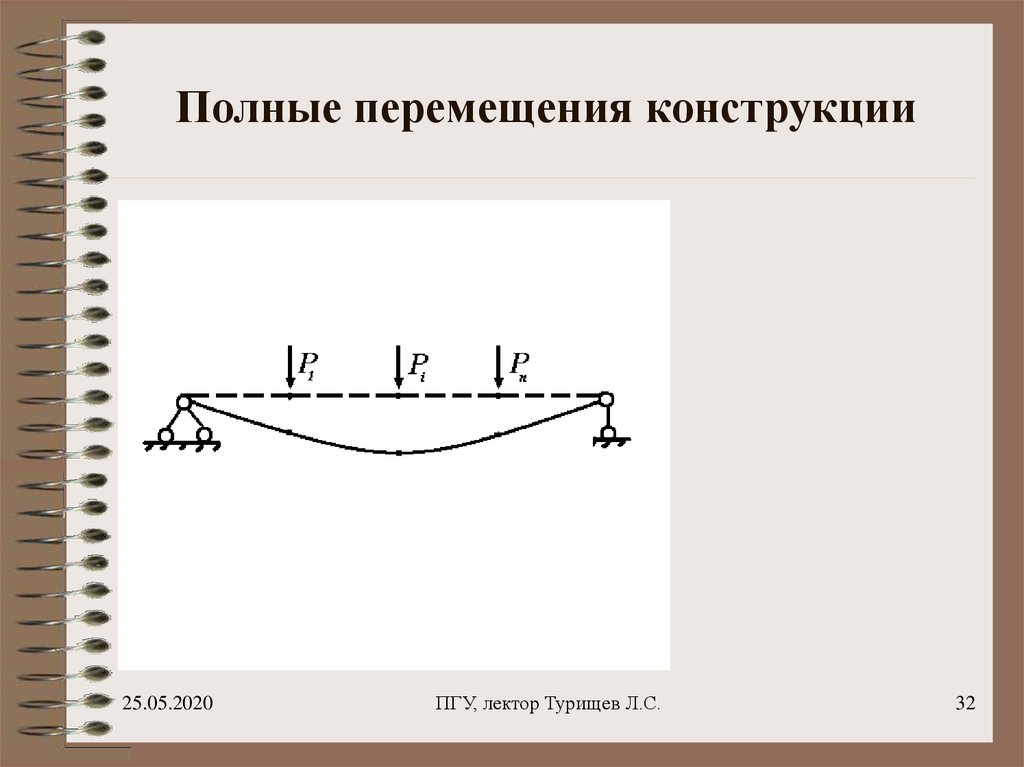
32. Полные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
32
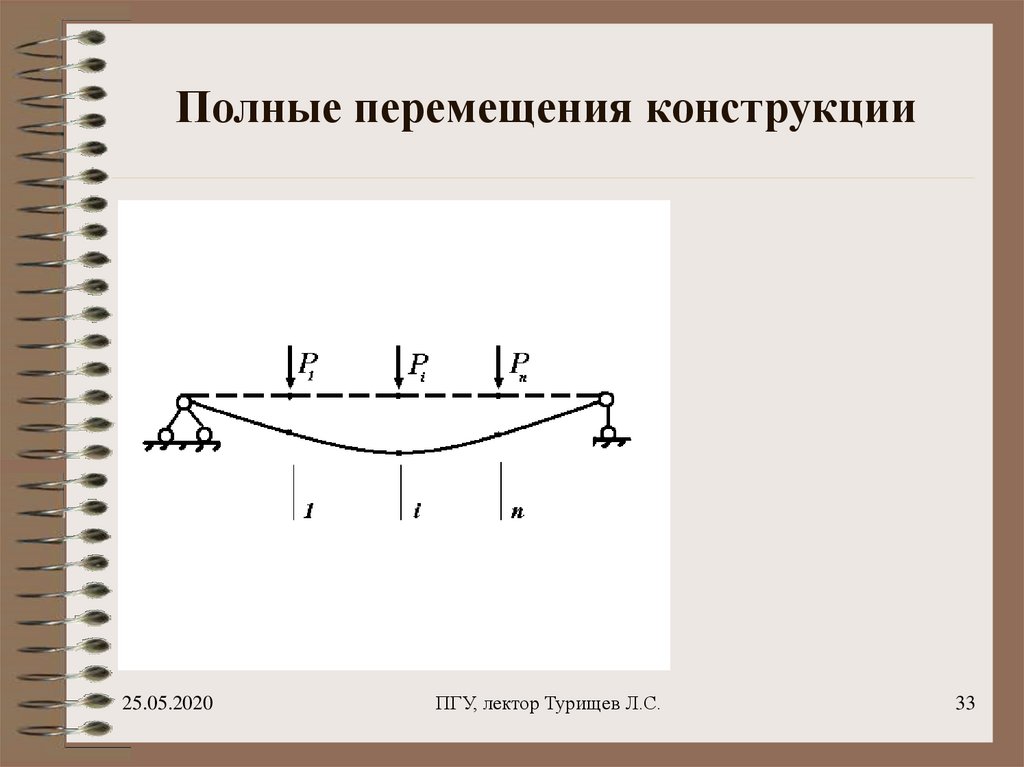
33. Полные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
33
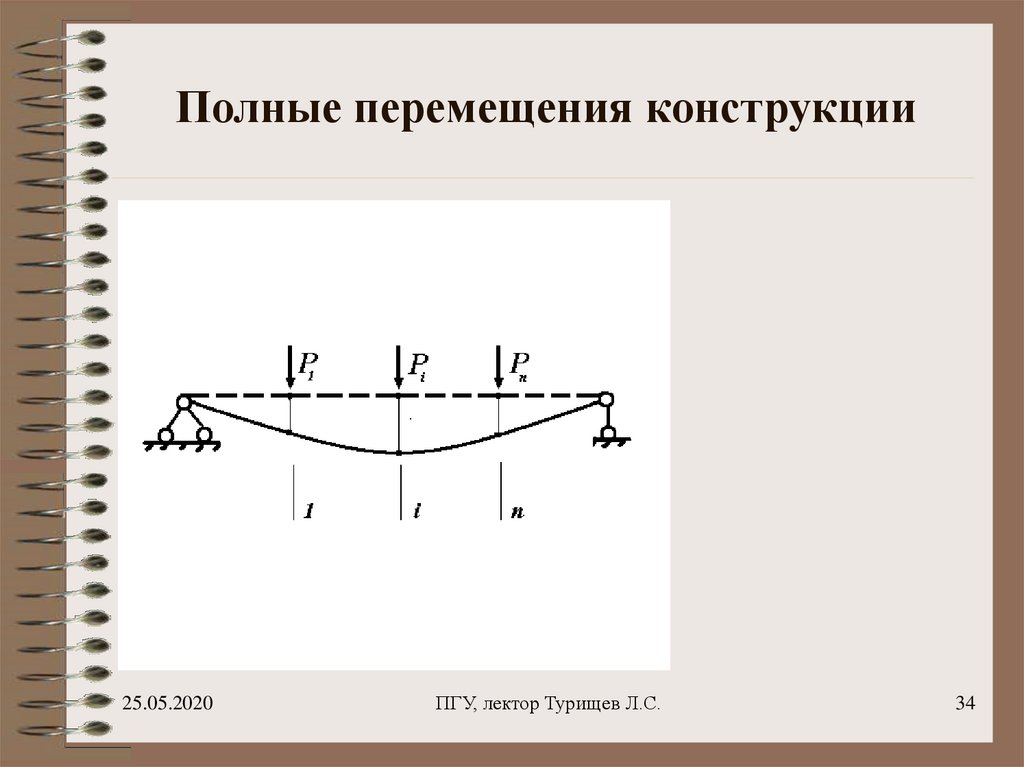
34. Полные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
34
35. Полные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
35
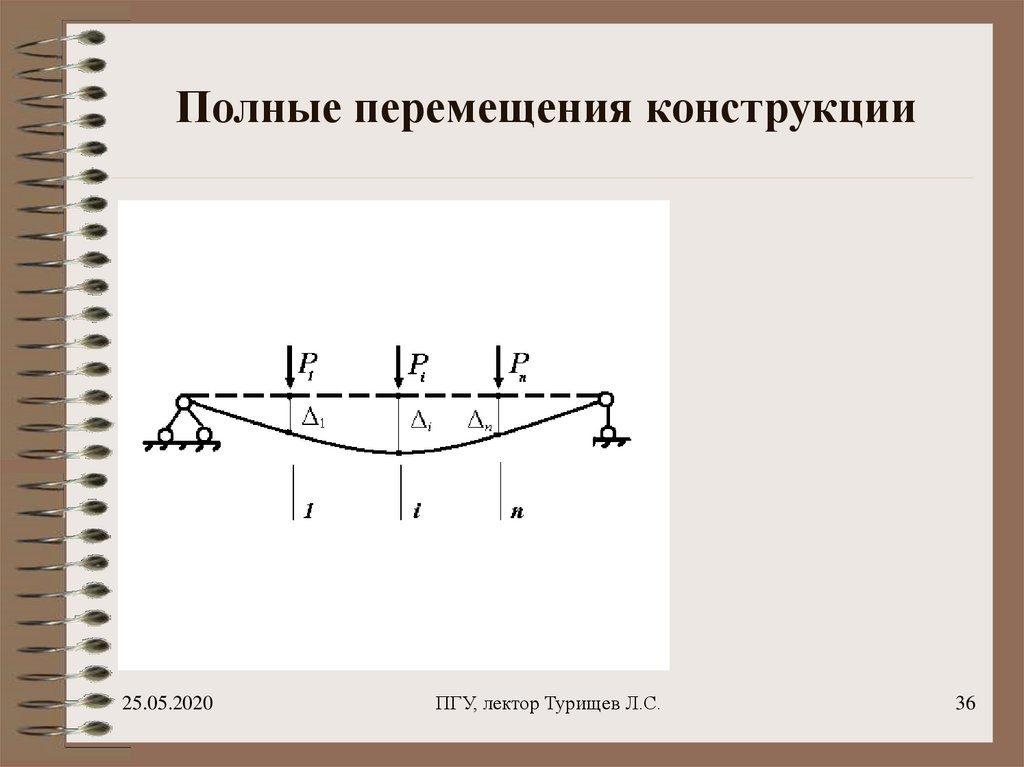
36. Полные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
36
37. Полные перемещения конструкции
ii 1,...,n
Перемещения, происходящие в
конструкции от действия всех сил
одновременно
Индекс указывает номер
направления, по которым
возникают перемещения
25.05.2020
ПГУ, лектор Турищев Л.С.
37
38. Частичные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
38
39. Частичные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
39
40. Частичные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
40
41. Частичные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
41
42. Частичные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
42
43. Частичные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
43
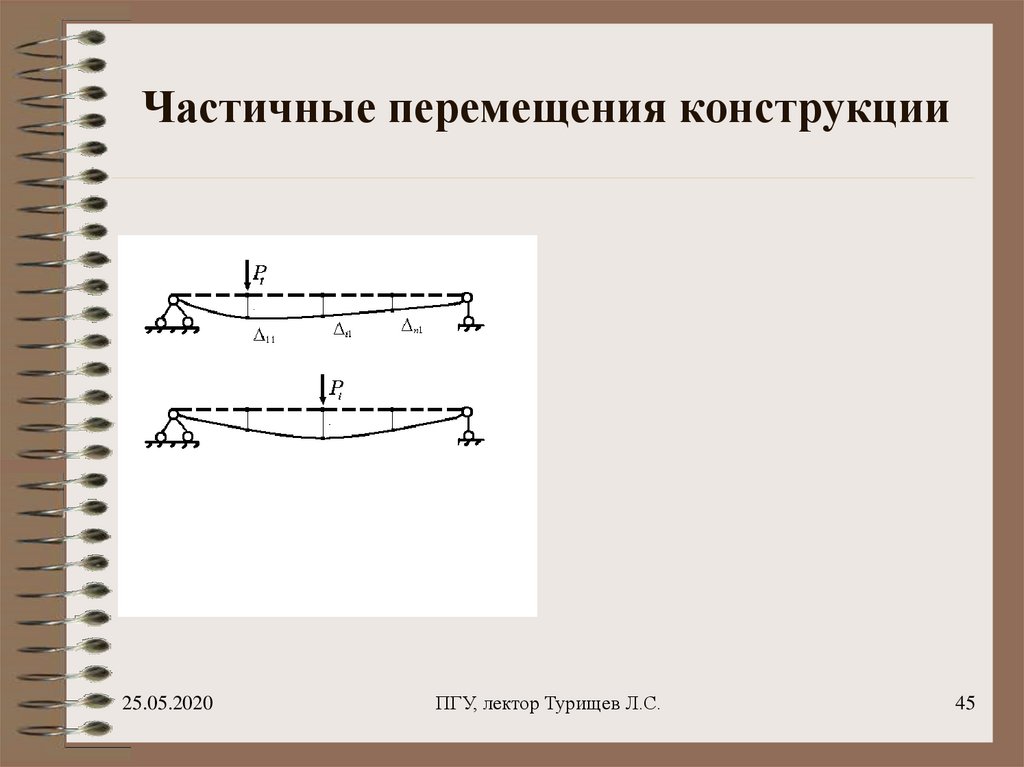
44. Частичные перемещения конструкции
Первый индекс указывает номернаправления, по которому
перемещение происходит
Второй индекс указывает номер
направления, по которому действует
сила, вызывающая это перемещение
25.05.2020
ПГУ, лектор Турищев Л.С.
44
45. Частичные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
45
46. Частичные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
46
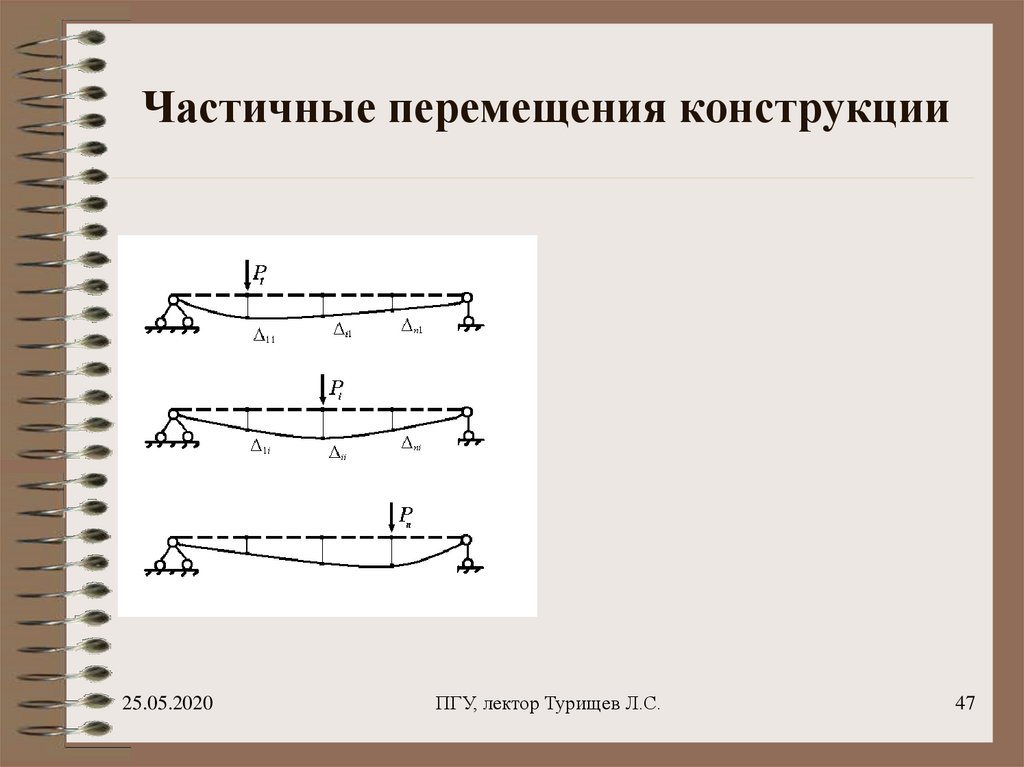
47. Частичные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
47
48. Частичные перемещения конструкции
iji, j 1,..., n
Перемещения, которые возникают
в конструкции при раздельном
приложении сил
25.05.2020
ПГУ, лектор Турищев Л.С.
48
49. Единичные перемещения конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
49
50. Единичные перемещения конструкции
~Pj 1 ( j 1,...,n)
Перемещения, которые возникают
в конструкции от действия
безразмерных сил равных единице
по направлению сил, приложенных
к конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
50
51. Единичные перемещения конструкции
~Pj 1 ( j 1,...,n)
Перемещения, которые возникают
в конструкции от действия
безразмерных сил равных единице
по направлению сил, приложенных
к конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
51
52. Единичные перемещения конструкции
~Pj 1 ( j 1,...,n)
Перемещения, которые возникают
в конструкции от действия
безразмерных сил равных единице
по направлению сил, приложенных
к конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
52
53. Единичные перемещения конструкции
~Pj 1 ( j 1,...,n)
Перемещения, которые возникают
в конструкции от действия
безразмерных сил равных единице
по направлению сил, приложенных
к конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
53
54. Единичные перемещения конструкции
~Pj 1 ( j 1,...,n)
Перемещения, которые возникают
в конструкции от действия
безразмерных сил равных единице
по направлению сил, приложенных
к конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
54
55. Единичные перемещения конструкции
~Pj 1 ( j 1,...,n)
Перемещения, которые возникают
в конструкции от действия
безразмерных сил равных единице
по направлению сил, приложенных
к конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
55
56. Единичные перемещения конструкции
~Pj 1 ( j 1,...,n)
Перемещения, которые возникают
в конструкции от действия
безразмерных сил равных единице
по направлению сил, приложенных
к конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
56
57. Единичные перемещения конструкции
~Pj 1 ( j 1,...,n)
Перемещения, которые возникают
в конструкции от действия
безразмерных сил равных единице
по направлению сил, приложенных
к конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
57
58. Единичные перемещения конструкции
~Pj 1 ( j 1,...,n)
Перемещения, которые возникают
в конструкции от действия
безразмерных сил равных единице
по направлению сил, приложенных
к конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
58
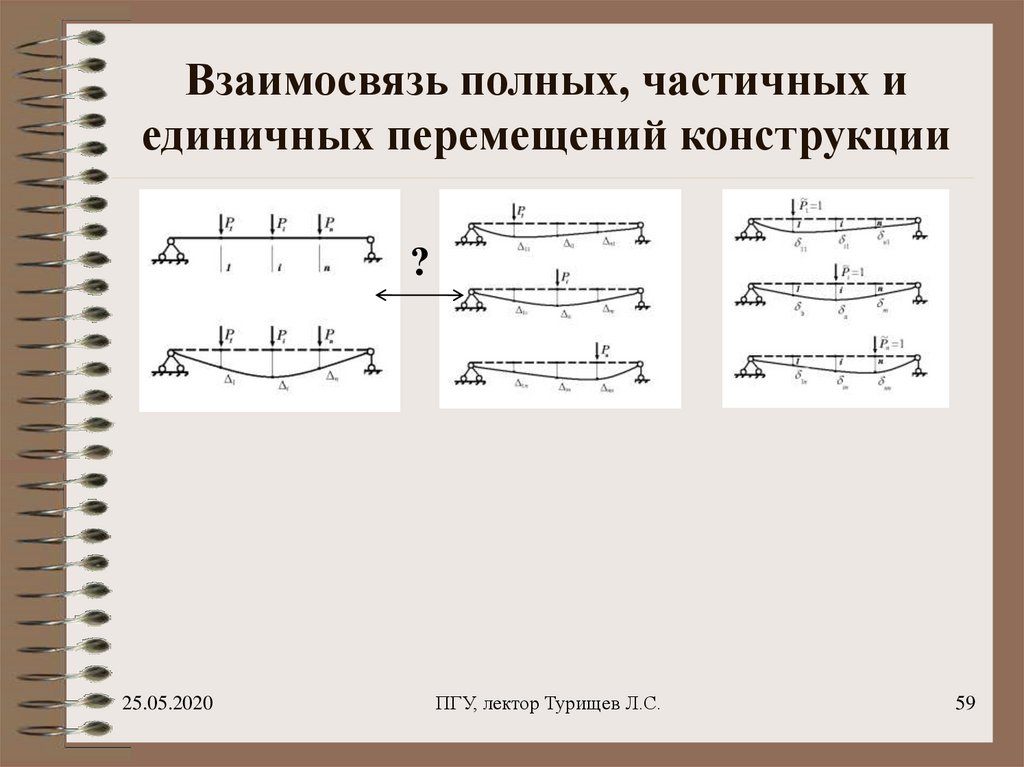
59. Взаимосвязь полных, частичных и единичных перемещений конструкции
?25.05.2020
ПГУ, лектор Турищев Л.С.
59
60. Взаимосвязь полных, частичных и единичных перемещений конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
60
61. Взаимосвязь полных, частичных и единичных перемещений конструкции
?Вытекает из принципа
независимости действия
сил
25.05.2020
ПГУ, лектор Турищев Л.С.
61
62. Взаимосвязь полных, частичных и единичных перемещений конструкции
Вытекает из принципанезависимости действия
сил
25.05.2020
ПГУ, лектор Турищев Л.С.
62
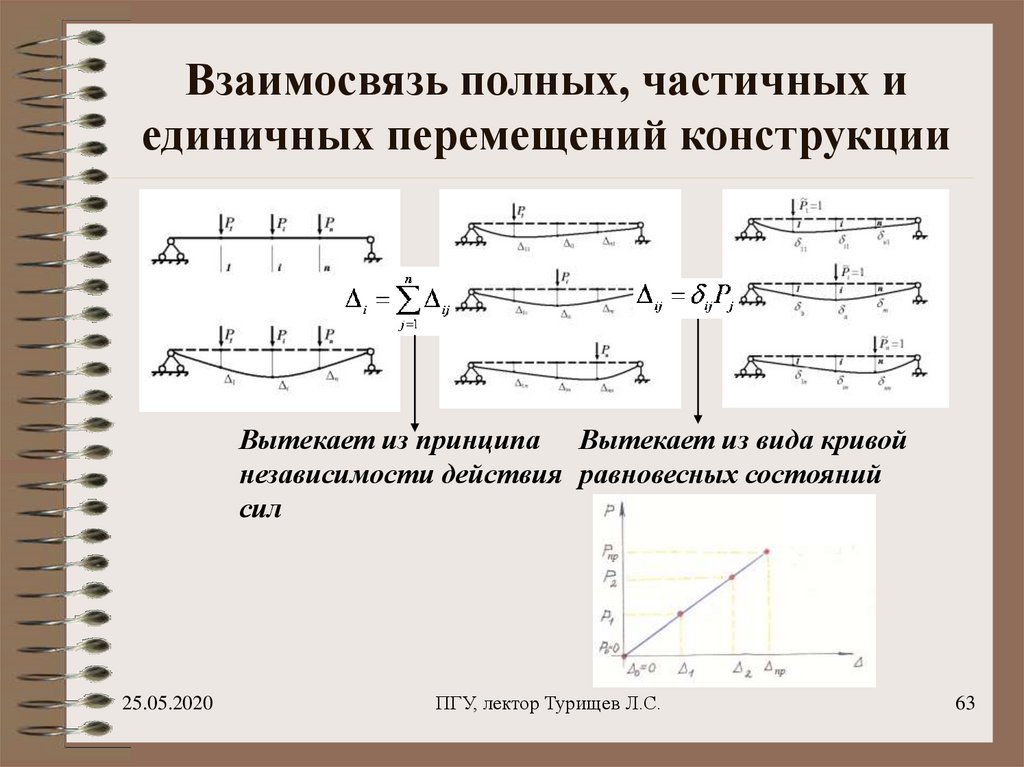
63. Взаимосвязь полных, частичных и единичных перемещений конструкции
Вытекает из принципа Вытекает из вида кривойнезависимости действия равновесных состояний
сил
25.05.2020
ПГУ, лектор Турищев Л.С.
63
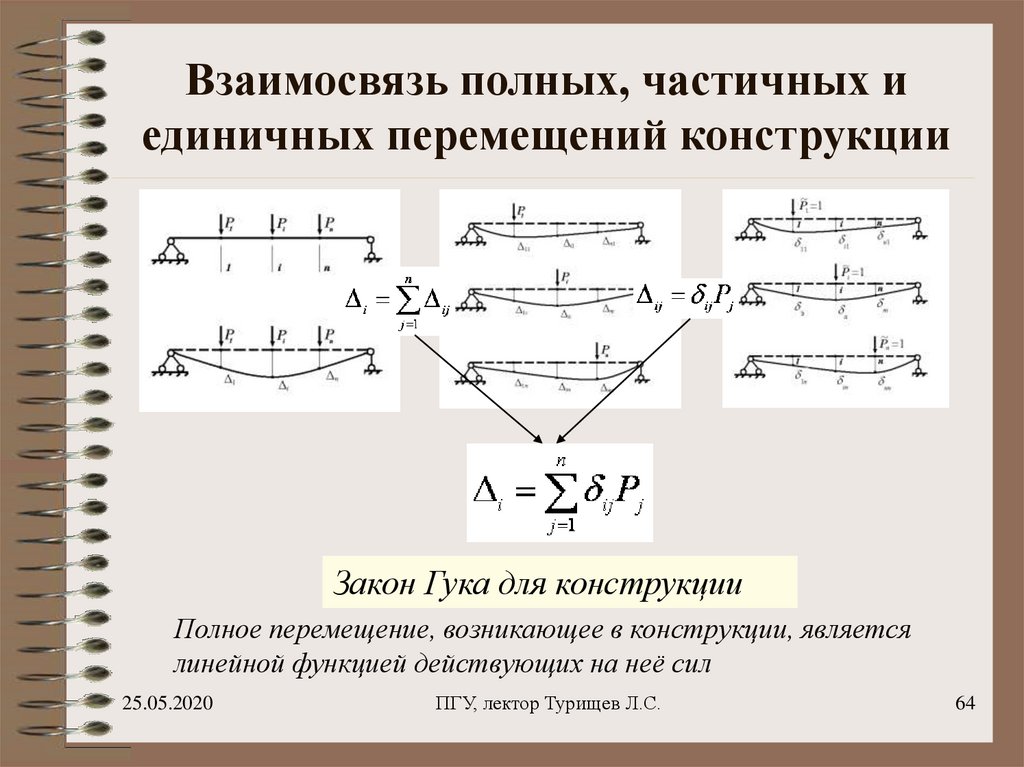
64. Взаимосвязь полных, частичных и единичных перемещений конструкции
Закон Гука для конструкцииПолное перемещение, возникающее в конструкции, является
линейной функцией действующих на неё сил
25.05.2020
ПГУ, лектор Турищев Л.С.
64
65.
Какие есть вопросы?25.05.2020
ПГУ, лектор Турищев Л.С.
65
66.
Тогда идем дальше.25.05.2020
ПГУ, лектор Турищев Л.С.
66
67. 3. Аналитическая форма определения перемещений в плоской стержневой конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
67
68. Постановка вопроса
Система статически определимаяили статически неопределимая
25.05.2020
ПГУ, лектор Турищев Л.С.
68
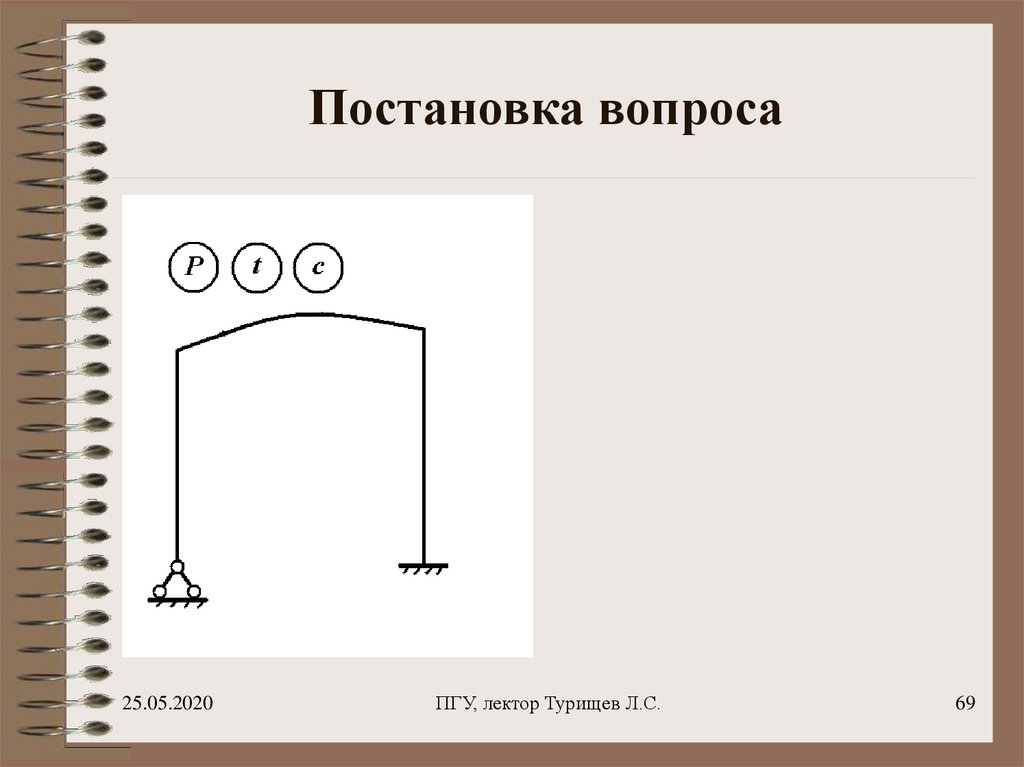
69. Постановка вопроса
25.05.2020ПГУ, лектор Турищев Л.С.
69
70. Постановка вопроса
12
25.05.2020
j
ПГУ, лектор Турищев Л.С.
70
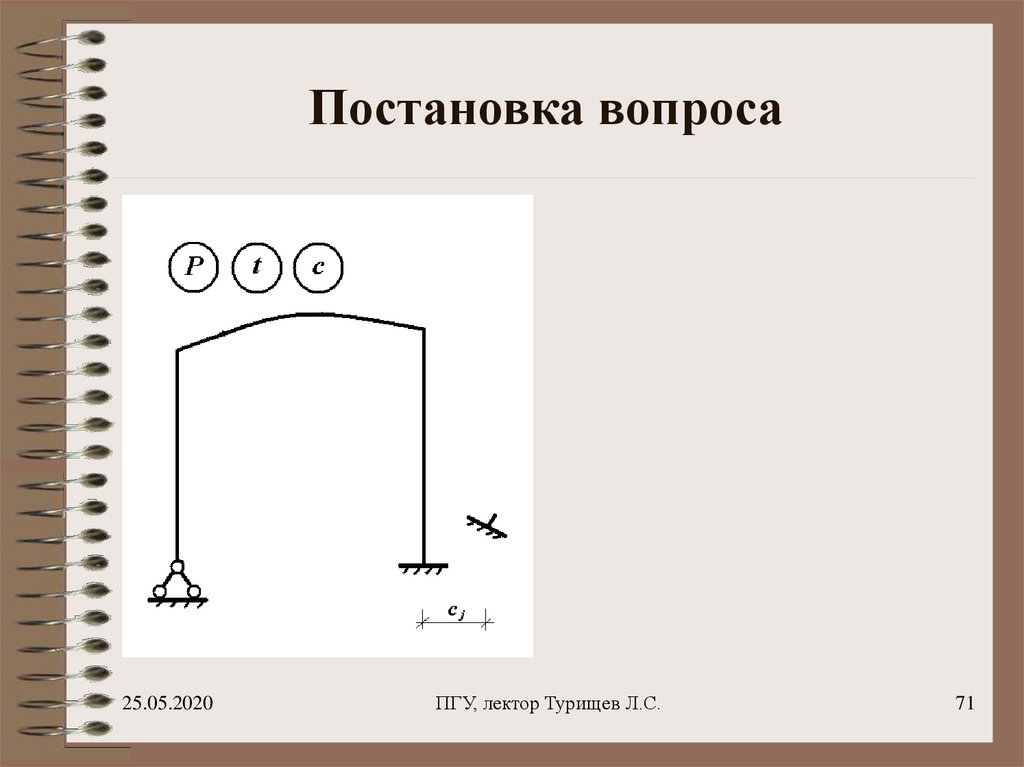
71. Постановка вопроса
25.05.2020ПГУ, лектор Турищев Л.С.
71
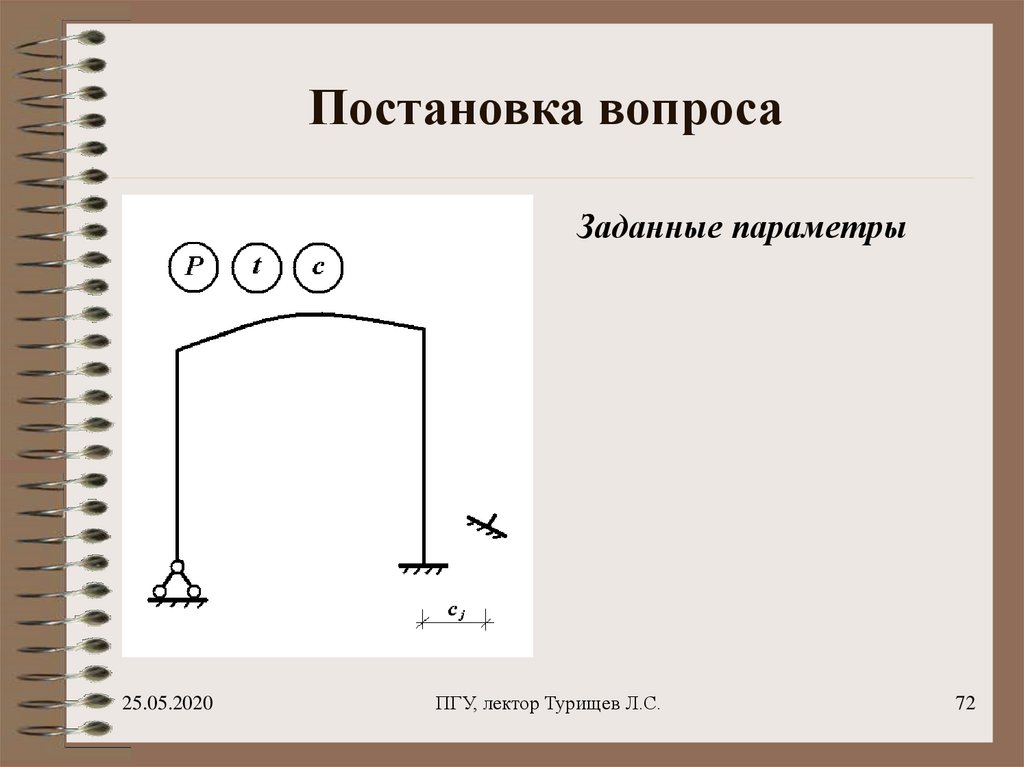
72. Постановка вопроса
Заданные параметры25.05.2020
ПГУ, лектор Турищев Л.С.
72
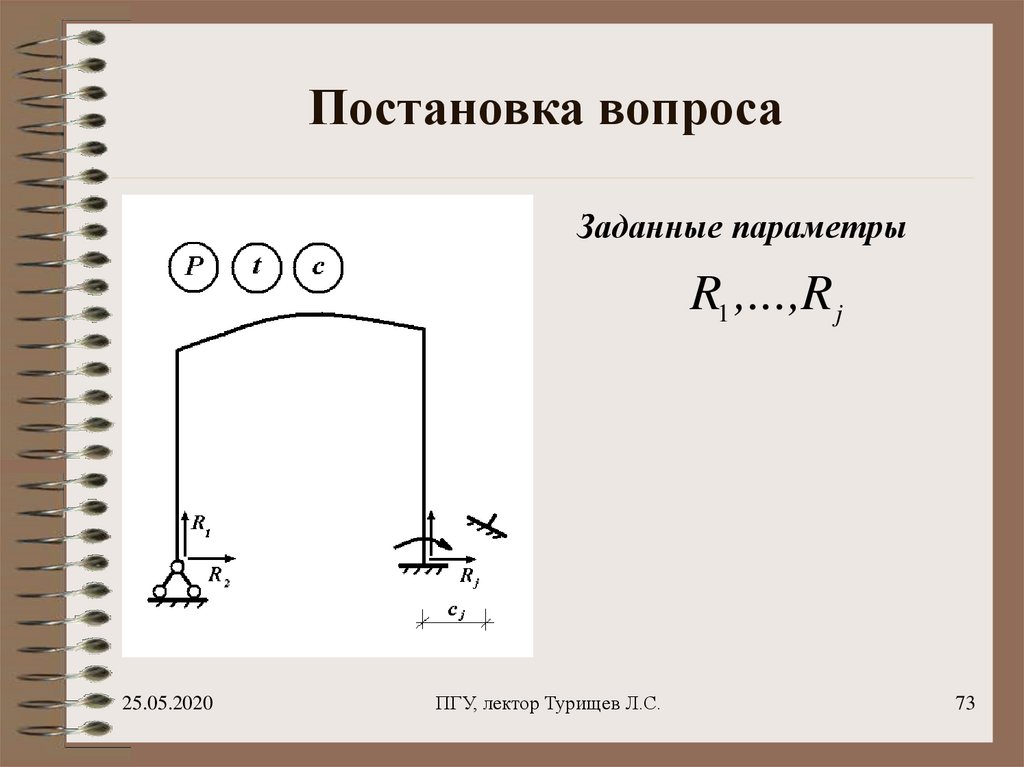
73. Постановка вопроса
Заданные параметрыR1 ,...,R j
25.05.2020
ПГУ, лектор Турищев Л.С.
73
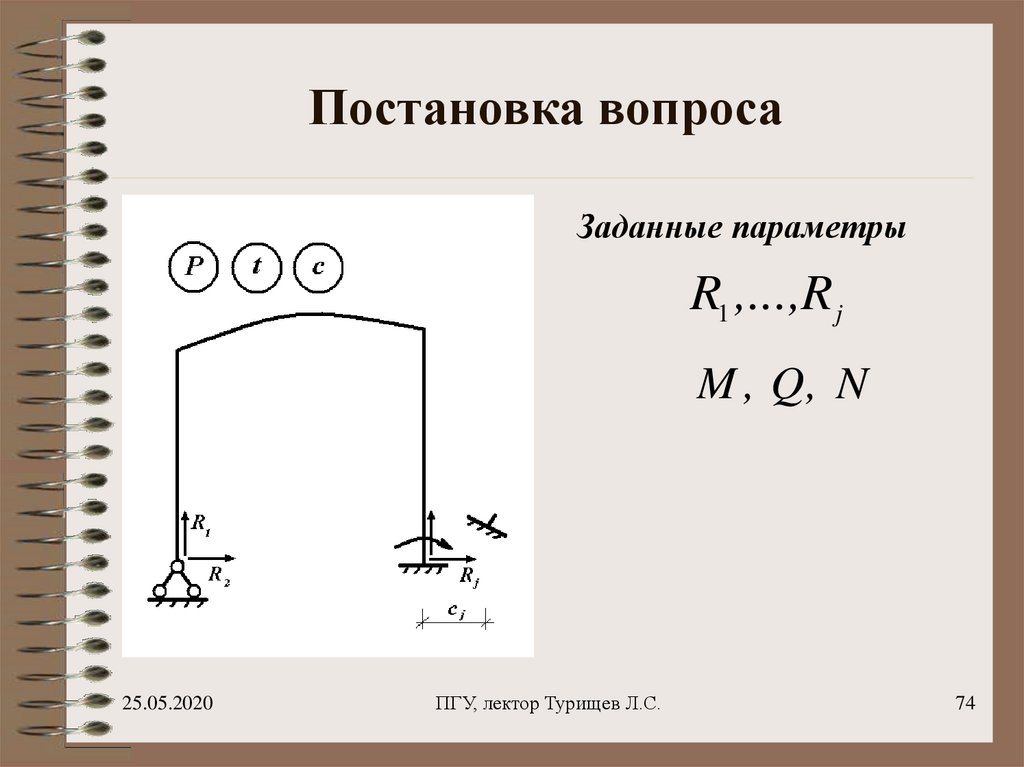
74. Постановка вопроса
Заданные параметрыR1 ,...,R j
M , Q, N
25.05.2020
ПГУ, лектор Турищев Л.С.
74
75. Постановка вопроса
Заданные параметрыR1 ,...,R j
M , Q, N
,
25.05.2020
ПГУ, лектор Турищев Л.С.
75
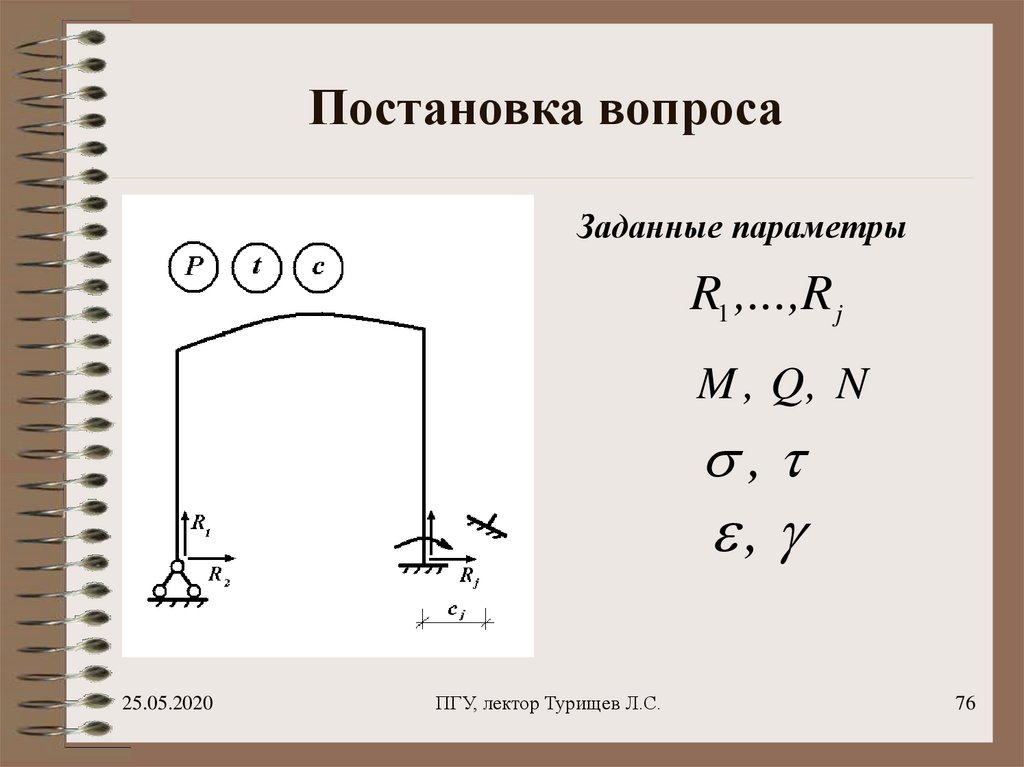
76. Постановка вопроса
Заданные параметрыR1 ,...,R j
M , Q, N
,
,
25.05.2020
ПГУ, лектор Турищев Л.С.
76
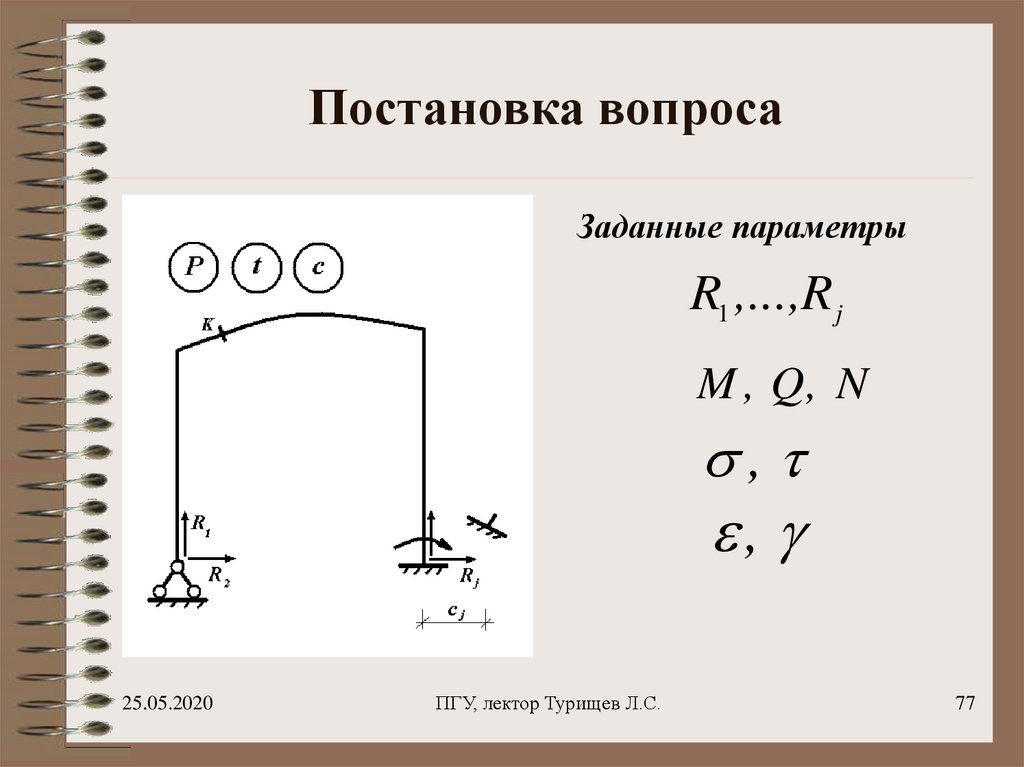
77. Постановка вопроса
Заданные параметрыR1 ,...,R j
M , Q, N
,
,
25.05.2020
ПГУ, лектор Турищев Л.С.
77
78. Постановка вопроса
Заданные параметрыR1 ,...,R j
M , Q, N
,
,
25.05.2020
ПГУ, лектор Турищев Л.С.
78
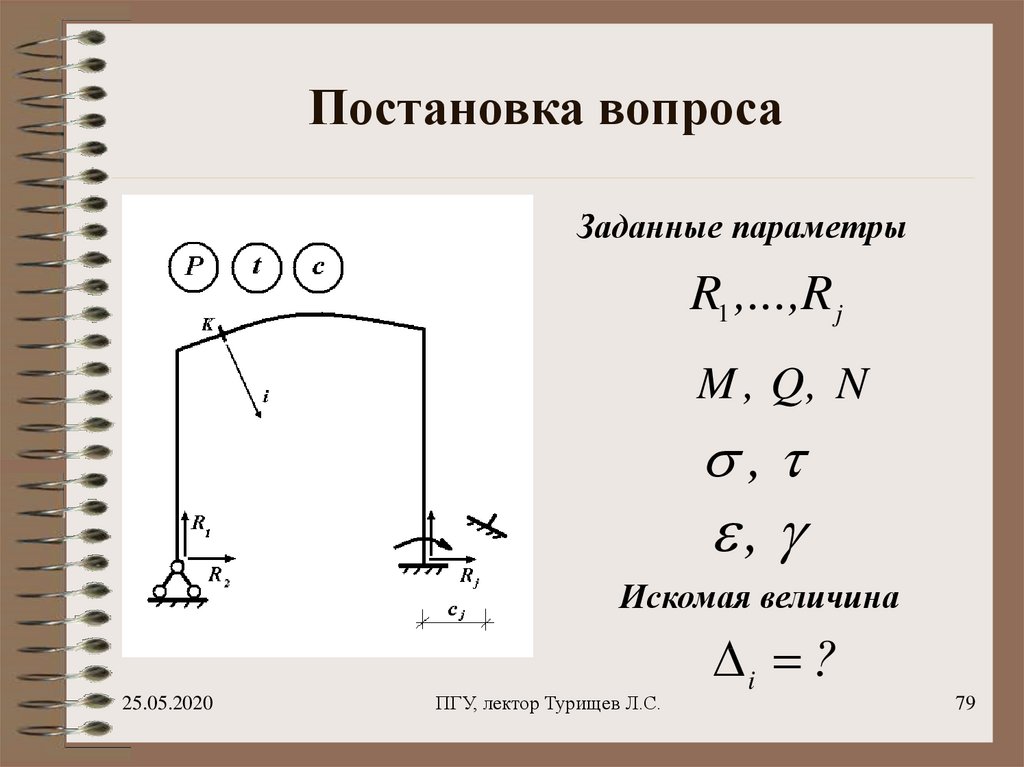
79. Постановка вопроса
Заданные параметрыR1 ,...,R j
M , Q, N
,
,
Искомая величина
25.05.2020
ПГУ, лектор Турищев Л.С.
i ?
79
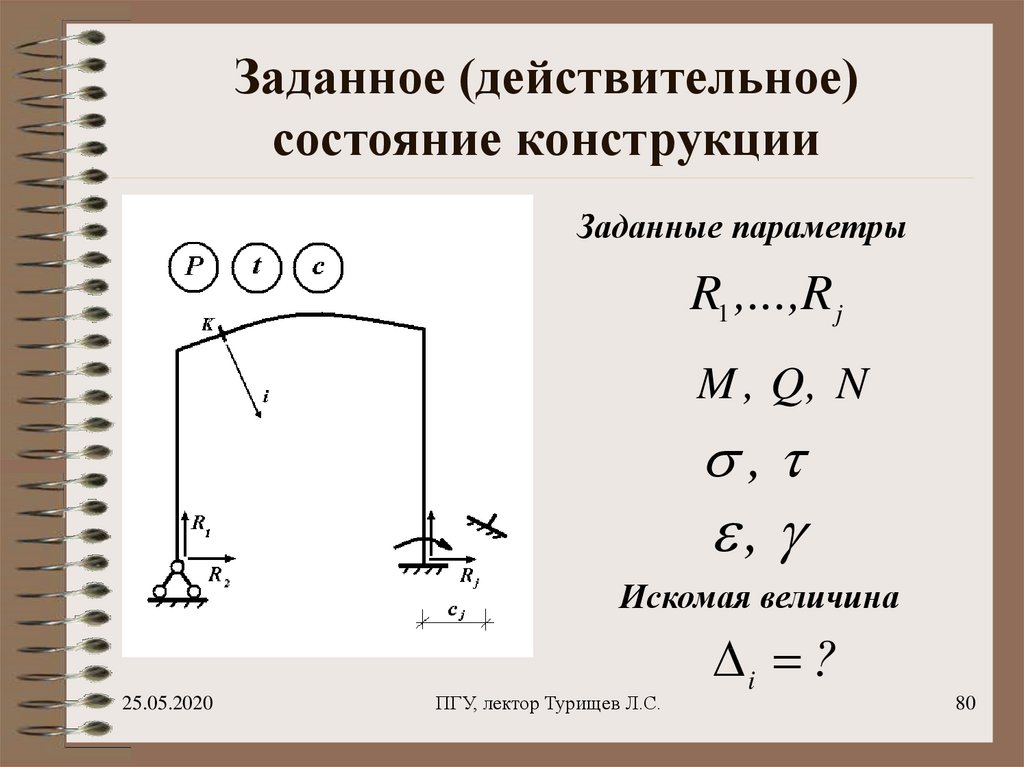
80. Заданное (действительное) состояние конструкции
Заданные параметрыR1 ,...,R j
M , Q, N
,
,
Искомая величина
25.05.2020
ПГУ, лектор Турищев Л.С.
i ?
80
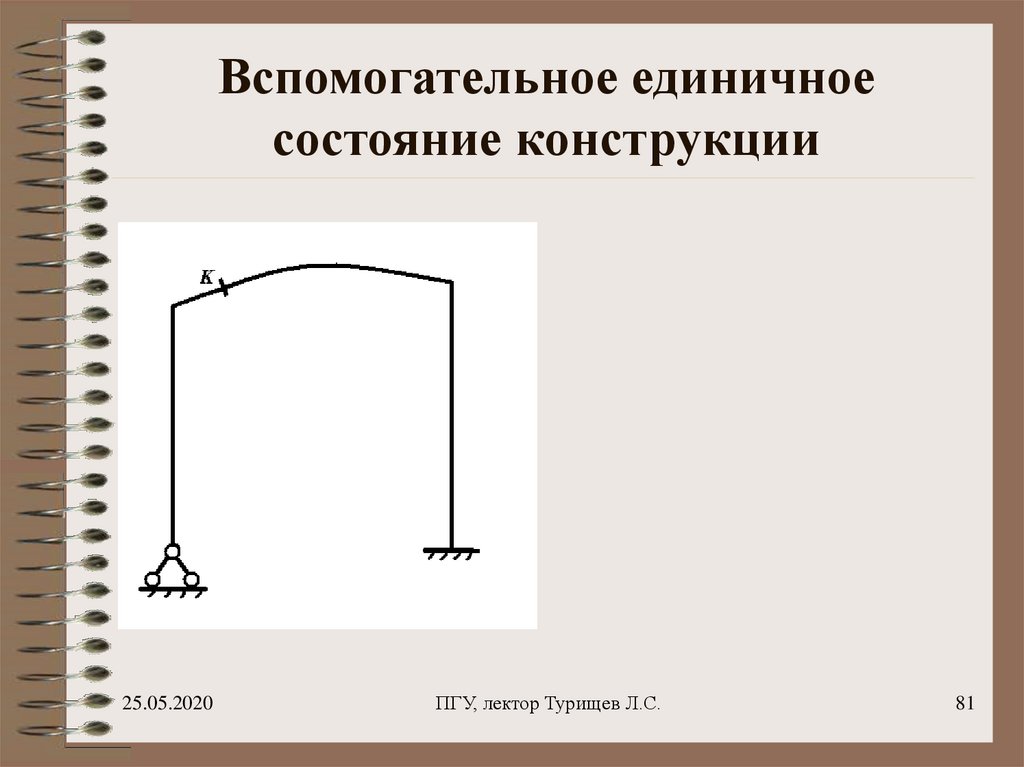
81. Вспомогательное единичное состояние конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
81
82. Вспомогательное единичное состояние конструкции
25.05.2020ПГУ, лектор Турищев Л.С.
82
83. Вспомогательное единичное состояние конструкции
Заданные параметры25.05.2020
ПГУ, лектор Турищев Л.С.
83
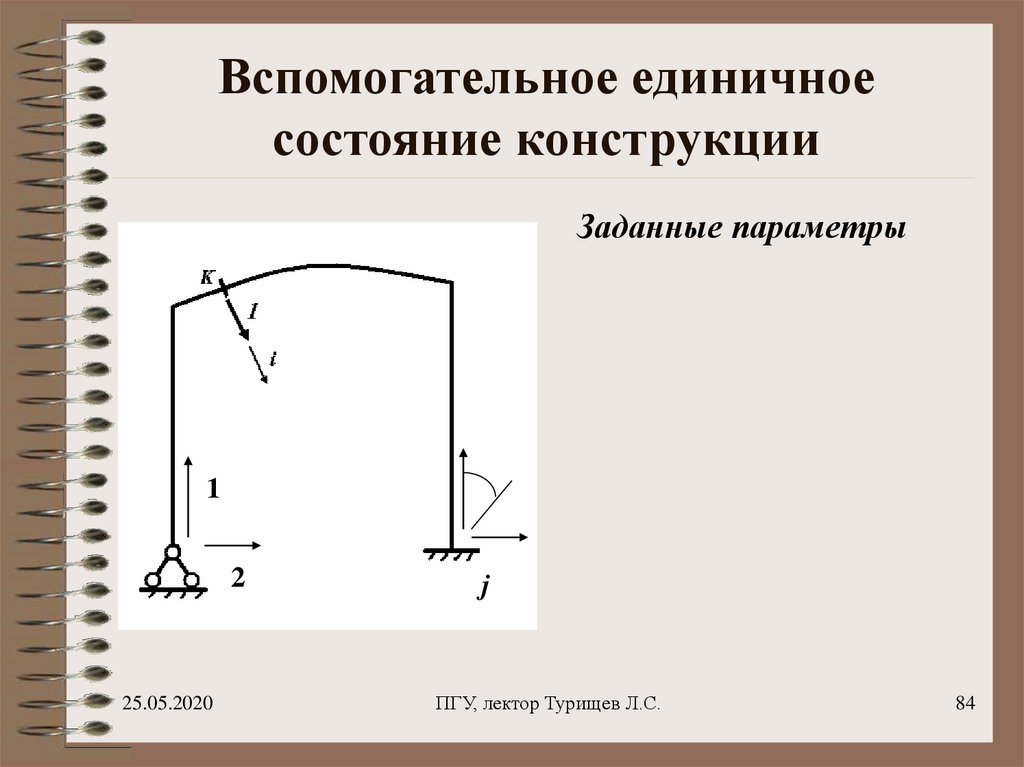
84. Вспомогательное единичное состояние конструкции
Заданные параметры1
2
25.05.2020
j
ПГУ, лектор Турищев Л.С.
84
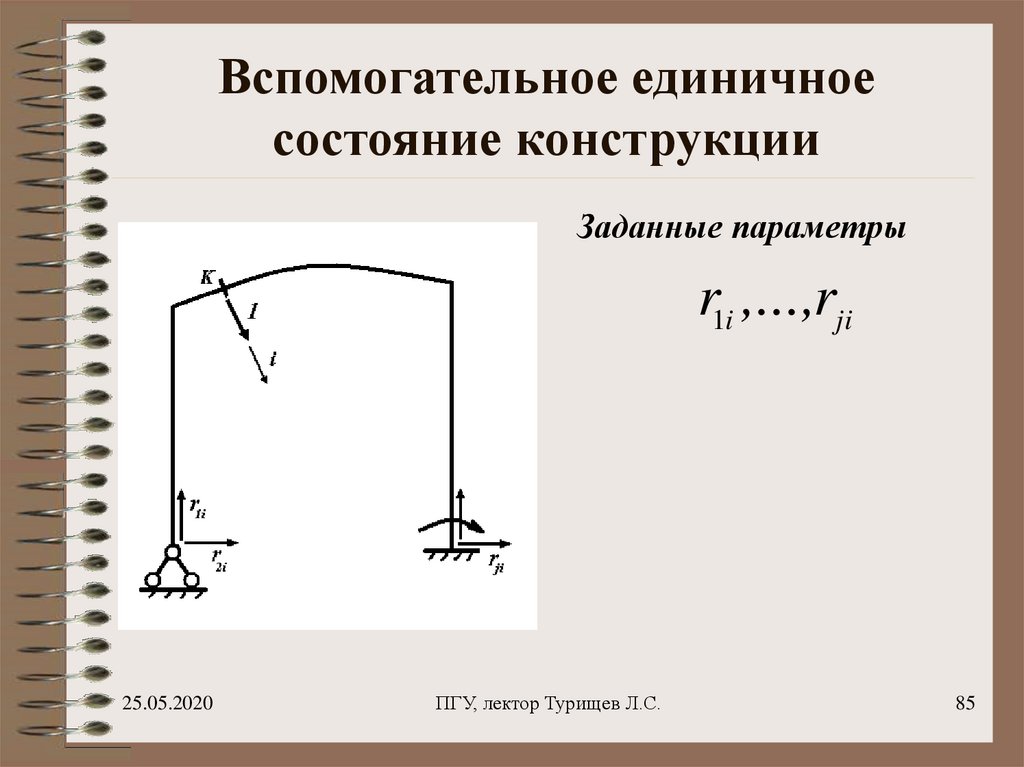
85. Вспомогательное единичное состояние конструкции
Заданные параметрыr1i ,...,rji
25.05.2020
ПГУ, лектор Турищев Л.С.
85
86. Вспомогательное единичное состояние конструкции
Заданные параметрыr1i ,...,rji
mi , qi , ni
25.05.2020
ПГУ, лектор Турищев Л.С.
86
87. Вспомогательное единичное состояние конструкции
Заданные параметрыr1i ,...,rji
mi , qi , ni
i , i
25.05.2020
ПГУ, лектор Турищев Л.С.
87
88. Вспомогательное единичное состояние конструкции
Заданные параметрыr1i ,...,rji
mi , qi , ni
i , i
i , i
25.05.2020
ПГУ, лектор Турищев Л.С.
88
89. Универсальная формула для определения перемещений
В основе вывода лежит принцип возможныхперемещений для деформируемой системы
25.05.2020
ПГУ, лектор Турищев Л.С.
89
90. Универсальная формула для определения перемещений
i rjic j i i dAdsj
25.05.2020
k
l A
ПГУ, лектор Турищев Л.С.
90
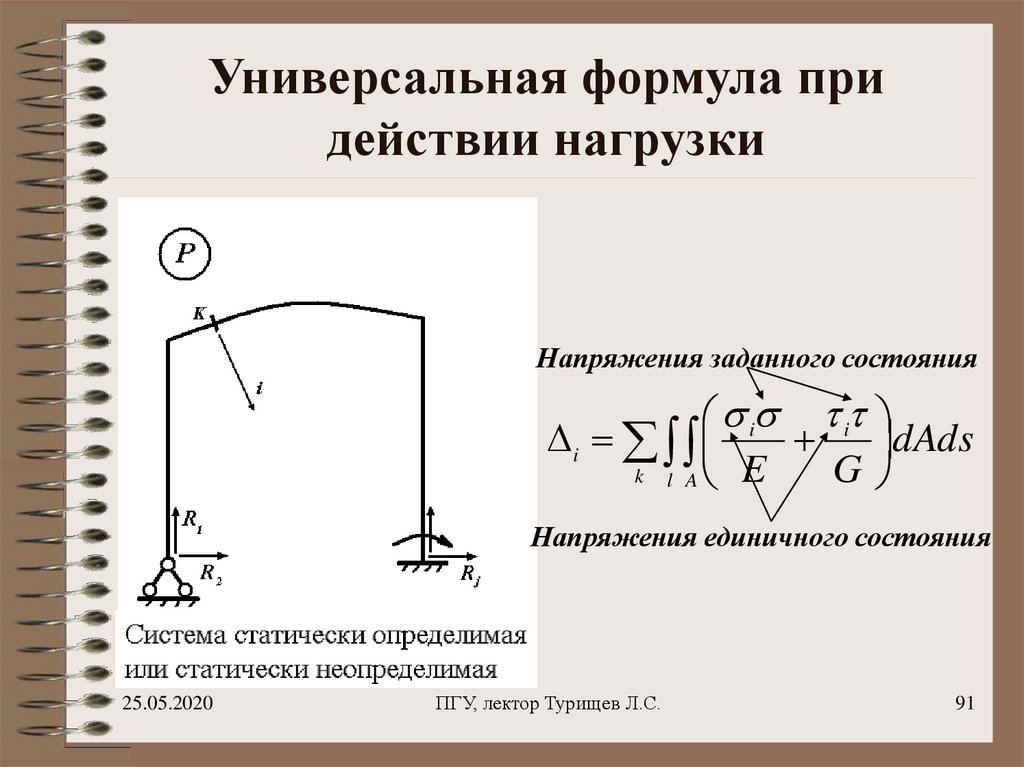
91. Универсальная формула при действии нагрузки
Напряжения заданного состоянияi i
i
dAds
G
k l A E
Напряжения единичного состояния
25.05.2020
ПГУ, лектор Турищев Л.С.
91
92.
Какие есть вопросы?25.05.2020
ПГУ, лектор Турищев Л.С.
92
93.
Тогда идем дальше.25.05.2020
ПГУ, лектор Турищев Л.С.
93
94. 4. Рабочая формула для определения перемещений от действия нагрузки
25.05.2020ПГУ, лектор Турищев Л.С.
94
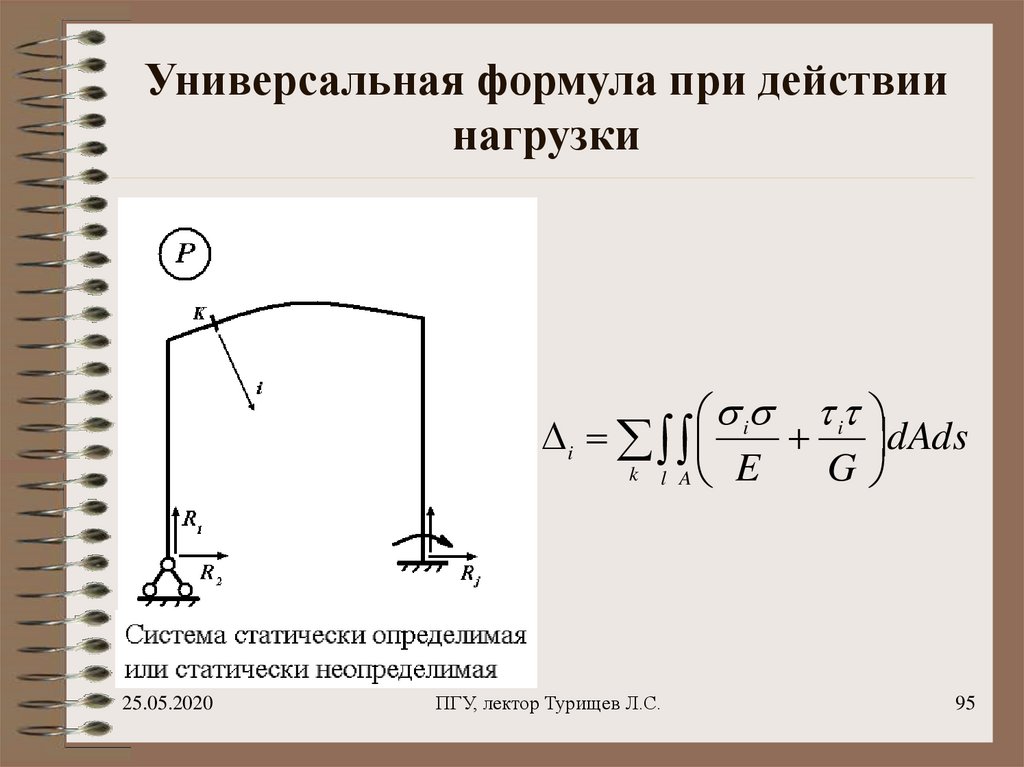
95. Универсальная формула при действии нагрузки
i ii
dAds
G
k l A E
25.05.2020
ПГУ, лектор Турищев Л.С.
95
96. Рабочая формула для определения перемещений от нагрузки
ii
i
dA dA ds
G
k l A E
A
i
25.05.2020
ПГУ, лектор Турищев Л.С.
96
97. Рабочая формула для определения перемещений от нагрузки
ii
i
dA dA ds
G
k l A E
A
mi M
i
ds
k l EI z
Доля перемещения,
вызванная изгибными
деформациями элементов
конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
97
98. Рабочая формула для определения перемещений от нагрузки
ii
i
dA dA ds
G
k l A E
A
mi M
ni N
i
ds
ds
k l EI z
k l EA
Доля перемещения,
вызванная изгибными
деформациями элементов
конструкции
Доля перемещения,
вызванная продольными
деформациями элементов
конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
98
99. Рабочая формула для определения перемещений от нагрузки
ii
i
dA dA ds
G
k l A E
A
Формула Максвелла-Мора
mi M
ni N
qiQ
i
ds
ds k
ds
k l EI z
k l EA
k
l GA
Доля перемещения,
вызванная изгибными
деформациями элементов
конструкции
Доля перемещения,
вызванная продольными
деформациями элементов
конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
Доля перемещения,
вызванная сдвиговыми
деформациями элементов
конструкции
99
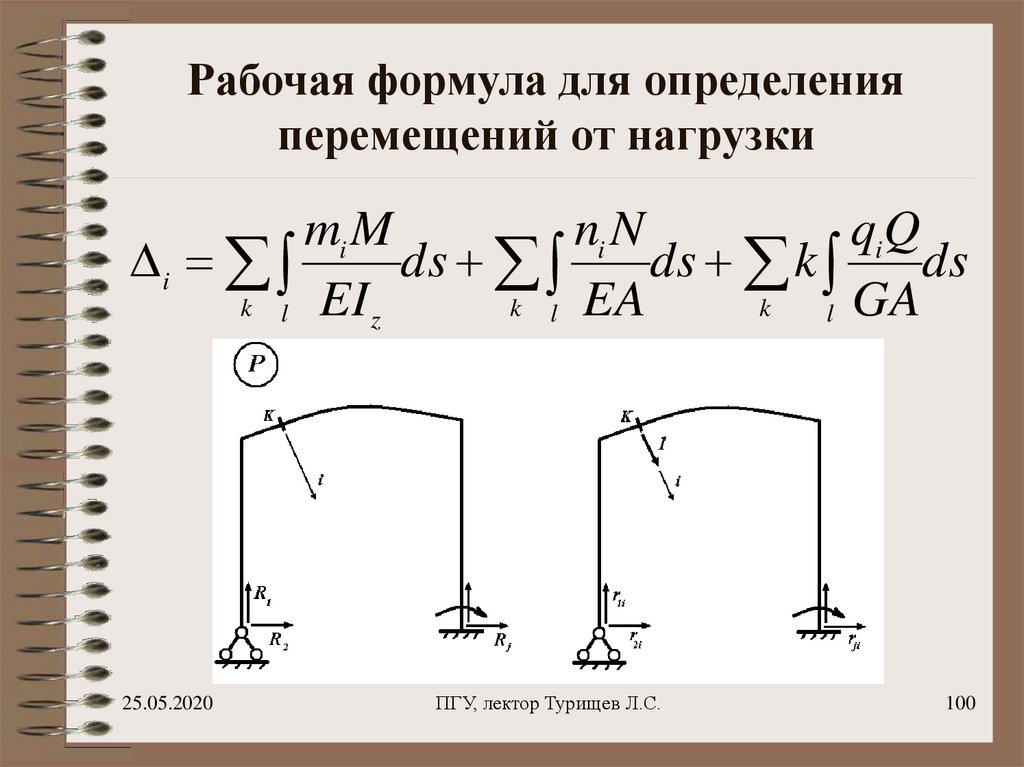
100. Рабочая формула для определения перемещений от нагрузки
mi Mni N
qiQ
i
ds
ds k
ds
k l EI z
k l EA
k
l GA
25.05.2020
ПГУ, лектор Турищев Л.С.
100
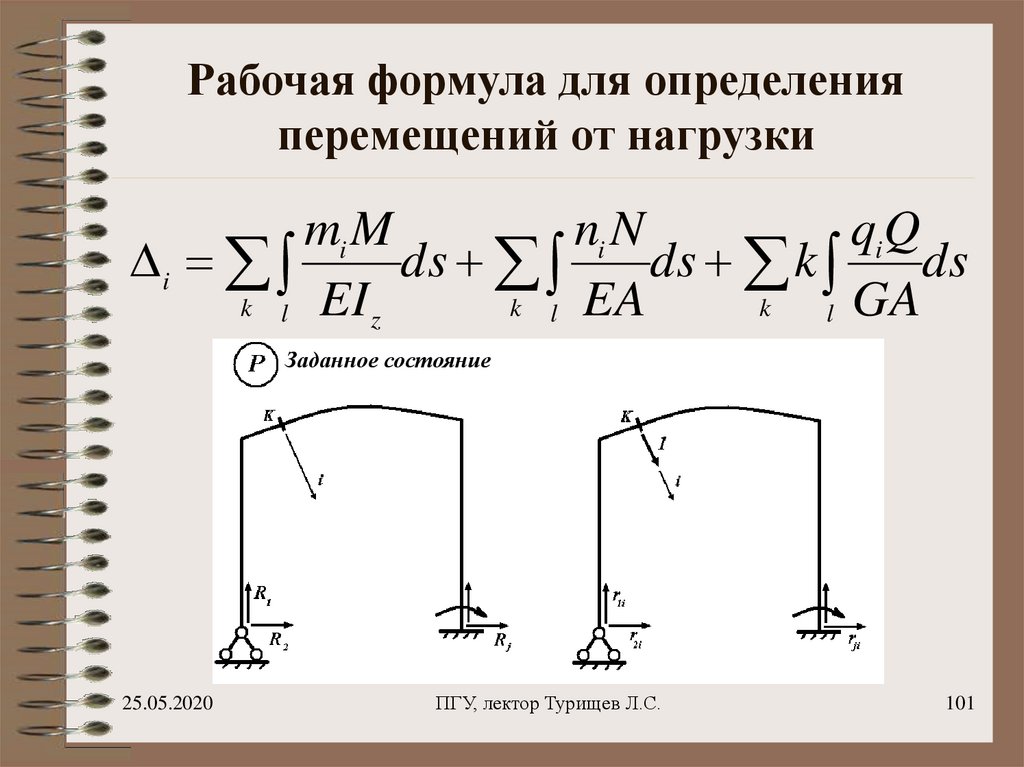
101. Рабочая формула для определения перемещений от нагрузки
mi Mni N
qiQ
i
ds
ds k
ds
k l EI z
k l EA
k
l GA
Заданное состояние
25.05.2020
ПГУ, лектор Турищев Л.С.
101
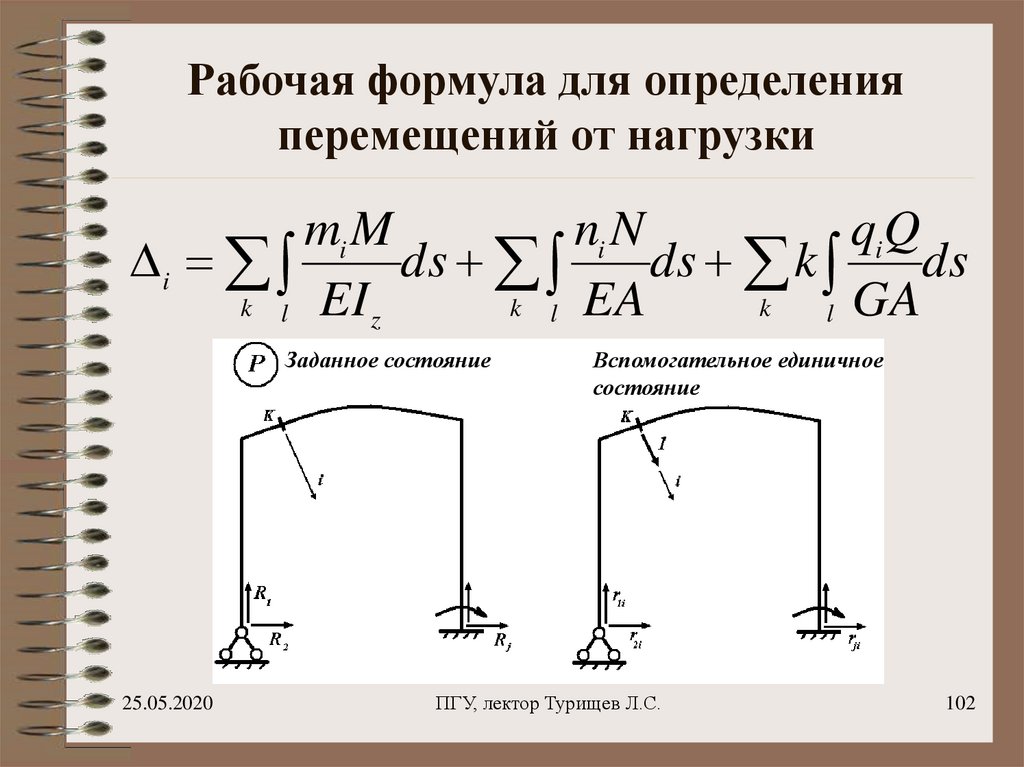
102. Рабочая формула для определения перемещений от нагрузки
mi Mni N
qiQ
i
ds
ds k
ds
k l EI z
k l EA
k
l GA
Заданное состояние
25.05.2020
Вспомогательное единичное
состояние
ПГУ, лектор Турищев Л.С.
102
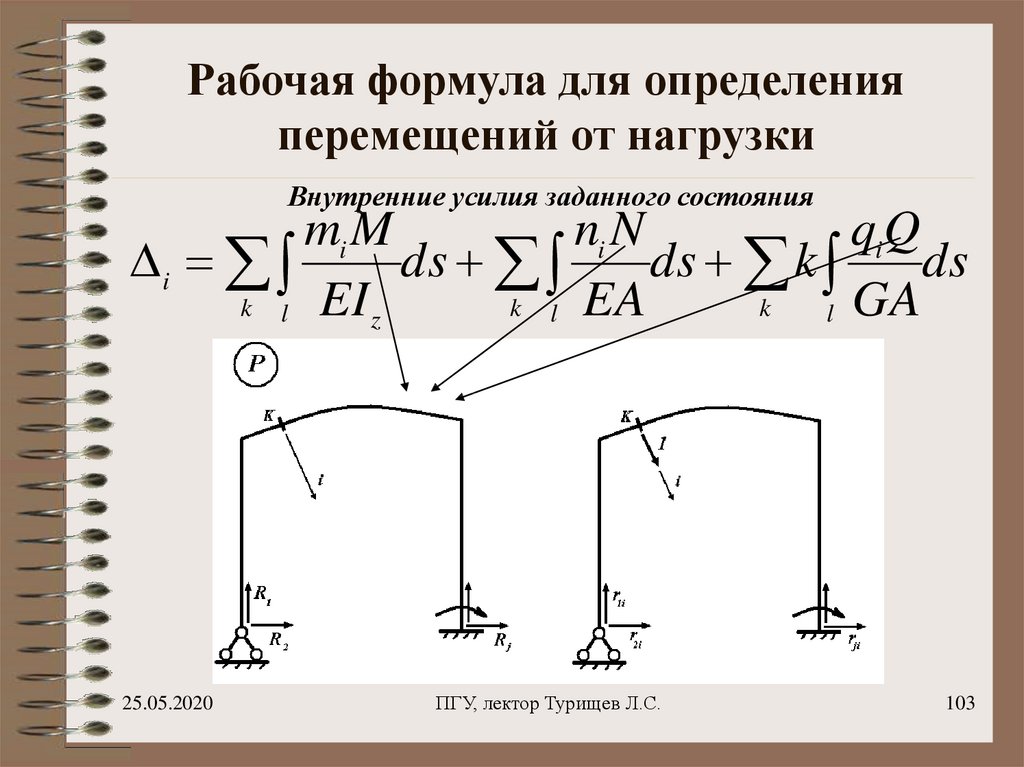
103. Рабочая формула для определения перемещений от нагрузки
Внутренние усилия заданного состоянияmi M
ni N
qiQ
i
ds
ds k
ds
k l EI z
k l EA
k
l GA
25.05.2020
ПГУ, лектор Турищев Л.С.
103
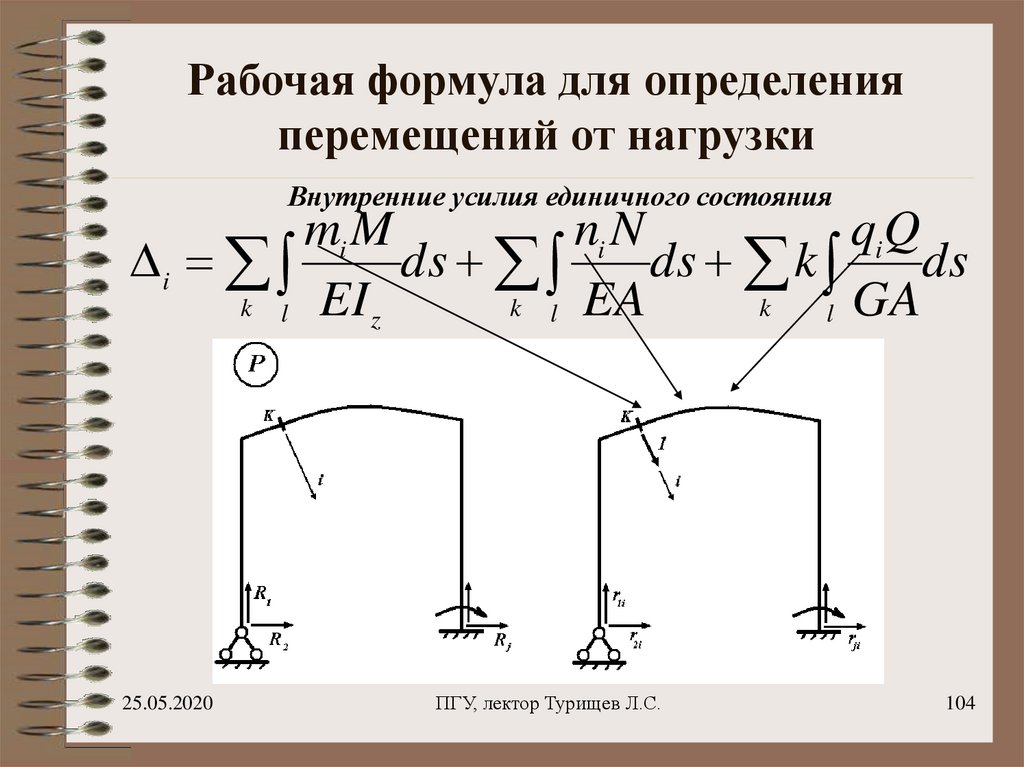
104. Рабочая формула для определения перемещений от нагрузки
Внутренние усилия единичного состоянияmi M
ni N
qiQ
i
ds
ds k
ds
k l EI z
k l EA
k
l GA
25.05.2020
ПГУ, лектор Турищев Л.С.
104
105. Рабочая формула для определения перемещений от нагрузки
mi Mni N
qiQ
i
ds
ds k
ds
k l EI z
k l EA
k
l GA
25.05.2020
ПГУ, лектор Турищев Л.С.
105
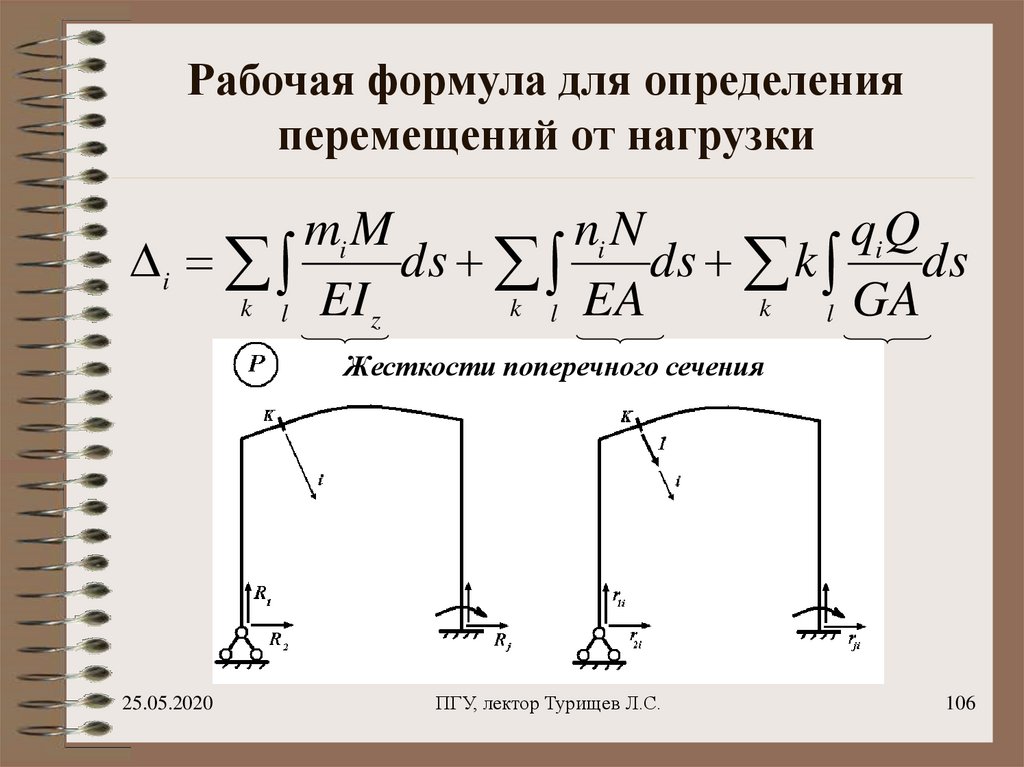
106. Рабочая формула для определения перемещений от нагрузки
mi Mni N
qiQ
i
ds
ds k
ds
k l EI z
k l EA
k
l GA
Жесткости поперечного сечения
25.05.2020
ПГУ, лектор Турищев Л.С.
106
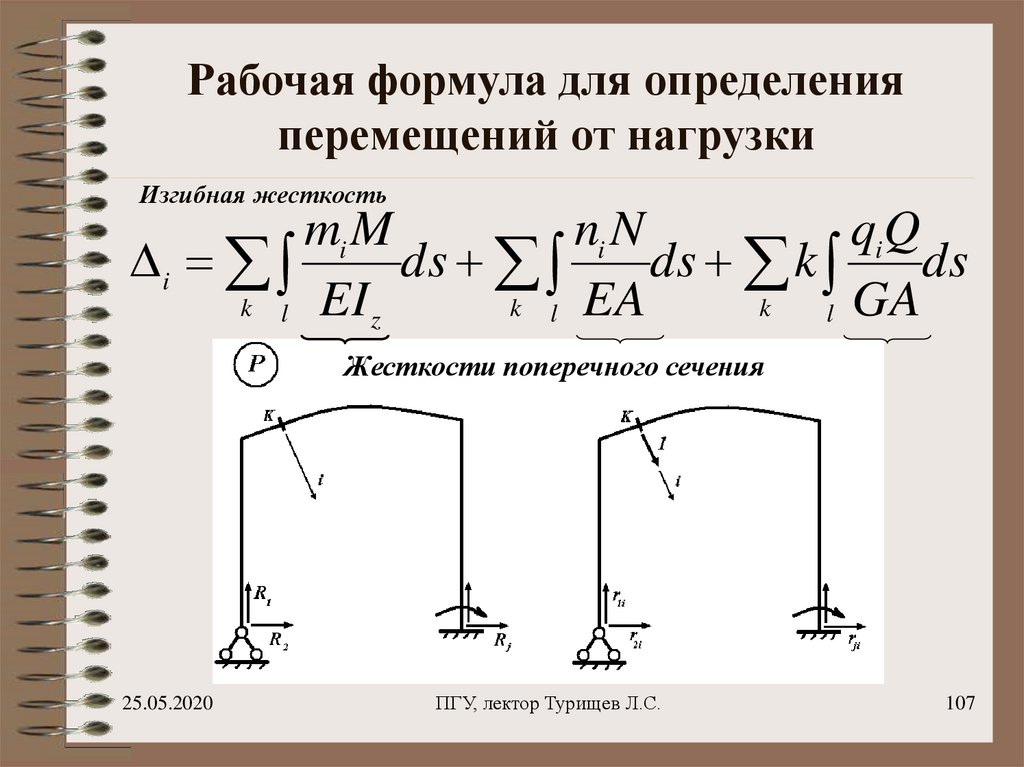
107. Рабочая формула для определения перемещений от нагрузки
Изгибная жесткостьmi M
ni N
qiQ
i
ds
ds k
ds
k l EI z
k l EA
k
l GA
Жесткости поперечного сечения
25.05.2020
ПГУ, лектор Турищев Л.С.
107
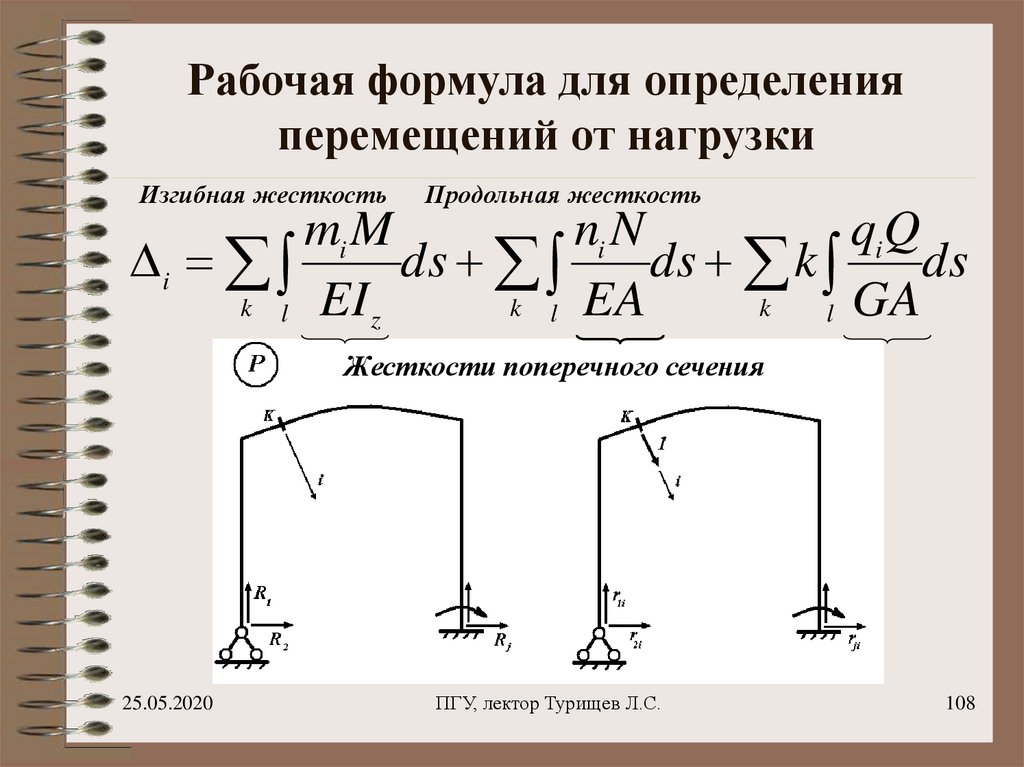
108. Рабочая формула для определения перемещений от нагрузки
Изгибная жесткостьПродольная жесткость
mi M
ni N
qiQ
i
ds
ds k
ds
k l EI z
k l EA
k
l GA
Жесткости поперечного сечения
25.05.2020
ПГУ, лектор Турищев Л.С.
108
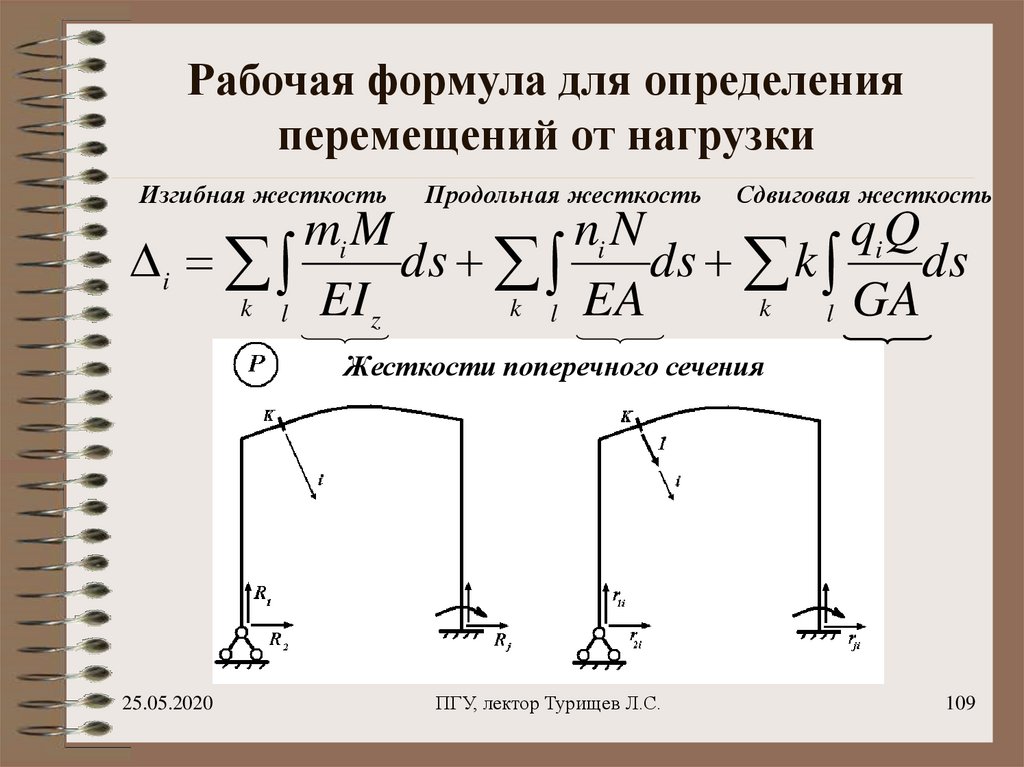
109. Рабочая формула для определения перемещений от нагрузки
Изгибная жесткостьПродольная жесткость
Сдвиговая жесткость
mi M
ni N
qiQ
i
ds
ds k
ds
k l EI z
k l EA
k
l GA
Жесткости поперечного сечения
25.05.2020
ПГУ, лектор Турищев Л.С.
109
110. Рабочая формула для определения перемещений от нагрузки для частных видов стержневых систем
Балки и рамные конструкции небольшойэтажности
mi M
i
ds
k l EI z
При определении перемещений можно учитывать
только изгибные деформации элементов конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
110
111. Рабочая формула для определения перемещений от нагрузки для частных видов стержневых систем
Рамные конструкции повышенной этажностиАрки и комбинированные системы
mi M
ni N
i
ds
ds
k l EI z
k l EA
При определении перемещений необходимо учитывать
изгибные и продольные деформации элементов конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
111
112. Рабочая формула для определения перемещений от нагрузки для частных видов стержневых систем
Ферменные конструкцииni N
i
ds
k l EA
При определении перемещений можно учитывать
только продольные деформации элементов конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
112
113. Рабочая формула для определения перемещений от нагрузки для частных видов стержневых систем
Ферменные конструкцииni N
ni N
i
ds
lk
k l EA
k EA
При определении перемещений можно учитывать
только продольные деформации элементов конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
113
114.
Какие есть вопросы?25.05.2020
ПГУ, лектор Турищев Л.С.
114
115.
Тогда идем дальше.25.05.2020
ПГУ, лектор Турищев Л.С.
115
116. 5.Особенности вычисления интегралов, встречающихся при определении перемещений
25.05.2020ПГУ, лектор Турищев Л.С.
116
117. Два типа поперечных сечений
• С переменнымиразмерами по длине
стержней конструкции
• С постоянными
размерами по длине
стержней конструкции
25.05.2020
ПГУ, лектор Турищев Л.С.
117
118. Поперечные сечения с переменными размерами
ik
l
mi M
nN
ds i ds k i ds
EI z
k l EA
k
l GA
Для вычисления интегралов,
входящих в формулу
Максвелла-Мора, применяют
методы численного интегрирования
25.05.2020
ПГУ, лектор Турищев Л.С.
118
119. Поперечные сечения с постоянными размерами
ik
l
mi M
nN
ds i ds k i ds
EI z
k l EA
k
l GA
25.05.2020
ПГУ, лектор Турищев Л.С.
119
120. Поперечные сечения с постоянными размерами
ik
l
mi M
nN
ds i ds k i ds
EI z
k l EA
k
l GA
EI z , EA, GA
Константы, независящие
от длин стержней
25.05.2020
ПГУ, лектор Турищев Л.С.
120
121. Поперечные сечения с постоянными размерами
ik
l
mi M
nN
ds i ds k i ds
EI z
k l EA
k
l GA
25.05.2020
m Mds, n Nds, q Qds
i
l
ПГУ, лектор Турищев Л.С.
i
l
i
l
121
122. Поперечные сечения с постоянными размерами
Внутренние усилия ед. состоянияi
k
l
mi M
nN
ds i ds k i ds
EI z
k l EA
k
l GA
m Mds, n Nds, q Qds
i
l
i
l
i
l
описываются по длине стержня
линейными функциями
25.05.2020
ПГУ, лектор Турищев Л.С.
122
123. Поперечные сечения с постоянными размерами
Внутренние усилия гр. состоянияi
k
l
mi M
nN
ds i ds k i ds
EI z
k l EA
k
l GA
m Mds, n Nds, q Qds
i
l
i
l
i
l
описываются по длине стержня
нелинейными функциями
25.05.2020
ПГУ, лектор Турищев Л.С.
123
124. Поперечные сечения с постоянными размерами
ik
l
mi M
nN
ds i ds k i ds
EI z
k l EA
k
l GA
m Mds, n Nds, q Qds
i
i
l
l
i
l
Линейные функции
mi , ni , qi
M , N, Q
Нелинейные функции
25.05.2020
ПГУ, лектор Турищев Л.С.
124
125. Поперечные сечения с постоянными размерами
ik
l
mi M
nN
ds i ds k i ds
EI z
k l EA
k
l GA
m Mds, n Nds, q Qds
i
i
l
l
i
l
xb
f
Fdx
xa
25.05.2020
ПГУ, лектор Турищев Л.С.
125
126. Поперечные сечения с постоянными размерами
ik
l
mi M
nN
ds i ds k i ds
EI z
k l EA
k
l GA
m Mds, n Nds, q Qds
i
i
l
l
i
l
Линейная функция
xb
f
Fdx
xa
Нелинейная функция
25.05.2020
ПГУ, лектор Турищев Л.С.
126
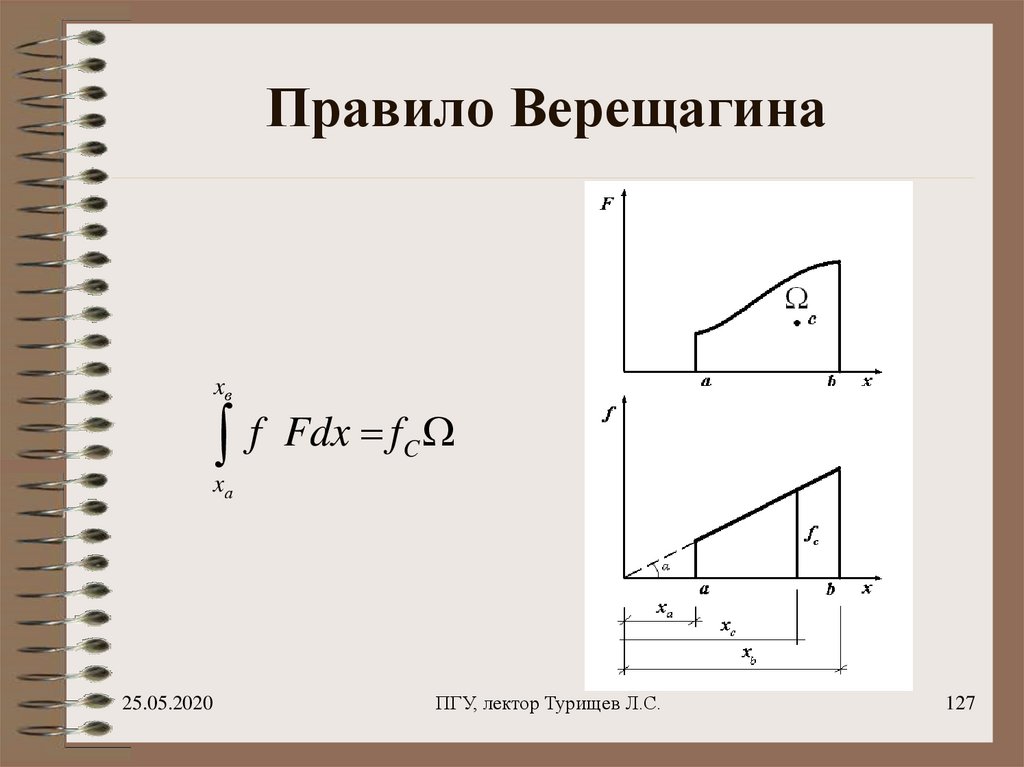
127. Правило Верещагина
xвf
Fdx f C
xа
25.05.2020
ПГУ, лектор Турищев Л.С.
127
128. Правило Верещагина
Определённый интеграл отпроизведения двух функций,
одна из которых линейная,
вторая нелинейная, равняется
произведению площади
xв
f
Fdx f C
xа
25.05.2020
ПГУ, лектор Турищев Л.С.
128
129. Правило Верещагина
Определённый интеграл отпроизведения двух функций,
одна из которых линейная,
вторая нелинейная, равняется
произведению площади
xв
f
Fdx f C
xа
графика нелинейной функции
25.05.2020
ПГУ, лектор Турищев Л.С.
129
130. Правило Верещагина
Определённый интеграл отпроизведения двух функций,
одна из которых линейная,
вторая нелинейная, равняется
произведению площади
xв
f
Fdx f C
xа
графика нелинейной функции
на ординату графика линейной
функции,
25.05.2020
ПГУ, лектор Турищев Л.С.
130
131. Правило Верещагина
Определённый интеграл отпроизведения двух функций,
одна из которых линейная,
вторая нелинейная, равняется
произведению площади
xв
f
Fdx f C
xа
графика нелинейной функции
на ординату графика линейной
функции,
взятую под центром тяжести
графика нелинейной функции
25.05.2020
ПГУ, лектор Турищев Л.С.
131
132. Правило Верещагина
(правило перемножения эпюр)Определённый интеграл от
произведения двух функций,
одна из которых линейная,
вторая нелинейная, равняется
произведению площади
xв
f
Fdx f C
xа
графика нелинейной функции
на ординату графика линейной
функции,
взятую под центром тяжести
графика нелинейной функции
25.05.2020
ПГУ, лектор Турищев Л.С.
132
133. Правило Верещагина
(правило перемножения эпюр)Определённый интеграл от
произведения двух функций,
одна из которых линейная,
вторая нелинейная, равняется
произведению площади
xв
f
xа
Fdx f C
графика нелинейной функции
на ординату графика линейной
функции,
взятую под центром тяжести
графика нелинейной функции
25.05.2020
Правило знаков
Если график нелинейной
функции
и ордината графика линейной
функции
расположены по одну сторону
от оси
то результат положительный
В противном случае он
отрицательный
ПГУ, лектор Турищев Л.С.
133
134. Границы применения правила Верещагина
25.05.2020ПГУ, лектор Турищев Л.С.
134
135. Границы применения правила Верещагина
25.05.2020ПГУ, лектор Турищев Л.С.
135
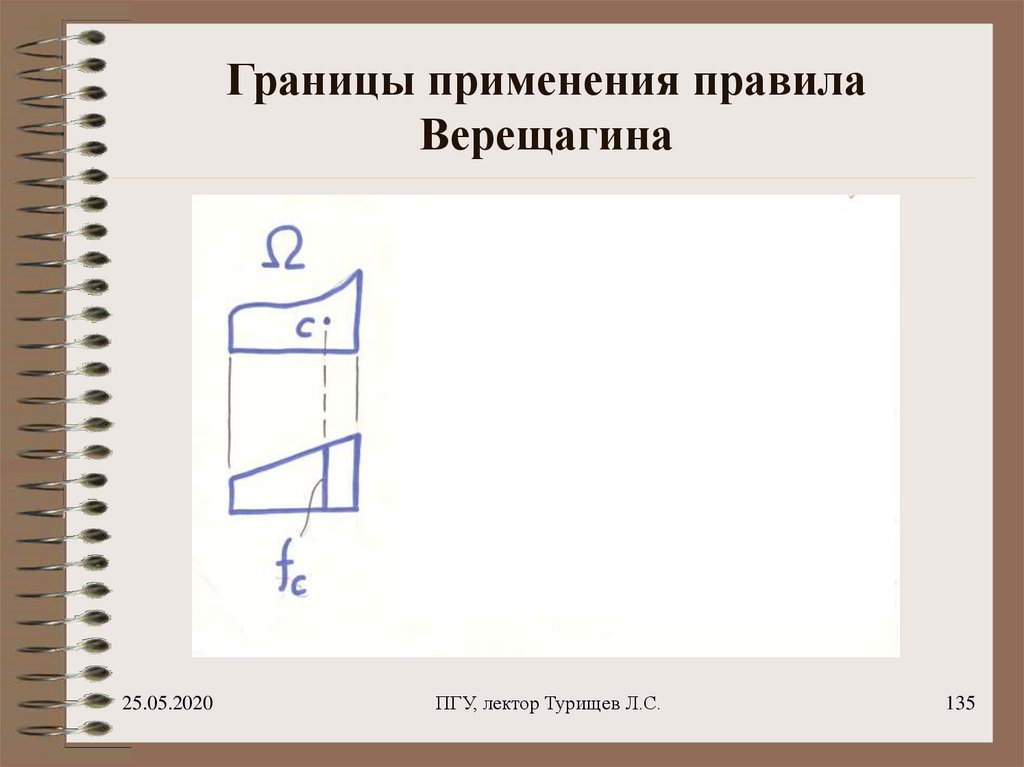
136. Границы применения правила Верещагина
25.05.2020ПГУ, лектор Турищев Л.С.
136
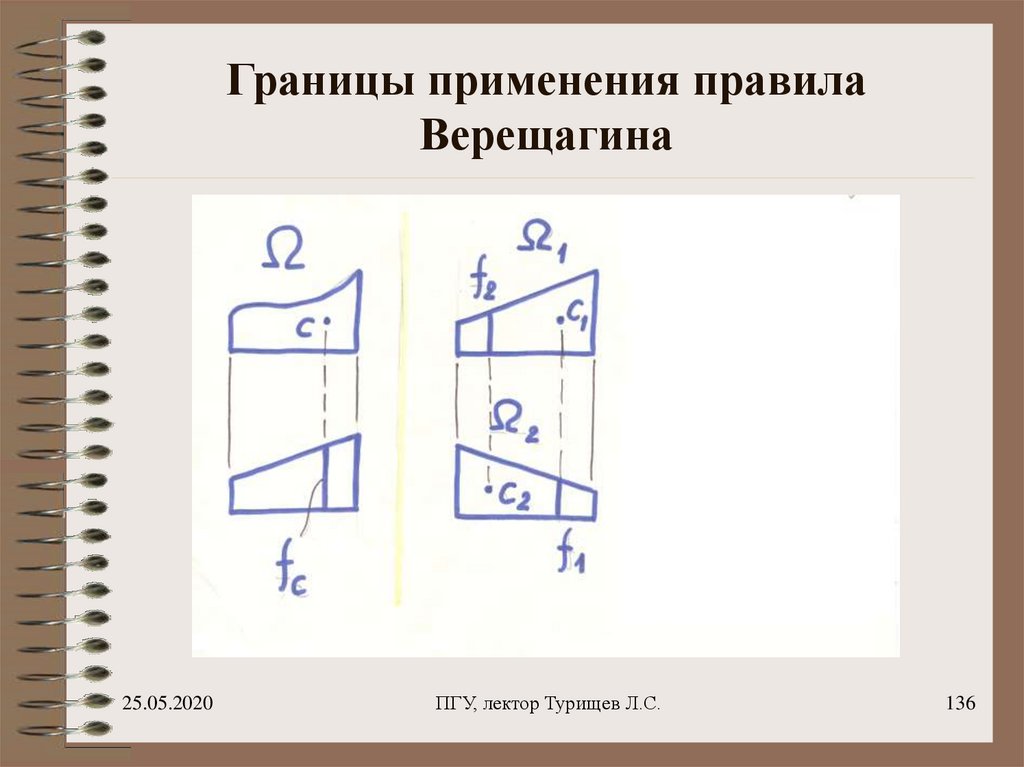
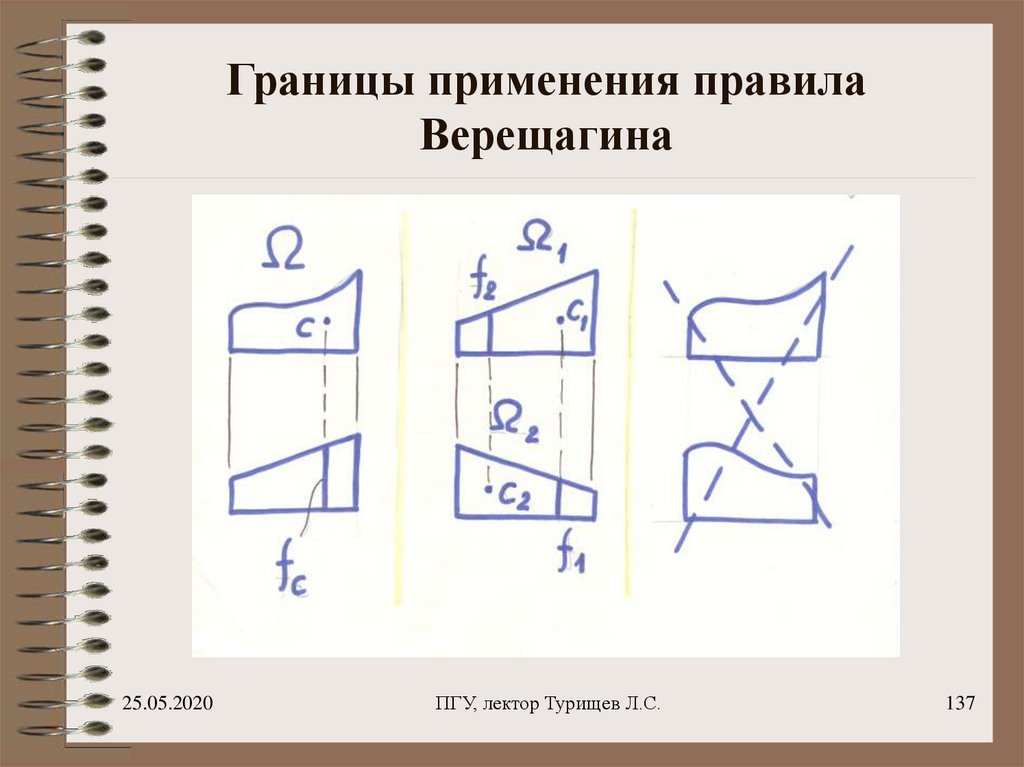
137. Границы применения правила Верещагина
25.05.2020ПГУ, лектор Турищев Л.С.
137
138.
Какие есть вопросы?25.05.2020
ПГУ, лектор Турищев Л.С.
138
139.
Совет от КонфуцияВчерашний день
учитель
сегодняшнего.
孔子
551 до н. э. — 479 до н. э.
25.05.2020
ПГУ, лектор Турищев Л.С.
139
140.
25.05.2020ПГУ, лектор Турищев Л.С.
140































































































 Механика
Механика








