Основы теории автоматического управления. Передаточные функции и уравнения замкнутой системы. Лекция 10

1. Лекция 10. Основы теории автоматического управления. Передаточные функции и уравнения замкнутой системы

1

2. Литература

2

3. Введение

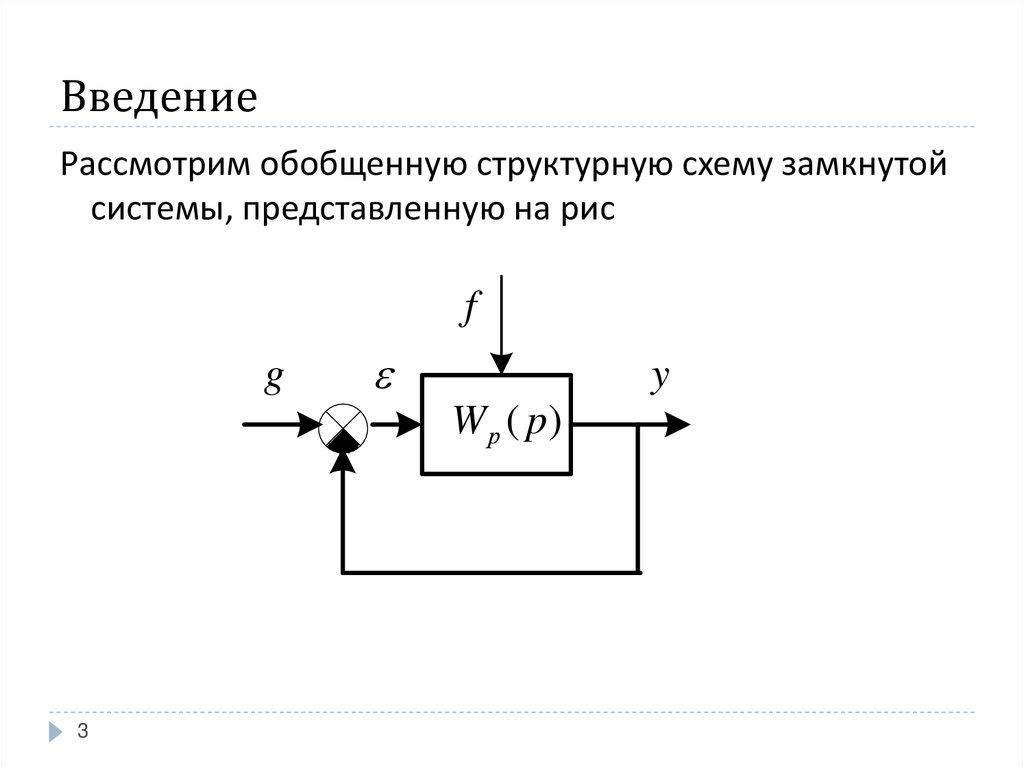
Рассмотрим обобщенную структурную схему замкнутой
системы, представленную на рис
f
g
y
W р ( p)
3

4. Введение

kB( p)
W р ( p)
A( p)
- передаточная функция разомкнутой цепи, в общем
случае сложная функция, полученная путем
преобразования,
k – коэффициент усиления разомкнутой части системы,
g (t ) – внешнее задающее воздействие,
f (t ) – возмущающее внешнее воздействие, как правило,
не одно и
(t ) – сигнал ошибки.
4

5. Введение

Отрицательная обратная связь между выходом и
входом, называется главной ООС.
Передаточные функции замкнутой системы
записывается отдельно для каждой комбинации
входа и выхода, то есть для каждой пары .
5

6. Введение

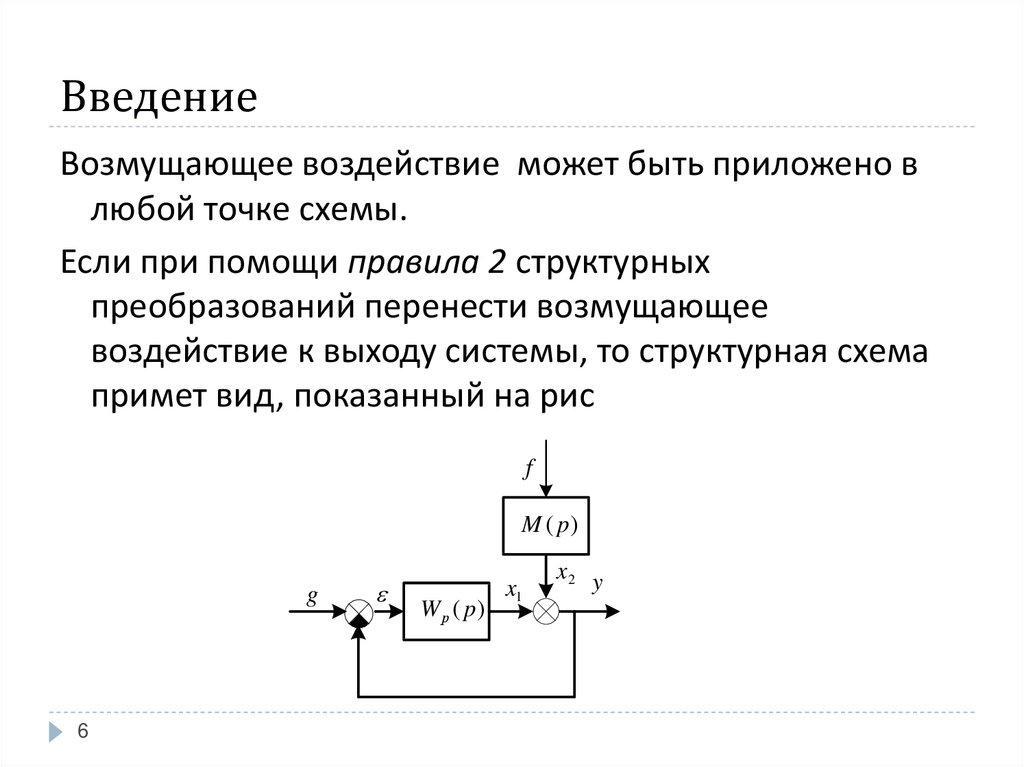
Возмущающее воздействие может быть приложено в
любой точке схемы.
Если при помощи правила 2 структурных
преобразований перенести возмущающее
воздействие к выходу системы, то структурная схема
примет вид, показанный на рис
f
M ( p)
g
6
W р ( p)
x1
x2 y

7. Введение

На выходе имеем условно y x1 x2
хотя на самом деле M ( p )
входит в общую схему как часть W p ( p )
7

8. Введение

Основные соотношения, описывающие динамику
системы, в изображениях по Лапласу будут иметь вид
( p) g ( p) y ( p)
y ( p) W р ( p) ( p) M ( p) f ( p)
8

9. Введение

В расчетах автоматических систем применяют три
основных вида передаточных функций замкнутой
системы.
1. Главная передаточная функция замкнутой системы,
которая определяется при условии f (t ) 0
y ( p)
( p) Wç ( p)
g ( p)
С учетом выражений имеем
y( p) Wp ( p) g ( p) y( p)
9

10. Введение

Откуда
Wð ( p)
kB( p )
( p)
1 W ð ( p) A( p) kB( p)
10

11. Введение

2. Передаточная функция замкнутой системы для
ошибки по задающему воздействию f (t ) 0
g ( p)
( p)
g ( p)
1 ( p)
1
kB( p)
A( p)
g ( p ) 1 ( p )
1
1 Wð ( p )
A( p) kB( p) A( p) kB( p)
11

12. Введение

3. Передаточная функция замкнутой системы по
возмущающему воздействию f (t ) определяется при
условии равенства нулю задающего воздействия g (t ) 0
f ( p)
y ( p)
f ( p)
Из формул при выполнении условия g (t ) 0 , следует
y ( p) Wp ( p) y ( p) M ( p) f ( p),
y ( p) 1 Wp ( p) M ( p) f ( p),
12

13. Введение

Откуда
M ( p)
R( p )
f ( p)
1 Wp ( p) A( p) kB( p)
4. Передаточная функция для ошибки по
возмущающему воздействию f ( p)
будет той же, что и для регулируемой величины , но с
обратным знаком f ( p)
f ( p )
13
( p)
f ( p)
f ( p)

14. Введение

Важно отметить, что знаменатель всех видов
передаточных функции замкнутой системы один и тот
же.
Для замкнутой системы в целом, зная передаточные
функции, можно перейти к дифференциальному
уравнению, представленному в изображениях по
Лапласу
y ( p) ( p) g ( p) f ( p) f ( p)
y ( p)
14
Wp ( p)
1 Wp ( p)
g ( p)
kB( p)
R( p)
g ( p)
f ( p).
A( p) kB( p)
A( p) kB( p)
M ( p)
f ( p),
1 Wp ( p)

15. Введение

Следовательно, дифференциальное уравнение
замкнутой системы имеет вид
A( p) kB( p) y( p) kB( p) g( p) R( p) f ( p)
Итак, зная передаточную функцию звеньев системы,
можно исключительно алгебраическим путем
определить общее дифференциальное уравнение
всей замкнутой системы в целом при любой её
сложности. Это является одним из основных
преимуществ использования аппарата передаточных
функций.
15

16. Введение

Характеристический полином замкнутой системы
имеет вид
D( p) A( p) kB( p) 0
Прядок дифференциального уравнения замкнутой
системы, как и разомкнутой цепи, определяется
степенью полинома A( p) , но коэффициенты
существенно отличаются за счет прибавления
многочлена kB( p) . Поэтому все динамические и
частотные свойства замкнутой САУ будут отличаться от
динамических и частотных свойств разомкнутой цепи,
состоящей из тех же звеньев.
16

17. Введение

В классической форме записи дифференциальное
уравнение, описывающее динамику САУ, можно
представить в виде
an y( n) a( n 1) y ( n)
a2 y a1 y a0 y bm g ( m)
b1 g b0 g r f ( r )
На основе передаточной функции по ошибке от
задающего воздействия и возмущающего
воздействия можно выразить ошибку, вернее
изображение ошибки, в виде
( p) g ( p) g ( p) f ( p) f ( p)
17
0 f (t )

18. Введение

Следовательно, дифференциальное уравнение для
ошибки в изображениях по Лапласу имеет вид
A( p) kB( p) ( p) A( p) g( p) R( p) f ( p)
Левая часть дифференциального уравнения, или
характеристическое уравнение для ошибки САУ, точно
такое же, что и для задающего воздействия. А вот
правая часть меняется существенно перед задающим
воздействием g (t ), хотя перед f (t ) возмущающим
воздействием изменился только знак.
18

19. Введение

Физический смысл рассмотренной динамической
модели таков: все изменения регулируемой
величины под влиянием возмущающего воздействия
сказываются целиком на ошибке системы.
19

20. Пример

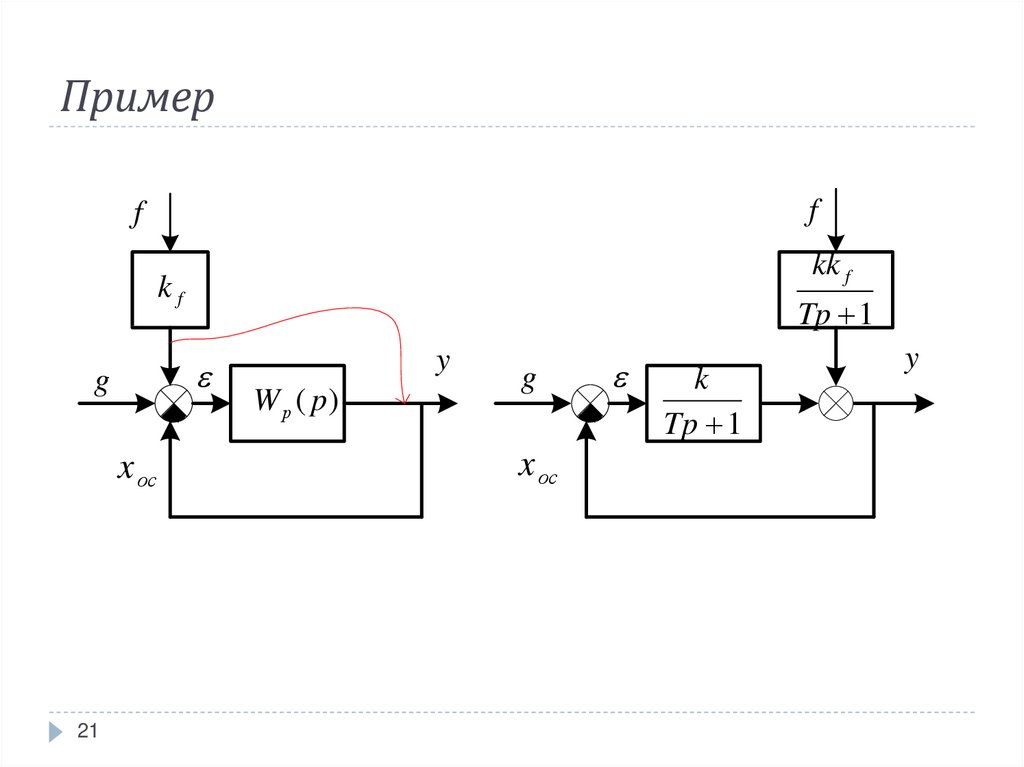
Пример вывода различных передаточных функций и
дифференциальных уравнений для САУ первого
порядка. На рис. приведены структурная схема САУ и
преобразованная структурная схема САУ, в которой
осуществлен перенос точки возмущающего
воздействия с входа системы на выход.
20

21. Пример

f
f
kk f
kf
g
x ос
21
Tp 1
y
W р ( p)
g
x ос
k
Tp 1
y

22. Пример

Главная передаточная функция САУ имеет вид
k
Wð ( p)
k
Tp 1
( p)
k
1 Wð ( p)
Tp (1 k )
1
Tp 1
Передаточная функция замкнутой системы для ошибки
по задающему воздействию
g ( p)
22
1
1 Wð ( p)
1
k
1
Tp 1
Tp 1
Tp (1 k )

23. Пример

Передаточная функция замкнутой системы по
возмущающему воздействию f (t ) определяется при
условии равенства нулю задающего воздействия g (t ) 0
и равна
kk f
kk f
M ( p)
Tp 1
f ( p)
k
1 Wp ( p)
Tp (1 k )
1
Tp 1
23

24. Пример

Передаточная функция для ошибки по возмущающему
воздействию f ( p) будет той же, что
передаточная функция замкнутой системы по
возмущающему воздействию f ( p) , но с
обратным знаком
f ( p )
24
kk f
Tp (1 k )

25. Пример

Дифференциальное уравнение замкнутой системы в
изображениях по Лапласу в классическом виде
kk f
k
y ( p ) ( p ) g ( p ) f ( p ) f ( p )
g ( p)
f ( p)
Tp (1 k )
Tp (1 k )
Tpy ( p) (1 k ) y ( p) kg( p) kk f f ( p)
Ty (1 k ) y (t ) kg(t ) kk f f (t )
25

26. Пример

Дифференциальное уравнение для ошибки в
изображениях по Лапласу и классическом виде
соответственно
kk f
Tp 1
( p)
g ( p)
f ( p)
Tp (1 k )
Tp (1 k )
Tp ( p) (1 k ) ( p) Tpg ( p) g ( p) kk f f ( p)
T (t ) (1 k ) (t ) Tg (t ) g (t ) kk f f (t )
Решив уравнения можно получить аналитическое
выражение переходных функций выходного сигнала
или сигнала ошибки.
26

27. Пример

Используя формулу главной передаточной функцией ( p )
можно определить выражение для АФЧХ замкнутой
системы посредством формальной замены оператора
в передаточной функции на j
( j )
W p ( j )
1 W p ( j )
W р ( j )
kB( j )
A( j )
представляет собой выражение амплитудно-фазовой
частотной характеристики разомкнутой цепи для
данной системы.
27