Производная функции

1. 25.05.20 Производная

функции

2.

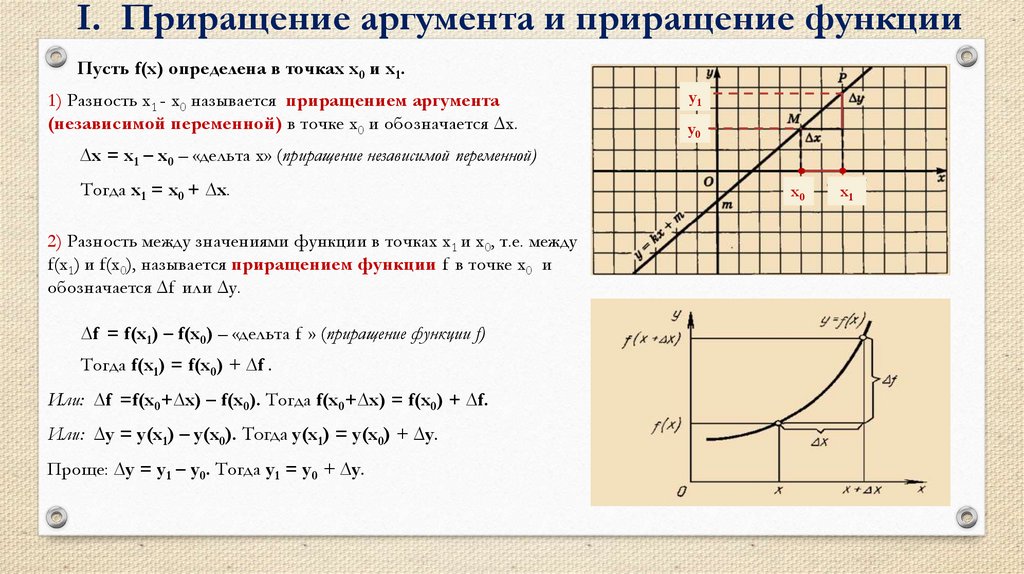
I. Приращение аргумента и приращение функции
Пусть f(х) определена в точках х0 и х1.
1) Разность х1 - х0 называется приращением аргумента
(независимой переменной) в точке х0 и обозначается ∆х.
у1
у0
∆х = х1 – х0 – «дельта х» (приращение независимой переменной)
Тогда х1 = х0 + ∆х.
2) Разность между значениями функции в точках х1 и х0, т.е. между
f(х1) и f(х0), называется приращением функции f в точке x0 и
обозначается ∆f или ∆у.
∆f = f(х1) – f(х0) – «дельта f » (приращение функции f)
Тогда f(х1) = f(х0) + ∆f .
Или: ∆f =f(х0+∆х) – f(х0). Тогда f(х0+∆х) = f(х0) + ∆f.
Или: ∆у = у(х1) – у(х0). Тогда у(х1) = у(х0) + ∆у.
Проще: ∆у = у1 – у0. Тогда у1 = у0 + ∆у.
х0
х1

3.

I. Приращение аргумента и приращение функции
3) Основные формулы
∆х = х1 – х0
∆f = f(х1) – f(х0)
∆f =f(х0+∆х) – f(х0)
∆у = у1 – у0
х1 = х0 + ∆х
f(х1) = f(х0) + ∆f
f(х0+∆х) = f(х0) + ∆f
у1 = у0 + ∆у
Примеры.
1. Дано: у = х2 – 1, х0 = 0, х1 = 0,1.
Найти: приращения аргумента и функции.
Решение:
1) ∆х = х1 – х0
∆х = 0,1 – 0 = 0,1
2) ∆у = у(х1) – у(х0 )
∆у = (0,12 – 1) – (02 – 1)= 0,01 – 1 + 1 = 0,01
2. Дано: у = х2 – 1, х → х+∆х.
Найти: приращение функции (∆у).
Решение:
1) ∆у = у1 – у0 = у(х+∆х) – у(х )
Это подстановка в формулу функции.
∆у = ( (х+∆х)2 – 1) – (х2 – 1) = х2 + 2х∆х + (∆х)2 –
– 1 – х2 + 1 = 2х∆х + (∆х)2 = ∆х(2х + ∆х)

4.

I. Приращение аргумента и приращение функции
3) Основные формулы
∆х = х1 – х0
∆f = f(х1) – f(х0)
∆f =f(х0+∆х) – f(х0)
∆у = у1 – у0
х1 = х0 + ∆х
f(х1) = f(х0) + ∆f
f(х0+∆х) = f(х0) + ∆f
у1 = у0 + ∆у
Примеры.
3. Дано: у = х3 , х → х+∆х.
Найти: ∆у.
4. Дано: у = kx + b, х → х+∆х.
Найти: ∆у.
Решение:
Решение:
1) ∆у = у1 – у0 = у(х+∆х) – у(х )
1) ∆у = у1 – у0 = у(х+∆х) – у(х )
Это подстановка в формулу функции.
∆у = ( k(х+∆х)+ b ) – (kх + b) = kх + k∆х + b – kх -
∆у = (х+∆х)3 – х3 = х3 + 3х2∆х + 3х∆х2 +∆х3 – х3 =
- b = k∆х
= 3х2∆х + 3х∆х2 +∆х3 = ∆х(3х2 + 3х∆х +∆х2 )

5.

I. Приращение аргумента и приращение функции
3) Основные формулы
∆х = х1 – х0
∆f = f(х1) – f(х0)
∆f =f(х0+∆х) – f(х0)
∆у = у1 – у0
х1 = х0 + ∆х
f(х1) = f(х0) + ∆f
f(х0+∆х) = f(х0) + ∆f
у1 = у0 + ∆у
Примеры.
5. Дано: у = х3 , х → х+∆х.
∆у
Найти: отношение ∆х.
6. Дано: у = kx + b, х → х+∆х.
∆у
Найти: отношение ∆х.
Решение:
Решение:
1) Найдем ∆у (воспользуемся примером 3).
1) Найдем ∆у (воспользуемся примером 4).
∆у = ∆х(3х2 + 3х∆х +∆х2 )
∆у = k∆х
∆у ∆х(3х2 + 3х∆х +∆х2 )
2 + 3х∆х +∆х2
2) ∆х =
=
3х
∆х
∆у k∆х
2) ∆х = ∆х = k.

6.

I. Приращение аргумента и приращение функции
3) Основные формулы
∆х = х1 – х0
∆f = f(х1) – f(х0)
∆f =f(х0+∆х) – f(х0)
∆у = у1 – у0
х1 = х0 + ∆х
f(х1) = f(х0) + ∆f
f(х0+∆х) = f(х0) + ∆f
у1 = у0 + ∆у
Примеры.
7. Дано: у = ах2 , х → х+∆х.
∆у
Найти: отношение ∆х.
Решение:
1) Найдем ∆у:
∆у = у1 – у0 = у(х+∆х) – у(х )
∆у = а(х+∆х)2 – ах2 = ах2 + 2ах∆х + а(∆х)2 – ах2 =
= 2ах∆х +
а(∆х)2 =
а∆х(2х + ∆х)
∆у а∆х(2х + ∆х)
2) ∆х =
= а(2х + ∆х)
∆х
Дальнейшая мысль:
Если ∆х → 0, то а(2х + ∆х) → 2ах.
Из примера 5:
Если ∆х → 0, то 3х2 + 3х∆х +∆х2 → 3х2
…. и т.д.