Похожие презентации:
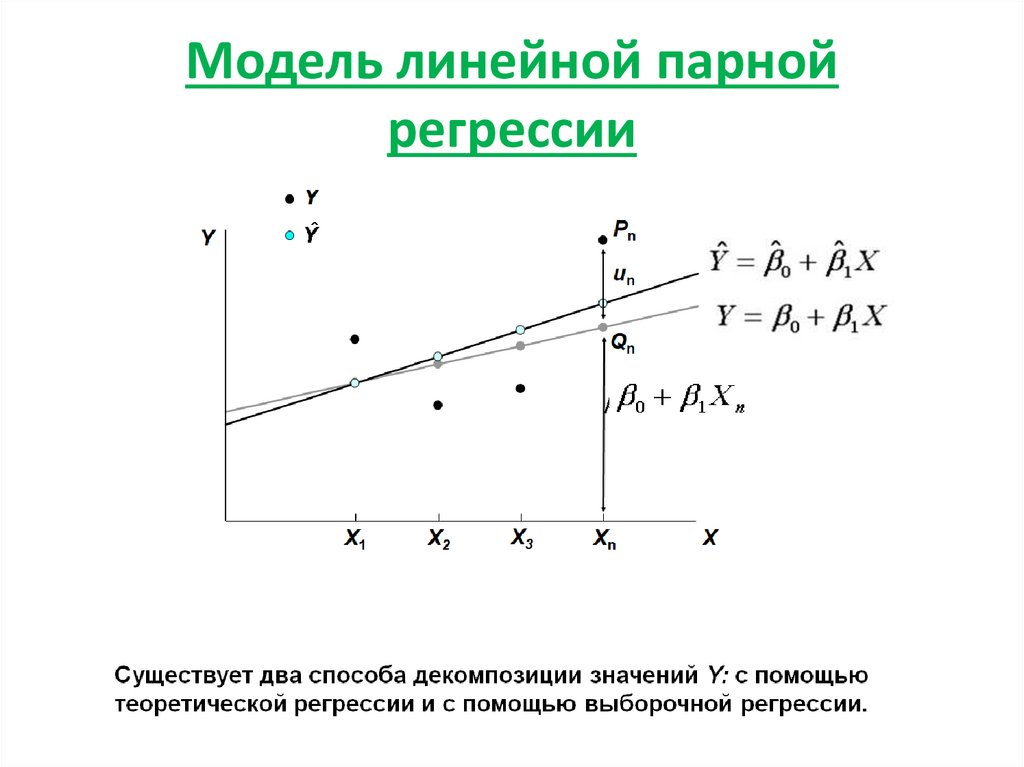
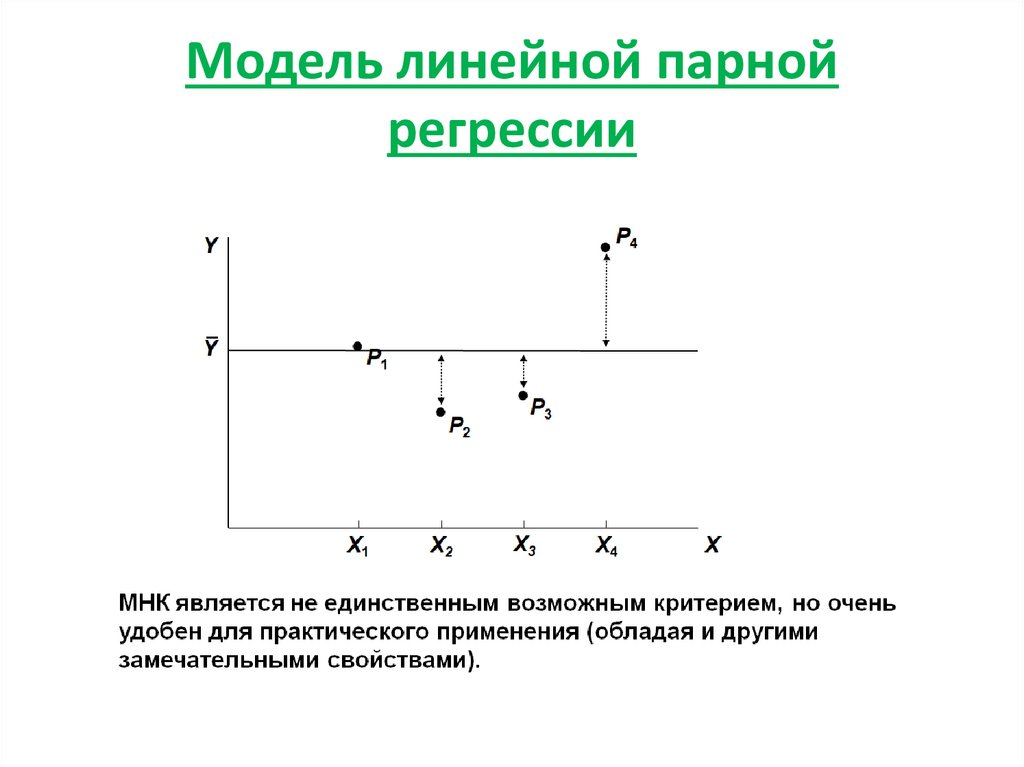
Модель линейной парной регрессии
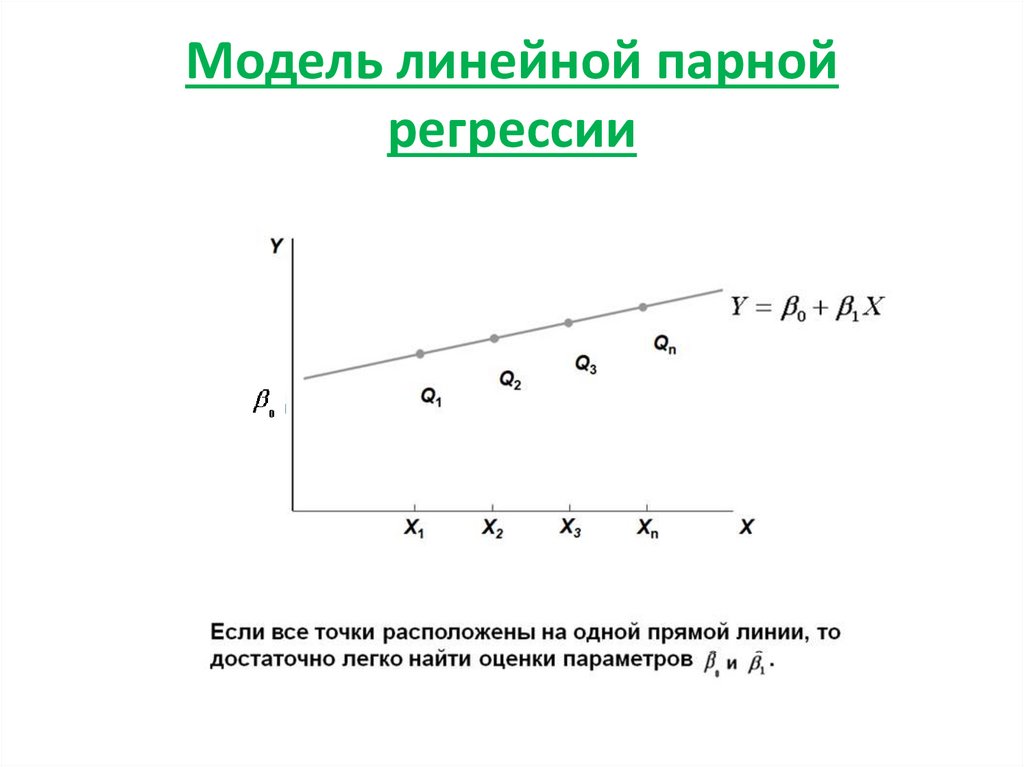
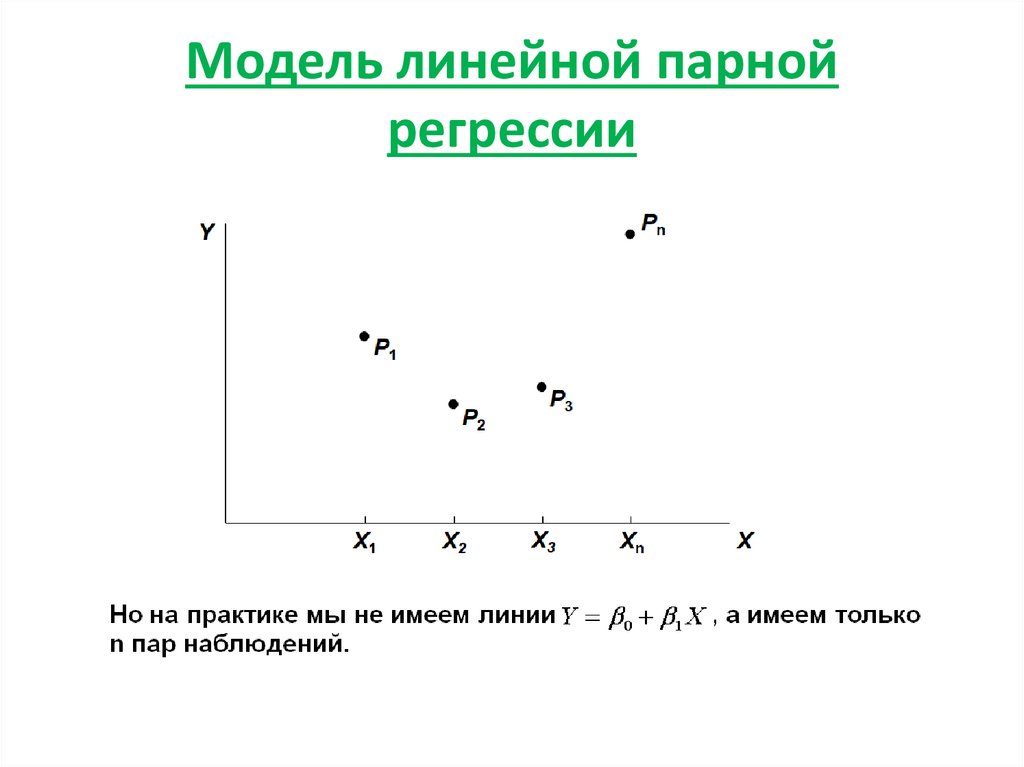
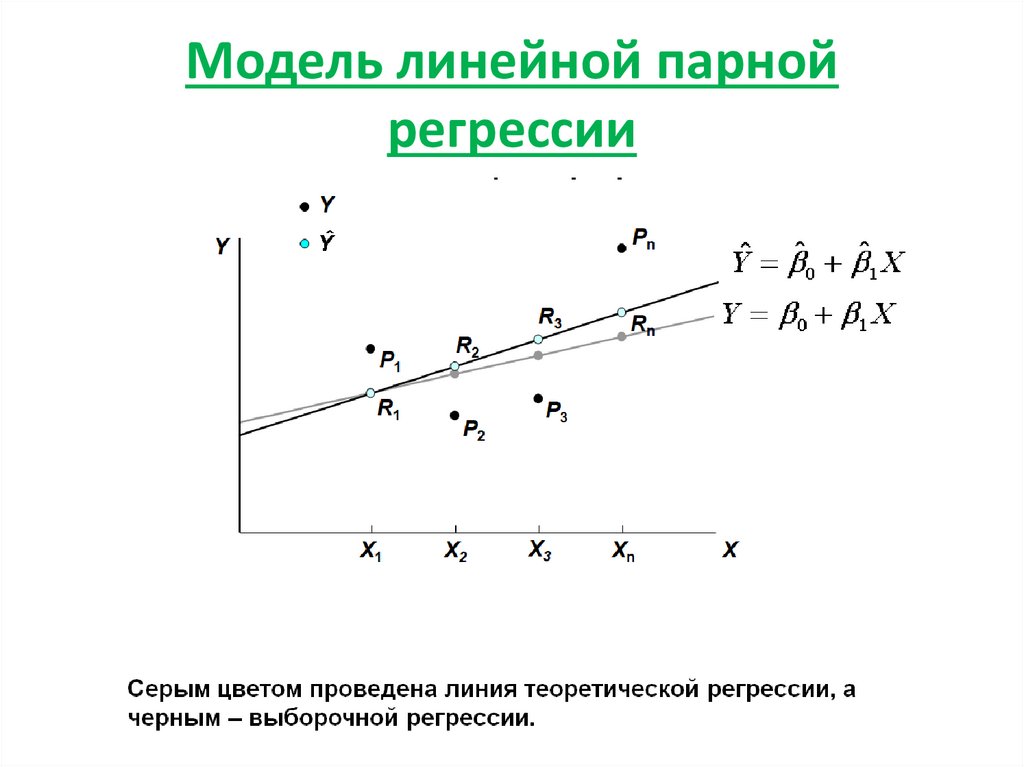
1. Модель линейной парной регрессии
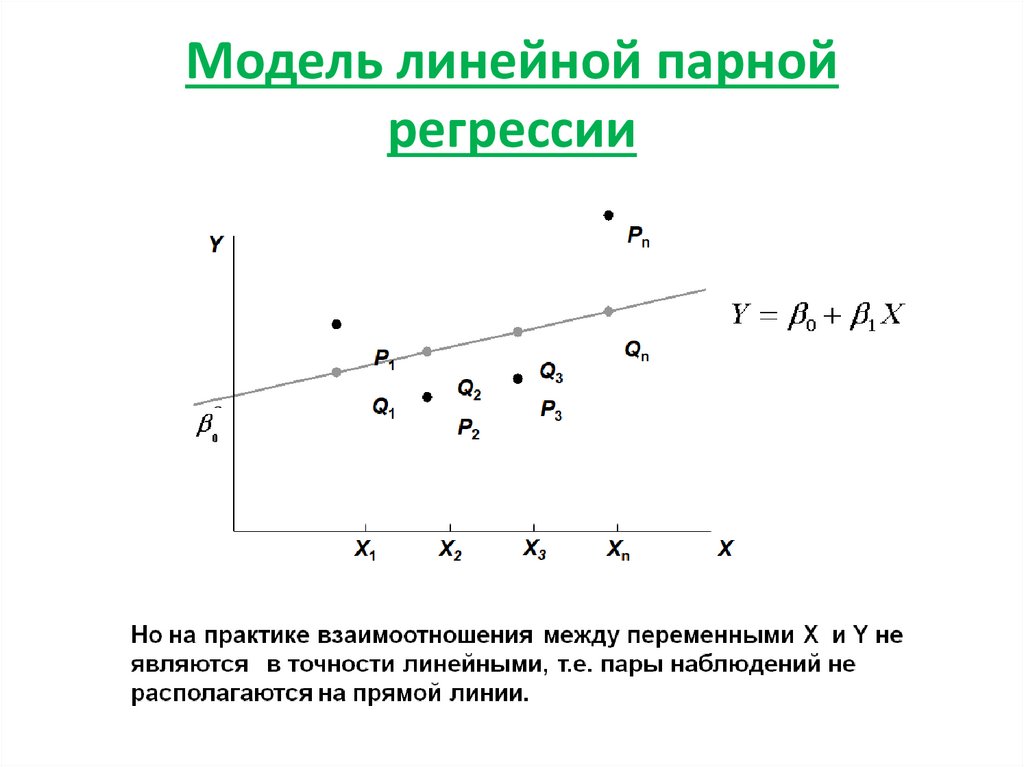
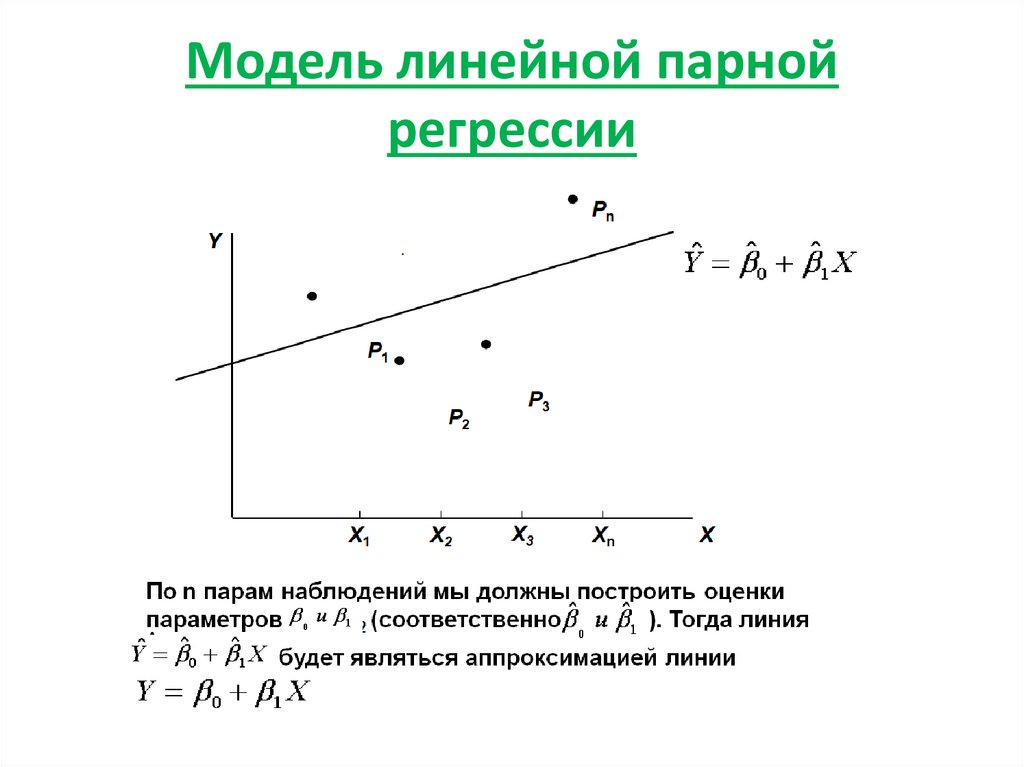
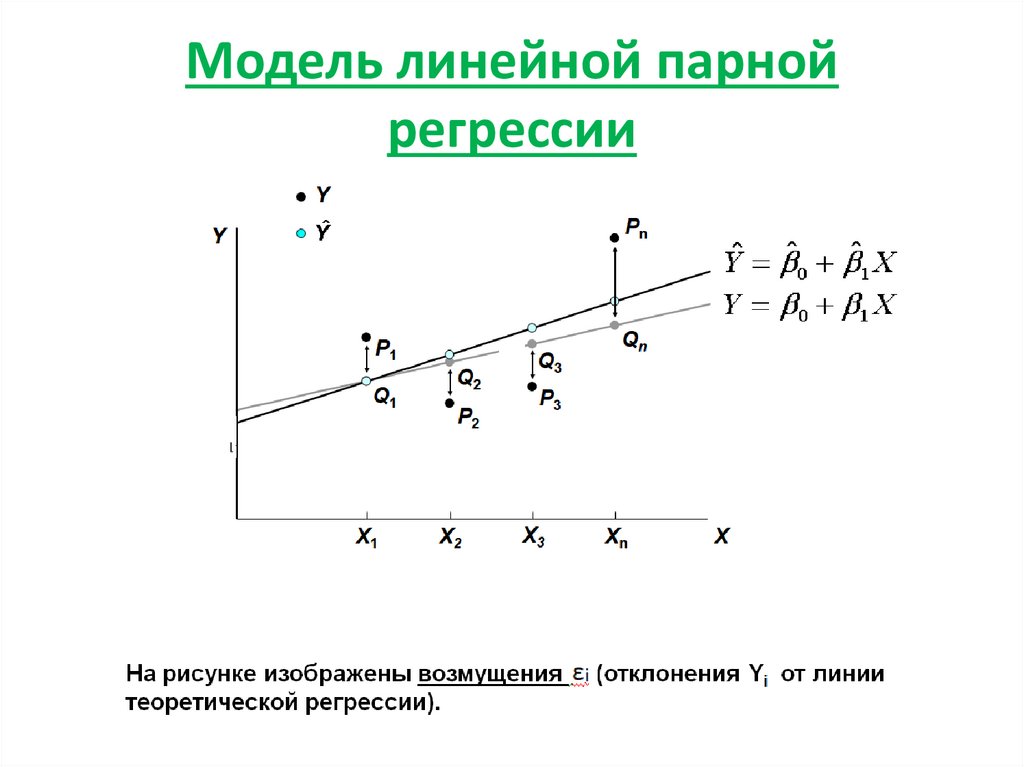
2. Модель линейной парной регрессии
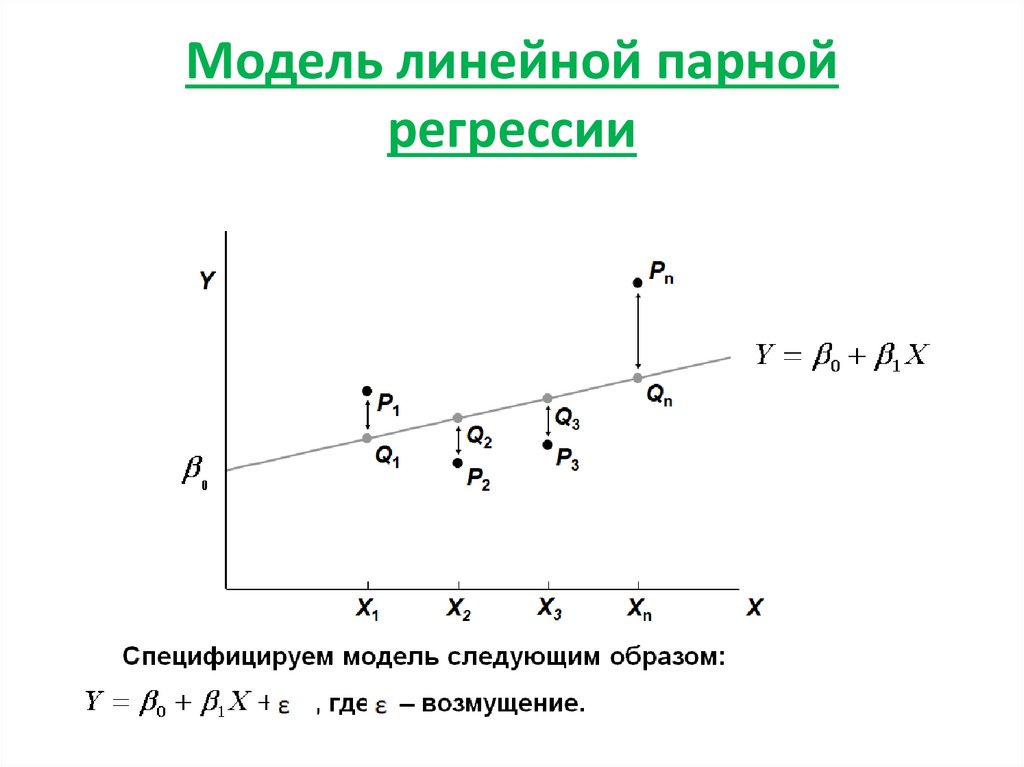
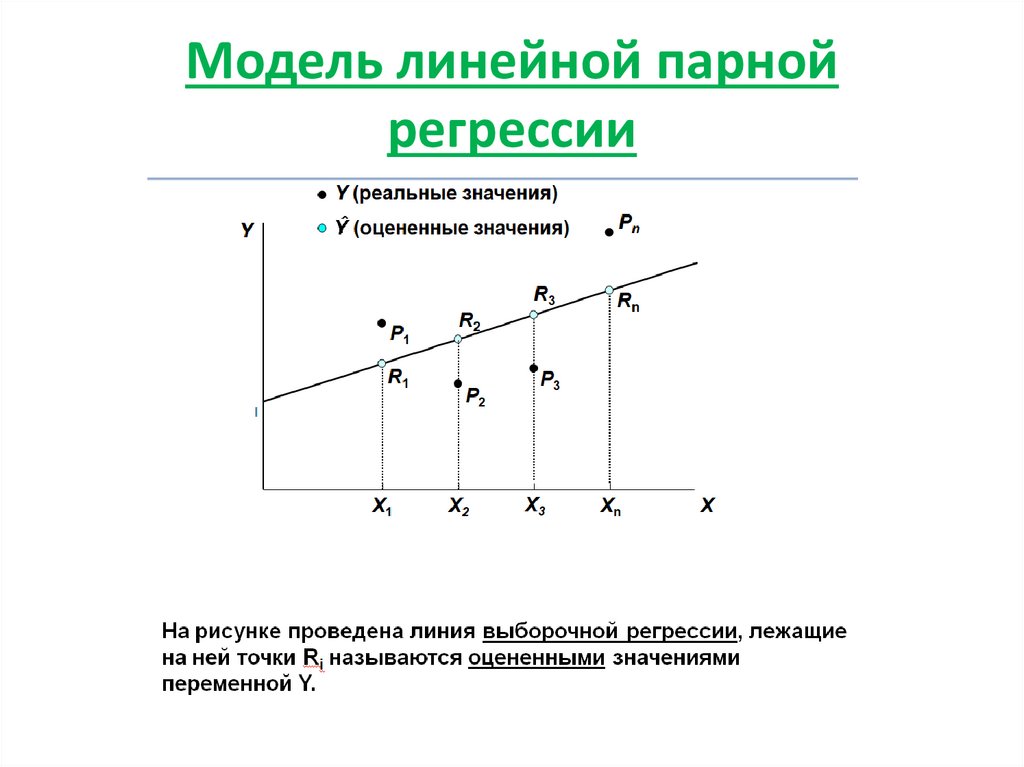
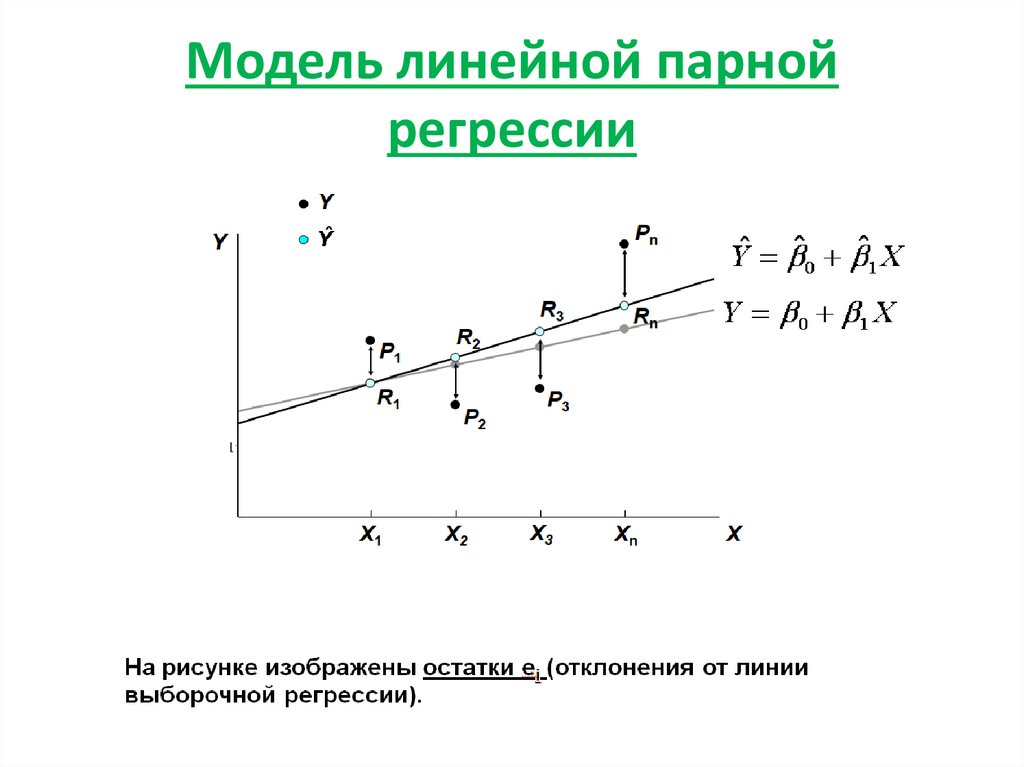
3. Модель линейной парной регрессии
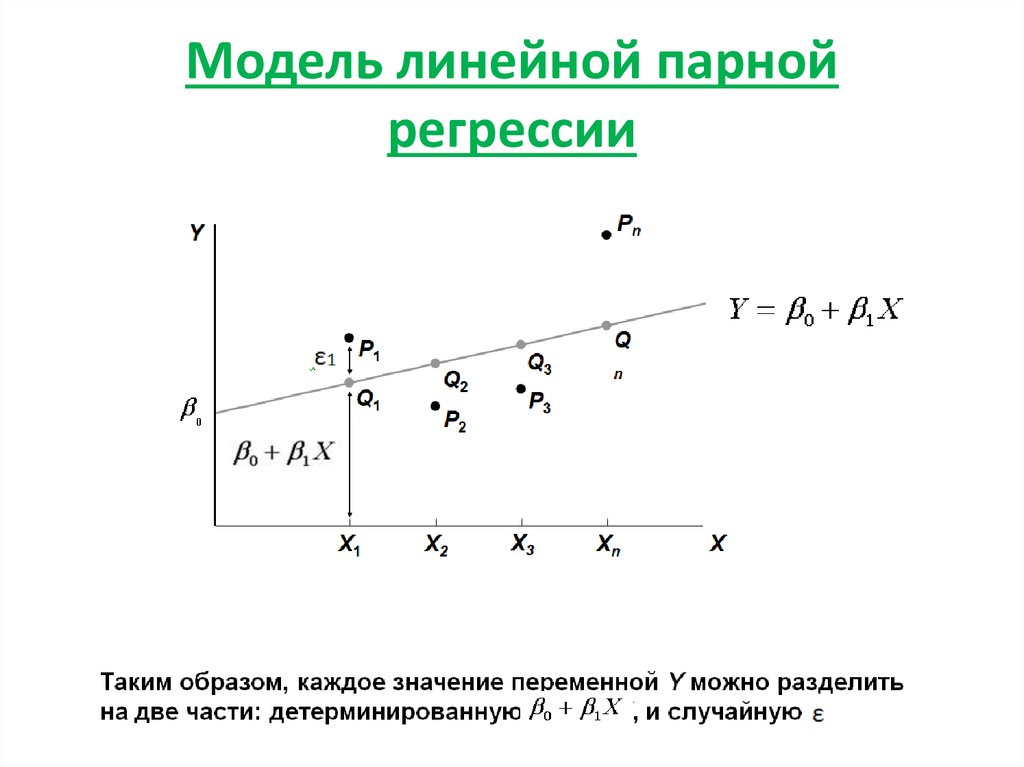
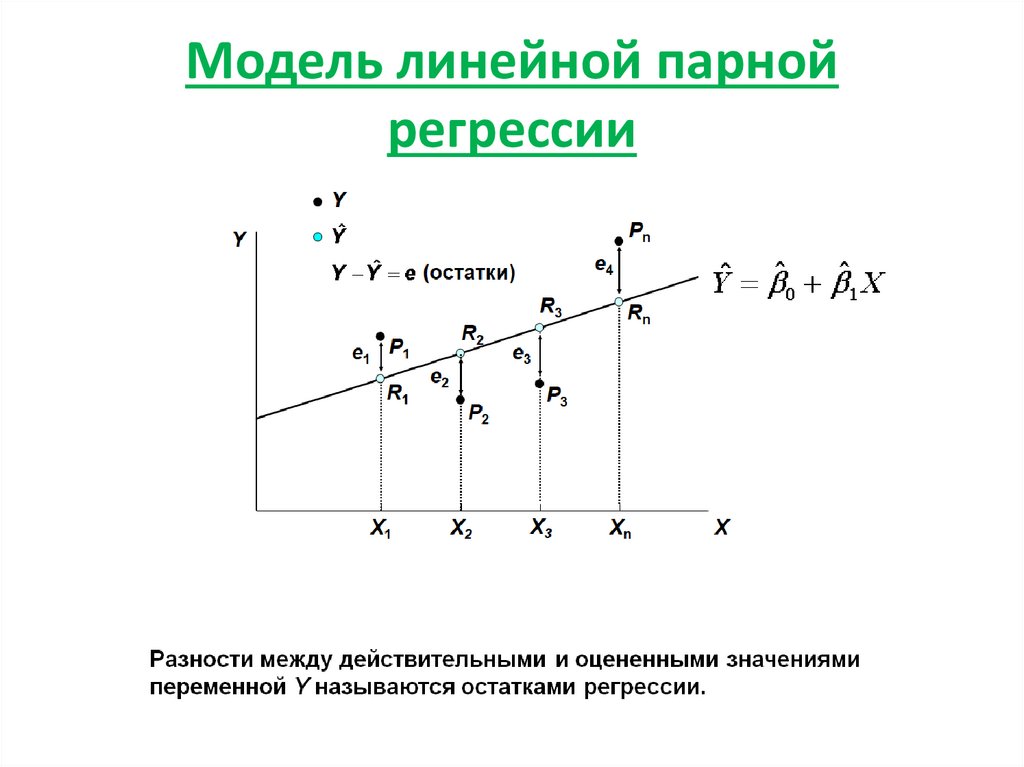
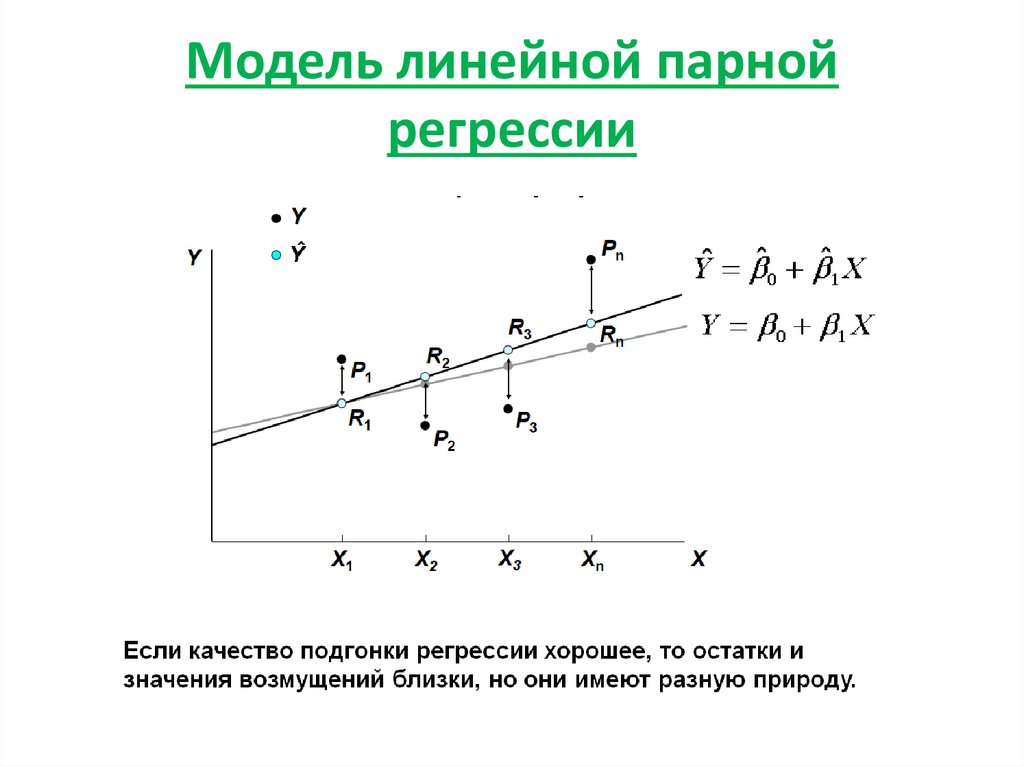
4. Модель линейной парной регрессии
5. Модель линейной парной регрессии
6. Модель линейной парной регрессии
7. Модель линейной парной регрессии
8. Модель линейной парной регрессии
9. Модель линейной парной регрессии
10. Модель линейной парной регрессии
11. Модель линейной парной регрессии
12. Модель линейной парной регрессии
13. Модель линейной парной регрессии
14. Модель линейной парной регрессии
15. Модель линейной парной регрессии
16. Модель линейной парной регрессии
17. Модель линейной парной регрессии
18. Модель линейной парной регрессии
19. Модель линейной парной регрессии
20. Модель линейной парной регрессии
21. Модель линейной парной регрессии
22. Модель линейной парной регрессии
• Вывод формул для нахождениякоэффициентов регрессии – доска
• Формулы для нахождения коэффициентов
регрессии
23. Модель линейной парной регрессии
24. Модель линейной парной регрессии
25. Модель линейной парной регрессии
26. Модель линейной парной регрессии
Интерпретация коэффициента при переменной х
Дисперсионный анализ, коэффициент детерминации
Теорема Гаусса-Маркова для случая парной регрессии
Формулы для нахождения дисперсии МНК-оценок
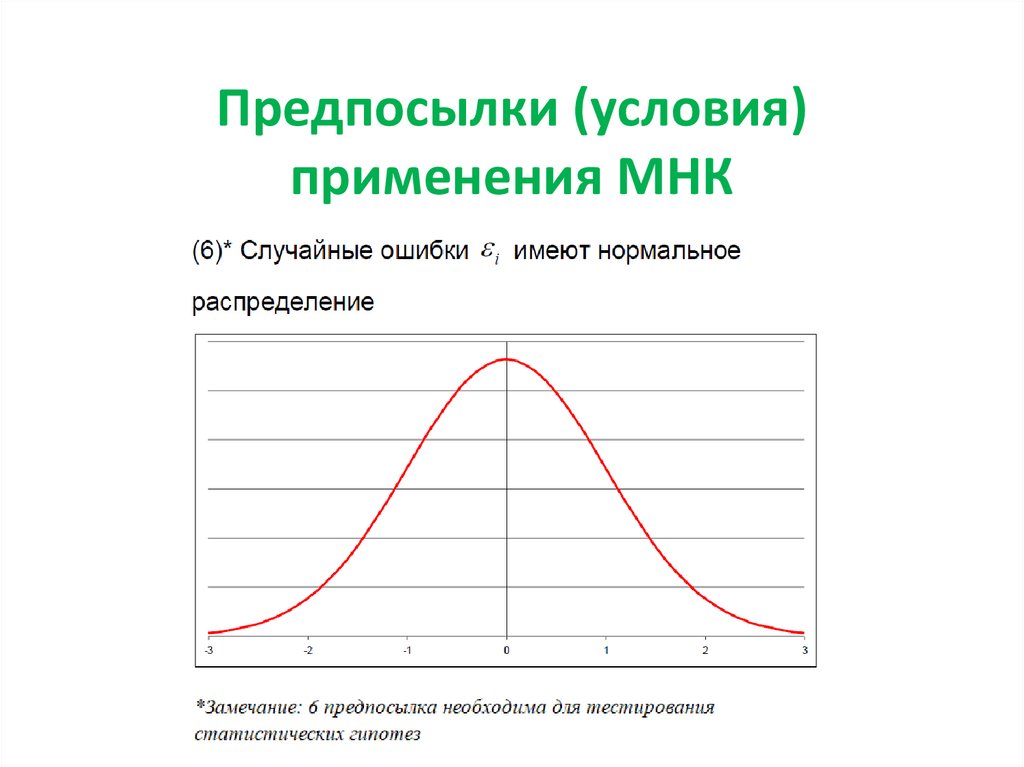
Предположение о нормальном распределении
случайной ошибки
Тестирование гипотезы о конкретном значении
коэффициента регрессии
Проверка значимости коэффициента при переменной х
Если коэффициент незначим, его не интерпретируют!!!!
Значимость константы обычно не проверяется
Доверительный интервал для коэффициента регрессии
27. Интерпретация коэффициента регрессии
• Коэффициентпри
переменной
Х
показывает, на сколько единиц в среднем
изменится У, если значение Х увеличится
на 1 единицу (следует из определения
производной).
• Свободный член в уравнении регрессии –
это значение переменной Y при Х = 0.
28. Остатки регрессии
29. Дисперсионный анализ
30. Дисперсионный анализ
31. Коэффициент детерминации
32. Коэффициент детерминации
33. Коэффициент детерминации
34. Коэффициент детерминации
35. Расчет коэффициента детерминации
36. Расчет коэффициента детерминации
37. Предпосылки (условия) применения МНК
38. Предпосылки (условия) применения МНК
39. Предпосылки (условия) применения МНК
40. Предпосылки (условия) применения МНК
41. Предпосылки (условия) применения МНК
42. Предпосылки (условия) применения МНК
43. Предпосылки (условия) применения МНК
44. Предпосылки (условия) применения МНК
45. Теорема Гаусса-Маркова для случая парной регрессии
Теорема: Если предпосылки 1-5 выполнены,то оценки, полученные МНК являются BLUE
(Best Linear Unbased Estimators) –
наилучшими линейными несмещенными
оценками и они обладают следующими
свойствами:
46. Теорема Гаусса-Маркова для случая парной регрессии
1. Оценки являются несмещенными, т.е.E ( ) = β0, E ( ) = β1. Это вытекает из того,
что E(ξ)=0, тогда говорят об отсутствии
систематической ошибки в определении
положения линии регрессии
47. Теорема Гаусса-Маркова для случая парной регрессии
2. Оценки состоятельны, т.к. дисперсия оценокпараметров при возрастании числа n наблюдений
стремится к нулю:
Т.е. при увеличении объема выборки надежность
оценок увеличивается
3. Оценки эффективны, т.е. они имеют наименьшую
дисперсию по сравнению с любыми другими
оценками
данных
параметров,
линейными
относительно величин У.
48.
49.
Утверждение: Если выполнены условия теоремыГаусса-Маркова, то дисперсии МНК-оценок могут
быть найдены по следующим формулам:
50.
51. Стандартные ошибки для оценок коэффициентов линейной парной регрессии
52. Проверка гипотез о конкретном значении коэффициентов парной регрессии
53. Выбор тестовой статистики
• Используются соображения: если гипотезане отвергается, то
Тогда статистика
имеет
распределение N (0; 1). НО!!!!!
В выражение для
входит
неизвестный параметр
(см.формулу).
Поэтому вычислить эту статистику невозможно.
54. Выбор тестовой статистики
Поэтому заменим неизвестный параметрего оценкой
, но в этом случае
распределение статистики для случайной
величины
уже не будет нормальным.
Тестовая статистика
имеет
распределение Стьюдента с (n-2) степенями
свободы.
55. Тестирование гипотезы о равенстве коэффициента регрессии конкретному значению
• 1.а). Вычисляем значение тестовой статистики
б). Сравниваем
.. Если
то Н0 отвергается в пользу Н1.
,
56. Тестирование гипотезы о равенстве коэффициента регрессии конкретному значению
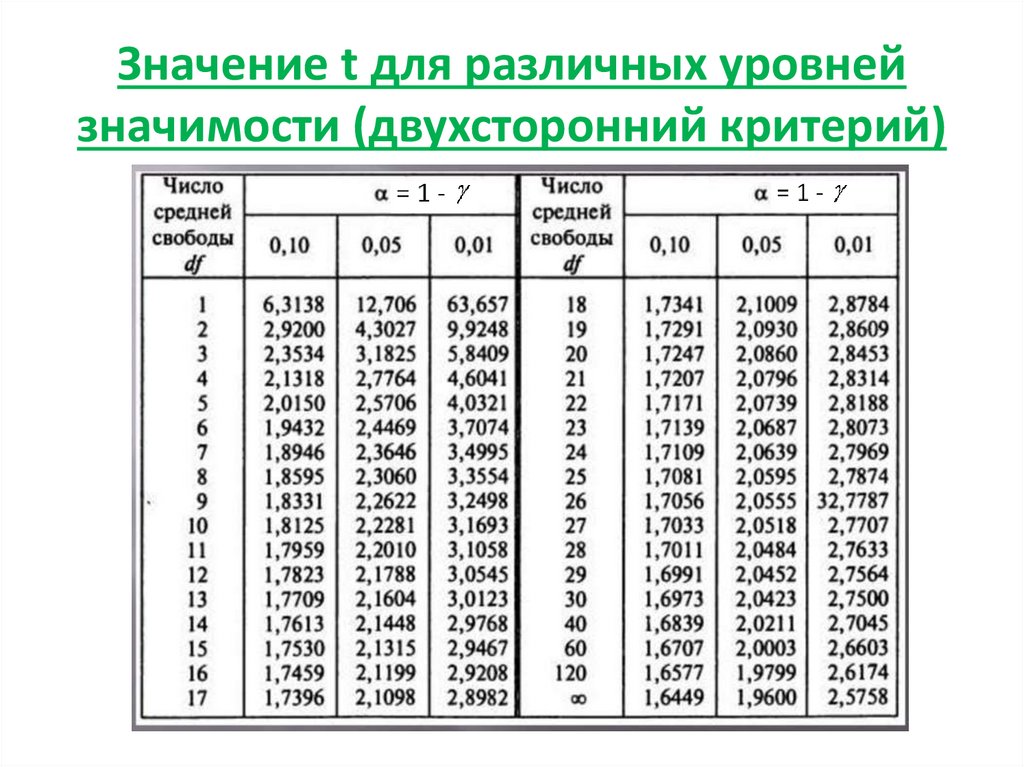
57. Значение t для различных уровней значимости (двухсторонний критерий)
58. Тестирование гипотез
• 2.а). Вычисляем значение тестовой статистики
б). Сравниваем
. Если
то Н0 отвергается в пользу Н1.
,
59. Тестирование гипотез
• 3.а). Вычисляем значение тестовой статистики
б). Сравниваем
. Если
то Н0 отвергается в пользу Н1.
,
60. Проверка значимости коэффициента регрессии
61. Проверка значимости коэффициента регрессии
а). Вычисляем значение тестовой статистики..
б). Сравниваем
. Если
,
то Н0 отвергается в пользу Н1 и говорят, что
коэффициент
значим на заданном
уровне значимости.
62. Проверка значимости коэффициента регрессии
• 1) Незначимые коэффициенты неинтерпретируются, т.е. считается, что
соответствующий ему фактор не влияет на
зависимую переменную у!!!
• 2) значимость
обычно не проверяется.
63. Проверка значимости коэффициента регрессии Пример
64. Проверка значимости коэффициента регрессии Пример
65. Проверка значимости коэффициента регрессии при помощи P-значения
66. Проверка значимости коэффициента регрессии при помощи P-значения
67. Проверка значимости коэффициента регрессии
В R-studio используются обозначения:• -если коэф-т значим на 0,1% уровне ***
• -если коэф-т значим на 1% уровне **
• -если коэф-т значим на 5% уровне *
• -если коэф-т значим на 10% уровне .
68. Доверительный интервал для коэффициента парной регрессии
• Если доверительный интервал включает 0,то коэффициент незначим!!!!!





















































 Математика
Математика








