Похожие презентации:
Производная и дифференциал функции
1. Производная и дифференциал функции
2.
Определение. Пусть функция определена на некоторой окрестноститочки x0 и пусть существует конечный предел отношения
y f ( x0 x) f ( x0 )
x
x
при x 0 Тогда этот предел называется производной функции в точке x0
и обозначается f ( x0 ),
т. е.
f ( x0 ) lim
x 0
f ( x0 x) f ( x0 )
.
x
Операция вычисления производной называется дифференцированием.
Функция, имеющая производную в точке называется дифференцируемой в
этой точке.
Производная функции является также функцией.
3.
Дифференцируемость – более сильное условие на функцию, чемнепрерывность.
Теорема. Всякая функция, дифференцируемая в точке непрерывна в этой
точке.
Доказательство:
y
f ( x0 ) o( x), где o( x) 0 при x 0
x
Следовательно y
т. е. y 0
при
f ( x0 ) x x o( x),
x 0 а следовательно функция
.
непрерывна.
Примечание. Обратное утверждение неверно. Например, функция f ( x) | x |
непрерывна, но не дифференцируема в точке x0 0.
4.
5.
6.
7.
8.
9.
Применение производной в экономикеПусть у(х) — затраты на изготовление х экземпляров некоторого продукта. Тогда у'(х)
выражает скорость изменения затрат при изменении количества продукта. Эта
производная называется предельной (маржинальной) стоимостью.
(Максимизация прибыли). Пусть функция дохода от количества реализованного
товара х выражается формулой R(x) =х3/3 - 2000000 х , а функция затрат на
производство товара формулой С(х) = 1500 х . Определить оптимальный уровень
производства и прибыль, которая при этом достигается.
(Оптимизация налогообложения предприятий ). Пусть функция дохода от
количества реализованного товара х выражается формулой R(x) = 16 х — х2, а
функция затрат на производство товара— формулой С(х) = х2 + 1. Определить
оптимальный уровень налога с единицы реализованного товара и прибыль
предприятия, которая при этом достигается.
Пусть y(t) — величина вклада в момент времени t (в годах). Можно ли определить
(приближенно) годовую ставку банковского процента р по функции y(t)?
Если проценты начисляются непрерывно, то, где р — ежегодный процент прироста
вклада, а r = р/100 — номинальная ставка за год. Найдем логарифмическую
производную от величины вклада: Вывод: ставка банковского процента г совпадет
с логарифмической производной от величины вклада.
Определение эластичности. Понятие эластичности было введено Альфредом
Маршаллом в связи с анализом функции спроса. Впоследствии это понятие было
распространено и на другие функции.
10.
Физический смысл производнойФизический смысл производной. Производная характеризует скорость
изменения одной физической величины по отношению к другой,
считающейся независимой переменной
Механический смысл первой и второй производных. Скорость тела в
момент времени t равна x (t ),
а ускорение равно x (t ), где x(t )
– путь, пройденный телом к моменту времени
Средняя скорость тела за промежуток времени [t0 ; t0 t ]
равна v x .
ср
t
Мгновенная скорость тела в момент времени t 0 есть предел, к которому
стремится его средняя скорость в промежуток времени [t0; t0 t ] при
t 0,
x
x (t0 ).
t 0 t
v(t0 ) lim vср lim
t 0
11.
S1S2
t2
t =t2–t1
S
При Δt 0
t1
S
v
t
мгновенная скорость
S
V
lim
t
t 0
12.
Пусть данная гладкая кривая – график функции y fкасательная
y
f
tg α=
x
f(x0+∆x)
f(x0)
x
B
∆f
A
α
∆x
секущая
∆f
β
α
0
x0
∆x
x
X0 – фиксированное значение аргумента
∆x – приращение аргумента
∆f – приращение функции
x
13.
касательнаяy
B
секущая
A
β
α
0
x0
∆x
∆x→0
∆f→0
x→x0 f(x)→f(x0)
B→A
α→ β
x
x
14.
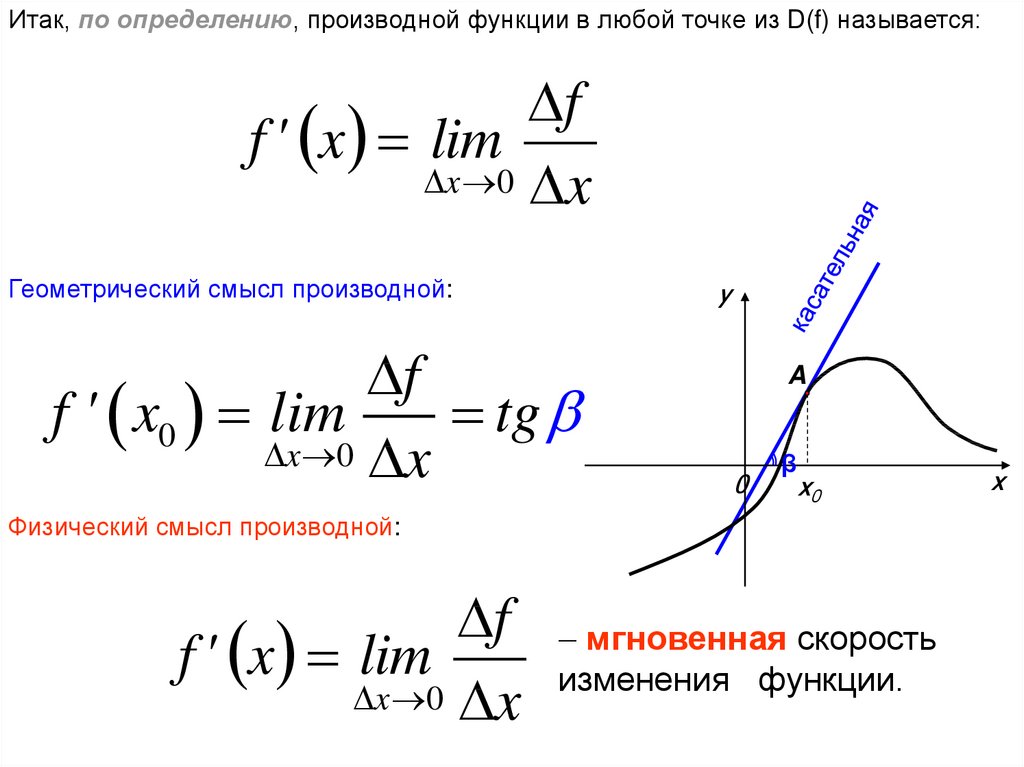
Итак, по определению, производной функции в любой точке из D(f) называется:f
f ' x lim
x 0 x
Геометрический смысл производной:
y
f
f ' x0 lim
tg
x 0 x
A
0
β
x0
Физический смысл производной:
f
f ' x lim
x 0 x
мгновенная скорость
изменения функции.
x
15.
Геометрический смысл производнойГеометрический смысл производной.
Производная функции в точке x0 , равна
тангенсу угла наклона касательной к
графику этой функции, проведенной в точке
с абсциссой
x0
tg f ( x0 ).
Касательная к графику функции y f ( x) в точке x0 , f ( x0 ) – это прямая,
проходящая через точку x0 ; f ( x0 ) и имеющая угловой коэффициент k f ( x0 ).
Уравнение этой прямой называется общим уравнением касательной и
имеет вид
y f ( x0 )( x x0 ) f ( x0 ).
Касательную (в точке ) можно также определить как предельное положение
секущей














 Математика
Математика








