Похожие презентации:
Принятие решений в условиях неопределенности, риска и конфликта
1. Принятие решений в условиях неопределенности, риска и конфликта
2. Классификация типов неопределенностей
неопределенность целей;неопределенность
наших
знаний
об
окружающей обстановке и действующих в
данном
явлении
факторах
(неопределенность природы);
неопределенность действий активного или
пассивного партнера или противника.
2
3. Классификация типов неопределенностей
Можноразличать
стохастическую
(вероятностную)
неопределенность,
когда
неизвестные
факторы
статистически устойчивы и поэтому представляют собой
обычные объекты теории вероятностей - случайные
величины (или случайные функции, события и т.д.).
При этом должны быть известны или определены при
постановке задачи все необходимые статистические
характеристики (законы распределения и их параметры).
Другим крайним случаем может быть неопределенность
нестохастического вида (по выражению Е.С.Вентцель "дурная неопределенность"), при которой никаких
предположений о стохастической устойчивости не
существует.
3
4. Классификация задач принятия решений
1. Принятие решений в условиях определенности,когда данные известны точно.
2. Принятие решений в условиях риска, когда данные
можно
описать
с
помощью
вероятностных
распределений.
3.
Принятие
решений
в
условиях
полной
неопределенности, когда данным нельзя при писать
относительные веса (весовые коэффициенты),
которые представляли бы степень их значимости в
процессе принятия решений.
4. Принятие решений в условиях конфликта
(активного противника).
4
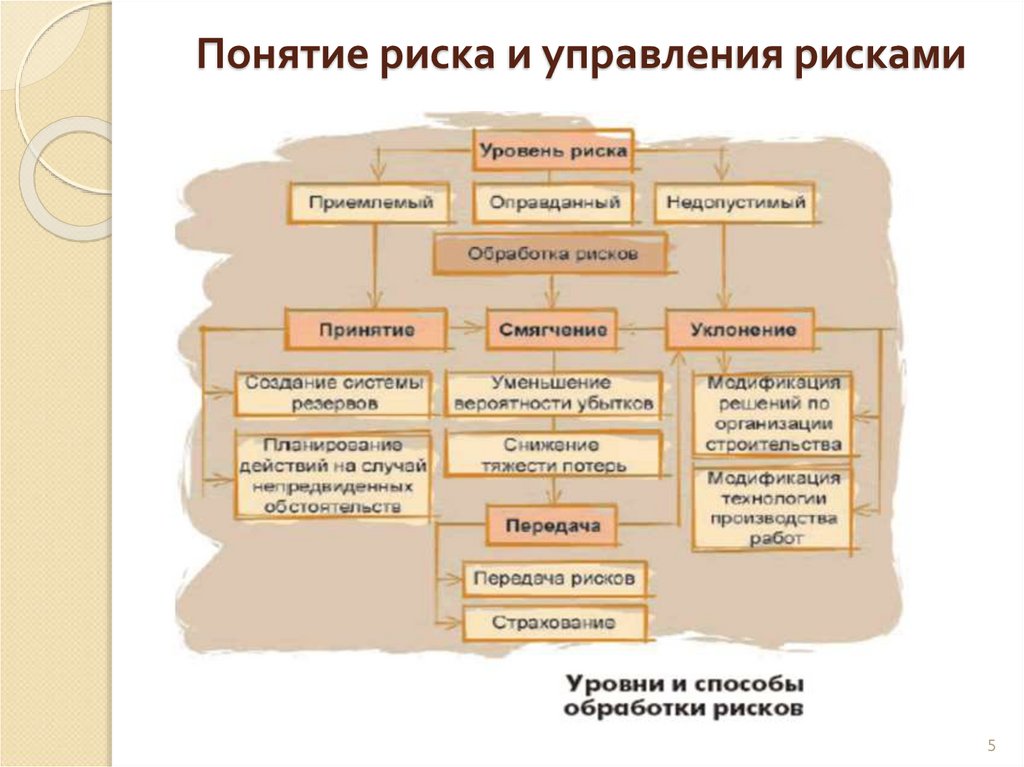
5. Понятие риска и управления рисками
56. Понятие риска и управления рисками
Риск — вероятное событие, которое можетвозникнуть в процессе выполнения работ над
проектом и которое негативно влияет на один или
несколько из ключевых факторов успешного
проектаВероятное
событие,
положительно
влияющее на проект, называется «шансом».
Управление рисками — дисциплина, направленная
на уменьшение влияния рисков на цели и конечное
состояние
проекта.
Управлением
рисками
занимается либо сам руководитель проекта (для
небольших проектов), либо специально выделенный
для этих целей сотрудник (риск-менеджер).
6
7. Понятие риска и управления рисками
Система управления рисками — комплекссредств
автоматизации,
нормативной
и
организационной документации, рабочих процедур,
штатных позиций и конкретных сотрудников их
занимающих, предназначенный для управления
рисками в рамках проектной деятельности
организации.
7
8. Управление рисками
В процессе управления проектными рисками осуществляютсяследующие этапы:
• Идентификация рисков, на котором строится как можно
более полный список рисков, имеющих место в конкретном
проекте. В процессе идентификации конкретизируются
большинство параметров всех выделенных рисков в перечне
их свойств.
• Категоризация рисков, в процессе которой каждому риску
приписывается одна из трёх категорий, влияющая на метод
мониторинга, предотвращения и реагирования на риск.
• Планирование
мониторинга,
предотвращения
и
реагирования на риски, результатом которого будут планы
мониторинга, предотвращения и реагирования на риски
различных категорий. В данных планах должны будут быть
прописаны конкретные ответственные за мониторинг лица,
описан регламент выполнения работ, приведены конкретные
действия по предотвращению или реагированию на риск.
8
9. Управление рисками
• Этап мониторинга, предотвращения и реагирования нариски, который является итеративным и выполняется в
соответствии с плановым регламентом. В рамках данного
процесса на периодической основе происходит возврат к
предыдущим процессам, поскольку для гибкого управления
рисками необходимо постоянно перепланировать в связи с
изменяющимися условиями.
• После окончания проекта (его закрытия) необходимо
провести процедуру анализа эффективности управления
рисками, результатом которой становится аналитическая
записка с выводами относительно успешности управления
рисками, оценками прибыли/расходов в связи с выполнением
процедуры управления рисками, рекомендациями по
изменению базы известных рисков.
• Обновление базы известных рисков, когда в базу вносится
новая информация и новые знания, полученные в процессе
работы над проектом.
9
10. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ РИСКА
• Принимаемое решение основывается на использованиикритерия ожидаемого значения, в соответствии с
которым альтернативные решения сравниваются с
точки зрения максимизации ожидаемой прибыли или
минимизации ожидаемых затрат.
• Использование критерия «ожидаемое значение»
справедливо только в случае, когда одно и тоже
решение приходится применять достаточно большое
число раз. Верно и обратное: ориентация на ожидания
будет приводить к неверным результатам, для решений,
которые приходится принимать небольшое число раз.
• Подход имеет свои недостатки, которые не позволяют
использовать его в некоторых ситуациях, разработаны
модификации упомянутого критерия.
10
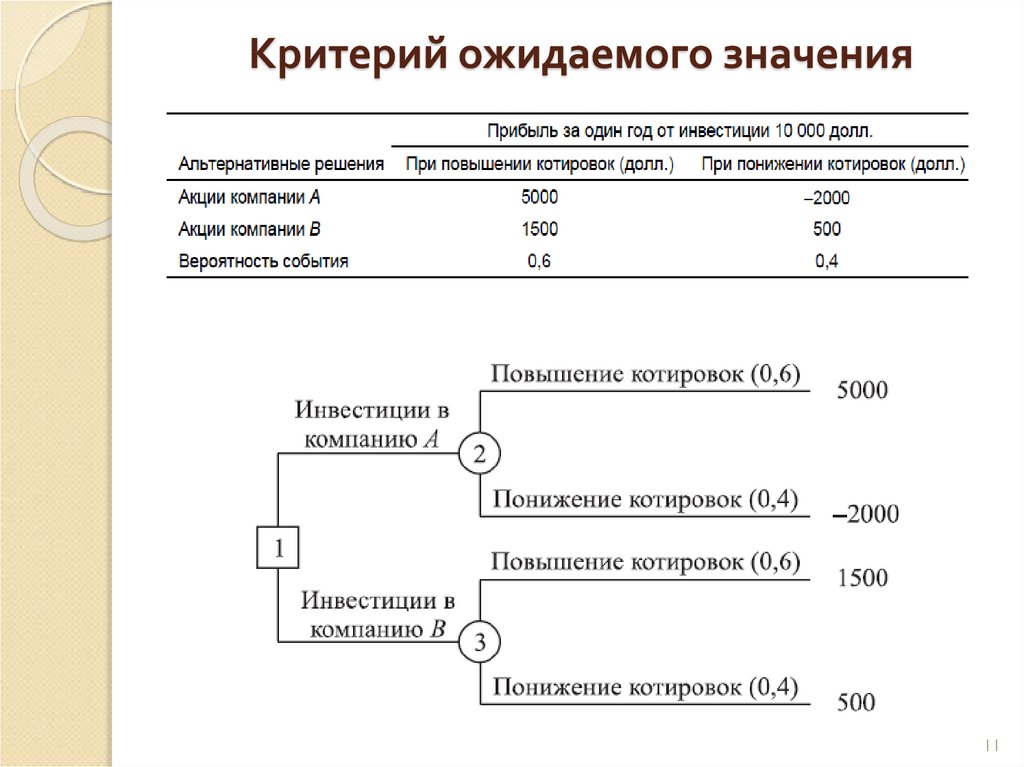
11. Критерий ожидаемого значения
1112. Критерий ожидаемого значения
• Повышение и понижение котировок на биржеименуются состояниями природы, возможные
реализации
которых
являются
случайными
событиями (в данном случае с вероятностями 0,6 и
0,4).
• В общем случае задача принятия решений может
включать n состояний природы и m альтернатив.
• Если pj вероятность j-го состояния природы, а aij
платеж, связанный с принятием решения i при
состоянии природы j (i = 1, 2, ..., m, j = 1, 2, ..., n).
12
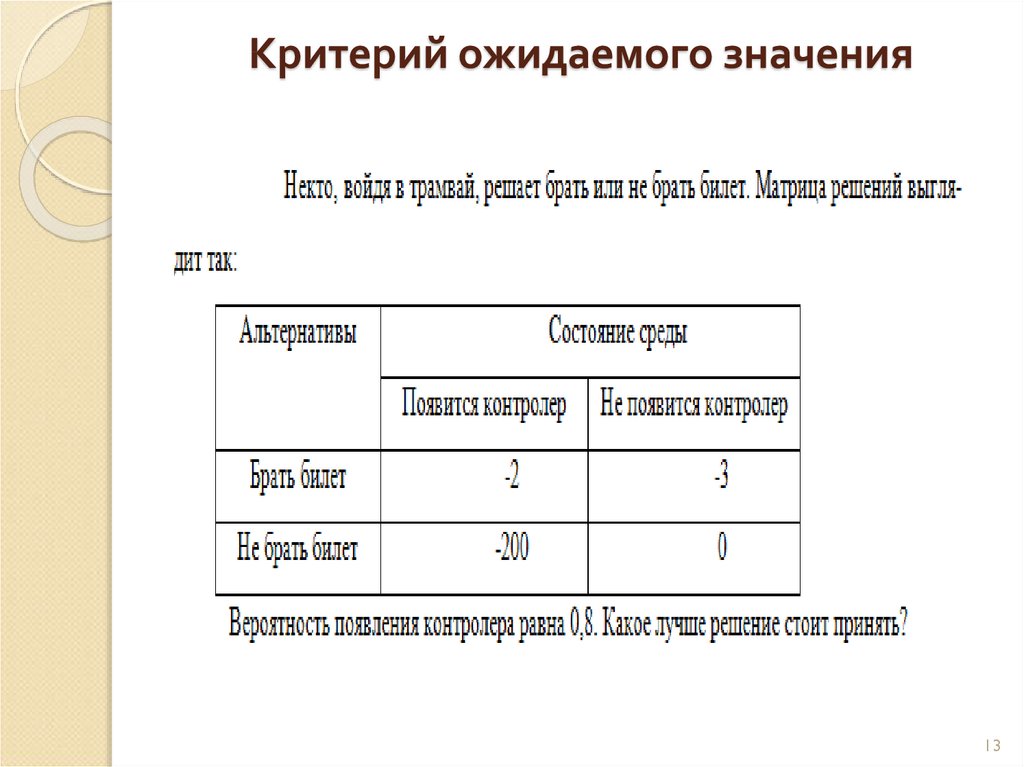
13. Критерий ожидаемого значения
1314. Критерий ожидаемого значения
Ожидаемый платеж для решения i вычисляется ввиде:
МVi = ai1p1 + ai2p2 + ... + ainpn, i = 1, 2, ..., n,
где по определению p1 + p2 + ... + pn = 1.
14
15. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ ПОЛНОЙ НЕОПРЕДЕЛЕННОСТИ
• Принятиерешений
в
условиях
неопределенности, как и в условиях риска,
требует определения альтернативных действий,
которым соответствуют платежи, зависящие от
(случайных) состояний природы.
• Матрица платежей в задаче принятия решений с
m возможными действиями и n состояниями
природы:
15
16. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ ПОЛНОЙ НЕОПРЕДЕЛЕННОСТИ
1. Критерий Лапласа.2. Минимаксный критерий.
3. Критерий Сэвиджа.
4. Критерий Гурвица.
16
17. Критерий Лапласа
Критерий Лапласа опирается на принципнедостаточного основания, который гласит, что,
поскольку распределение вероятностей состояний
Р(sj) неизвестно, нет причин считать их
различными.
Следовательно, используется оптимистическое
предположение, что вероятности всех состояний
природы равны между собой, т.е.
P{s1} = P{s2} = ... = P{sn} = 1/n.
17
18. Максиминный (минимаксный) критерий
Максиминный (минимаксный) критерий основанна консервативном осторожном поведении лица,
принимающего решение, и сводится к выбору
наилучшей альтернативы из наихудших.
Правило выбора решения в соответствии с
максиминным критерием (ММ-критерием) можно
интерпретировать следующим образом:
матрица решений дополняется ещё одним
столбцом из наименьших результатов каждой
строки. Необходимо выбрать те варианты, в
строках которых стоят наибольшее значение
этого столбца :
max min aij
i
j
18
19. Максиминный (минимаксный) критерий
Применение ММ-критерия бывает оправдано,если ситуация, в которой принимается решение
следующая:
1°. О возможности появления внешних состояний
ничего не известно;
2°. Приходится считаться с появлением различных
внешних состояний ;
3°. Решение реализуется только один раз;
4°. Необходимо исключить какой бы то ни было
риск.
19
20. Критерий Сэвиджа
Критерий Сэвиджа стремится смягчить консерватизмминимаксного (максиминного) критерия путем замены
матрицы платежей (выигрышей или проигрышей)
матрицей потерь.
20
21. Критерий Сэвиджа
• Критерий Сэвиджа — тоже крайне пессимистический,но при выборе оптимальной стратегии советует
ориентироваться не на выигрыш, а на риск.
• Данный метод рекомендуется применять, когда
затруднительно построить матрицу решений игры с
природой, но можно тем или иным способом, в крайнем
случае
посредством
экспертного
оценивания,
построить матрицу рисков.
• Выбирается в качестве оптимальной та стратегия, при
которой величина риска в наихудших условиях
минимальна.
21
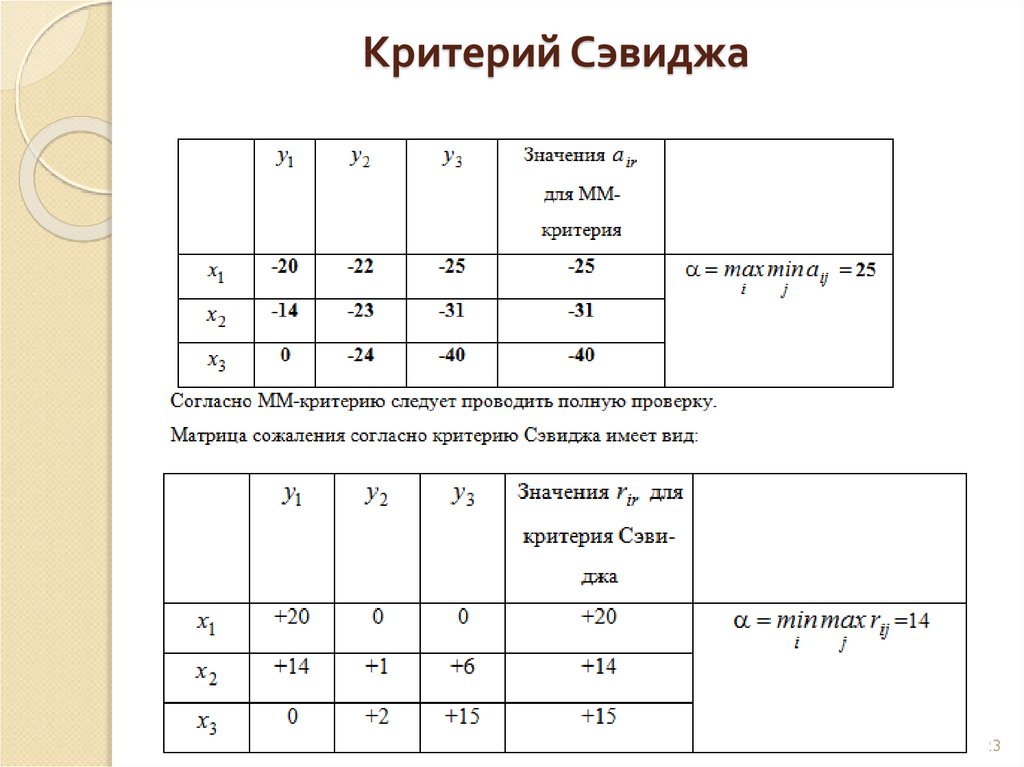
22. Критерий Сэвиджа
Пример:При
работе
ЭВМ
необходимо
периодически
приостанавливать обработку информации и проверять
ЭВМ на наличие в ней вирусов. Приостановка в
обработке информации приводит к определённым
экономическим издержкам.
В случае же если вирус вовремя обнаружен не будет,
возможна потеря и некоторой части информации, что
приведёт и ещё к большим убыткам. Варианты решения
таковы:1 - полная проверка; 2- минимальная проверка; -3
отказ от проверки. ЭВМ может находиться в следующих
состояниях: 1- вирус отсутствует; 2- вирус есть, но он не
успел повредить информацию;3 - есть файлы,
нуждающиеся в восстановлении. Найти решение
проблемы с помощью ММ-критерия и критерия
Сэвиджа.
22
23. Критерий Сэвиджа
2324. Критерий Сэвиджа
• Ясно, что вследствие их жёстких исходныхпозиций
они
применимы
только
для
идеализированных практических решений.
• В случае, когда возможна слишком сильная
идеализация, можно применять одновременно
поочерёдно различные критерии.
• После этого среди нескольких вариантов ЛПР
волевым методом выбирает окончательное
решение.
• Такой подход позволяет, во-первых, лучше
проникнуть во все внутренние связи проблемы
принятия решений и, во-вторых, ослабляет
влияние субъективного фактора.
24
25. Критерий пессимизма-оптимизма Гурвица
• Стараясь занять наиболее уравновешеннуюпозицию, Гурвиц предположил оценочную
функцию, которая находится где-то между
точкой зрения крайнего оптимизма и
крайнего пессимизма:
max{ min aij (1 ) max aij }
i
где
j
j
- коэффициент пессимизма .
25
26. Критерий пессимизма-оптимизма Гурвица
• Если = 0, критерий Гурвица становитсяконсервативным,
так
как
его
применение
эквивалентно применению обычного минимаксного
критерия.
• Если = 1, критерий Гурвица становится слишком
оптимистичным, ибо рассчитывает на наилучшие из
наилучших условий.
• Мы можем конкретизировать степень оптимизма
(или пессимизма) надлежащим выбором величины
из интервала [0, 1]. При отсутствии ярко
выраженной
склонности
к
оптимизму
или
пессимизму выбор = 0,5 представляется
наиболее разумным.
26
27. Критерий пессимизма-оптимизма Гурвица
Критерий Гурвица применяется в случае, когда :1°. о вероятностях появления состояния ничего не
известно;
2°. с появлением состояния необходимо считаться;
3°. реализуется только малое количество решений;
4°. допускается некоторый риск.
27
28. Теория игр
В теории игр рассматриваются ситуации, связанные спринятием решений, в которых два разумных
противника имеют конфликтующие цели.
К
числу
типичных
примеров
относится
рекламирование
конкурирующих
товаров
и
планирование
военных
стратегий
противоборствующих армий.
Эти ситуации принятия решений отличаются от
рассмотренных ранее, где природа не рассматривается
в роли недоброжелателя.
28
29. Теория игр
Первыми провели исследование в области теории игр Дж-ФНейман и О.Моргенштерн и описали результаты в книге
"Теория игр и экономическое поведение" (1944) .
Игра
идеализированная
математическая
модель
коллективного поведения: несколько игроков влияют на
исход игры, причем их интересы различны.
Вначале были изучены игры с чистым конфликтом (игры с
нулевой суммой).
Принципы «чистого антагонизма» не могли работать в
большинстве игр, разыгрываемых в реальной жизни,
поскольку взаимосвязь действий людей определялась не
только конфликтом, но и сотрудничеством.
В дальнейшем Томас Шеллинг расширил анализ игр с
последовательными ходами, разработав идеи стратегических
ходов.
29
30. Теория игр
Развитие игры во времени можно представлять какряд последовательных «ходов» участников.
Ходом называется выбор игроком одного из
предусмотренных правилами игры действий и его
осуществление.
Ходы бывают личные и случайные. При личном ходе
игрок сознательно выбирает и осуществляет тот или
другой вариант действий (пример — любой ход в
шахматах).
При случайном ходе выбор осуществляется не волей
игрока, а каким-то механизмом случайного выбора
(бросание монеты, игральной кости, вынимание
карты из колоды и т. п.).
30
31. Теория игр
Некоторые игры (так называемые «чисто азартные»)состоят только из случайных ходов — ими теория игр
не занимается.
Ее цель — оптимизация поведения игрока в игре, где
(может быть, наряду со случайными) есть личные
ходы. Такие игры называются стратегическими.
Стратегией игрока называется совокупность правил,
определяющих выбор варианта действий при каждом
личном ходе в зависимости от сложившейся
ситуации.
Обычно, участвуя в игре, игрок не следует какимлибо жестким, «железным» правилам: выбор
(решение) принимается им в ходе игры, когда он
непосредственно наблюдает ситуацию.
31
32. Теория игр
Однако теоретически дело не изменится, еслипредположить, что все эти решения приняты игроком
заранее («если сложится такая-то ситуация, я поступлю
так-то»).
Это будет значить, что игрок выбрал определенную
стратегию. Теперь он может и не участвовать в игре
лично, а передать список правил незаинтересованному
лицу (судье).
Стратегия также может быть задана машине-автомату в
виде программы (именно так играют в шахматы ЭВМ).
32
33. Теория игр
Оптимальной стратегией игрока называется такая,которая обеспечивает ему наилучшее положение в
данной игре, т. е. максимальный выигрыш.
Если игра повторяется неоднократно и содержит,
кроме личных, еще и случайные ходы, оптимальная
стратегия обеспечивает максимальный средний
выигрыш.
Основное предположение, исходя из которого
находятся оптимальные стратегии, состоит в том, что
противник (в общем случае — противники) по меньшей
мере так же разумен, как и сам игрок, и делает все для
того, чтобы добиться своей цели. Расчет на разумного
противника — лишь одна из возможных позиций в
конфликте, но в теории игр именно она кладется в
основу.
33
34. Теория игр
В игровом конфликте участвуют противники,именуемые игроками, каждый из которых имеет
некоторое множество (конечное или бесконечное)
возможных выборов, которые называются стратегиями.
С каждой парой стратегий связан платеж, который один
из игроков выплачивает другому. При обозначении
игроков через А и В с числом стратегий m и n
соответственно игру обычно представляют в виде
матрицы платежей игроку А:
a11 a12
a21 a22
A
...
...
am1 am 2
... a1n
... a2 n
... ...
... amn
34
35. Классификация игр
Игры можнопризнакам.
классифицировать
по
различным
1.
По количеству игроков (игры 2 и n игроков). Игра,
в которой участвуют два игрока, называется парной.
2.
По количеству стратегий. В зависимости от
числа стратегий игры делятся на «конечные» и
«бесконечные». Игра называется конечной, если у
каждого игрока имеется в распоряжении только
конечное число стратегий (в противном случае игра
называется бесконечной). Бывают игры (например,
шахматы), где в принципе число стратегий конечно, но
так велико, что полный их перебор практически
невозможен.
35
36. Классификация игр
3. По характеру взаимодействия игроков.По характеру взаимодействия игроков игры делятся
на:
бескоалиционные – игроки не имеют права вступать в
соглашения, образовывать коалиции;
коалиционные
(кооперативные)– игроки могут
вступать в коалиции.
4.
По характеру выигрыша.
По характеру выигрыша игры можно разделить на
антагонистические и игры с ненулевой суммой.
Игра называется игрой с нулевой суммой , если сумма
выигрышей всех игроков в любой игровой ситуации
равна нулю (т. е. каждый игрок выигрывает только за
36
счет других).
37. Классификация игр
5.По характеру получения информации.
По характеру получения информации игры
делятся на:
игры в нормальной форме – игроки получают всю
предназначенную им информацию до начала
игры;
динамические игры – информация поступает
игрокам в процессе развития игры.
37
38. Матричные игры
Парная, конечная, антагонистическая игра называетсяматричной.
Рассмотрим такую игру G(X,Y,K), в которой участвуют два
игрока, имеющие противоположные интересы: выигрыш
одного равен проигрышу другого, первый игрок хочет
максимизировать, а второй — минимизировать.
X и Y -- непустые множества стратегий для 1 и 2 игроков
соответственно, элементы декартова произведения X×Y
(т.е. пары стратегий (x,y), где x , y --ситуации), а функция К:
X×Y→R называется функцией выигрыша первого игрока.
a11 a12
a21 a22
A
...
...
am1 am 2
... a1n
... a2 n
... ...
... amn
38
39. Матричные игры
Главным в исследовании игроптимальных стратегий игроков.
Стратегия игрока является оптимальной, если
применение этой стратегии обеспечивает ему
наибольший
гарантированный
выигрыш
при
всевозможных стратегиях другого игрока.
Исходя из этих позиций, игрок 1 исследует матрицу
выигрышей А следующим образом: для каждого
значения i (i =1,2,...,m) определяется минимальное
значение выигрыша в зависимости от применяемых 2-м
игроком стратегий j ( i =1,2,...n):
является
понятие
min aij (i 1,m )
j
39
40. Матричные игры
.Т.е. определяется минимальный выигрыш для игрока 1
при условии, что он примет свою i-ю чистую
стратегию, а затем из этих минимальных выигрышей
отыскивается такая стратегия i = io, при которой
этот минимальный выигрыш будет максимальным,
т.е. находится: max min aij v
i
j
i 1,m,
j 1,n
Принцип оптимальности в поведении 1-го игрока,
который заключается в достижении им наибольшего
гарантированного выигрыша, называется принципом
максимина
40
41. Матричные игры
.Игрок 2 при оптимальном своём поведении должен
стремиться по возможности за счёт своих стратегий
максимально уменьшить выигрыш игрока 1
Для игрока 2 отыскивается , т.е. определяется
максимальный проигрыш игрока 1, при условии, что
игрок 2 применит свою j-ю стратегию. При этом
наименьший из возможных проигрышей составит
v min max aij
i 1,m,
j 1,n
j
i
Число называется верхней иеной игры. Принцип
оптимальности в поведении 2-го игрока, который
заключается в достижении им наименьшего из
возможного
проигрыша,
называется
принципом
минимакса, т.е. это минимакс. Оптимальная
стратегия 2-го игрока, при которой достигается ,
называется минимаксной.
41
42. Матричные игры
.Игры, в которых достигается ситуация равновесия, называются
вполне определенными.
42
43. Матричные игры
.• Исследование в матричных играх начинается с
нахождения её седловой точки в чистых
стратегиях.
• Если матричная игра имеет седловую точку в
чистых стратегиях, то нахождением этой седловой
точки заканчивается исследование игры.
• Если же в игре нет седловой точки в чистых
стратегиях, то можно найти нижнюю и верхнюю
чистые цены этой игры, которые указывают, что
игрок 1 не должен надеяться на выигрыш больший,
чем верхняя цена игры, и может быть уверен в
получении выигрыша не меньше нижней цены
игры.
43
44. Матричные игры
.• Улучшение решений матричных игр следует
искать
в
использовании
секретности
применения чистых стратегий и возможности
многократного повторения игр в виде партии.
• Этот результат достигается путём применения
чистых стратегий случайно, с определённой
вероятностью.
44
45. Матричные игры
.Смешанной стратегией игрока называется полный
набор вероятностей применения его чистых стратегий.
45
46. Матричные игры
.• Чистая стратегия есть частный случай смешанной
стратегии. Действительно, если в смешанной
стратегии
какая-либо
i-я
чистая
стратегия
применяется с вероятностью 1, то все остальные
чистые стратегии не применяются. И эта i-я чистая
стратегия является частным случаем смешанной
стратегии.
• Оптимальная стратегия игрока – это стратегия,
обеспечивающая ему максимально возможный
гарантированный средний выигрыш при достаточно
большом повторении ходов игры.
• Средний выигрыш игрока K(X,Y) 1 в матричной игре
с матрицей А выражается в виде математического
ожидания его выигрышей:
m n
K(X,Y) M ( A, x, y ) aij pi q j xAy T
i 1 j 1
46
47. Матричные игры
.• (х*, у*) называются оптимальными смешанными
стратегиями соответственно игроков 1 и 2, если
они образуют седловую точку:
M(А, х, y*) M(А, х*, y*) M(А, х*, у)
Оптимальные смешанные стратегии и цена игры
(х* ,у*, v) называются решением матричной игры.
Теорема:
Всякая матричная игра имеет ситуацию равновесия
(седловую точку) в смешанных стратегиях.
47
48. Свойства решений матричных игр
Обозначим через G (X, Y,K) игру двух лиц с нулевойсуммой, в которой игрок 1 выбирает стратегию х X,
игрок 2 - у У, после чего игрок 1 получает выигрыш
K(х, у) за счёт игрока 2.
Стратегия
x1 игрока 1 доминирует (строго
доминирует) над стратегией x2, если К(x1,у)≥K(x2,у)
(К(x,у)>K(x,у)) для всех у Y.
Стратегия y1 игрока 2 доминирует y2 (строго
доминирует) над стратегией , если K(х,y1)≤K(х,y2)
(K(х,y1)<K(х,y2)) для всех х Х.
При
этом стратегии x2 и y2 называются
доминируемыми (строго доминируемыми).
48
49. Свойства решений матричных игр
Спектром смешанной стратегии игрока в конечной антагонистической игреназывается множество всех его чистых стратегий, вероятность которых
согласно этой стратегии положительна.
49
50. Свойства решений матричных игр
5051. Свойства решений матричных игр
Замечание. Отметим, что исключение доминируемых (нестрого) стратегий может привести к потере некоторых решений.
Если же исключаются только строго доминируемые стратегии, то
множество решений игры не изменится.
51
52. Свойства решений матричных игр
3. Тройка (х*, y*,v) являетсярешением игры G = (Х,Y,A) тогда
и только тогда, когда
(х*, y*, av +b) является решением
игры G (Х,Y,aA+B), где B —
матрица, в которой все элементы
равны b, a > 0.
52
53. Сведение матричной игры к задаче линейного программирования
Связь между теорией игр и линейнымпрограммированием была установлена в
1951 году американским математиком
Данцигом с помощью теоремы.
Доказательство
указанной
теоремы
заключается в сведении матричной игры к
паре двойственных задач линейного
программирования.
53
54. Сведение матричной игры к задаче линейного программирования
Разделим все уравнения и неравенства в (1) и (2) на v (это можносделать, т.к. по предположению v > 0) и введём обозначения :
54
55. Сведение матричной игры к задаче линейного программирования
5556. Сведение матричной игры к задаче линейного программирования
5657. Сведение матричной игры к задаче линейного программирования
5758. Сведение матричной игры к задаче линейного программирования
x* ( vx1 ,...,vx m )(i = 1, m )
y* ( vy1 ,...,vy m )
(j = 1, n )
V=1/F
58
59. Сведение матричной игры к задаче линейного программирования
1 2 0A1 1 0 1
2 1 0
59
60. Матричные игры
6061. Матричные игры
6162. Матричные игры
V=15/7-3=-6/762
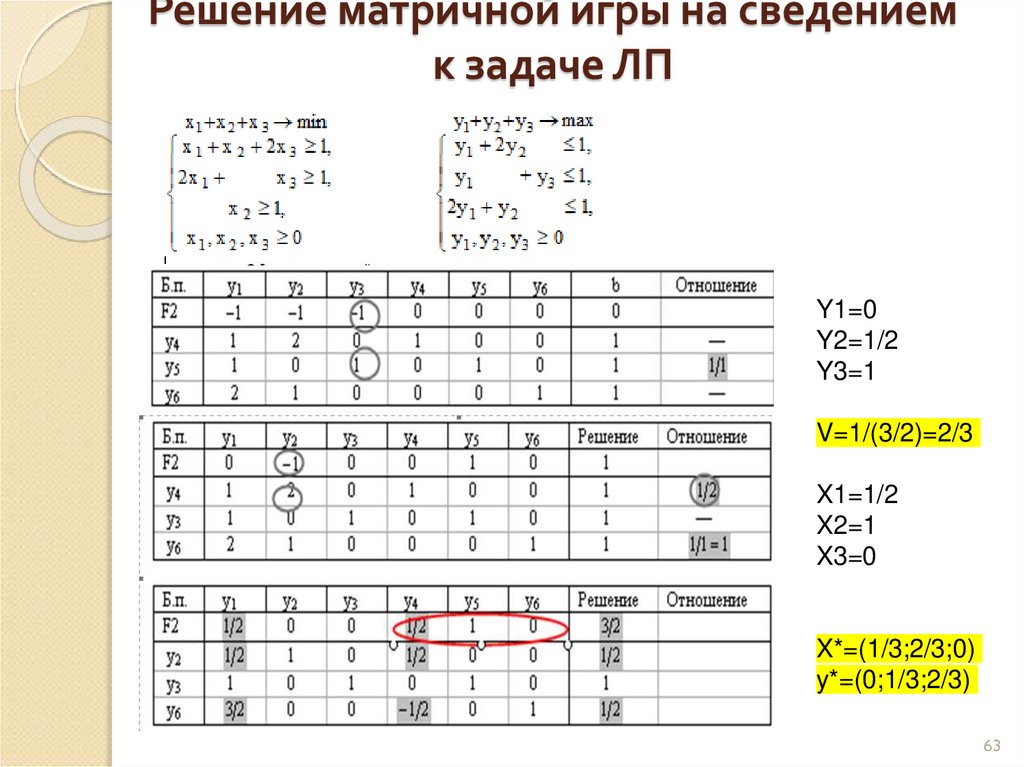
63. Решение матричной игры на сведением к задаче ЛП
Y1=0Y2=1/2
Y3=1
V=1/(3/2)=2/3
X1=1/2
X2=1
X3=0
X*=(1/3;2/3;0)
y*=(0;1/3;2/3)
63
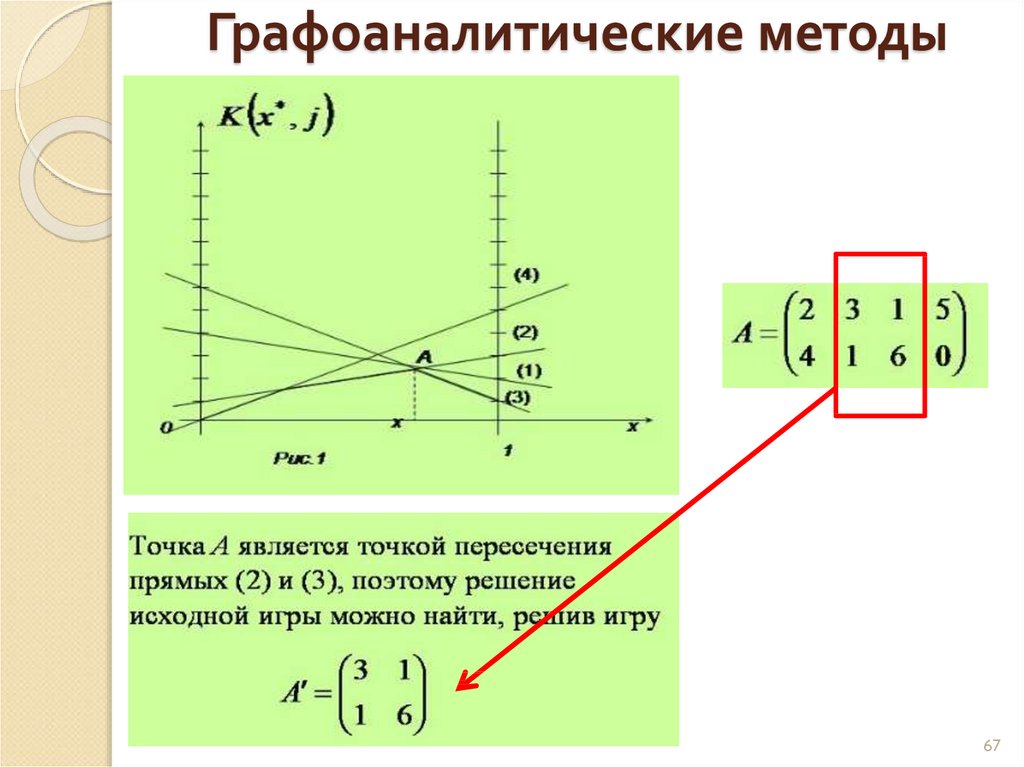
64. Матричные игры. Графоаналитические методы
6465. Графоаналитические методы
6566. Графоаналитические методы
6667. Графоаналитические методы
6768. Графоаналитические методы
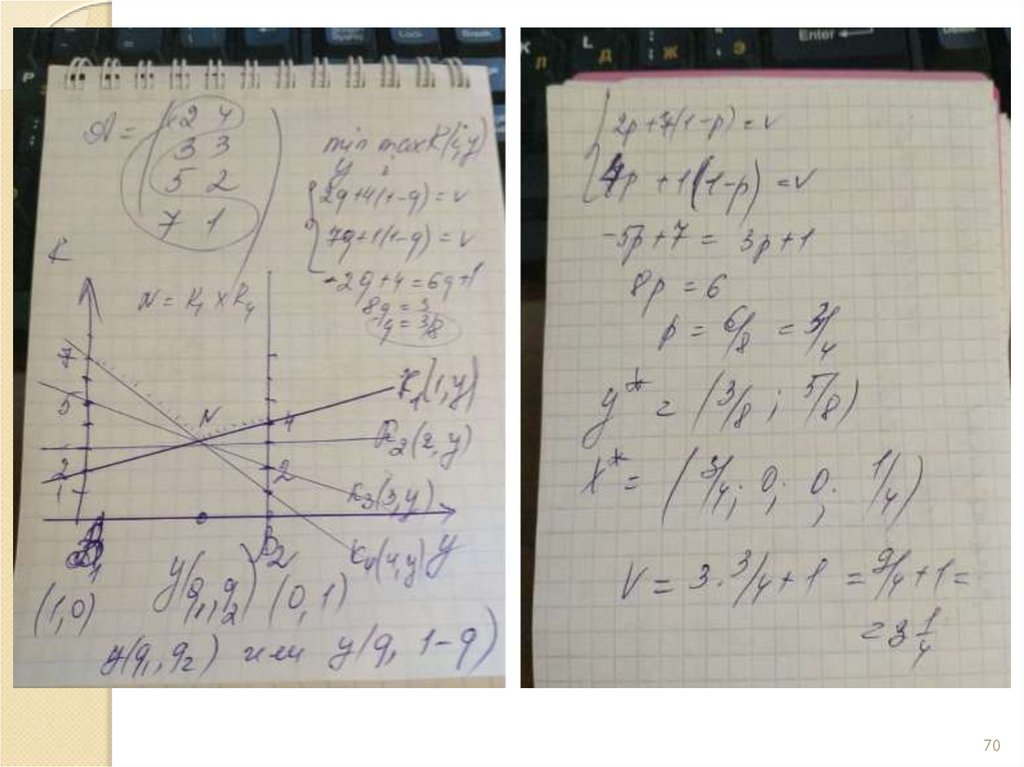
6869. Графоаналитические методы
6970.
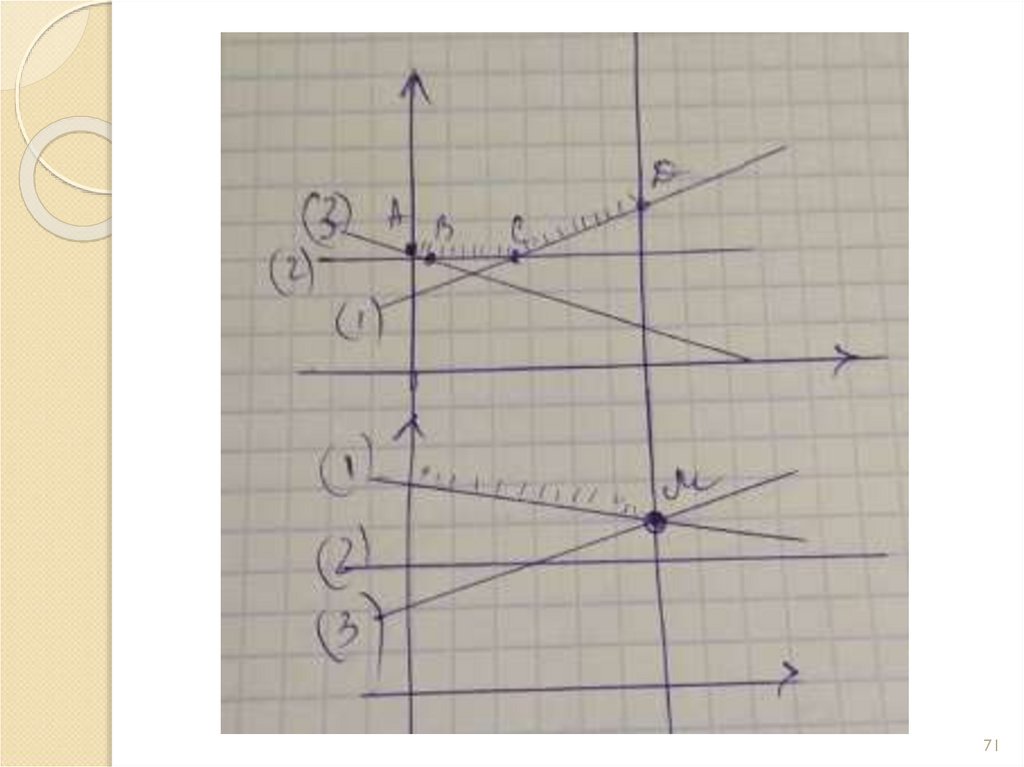
7071.
7172.
7273. Матричные игры. Метод Брауна-Робинсона
Матричные игры. Метод БраунаРобинсона73
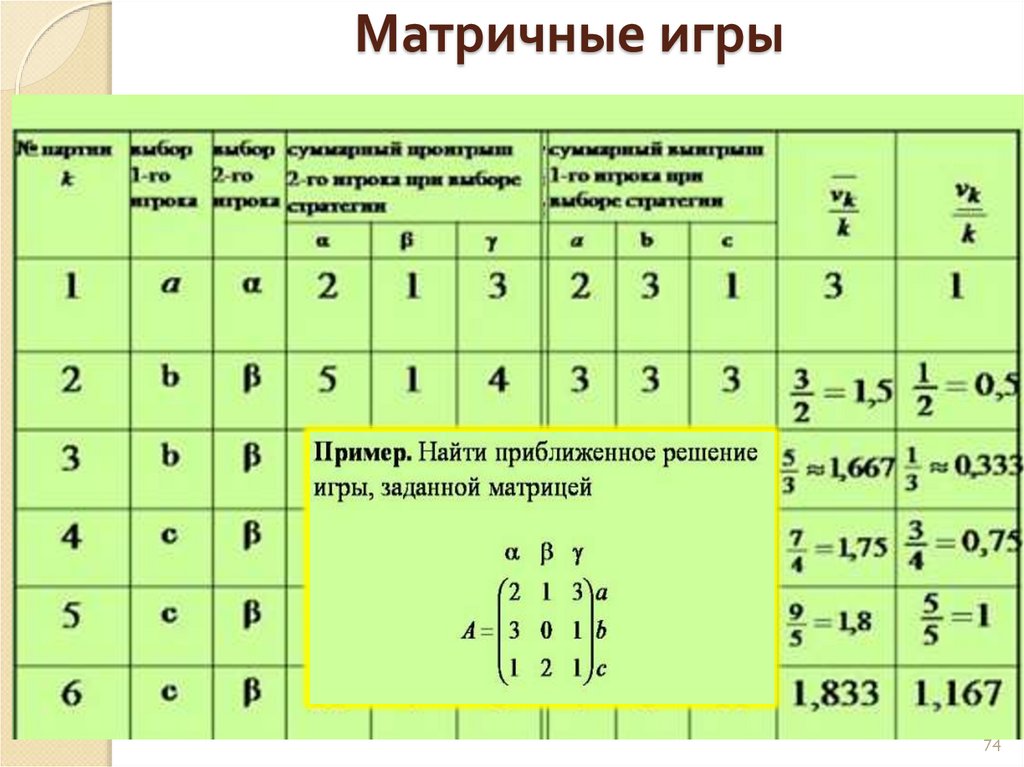
74. Матричные игры
7475. Матричные игры
7576. ИГРЫ С НУЛЕВОЙ И ПОЛОЖИТЕЛЬНОЙ СУММОЙ
Игра с нулевой суммой, предусматривающий такойвыигрыш, состоящий исключительно из проигрыша
других игроков, польза одних непременно должна
образовываться за счет потерь других игроков, сумма
пользы и потерь всегда равна нулю.
Вторая категория - игра с положительной суммой, когда
индивидуальные игроки соревнуются за выигрыш,
состоящий из их же ставок.
В обоих случаях игра неизбежно сопряжена с риском,
поскольку каждый из ее участников, как считали
исследователи,
стремится
максимально
повысить
функцию, переменные которой им не контролируются.
76
77. КООПЕРАТИВНЫЕ ИГРЫ
Кооперативной игрой называется игра с ненулевойсуммой, в которой игрокам разрешается обсуждать
перед игрой свои стратегии и договариваться о
совместных действиях, т.е. игроки могут образовывать
коалиции.
Основная задача в кооперативной игре состоит в
делении общего выигрыша между членами коалиции.
В случае игры двух лиц предполагается, что два игрока
не могут воздействовать друг на друга, пока не придут к
некоторому соглашению.
77
78. ИГРЫ С НУЛЕВОЙ И ПОЛОЖИТЕЛЬНОЙ СУММОЙ
Если все игроки одинаково умелые, торешающим фактором становится случайность.
Но так бывает редко.
Почти всегда важную роль в игре играет
хитрость, с помощью которой делаются попытки
раскрыть замыслы противников и завуалировать
свои намерения, а затем занять выгодные
позиции,
которые
заставили
бы
этих
противников действовать в ущерб самим себе.
78
79. Джон Форбс Нэш
Очень сильная личность и Нобелевскийлауреат Джон Нэш является ученым,
который много и плодотворно работал в
сфере дифференциальной геометрии и
теории игр.
Математик многие годы своей жизни
посвятил
трагической
борьбе
с
собственным безумием, граничащим с
гениальностью.
«Хорошие научные идеи не приходили
бы мне в голову, если бы я думал как
нормальные люди.»
Д. Нэш
79
80. Биматричные игры
Биматричная игра – модель конфликта, вкотором интересы игроков различны, но не
обязательно противоположны: каждый – сам за
себя.
Хотя
в некоторых играх этого класса
предполагается
возможность
определенного
информационного обмена или поступления
дополнительной информации, вообще говоря,
возможность кооперации игроков и образования
их коалиций не рассматривается, т.е. считается,
что
игроки
принимают
решения,
не
договариваясь друг с другом.
Анализ таких игр оказывается полезным, в том
числе для определения возможных вариантов
сотрудничества и «просчета» их результатов.
80
81. Биматричные игры
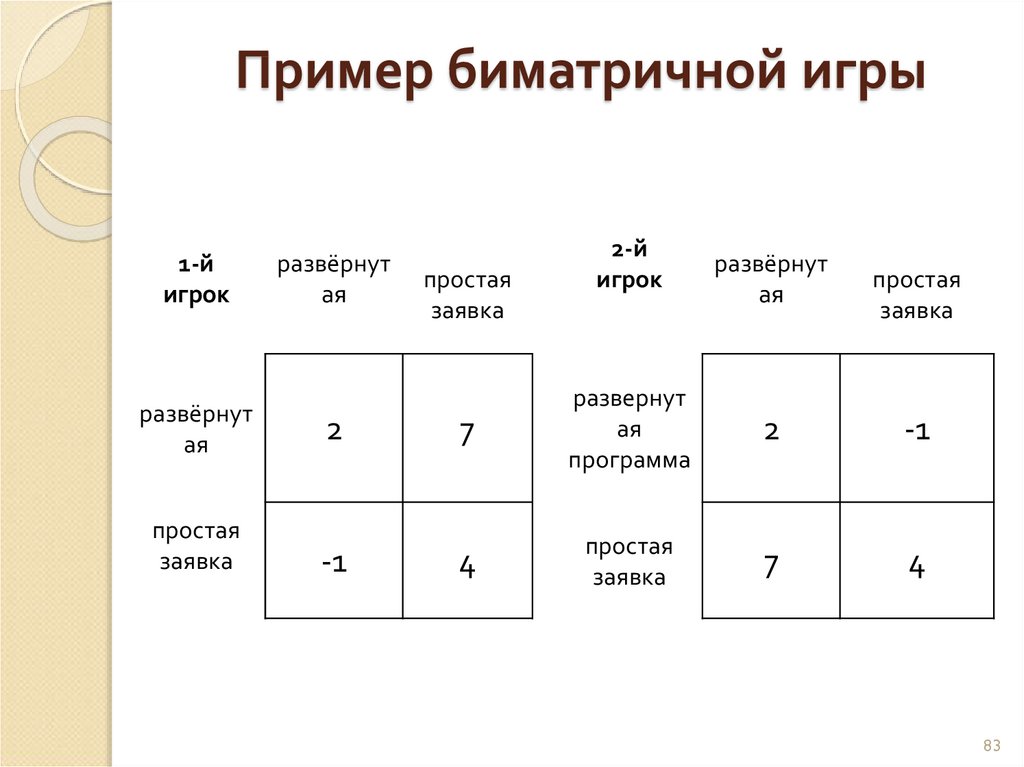
8182. Пример биматричной игры
Конкурс на реализацию проектаДве фирмы, борющиеся за заказ на определенную
работу, могут выбрать два варианта - подать
развернутую программу (1-я стратегия) или простую
заявку (2-я стратегия).
Согласно правилам при одинаковом выборе
конкурентов заказ и доход делятся пополам, а в
другом случае предпочтение отдается фирме,
подавшей подробную заявку.
На реализацию проекта победителям (одному или
двоим)
выделяется
10
тысяч
долларов.
Технические затраты на простую заявку - 1 тысяча
долларов, на развернутую программу - 3 тысячи
долларов.
82
83. Пример биматричной игры
01-йигрок
развёрнут
ая
развёрнут
ая
2
простая
заявка
-1
простая
заявка
2-й
игрок
развёрнут
ая
простая
заявка
7
развернут
ая
программа
2
-1
4
простая
заявка
7
4
83
84. Пример биматричной игры. Дилемма заключенного
"Игроками" являются двое заключенных, обвиняемых всовершении тяжелого преступления, их стратегиями сознаваться или не сознаваться.
Если оба сознаются (в матрице это 1-я строка и 1-й
столбец), то получат большой срок заключения, но не
максимальный.
Если оба не сознаются (2-я строка и 2-й столбец), то их
осудят за менее тяжкие преступления, в которых они уже
уличены.
Если сознается только один, то его срок заключения будет
значительно снижен, а другой получит максимальный срок.
(Числа в матрицах - это сроки заключения, взятые с
противоположным знаком.)
84
85. Биматричные игры
Процесс нахождения ситуаций равновесияв биматричной игре часто называется
решением игры.
Джорджем
Нэшем
было
доказано
существование ситуации равновесия в
смешанных стратегиях для любой
биматричной игры.
Поведение игроков в биматричных играх
направлено не на повышение своего
выигрыша, а на желание держать под
контролем выигрыш другого игрока
(минимизировать этот выигрыш) – задачи
на нарушение квот на добычу нефти,
политические
решения,
военное
вооружение и т.д.
85
86. Биматричные игры
8687. Три недостатка понятия равновесия по Нэшу
равновесий Нэша в игре можетне существовать;
равновесие Нэша может быть
не единственно;
равновесие Нэша может быть
неэффективно.
87
88. Биматричные игры
В теории игр равновесием Нэша (названным в честь ДжонаФорбса Нэша, который предложил его) называется тип
решений игры двух и более игроков, в котором ни один
участник не может увеличить выигрыш, изменив своё
решение в одностороннем порядке, когда другие
участники не меняют решения. Такая совокупность
стратегий выбранных участниками и их выигрыши
называются равновесием Нэша.
Из определения видно, что в ситуациях равновесия и только
в них ни один игрок не заинтересован в отклонении от своей
стратегии.
В частности, если ситуация равновесия оказывается
предметом договора между игроками, то ни один из игроков
не будет заинтересован в нарушении своих обязательств.
88
89.
8990. Биматричные игры
Нахождение ситуации равновесия вчистых стратегиях.
В каждом столбце матрицы A пометьте
звездочкой максимальные элементы.
Затем
пометьте
звездочкой
максимальные элементы в каждой
строке матрицы B.
Запишите все пары стратегий (i, j),
такие, что оба элемента aij и bij
отмечены звездочкой.
Все эти пары являются ситуациями
равновесия.
90
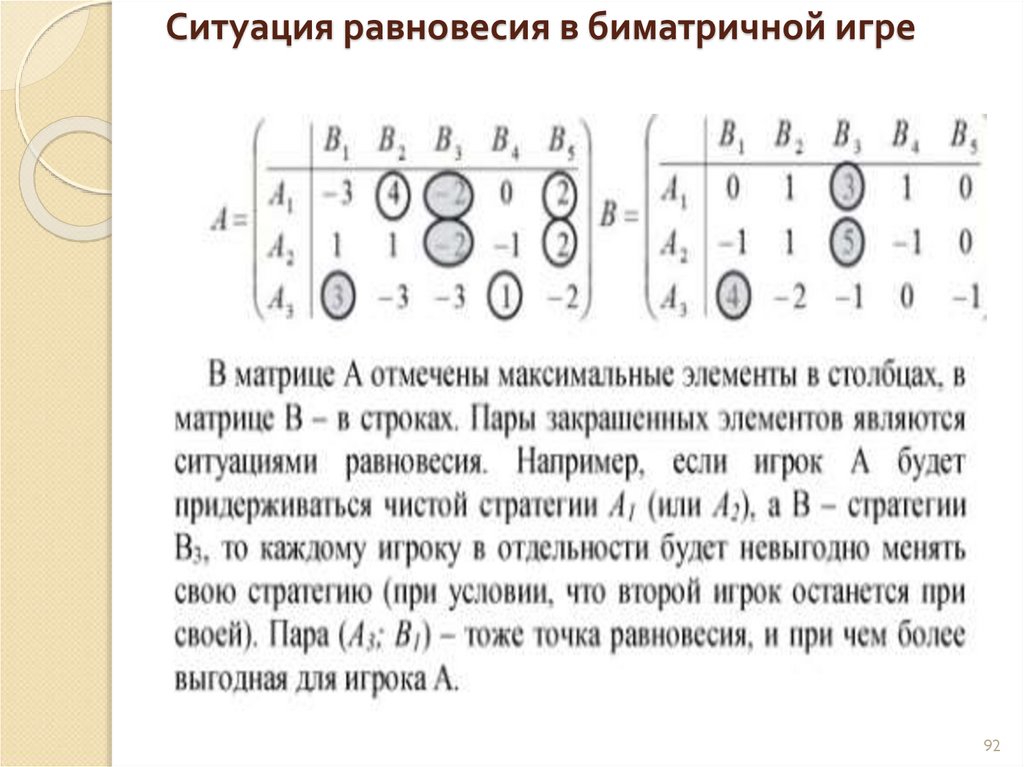
91. Ситуация равновесия в биматричной игре
Ситуация равновесия в биматричной игре такжеопределяется по Нэшу:
aij* ai* j*
bi* j bi* j*
Решить биматричную игру – найти все ситуации
равновесия и указать выигрыши каждого игрока в
них.
91
92. Ситуация равновесия в биматричной игре
9293. Ситуация равновесия в биматричной игре
9394. Биматричные игры
Существенным отличием биматричных игр отматричных являются то, что возможны
ситуации, когда отклонение обоих игроков
от максиминных стратегий приводит к
увеличению их выигрышей.
В моделях биматричных игр присутствует
противоречие
между
выгодностью
и
устойчивостью: устойчивые решения не
всегда являются выгодными для игроков.
94
95.
9596. Проблема эффективности равновесия Нэша
В этой игре существует единственная точка равновесияНэша обоим сознаться.
Но есть ситуация, которая выгоднее обоим игрокам это
обоим не сознаваться. Следовательно, точки равновесия
Нэша могут быть неэффективны в том смысле, что за счет
отклонения обоих игроков от точки равновесия Нэша
можно улучшить выигрыши каждого из них.
Чтобы
сформулировать
обнаруженное
свойство
неэффективности равновесий Нэша более формально,
введем понятие Парето-оптимальной ситуации.
96
97. Биматричные игры
9798. Биматричные игры
Формальное различие между ситуацией равновесия иситуацией, оптимальной по Парето: в первой ни один
игрок, действуя в одиночку, не может увеличить
своего собственного выигрыша, а во второй оба
игрока, действуя совместно, не могут (даже нестрого)
увеличить выигрыш каждого.
Выбор Парето-оптимальной пары стратегий может
приводить к ситуациям, более выгодным для обоих
участников, чем ситуации равновесия.
Для матричных игр ситуация равновесия и Паретооптимальность – равносильные понятия.
98
99. Решения биматричной игры.
• Точка равновесия - (А2,В2). В то же время исход (А1,В1) ситуация(А1, В1) является оптимальной по Парето, дает больший выигрыш
для обоих игроков. Т.о., некооперативное эгоистическое поведение
вступает в противоречие с коллективными интересами.
• Коллективные интересы диктуют выбор мирных стратегий. В то же
время, если игроки не обмениваются информацией, война является
наиболее вероятным исходом.
• (А1, В1)
- оптимальна по Парето. Однако эта ситуация
неустойчива, что ведет к возможности нарушения игроками
установленного соглашения. Действительно, если первый игрок
нарушит соглашение, а второй не нарушит, то выигрыш первого
игрока увеличится до трех, а второго упадет до нуля и, наоборот.
Причем, каждый игрок, не нарушающий соглашение, теряет
больше при нарушении соглашения вторым игроком, нежели в
том случае, когда они оба нарушают соглашение.
99
100. Способ определения оптимальных стратегий в биматричных играх
решаем матричную игру с матрицей платежей А.Находим из нее оптимальную смешанную
стратегию для игрока В и цену игры для игрока
А;
решаем матричную игру с матрицей B. Находим
из нее оптимальную смешанную стратегию для
игрока А и цену игры для игрока В.
100
101.
СПАСИБО ЗА ВНИМАНИЕ101


























































































 Менеджмент
Менеджмент








