Похожие презентации:
Условная оптимизация. Метод штрафных функций
1.
4.2. Метод штрафных функцийИдея метода заключается в преобразовании
условной задачи минимизации (4.1) – (4.3) в
задачу поиска безусловного минимума
вспомогательной функции
F ( x , rt ) f ( x ) P (rt , g k ( x)) ,
(4.25)
где P(rt , g k ( x)) - штрафная функция,
rt 0 - параметр штрафа, t 0, 1, .
Штрафная функция определяет наказание за
нарушение каждого из ограничений (4.2), (4.3) и таким
образом препятствует выходу точки из допустимой области.
2.
При выполнении ограничений штрафнаяфункция равна нулю.
В качестве штрафной функции, как правило,
используется функция следующего вида :
m
n
2
P(rt , g k ( x)) rt [ g k ( x)] [ g k ( x)]2 ,
k m 1
k 1
здесь g (x) - «срезка» функции g k (x) ,
определяемая следующим образом:
k
3.
g k ( x) , еслиg ( x)
если
0 ,
k
g k ( x) 0 ,
g k ( x) 0 .
(0)
x
За начальную точку поиска
можно принять любую
внешнюю точку, не удовлетворяющую ограничениям.
Для определения минимума вспомогательной функции
F ( x, rt ) решается последовательность задач t 0, 1, с
бесконечно возрастающим параметром штрафа rt .Для
организации итерационного процесса t 0, 1, может
быть использован любой численный метод безусловной
(t )
x
минимизации. Полученная точка
используется в
( 0)
(t )
x
x
качестве начальной точки
на следующей
итерации.
4.
Условие окончания процесса поискаP(rt , g k ( x ( t ) )) .
Метод штрафных функций относится к методу внешних
штрафных функций.
Пример 4.4. Решить задачу
f ( x) x1 x2 min ,
g1 ( x) x12 x2 0,
g 2 ( x) x1 0.
с точностью 0,01.
Решение. Составим вспомогательную функцию
2
2
(
x
)
2
1 , x1 0
F ( x, rt ) x1 x2 rt ( x 1 x2 )
.
x1 0
0,
5.
Решая задачу безусловной минимизацииметодом наискорейшего градиентного спуска для
возрастающей последовательности rt : 1, 2, 4, 16, ,
получим
x* (0,000975; - 0,000976) ,
f ( x * ) 0.
6.
4.3. Метод барьерных функцийВ данном методе предполагается, что
ограничения заданы в виде (4.3)
g k ( x) 0, k 1, m.
Идея метода состоит в том, что вдоль каждой
границы области ограничений устанавливается
«барьер». Следовательно, если поиск начинается из
внутренней точки, то минимум будет достигаться внутри
области ограничений.
Для формирования барьера используются следующие
типы штрафов:
7.
• штраф, задаваемый обратной функциейm
1
P(rt , g k ( x)) -rt
;
k 1 g ( x )
k
• логарифмический штраф m
P (rt , g k ( x)) -rt ln[ g k ( x)] .
k 1
Обе штрафные функции стремятся к бесконечности
при приближении к границе области изнутри.
x (0)
За начальную точку поиска
можно принять любую
внутреннюю точку, удовлетворяющую ограничениям.
8.
Для поиска минимума вспомогательной функции F ( x, rt )(4.25) решается последовательность задач t 0, 1,
с монотонно убывающей последовательностью rt . На
практике обычно эта последовательность рассчитывается
по рекуррентному соотношению
rt
rt 1 , t 0, 1, ,
C
где
r0 - начальное значение, обычно
C
выбирается r0 1, 10, 100 ;
- константа. Удачным может быть выбор
C 10, 12, 16.
9.
Поиск минимума функцииF ( x , при
rt )
заданном параметре
можно
проводить любым
rt
методом безусловной минимизации. Полученная
точка
используется в качестве начальной
(t )
x
точки
на следующей итерации.
( 0)
(t )
x окончания
x
Критерием
поиска служит неравенство
P (rt , g k ( x ( t ) ) .
Рассмотренный подход относят к методам
внутренних штрафных функций.
10.
Пример 4.6. Решить задачуf ( x) ( x1 4) 2 ( x2 - 4) 2 ,
g1 ( x) x1 x2 5 0.
при 0,01, r 0 100, c 10.
Решение. Составим вспомогательную функцию
F ( x, rt ) ( x1 4) 2 ( x2 4) 2 rt ln(5 x1 x2 ).
Решая задачу методом наискорейшего градиентного
спуска, получим
x* (2,499; 2,499).
F ( x* ; 0,001) 4,5.
11.
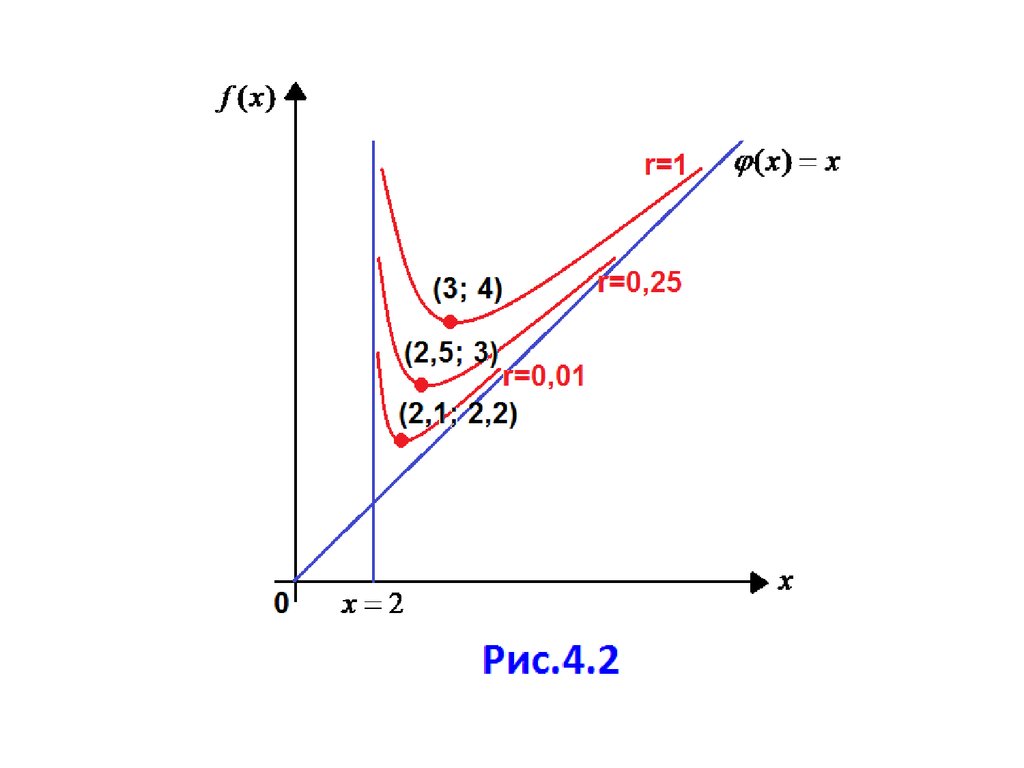
Пример 4.5. Используя штрафную функциюминимизировать функцию f (x) при ограничениях
x 2.
Перепишем ограничения в виде 2 x 0 .
Составим вспомогательную функцию
r
F ( x, rt ) x
.
2
(2 x)
На рис.4.2 изображен график функции F ( x, rt )
и показано положение точек ее минимума для
различных значений











 Математика
Математика Программирование
Программирование








