Похожие презентации:
Статистическая радиотехника (основы теории случайных процессов)
1. СТАТИСТИЧЕСКАЯ РАДИОТЕХНИКА (Основы теории случайных процессов)
Ведущие преподаватели:Грузман Игорь Семенович, профессор
кафедры ТОР, 4-415a
Мурасев Алексей Александрович,
ассистент кафедры ТОР, 4-413
2. СТРУКТУРА КУРСА
- 36 часов лекций,- 18 часов практических занятий,
(РТС – 36 часов)
- 18 часов лабораторных работ,
- 1 расчетно-графическое задание.
- Экзамен (2 вопроса, 1 задача)
3. ТЕМЫ ЛЕКЦИЙ
Случайные процессы и иххарактеристики.
Преобразование случайных процессов
в линейных стационарных системах .
Оптимальные и квазиоптимальные
линейные системы.
Основы теории обнаружения и
оценивания параметров сигналов.
4. ТЕМЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ И РГР
1.2.
3.
4.
5.
6.
7.
8.
Случайные величины и их характеристики.
Случайные процессы (СП) и их
характеристики. Самостоятельная работа (20
минут).
Стационарные и эргодические СП и их
характеристики.
Воздействие СП на линейные системы (ЛС).
К.Р. Воздействие СП на ЛС (2 часа).
Согласованный фильтр.
К.Р. Согласованный фильтр (2 часа).
Обнаружение детерминированных сигналов.
Сдать на проверку РГР на 12 неделе
5. ТЕМЫ ЛАБОРАТОРНЫХ РАБОТ
1.2.
3.
4.
Измерение характеристик СП.
Согласованный фильтр.
Изучение Винеровской фильтрации.
Подведение итогов.
6. ЭКЗАМЕН
К экзамену допускаются студенты, сдавшиелабораторные работы, защитившие РГР,
выполнившие программу практических занятий
Экзамен проводится в устном виде: предлагается
задача и два теоретических вопроса.
7. ЛИТЕРАТУРА
1.2.
3.
4.
5.
6.
7.
Грузман И.С. Основы теории случайных процессов.НГТУ,2004 г.
Грузман И.С. Применение теории случайных
процессов.- НГТУ,2006 г.
Борукаев Т.Б., Васюков В.Н., Грузман И.С. , Спектор
А.А. Применение статистических методов в
радиотехнике – НГТУ, 1992.
Липкин И.А. Статистическая радиотехника. Теория
информации и кодирования. – М.:Вузовская книга,
2002.
Левин Б.Р. Теоретические основы статистической
радиотехники. - М.: Сов. радио.
Тихонов В.И. Статистическая радиотехника. - М.:
Радио и связь
Шахтарин Б.И. Случайные процессы в радиотехнике. М.: Радио и связь, 2002 г.
8. Задачники
ЛИТЕРАТУРАЗадачники
1.
2.
Горяинов В.Т., Журавлев А.Г., Тихонов В.И.
Статистическая радиотехника: Примеры и
задачи. - М.: Сов. радио, 1980.
Гмурман В.Е. Руководство к решению задач по
теории вероятностей и математической
статистике. - М.: Высшая школа, 2000.
Лабораторные работы
Основы теории случайных процессов : метод.
указания к лаб. работам для 3 курса // А. А.
Спектор, И. С. Грузман . - Новосибирск : Изд-во
НГТУ, 2017.
9. ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ ОБРАБОТКИ СИГНАЛОВ
© Грузман И.С. Статистическая радиотехника, НГТУ, 201210.
РЕГИСТРАЦИЯ ИЗОБРАЖЕНИЙОдиночный элемент
Матрица чувствительных
элементов
(Гонсалес,Вудс,ЦОИ)
11. РЕГИСТРАЦИЯ ИЗОБРАЖЕНИЙ
12.
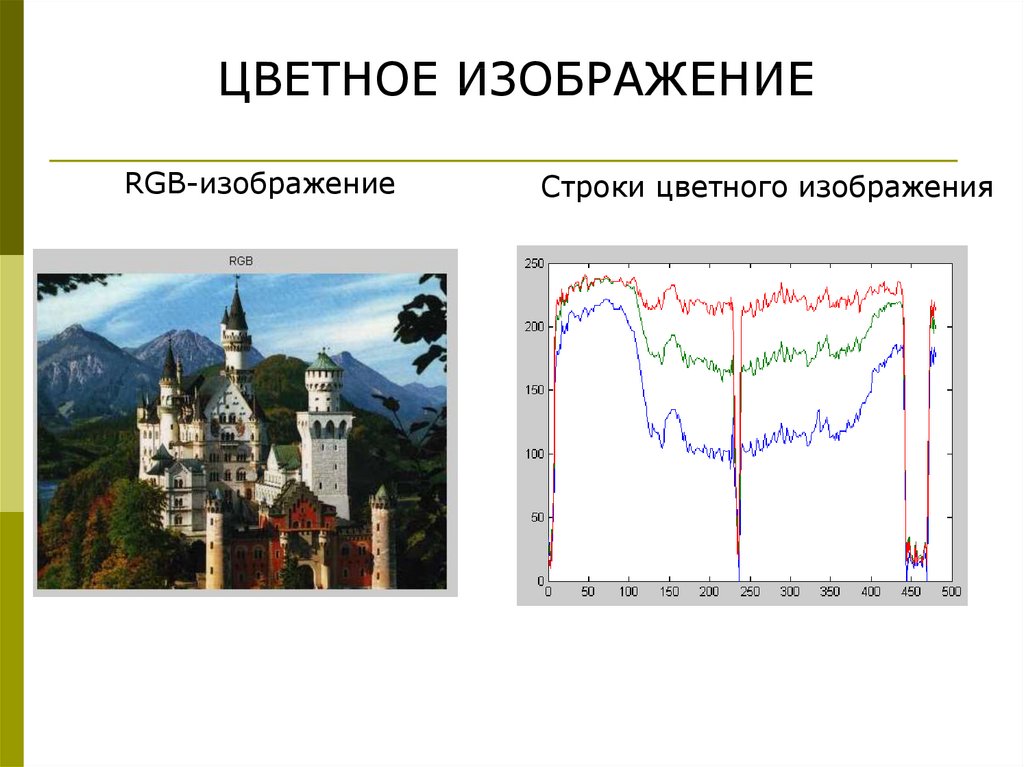
ЦВЕТНОЕ ИЗОБРАЖЕНИЕRGB-изображение
Строки цветного изображения
13. УЛУЧШЕНИЕ ВИЗУАЛЬНОГО КАЧЕСТВА ИЗОБРАЖЕНИЙ (ПРЕОБРАЗОВАНИЕ ГИСТОГРАММ)
y=f(x)w(x)
w(y)
14. ФИЛЬТРАЦИЯ СИГНАЛОВ (РАЗРАБОТКА МАГИСТРАНТА Д.С.КОЛМАКОВА И ИНЖЕНЕРА В.Н.ШАШКИНА -2008 Г.)
© Грузман И.С. Статистическая радиотехника, НГТУ, 201215.
МЕДИАННАЯ ФИЛЬТРАЦИЯИзображение, искаженное Результат линейной
фильтрации
импульсной помехой
© Грузман И.С. Статистическая радиотехника, НГТУ, 2012
Результат медианной
фильтрации
16.
ДИНАМИЧЕСКОЕ КВАНТОВАНИЕАЦП
y(i, j )
x(i, j )
z (i, j )
АЦП
m(i, j )
Оценка МО и
дисперсии
(i, j )
16
17.
ДИНАМИЧЕСКОЕ КВАНТОВАНИЕИсходное изображение
x(i, j )
Изображение, проквантованное
на 4 уровня без предварительной
обработки
Изображение, проквантованное
на 4 уровня с предварительной
обработкой
y(i, j )
z (i, j )
17
18. ДИНАМИЧЕСКОЕ КВАНТОВАНИЕ ТЕПЛОВИЗИОННЫХ ИЗОБРАЖЕНИЙ (магистрант Жданов М.В. – 2017)
Примеры засвеченныхтепловизионных изображений
Блок-схема работы алгоритма обработки
засвеченных тепловизионных кадров
18
19.
а)б)
19
a)
б)
а)Исходное незасвеченное изображение после преобразования 10 бит в 8
бит
б) Результат работы алгоритма обработки изображения а)
19
20.
ПОВЫШЕНИЕ ЧЕТКОСТИ ИЗОБРАЖЕНИЙМЕТОДОМ ВИНЕРОВСКОЙ ФИЛЬТРАЦИИ
(ФИЛЬТР ВИНЕРА)
© Грузман И.С. Статистическая радиотехника, НГТУ, 2012
21.
СВЕРХРАЗРЕШЕНИЕ22.
СВЕРХРАЗРЕШЕНИЕ23.
НЕПАРАМЕТРИЧЕСКИЕ АЛГОРИТМЫОБНАРУЖЕНИЯ ОБЪЕКТОВ
Исходное изображение
© Грузман И.С. Статистическая радиотехника, НГТУ, 2012
Результат обнаружения точки
пересечения двух лениаментов с
горизонтальной и вертикальной
ориентацией (крест)
24.
ПОСТРОЕНИЕ ПАНОРАМНЫХ ИЗОБРАЖЕНИЙ(ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛОВ)
(магистрант Никитин С.В. – 2008)
Исходные изображения
ПАНОРАМНОЕ ИЗОБРАЖЕНИЕ
© Грузман И.С. Статистическая радиотехника, НГТУ, 2012
25.
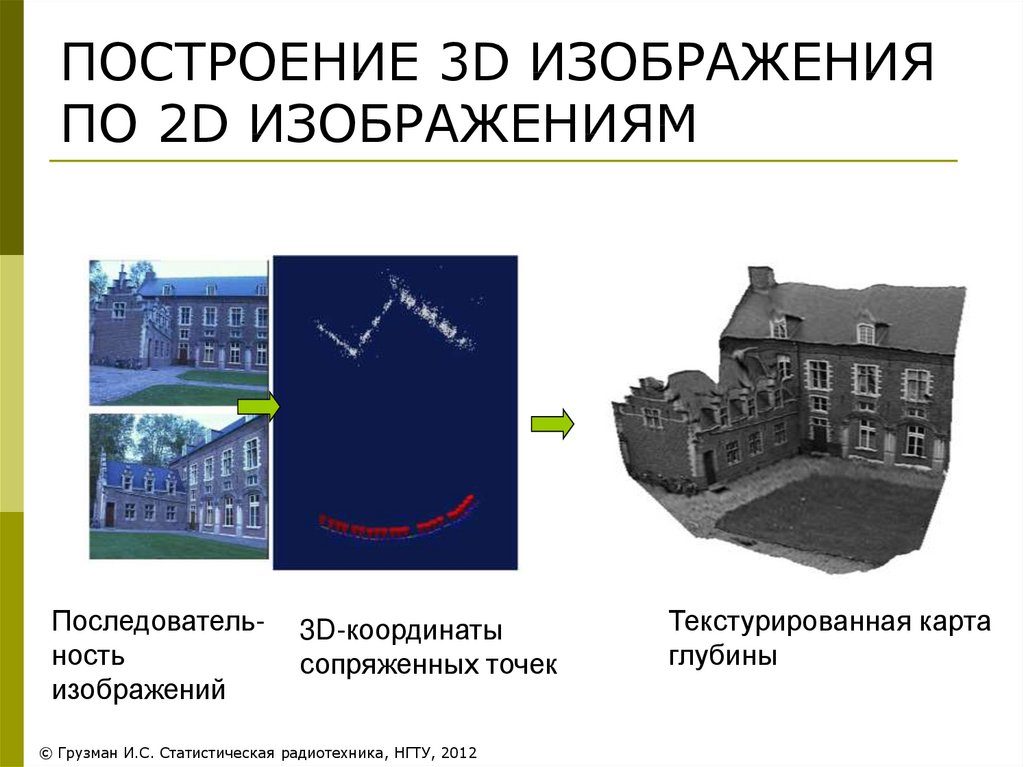
ПОСТРОЕНИЕ ТРЕХМЕРНЫХ ОБЪЕКТОВ26. ПОСТРОЕНИЕ 3D ИЗОБРАЖЕНИЯ ПО 2D ИЗОБРАЖЕНИЯМ
Последовательностьизображений
3D-координаты
сопряженных точек
© Грузман И.С. Статистическая радиотехника, НГТУ, 2012
Текстурированная карта
глубины
27. СЛУЧАЙНЫЕ ПРОЦЕССЫ. ОБЩИЕ ОПРЕДЕЛЕНИЯ
© Грузман И.С. Статистическая радиотехника, НГТУ, 201228. СЛУЧАЙНЫЕ ПРОЦЕССЫ. ОБЩИЕ ОПРЕДЕЛЕНИЯ
Случайный процесс X(t) – функция неслучайного аргумента t (времени),сечение которой является случайной величиной
Реализация СП X(t) - неслучайная функция x(t), в которую превращается
СП в результате опыта
Ансамбль – совокупность всех возможных реализаций СП
Случайный процесс – совокупность всех возможных реализаций вместе с
соответствующим распределением вероятностей появления этих реализаций
© Грузман И.С. Статистическая радиотехника, НГТУ, 2012
29. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ И ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СЛУЧАЙНОГО ПРОЦЕССА
Одномерная функция распределения (ФР) СП:F1 ( x1 ; t1 ) P ( X (t1 ) x1 )
Одномерная плотность распределения вероятностей (ПРВ) СП:
w1 ( x1; t1 ) F1 ( x1; t1 )
x1
ПРВ произвольного порядка :
wn ( x1 , ..., xn ; t1 , ..., tn )
Эквивалентные СП - процессы, у которых все конечномерные ПРВ совпадают
Дискретный белый шум - случайная последовательность с независимыми
сечениями :
n
wn ( x1 , ..., xn ; t1 , ..., tn ) w1 ( xi ; ti )
i 1
© Грузман И.С. Статистическая радиотехника, НГТУ, 2012
30.
ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ И ПЛОТНОСТЬРАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СЛУЧАЙНОГО
ПРОЦЕССА
Двумерная ФР:
Двумерная ПРВ:
F2 ( x1 , x2 ; t1 , t2 ) P( X (t1 ) x1; X (t2 ) x2 )
w2 ( x1 , x2 ; t1 , t2 )
© Грузман И.С. Статистическая радиотехника, НГТУ, 2012
2 F2 ( x1 , x2 ; t1 , t2 )
x1 x2
31. МОМЕНТНЫЕ ФУНКЦИИ СП
© Грузман И.С. Статистическая радиотехника, НГТУ, 201232. ТЕОРИЯ ВЕРОЯТНОСТЕЙ. НАЧАЛЬНЫЕ И ЦЕНТРАЛЬНЫЕ МОМЕНТЫ
Начальные моменты:mk M X k
mk M X k
x k w1 ( x)dx
n
k
x
i pi
i 1
Центральные моменты:
X X m1
k
k
M X
(
x
m
)
1 w1 ( x) dx
k M X m1
k
k
k M X
© Грузман И.С. Статистическая радиотехника, НГТУ, 2012
n
( x m1 )ik pi
i 1
33. ТЕОРИЯ ВЕРОЯТНОСТЕЙ. НАЧАЛЬНЫЕ И ЦЕНТРАЛЬНЫЕ МОМЕНТЫ
Смешанные начальныемоменты:
m1,1 M X1 X 2
x1 x2 w2 ( x1 , x2 )dx1dx2
Смешанные центральные моменты:
1,1 M X 1 X 2
( x1 m1, x1 )
© Грузман И.С. Статистическая радиотехника, НГТУ, 2012
( x2 m1, x2 ) w2 ( x1 , x2 )dx1dx2
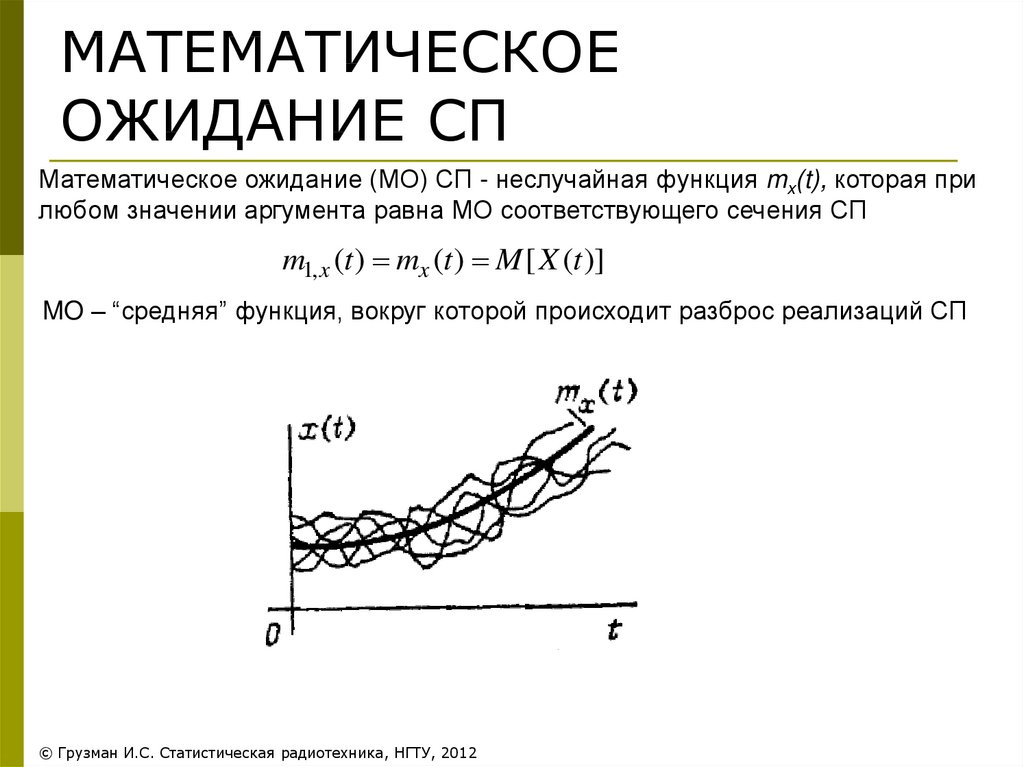
34. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ СП
Математическое ожидание (МО) СП - неслучайная функция mx(t), которая прилюбом значении аргумента равна МО соответствующего сечения СП
m1, x (t ) mx (t ) M [ X (t )]
MO – “средняя” функция, вокруг которой происходит разброс реализаций СП
© Грузман И.С. Статистическая радиотехника, НГТУ, 2012
35. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
m1 40m1 120
m1 200
36.
СВОЙСТВА МО СПm1, x (t ) mx (t ) M [ X (t )]
1.
M [ (t )] (t )
2. M [ (t ) X (t )] (t ) mx (t )
3.
M [ (t ) X (t )] (t )mx (t )
4.
5. Для независимых СП:
M [ X (t ) Y (t )] mx (t ) my (t )
M [ X (t ) Y (t )] mx (t ) my (t )
Начальная моментная функция второго порядка :
m2, x (t ) M [( X (t ))2 ]
ПРИМЕР
Найти МО СП X(t)=Ucos(5t), где U – случайная величина, равномерно
распределенная на интервале [1,5]
mx (t ) M [ X (t )] M [U cos(5t )] M [U ] M [cos(5t )] 3cos(5t )
© Грузман И.С. Статистическая радиотехника, НГТУ, 2012
37. ЦЕНТРИРОВАННЫЙ СП. ДИСПЕРСИЯ СП
Центрированный СП:X (t ) X (t ) m x (t )
1.
M [ X (t )] 0
2. Прибавление к СП неслучайной функции не изменяет ЦСП:
Y (t ) X (t ) (t ) Y (t ) X (t )
3. Y (t ) (t ) X (t )
Дисперсия СП:
Y (t ) (t ) X (t )
Dx (t ) D[ X (t )] M [( X (t ))2 ]
Dx (t ) M [( X (t ) mx (t ))2 ] m2, x (t ) mx2 (t )
Среднеквадратическое отклонение:
© Грузман И.С. Статистическая радиотехника, НГТУ, 2012
x (t ) Dx (t )
38. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
x Dxm1 120 19
m1 120
38
m1 120
57



































 Электроника
Электроника








