Векторы в пространстве

1.

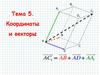
B1
A1
ТЕМА:
D1
Векторы в
пространстве.
Записать
конспект с
презентации
C1
B
A
C
D
AC1 AB AD AA1

2.

I. Определение вектора. Основные понятия, связанные с векторами.
Как и в плоскости, в пространстве вектор определяется как направленный
отрезок:
B
A
Точка А – начало вектора, В – конец вектора. Записывают:
AB
или
a.
Обычную точку в пространстве мы также можем считать вектором, у которого
начало совпадает с конечной точкой. Такой вектор называется нулевым и
обозначается: 0 или AA .
0
A
Длина отрезка, изображающего вектор, называется модулем (или абсолютной
величиной) вектора, т.е.
AB AB åä.î ò ð. .
Естественно, что
B
AA 0.
Векторы AB и BA являются
противоположными. Очевидно, что:
AB BA .
A

3.

Два вектора называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых:
Коллинеарные векторы, в свою очередь, бывают одинаково направленными (или
соноправленными) и противоположно направленными. В нашем случае:
a ↑↑ c
– соноправленные векторы,
a ↑↓ b , c ↑↓ b
– противоположно
направленные векторы.
Два вектора называются равными, если: 1) они соноправлены; и 2) их модули
равны, т.е.
a b a ↑↑ b è a b
a
b

4.

От произвольной точки пространства можно отложить единственный вектор,
равный данному:
N
a
a MN
M
Три вектора называются компланарными, если они лежат в одной плоскости:
b
a
c
Углом между векторами называется угол между их направлениями:
a
b
a,b
Величина угла между векторами может изменятся от 00 до 1800. Подумайте, когда:
а) a,b 0 и б) a,b 1800 ?
0
Ответ: а)
a ↑↑ b ;
б)
a ↑↓ b
.

5.

II. Действия с векторами.
Векторы можно складывать – в результате получается вектор. При сложении двух
векторов применяются правила треугольника или параллелограмма:
1) При применении правила треугольника один из векторов откладывают от конца
другого, т.е. MK KF MF :
a b
a
b
2) При применении правила параллелограмма оба вектора откладывают из общей
начальной точки, т.е. MK MN MF , где F – вершина параллелограмма,
противоположная общей начальной точке векторов.
a b
a
b

6.

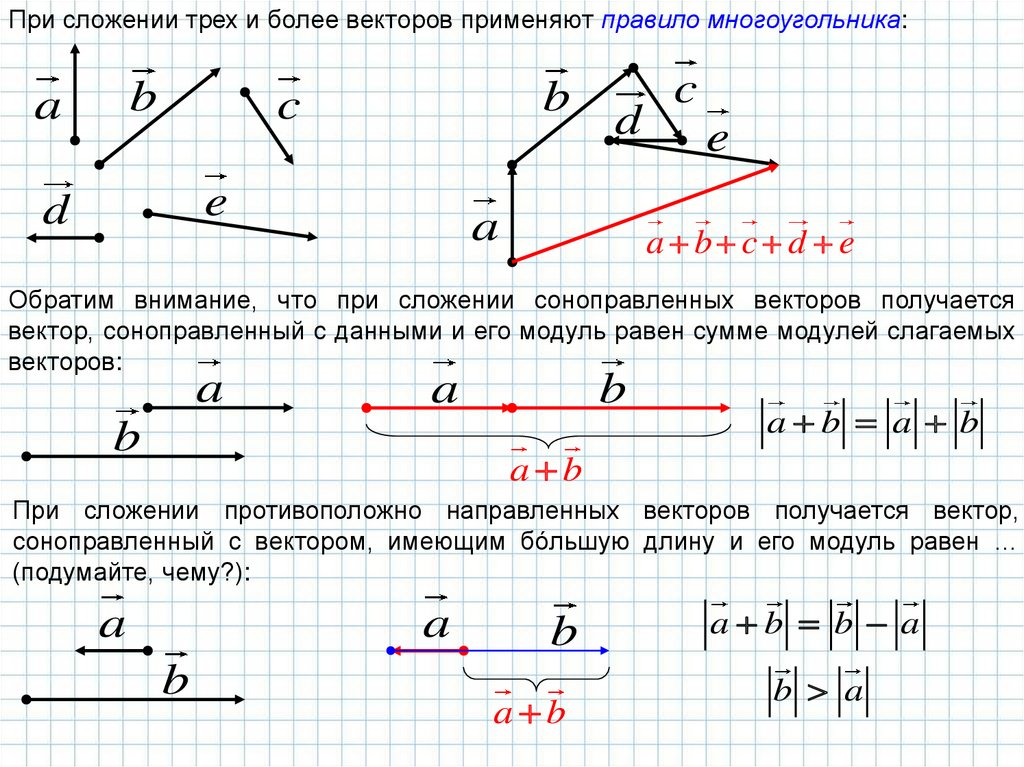
При сложении трех и более векторов применяют правило многоугольника:
b
a
b
c
e
d
d
a
c
e
a b c d e
Обратим внимание, что при сложении соноправленных векторов получается
вектор, соноправленный с данными и его модуль равен сумме модулей слагаемых
векторов:
a
a
b
b
a b a b
a b
При сложении противоположно направленных векторов получается вектор,
соноправленный с вектором, имеющим бóльшую длину и его модуль равен …
(подумайте, чему?):
a
a
b
b
a b
a b b a
b a

7.

Также можно найти разность двух векторов – в результате получается вектор. При
вычитании двух векторов применяется видоизмененное правило треугольника –
вначале оба вектора строятся с общей начальной точкой, затем соединяются
концы этих векторов с выбором направления к «уменьшаемому» вектору:
b
a
a b
Или: т.к. a b a b
, то можно вначале построить вектор, противоположный
вектору b , а затем оба вектора сложить по правилу треугольника.
a
–
b
a b

8.

Сложение векторов, как и сложение чисел подчиняется законам:
1)
a b b a
2)
a b c a b c – сочетательный закон сложения;
– переместительный закон сложения;
a 0 a ;
4) a a 0 .
3)
Следующее действие с векторами – умножение вектора на число k. В результате
этого действия получается вектор, причем:
1) если k>0, то
2) если k<0, то
k a ↑↑ a
k a ↑↓ a
ka k · a ;
и ka k · a ;
и
3) если k=0, то 0 ·a 0 .
a
8
a
3
0·a
3a
2a
4
a
3