Похожие презентации:
Векторы в пространстве
1.
2.
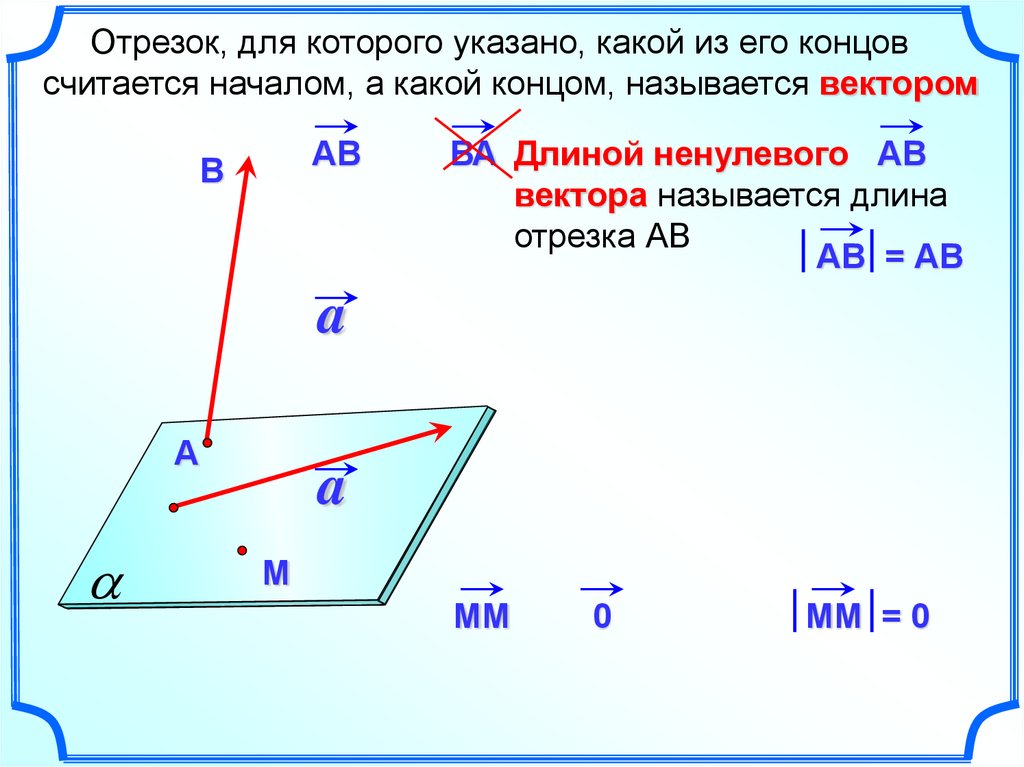
Отрезок, для которого указано, какой из его концовсчитается началом, а какой концом, называется вектором
АВ
В
ВА Длиной ненулевого АВ
вектора называется длина
отрезка АВ
АВ = АВ
a
А
a
M
MM
0
MM = 0
3.
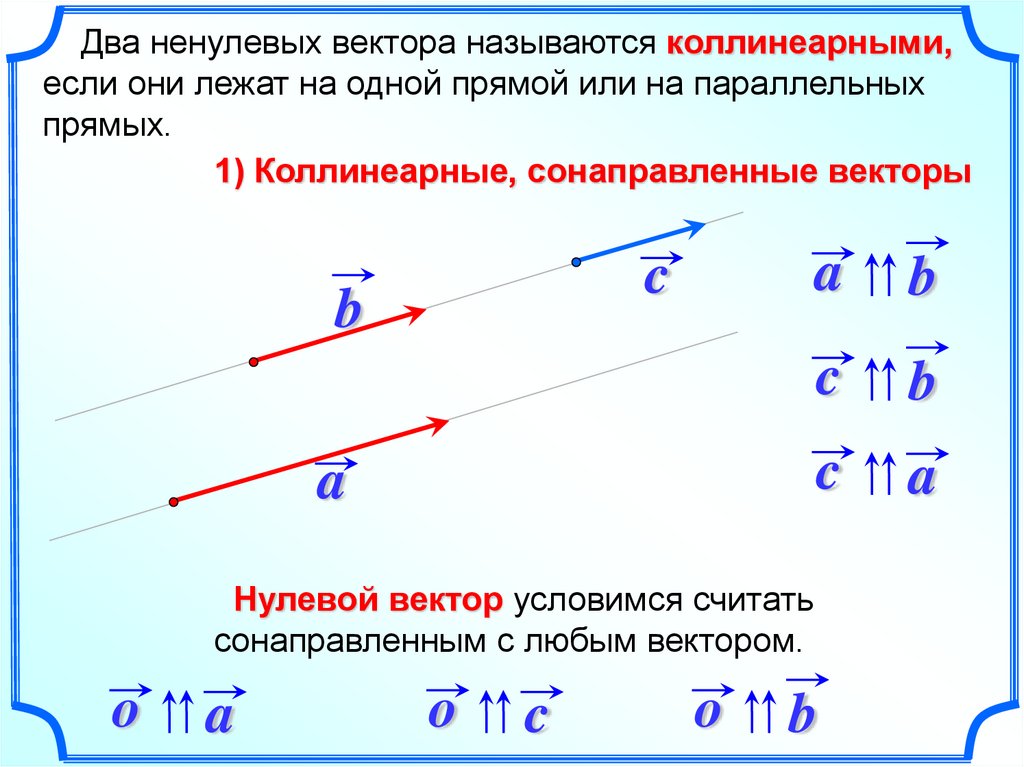
Два ненулевых вектора называются коллинеарными,если они лежат на одной прямой или на параллельных
прямых.
1) Коллинеарные, сонаправленные векторы
c
b
a
a
b
c
b
c
a
Нулевой вектор условимся считать
сонаправленным с любым вектором.
o
a
o
c
o
b
4.
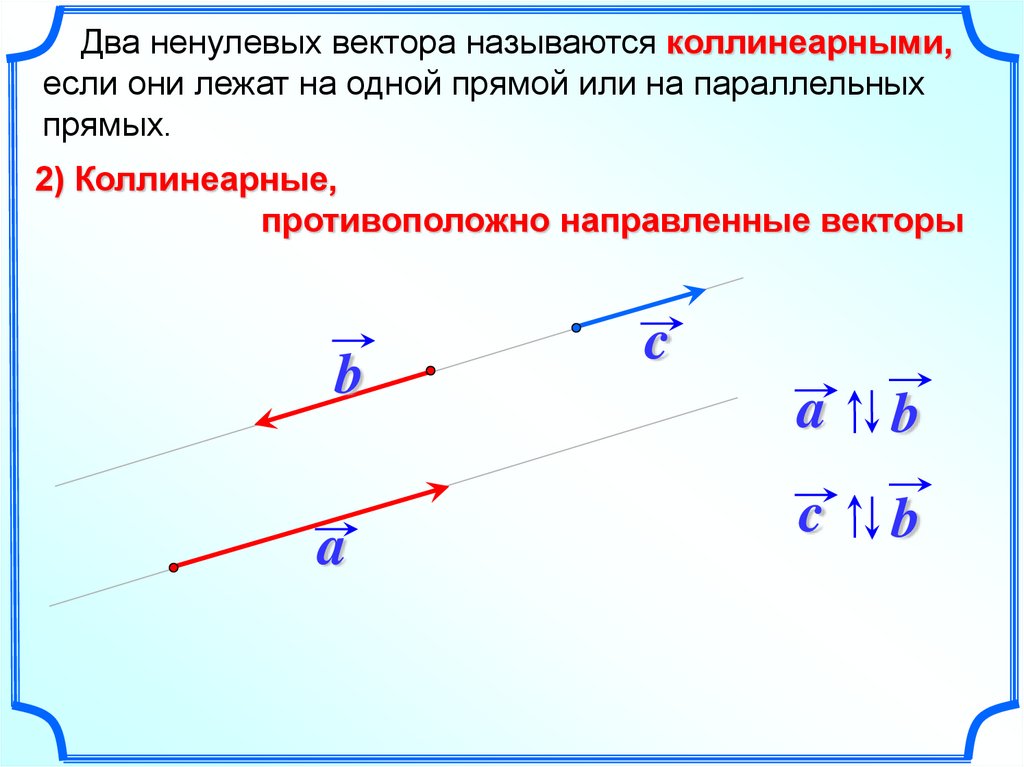
Два ненулевых вектора называются коллинеарными,если они лежат на одной прямой или на параллельных
прямых.
2) Коллинеарные,
противоположно направленные векторы
b
a
c
a
b
c
b
5.
Многие физические величины, например силаперемещение, скорость, являются векторными
величинами. При изучении электрических и магнитных
явлений появляются новые примеры векторных величин.
Электрическое поле,
создаваемое в
E
пространстве зарядами,
характеризуется в каждой
точке пространства
вектором напряженности
+
электрического поля.
На рисунке
изображены векторы
напряженности
электрического поля
положительного точечного
заряда.
6.
Направление токаB
Электрический ток, т.е.
направленное движение
зарядов, создает в
пространстве магнитное
поле, которое
характеризуется в каждой
точке пространства
вектором магнитной
индукции.
На рисунке
изображены векторы
магнитной индукции
магнитного поля прямого
проводника с током.
7.
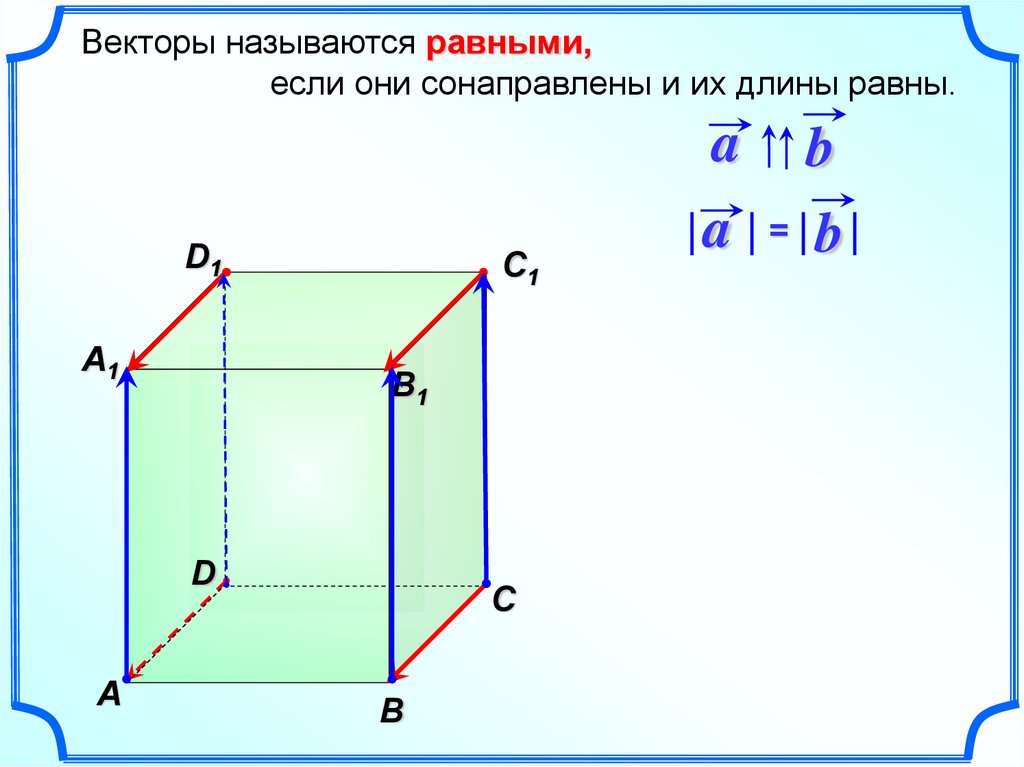
Векторы называются равными,если они сонаправлены и их длины равны.
a
D1
A1
C1
B1
D
A
C
B
a
b
=
b
8.
АВСDH – правильная четырехугольная пирамида.Верно ли равенство векторов?
DA = CB
Н
CD = BA
HC = HA
CO = OA
OD = OB
D
С
O
А
В
9.
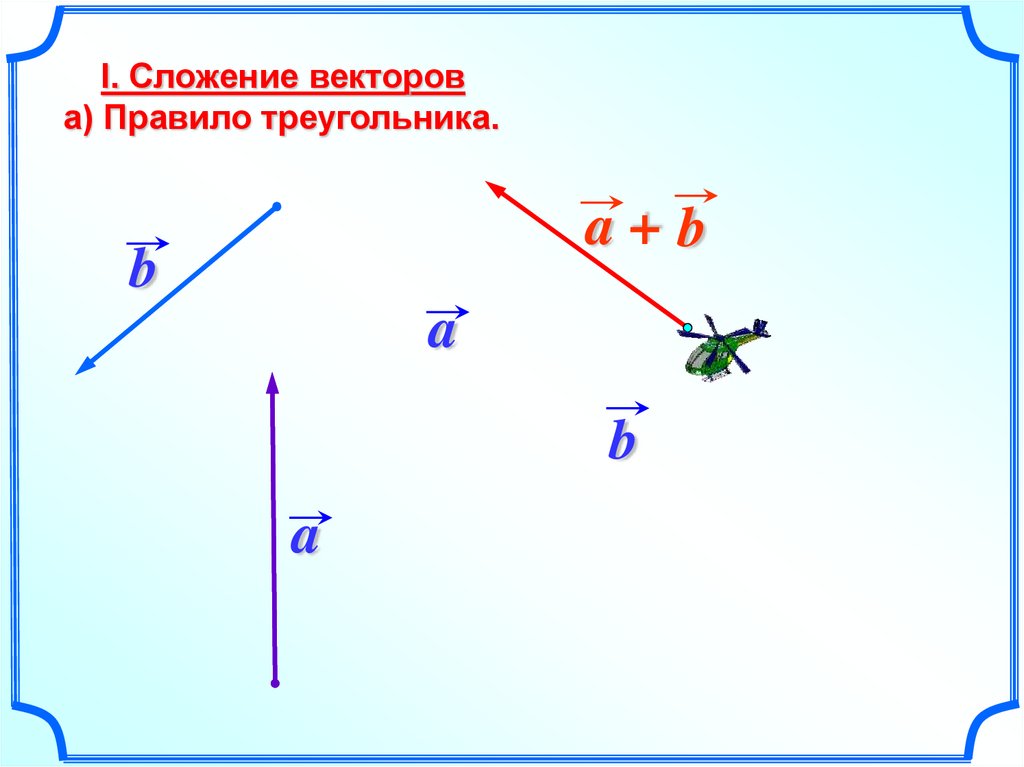
I. Сложение векторова) Правило треугольника.
a+b
b
a
b
a
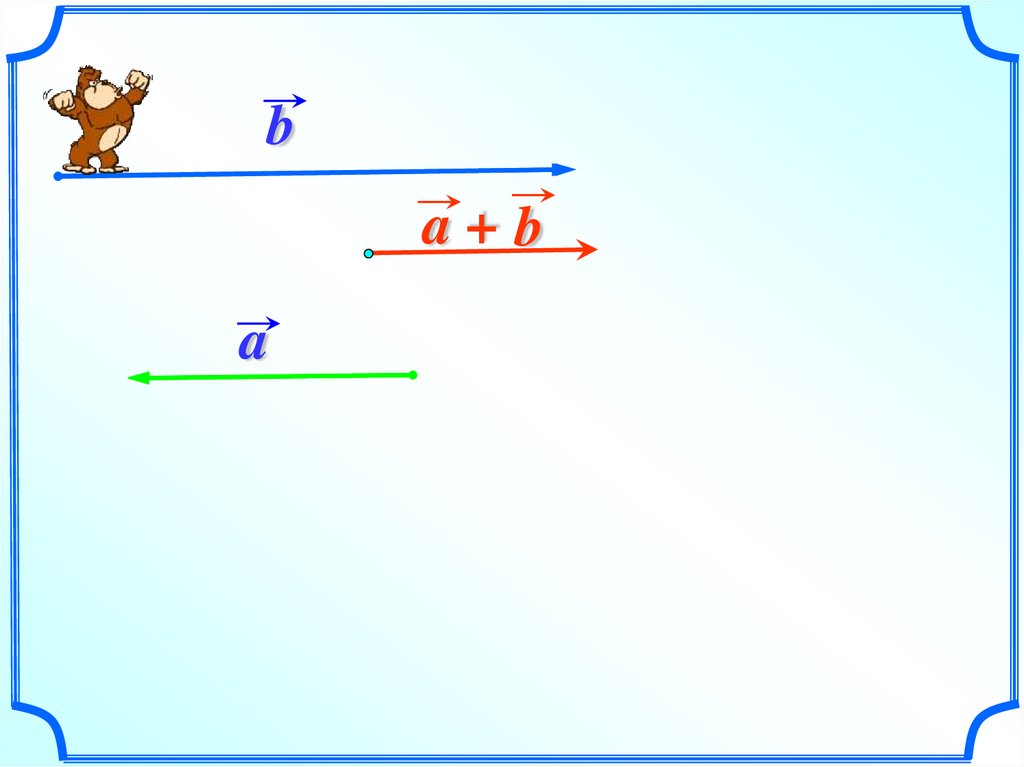
10.
По правилу треугольника складываются иколлинеарные векторы, хотя при их сложении
треугольника и не получается
b
a+b
a
b
a
11.
ba+b
a
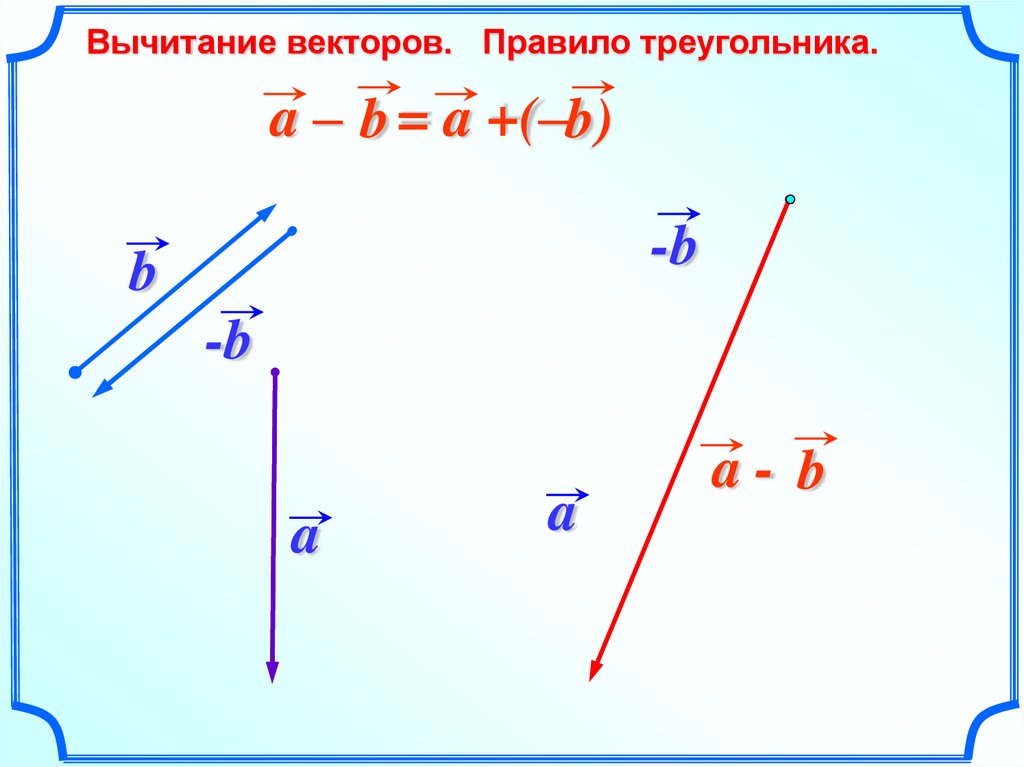
12.
Вычитание векторов. Правило треугольника.a – b = a +(–b)
-b
b
-b
a
a
a- b
13.
Сложение векторов. б) Правило параллелограмма.a+b
b
b
a+b
a
a
14.
Сложение векторов.Правило треугольника.
АВ + ВС = АС
АО + ОР = АР
MN + NR = MR
MK + KM = MM = 0
MK + OM = OM + MK = OK
MF - SF =
MF + FS = MS
RO - RM = RO + MR = MR + RO = MO
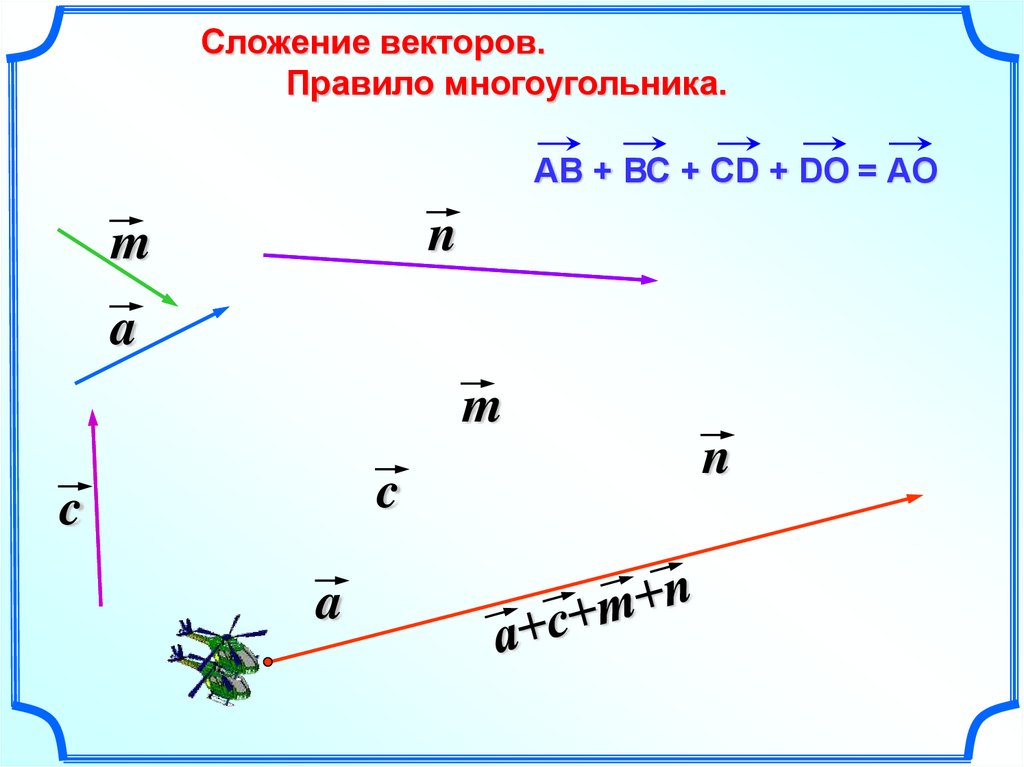
15.
Сложение векторов.Правило многоугольника.
АВ + ВС + СD + DO = АO
n
m
a
m
c
c
a
n
16.
Сложение векторов.Правило многоугольника.
А1A2+ A2A3+ A3 A4 + A4A5 +A5A6 +A6A7 = А1A7
A1
A5
A6
A7
A4
A2
A3
17.
kaУмножение вектора на число.
b
2b
a
2b b
2b = 2 b
1
a
2
1
a
2
1
a
2
a
=
1
2
a
18.
Умножение вектора на число.Произведением ненулевого вектора
a
на число
k
b, длина которого равна k a ,
причем векторы a и b сонаправлены при k>0 и
противоположно направлены при k<0.
называется такой вектор
k









 Математика
Математика








