Похожие презентации:
Термоэлектрические и термомагнитные явления. Диффузионный ток
1. Лекция 7. Термоэлектрические и термомагнитные явления. Диффузионный ток.
Эффект Холла. Тензор магнитосопротивления. Холловскаяподвижность.
Квантование электронов и дырок в сильном магнитном
поле. Уровни Ландау.
Циклотронный резонанс. Квантовый эффект Холла.
2. Эффект Холла
В 1879 году, американский физик Э. Холл обнаружил, что если к образцу, покоторому течёт электрический ток, приложить перпендикулярно этому току
магнитное поле, то в направлении, ортогональном направлению тока и
направлению магнитного поля возникает напряжение, пропорциональное току,
протекающему через образец.
Сила Лоренца
Условие равновесия:
q
q E H vd B 0
c
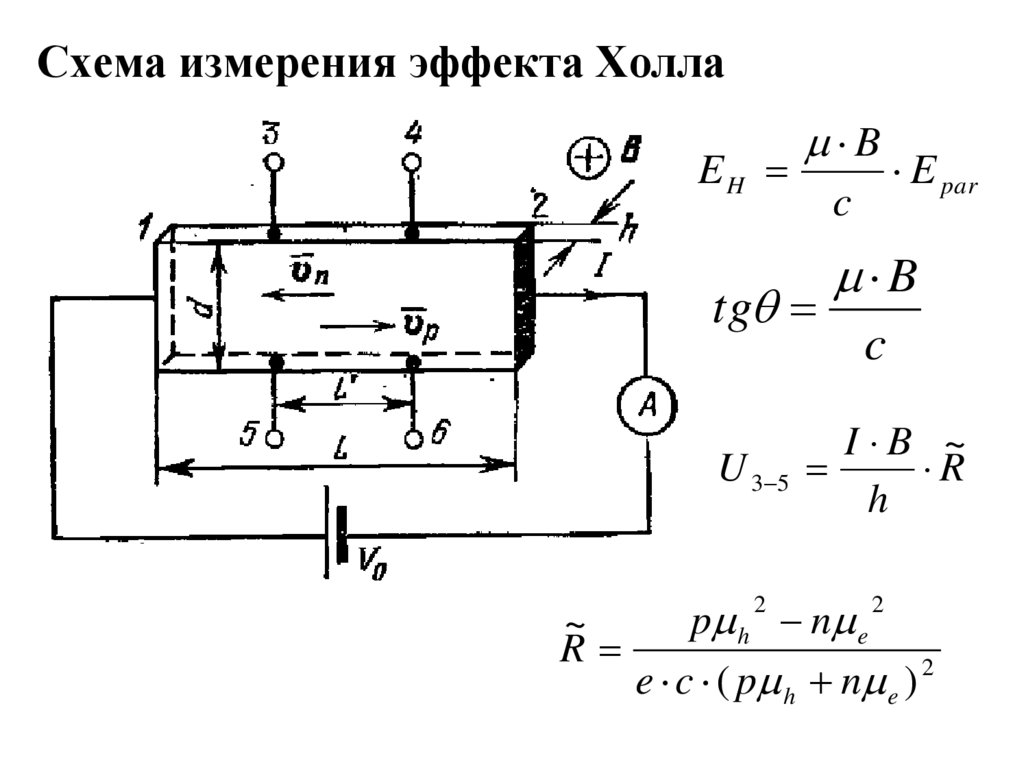
3. Схема измерения эффекта Холла
EHB
c
tg
U 3 5
~
R
E par
B
c
I B ~
R
h
p h n e
e c ( p h n e ) 2
2
2
4.
По знаку Холловского напряжения можноопределить знак основного типа носителей
заряда.
Зная геометрию образца, можно определить
Холловскую подвижность.
Измерив удельное сопротивление, можно
определить концентрацию носителей
заряда.
Датчики Холла – измерения магнитного
поля, измерения частоты вращения.
5. Тензор магнетосопротивления, квантовый эффект Холла
j Ee B
c
mc
c kT
Циклотронная частота, если, c
то возможно поглощение
ЭМ при переходе на
следующий уровень
«квантующие» магнитные поля
1
квантование в магнитном поле, уровни Ландау
Квантовый эффект Холла (Нобелевская премия, фон
Клитцинг с коллегами)
Двумерный электронный газ, фактор заполнения.
При целочисленном факторе заполнения U3-4=0, а
отношение Холловского напряжения к току было кратно
кванту сопротивления (25813 Ом).
6. Диффузионный ток
Диффузия. Соотношение Эйнштейна.Неравновесные носители заряда. Время жизни
неравновесных носителей заряда. Амбиполярная
диффузия.
Термоэлектрические и термомагнитные явления.
Связь плотности тока и градиента квазиуровня
Ферми в полупроводниках.
7. Соотношение Эйнштейна
nДиффузионный ток
j x, d e D
x
Связь коэффициента диффузии
и длины свободного пробега
Соотношение
Эйнштейна:
2
1
D vT
3
D 1 lvT
3
kT
kT
m*
e
m*vT 2 3
kT
2
2
Диффузия неравновесных носителей заряда (генерация
фотонами, инжекция). Амбиполярная диффузия.
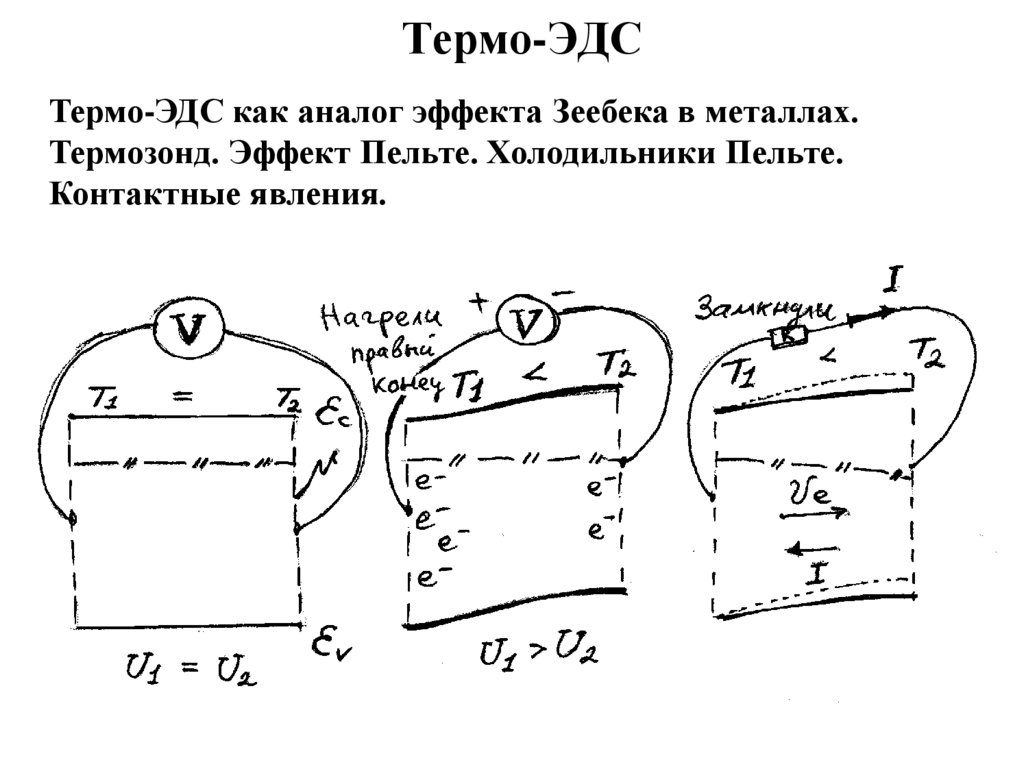
8. Термо-ЭДС
Термо-ЭДС как аналог эффекта Зеебека в металлах.Термозонд. Эффект Пельте. Холодильники Пельте.
Контактные явления.
9. Термомагнитные явления
Поперечный эффект Нернста-Эттингсгаузена.Аналог эффекта Холла. Влияние знака носителей
заряда на знак эффекта.
10. Связь плотности тока и градиента квазиуровня Ферми в полупроводниках
nkT
n
j x E x eD
en E x e
x
e
x
c
n
j x n
kT
x
x n N C e
c
Nc
j x n
kT
e
x
kT
f c
kT
- ток для
электронов
f c в невырожденном
полупроводнике
kT
( f c )
f
n
x
x
Ток пропорционален градиенту уровня
Ферми, концентрации и подвижности!!!
11. Классификация времён релаксации в полупроводниках
1) Время релаксации по энергии (время«термализации»). Электронная и фононная
температура.
2) Время релаксации по импульсу.
3) Время жизни неравновесных носителей заряда.
Рекомбинация носителей заряда в прямозонных и
непрямозонных полупроводниках.









 Физика
Физика Электроника
Электроника








