Случайные величины. Центральные тенденции меры разброса

1. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ЦЕНТРАЛЬНЫЕ ТЕНДЕНЦИИ МЕРЫ РАЗБРОСА

2.

1. Относительной частотой
события А в данной серии
испытаний называют
отношение числа
испытаний М, в которых
это событие произошло, к
числу всех проведенных
испытаний N.

3.

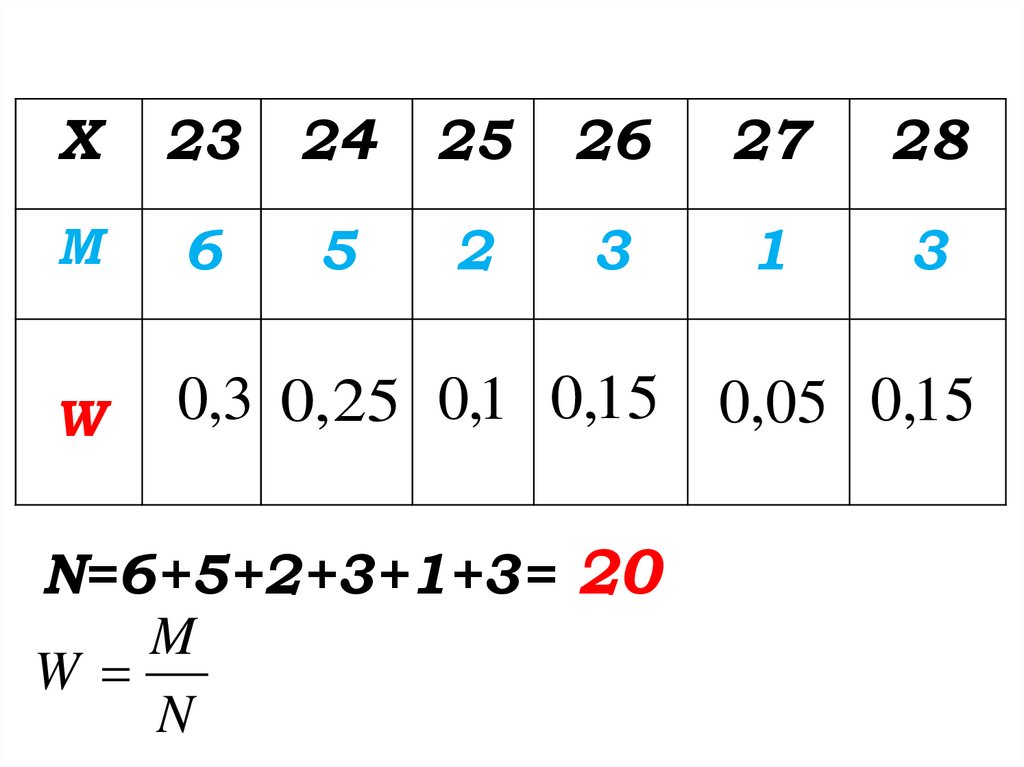
X
23
24
25
26
27
28
М
6
5
2
3
1
3
W
0,3 0,25 0,1 0,15 0,05 0,15
N=6+5+2+3+1+3= 20
M
W
N

4.

2. Число испытаний М
называют частотой
события А.

5.

3. Относительную частоту
события А обозначают
W ( А)

6.

4.
M
W ( А)
N
W (А) относительная частота
события
А в данной серии испытаний
М число испытаний
(частота события
А)
N число всех проведенных
испытаний

7.

Обследуемая совокупность
называется генеральной
совокупностью

8.

Значительная часть
генеральной совокупности,
выбранная случайным образом,
называется выборкой

9.

Если в выборке присутствуют
все значения случайной величины
примерно в тех же пропорциях,
что и в генеральной
совокупности, то эту выборку
называют
репрезентативной

10.

11.

«Размах и центральные
тенденции»

12.

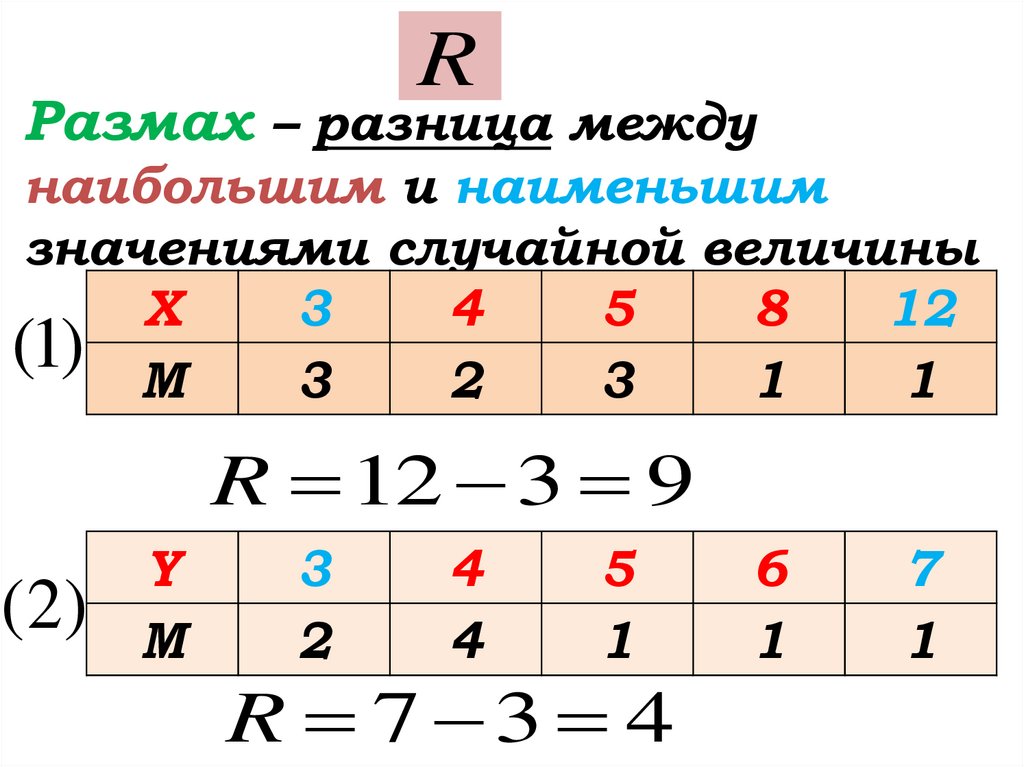
R
Размах – разница между
наибольшим и наименьшим
значениями случайной величины
X
3
4
5
8
12
(1) M
3
2
3
1
1
R 12 3 9
( 2)
Y
M
3
2
4
4
5
1
R 7 3 4
6
1
7
1

13.

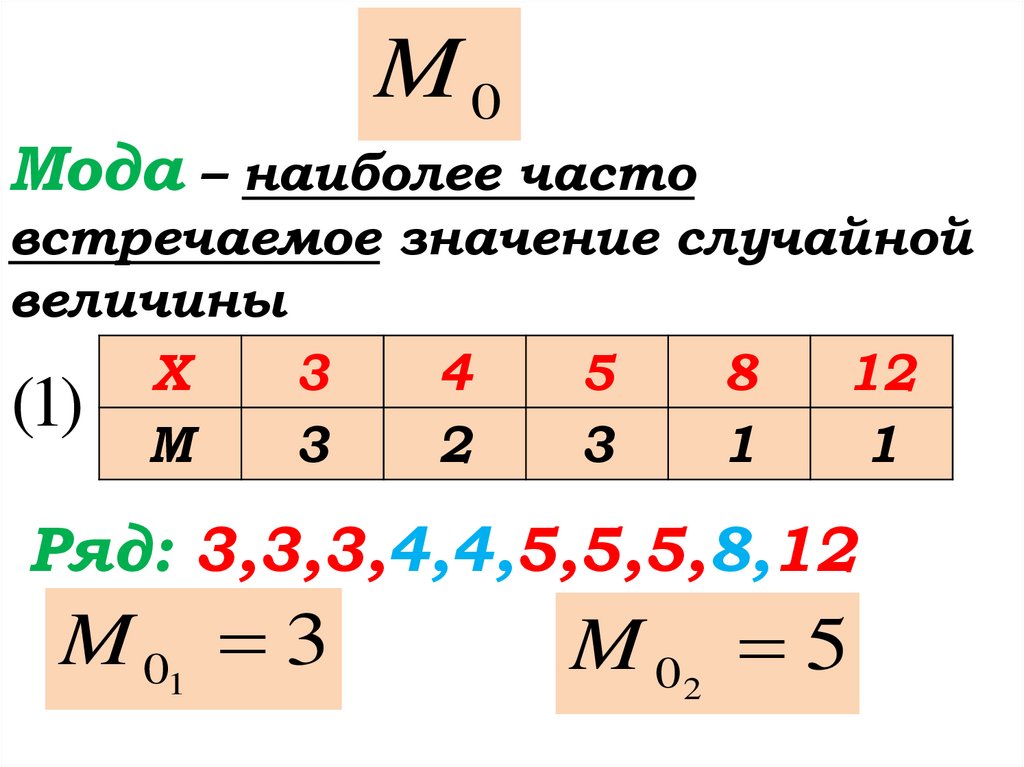
M0
Мода – наиболее часто
встречаемое значение случайной
величины
X
3
4
5
8
12
(1)
M
3
2
3
1
1
Ряд: 3,3,3,4,4,5,5,5,8,12
M 01 3
M 02 5

14.

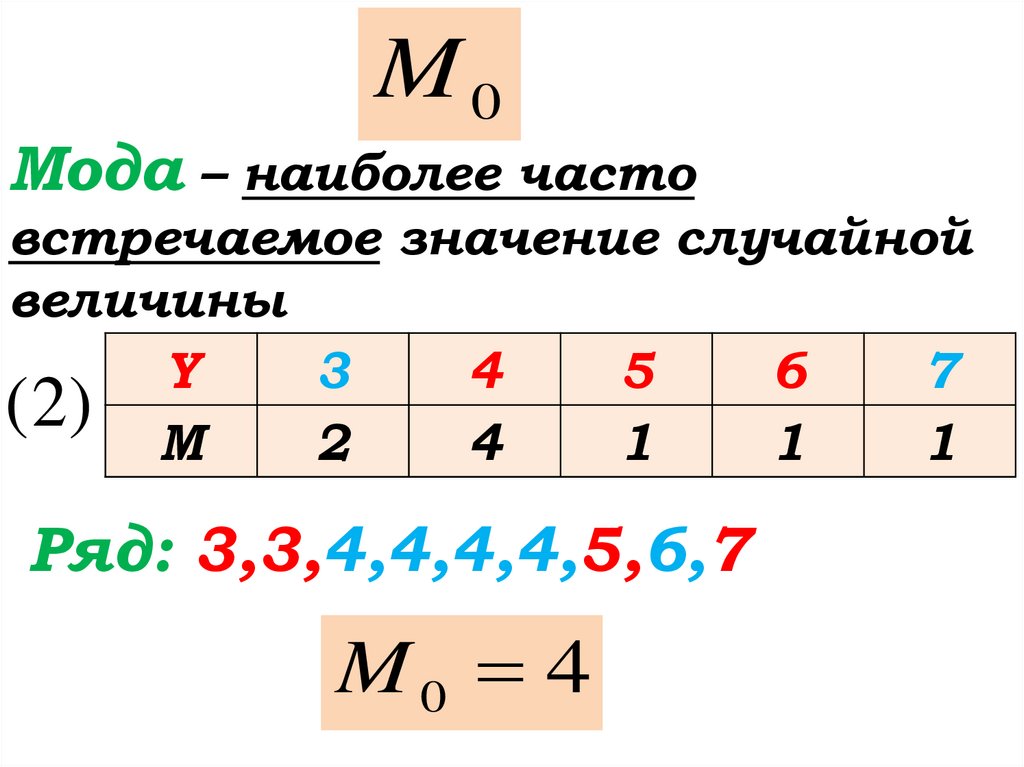
M0
Мода – наиболее часто
встречаемое значение случайной
величины
Y
3
4
5
6
7
( 2) M
2
4
1
1
1
Ряд: 3,3,4,4,4,4,5,6,7
M0 4

15.

Me
Медиана – это так
называемое серединное
значение упорядоченного ряда
значений случайной величины
… 5,5,5,8,12
4 5
Me
4,5
2
(1): 3,3,3,4, 4

16.

Me
Медиана – это так
называемое серединное
значение упорядоченного ряда
значений случайной величины
(2): 3,3,4,4, 4 4,5,6,7
Me 4

17.

Медиана – это так называемое
серединное значение упорядоченного
ряда значений случайной величины
Вывод: Если число чисел
упорядоченного ряда:
чётное, то M e среднему
арифметическому двух
центральных значений;
нечётное, то M e значению
среднего центрального ряда

18.

19.

1) R 6 ( 1) 7
2) Упорядоченный ряд чисел:
-1,-1,2,2,2,3,3,3,3,5,5,5,5,6
M 01 3;
3)
Me 3
M 02 5

20.

Стр.161, №405(1)
а) Упорядоченный ряд:
1; 2; 3; 3; 4; 4.
R 4 ( 2) 6
M 0 2
-2; -2; -2; 0; 1;
б)
в)
г)
Mе 1

21.

22.

3 4 1 2 5
1) Х
3
5
2 5 4 3 2 1
2) Х
0,5
6
2 2 3 3 3 5 5
1
3) Х
2
7
7
4 3 5 2 6 3
4) Х
5
8