Похожие презентации:
Уравнения окружности, сферы, плоскости
1. Задание:
1.Изучить материал,2. составить опорный конспект,
3. выучить формулы,
4. отправить конспект на проверку.
Подготовила: преподаватель математики
Филимонова Ольга Николаевна
ГОУ НПО «Профессиональный лицей №13»
г.Калуга, 2008 г.
далее
2. Эпиграф к уроку:
“Предмет математики настолько серьёзен,Что полезно не упускать случаев
Делать его немного занимательным”.
О. Паскаль
3. Содержание моей презентации:
ЦилиндрКонус и усечённый конус
Шар и сфера
4.
Тела вращенияцилиндр
назад
конус
шар
далее
5. Цилиндр
ОпределениеТело, состоящее из двух кругов,
совмещаемых параллельным переносом и всех отрезков,
соединяющих соответствующие точки этих кругов.
Способ образования
Вращением прямоугольника вокруг одной из сторон
прямоугольника или вокруг оси симметрии прямоугольника.
На начало
далее
6.
Виды цилиндровПрямой(круговой)
назад
Наклонный
далее
7. Круговой прямой цилиндр
8. Наклонный цилиндр
Наклонный цилиндр– цилиндр,
образующие
которого не
перпендикулярны
плоскостям его
оснований.
9. Элементы цилиндра
AR
.O1
Образующая-AB (AB=L)
Радиус основания-R (R=O1A=O2B)
Высота-H (O1O2=H)
L
B
назад
.F
.O2
L
Основания цилиндра- круги с
центрами О1 и О2
Ось цилиндра- прямая О1О2
Центр симметрии- точка F
(середина отрезка О1О2)
далее
10. Свойства цилиндра
Основания цилиндра равны.Основания лежат в параллельных
плоскостях.
Образующие параллельны и равны.
назад
далее
11.
Развёртка цилиндрапрямоугольник
2 круга
R
H
назад
2ПR
далее
12.
Сечение цилиндра плоскостью•Сечение цилиндра плоскостью,
параллельной оси цилиндра –
прямоугольник
•Осевое сечение – прямоугольник
.
.
назад
.
.
.
•Сечение цилиндра
плоскостью,
перпендикулярной
оси цилиндра – круг
далее
13. Формулы
Площадь боковой поверхностицилиндра
Площадь полной
поверхности
цилиндра
Объём цилиндра
назад
S=2ПRH
S=2ПRH+2ПR2
V=SоснH=ПR2H
На начало
14. Конус
•ОпределениеТело, состоящее из круга – основания конуса,
точки, не лежащей в плоскости этого круга,
- вершины конуса и всех отрезков, соединяющих
вершину конуса с точками основания-образующими
•Способ образования
Вращением прямоугольного треугольника
вокруг своего катета как оси
На начало
далее
15.
Элементы конусам
Точка М- вершина
Отрезок МА=L - образующая
Отрезок МО=Н- высота
Отрезок ОА=R- радиус
основания
Отрезок АВ=2R- диаметр
основания
Круг с центром Ооснование
назад
А
R
о
В
далее
16. Прямой круговой конус
17.
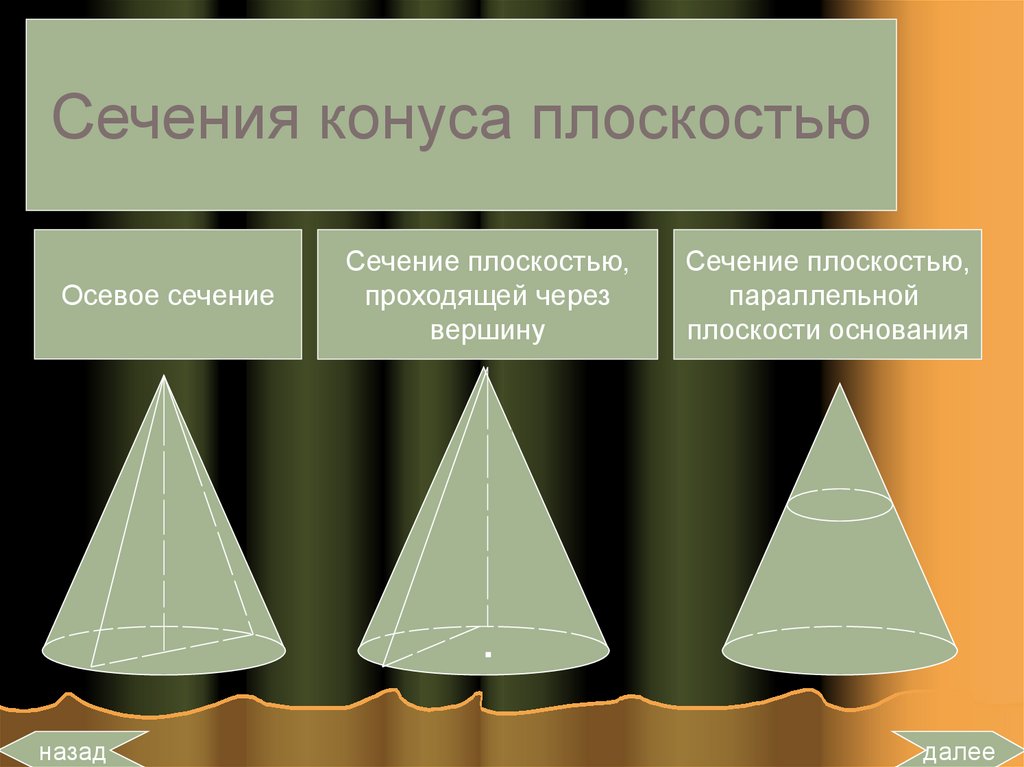
Сечения конуса плоскостьюОсевое сечение
Сечение плоскостью,
проходящей через
вершину
Сечение плоскостью,
параллельной
плоскости основания
.
назад
далее
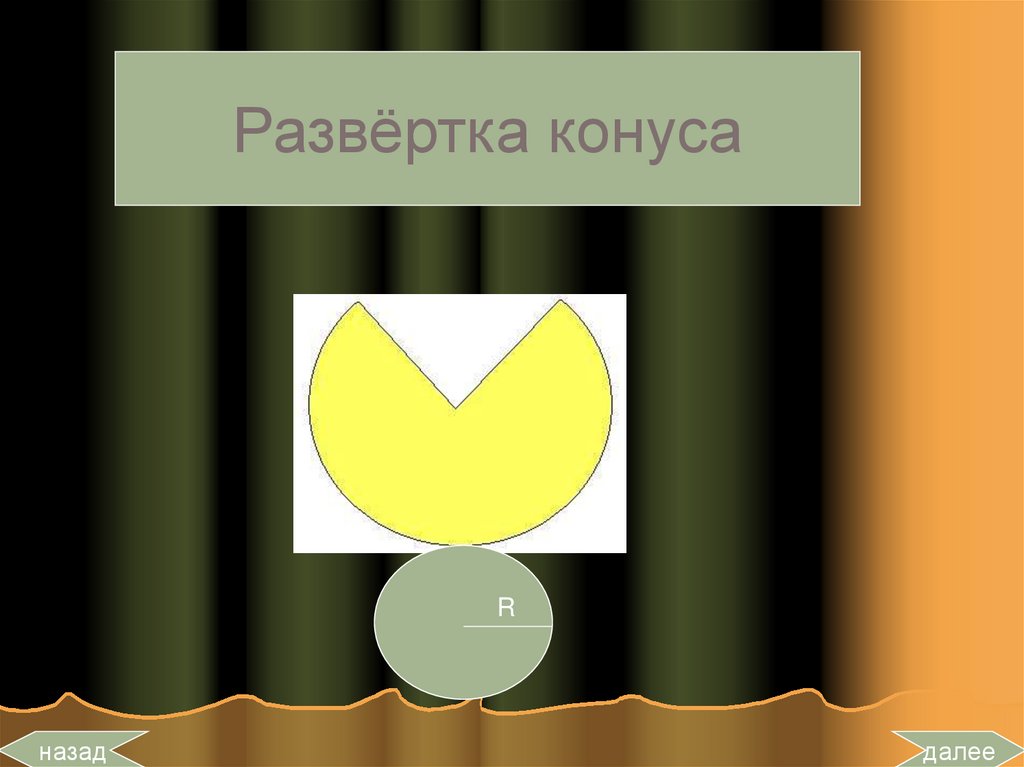
18.
Развёртка конусаL
L
R
назад
далее
19.
ФормулыПлощадь боковой
поверхности
S=ПRL
Площадь полной
поверхности
S=ПR(L+R)
Объём
конуса
назад
V=1/3(ПR2H)
На начало
20. Усеченный конус
Часть конуса,ограниченная его
основанием и
сечением,
параллельным
плоскости
основания,
называется
усеченным
конусом.
21. Усеченный прямой конус
Формулы:1
V h( R 2 RR1 R12 )
3
S бок.пов. ( R R1 )l
S полн.пов. ( R R1 )l R 2 r 2
Здесь h – высота
усеченного конуса; R и
R1 – радиусы его
верхнего и нижнего
оснований; l – его
образующая
На начало
22.
ШарОпределение
Тело, состоящее из всех точек пространства,
находящихся на расстоянии, не большем данного,
от данной точки.
Способ образования
Вращением полукруга или круга вокруг его
диаметра как оси.
На начало
далее
23. Сфера
Определение.Поверхность, состоящая из всех точек
пространства, расположенных на
данном расстоянии от данной точки,
называется сферой.
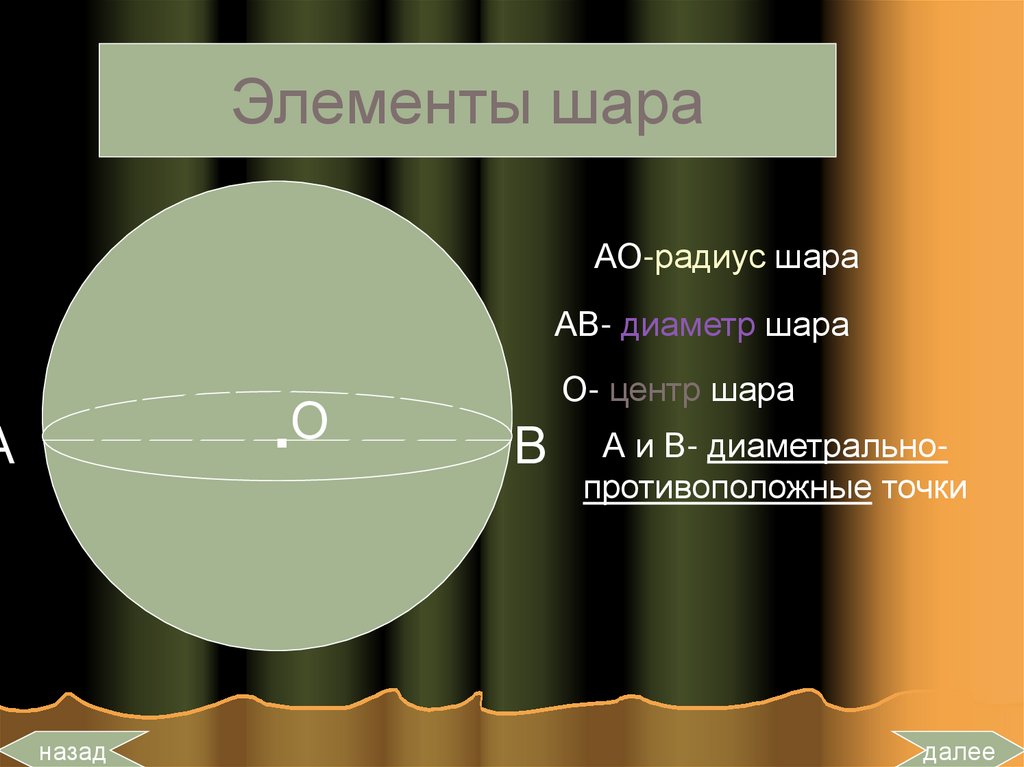
24.
Элементы шараАО-радиус шара
АВ- диаметр шара
.О
А
назад
О- центр шара
В
А и В- диаметральнопротивоположные точки
далее
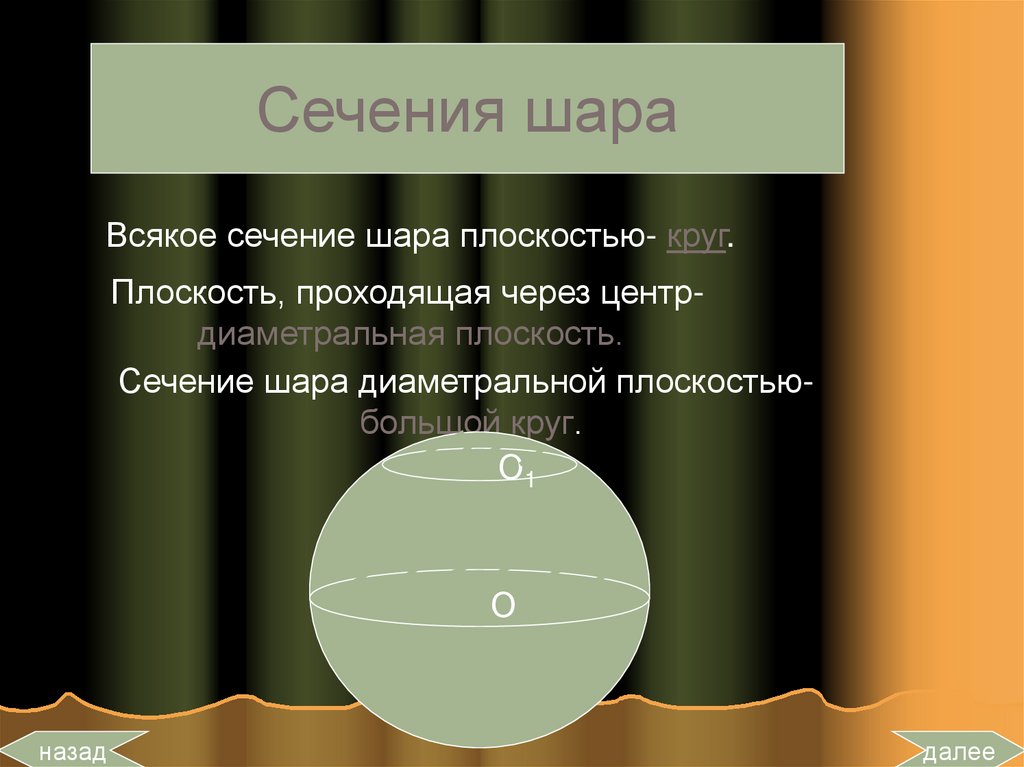
25.
Сечения шараВсякое сечение шара плоскостью- круг.
Плоскость, проходящая через центрдиаметральная плоскость.
Сечение шара диаметральной плоскостьюбольшой круг.
О1
О
назад
далее
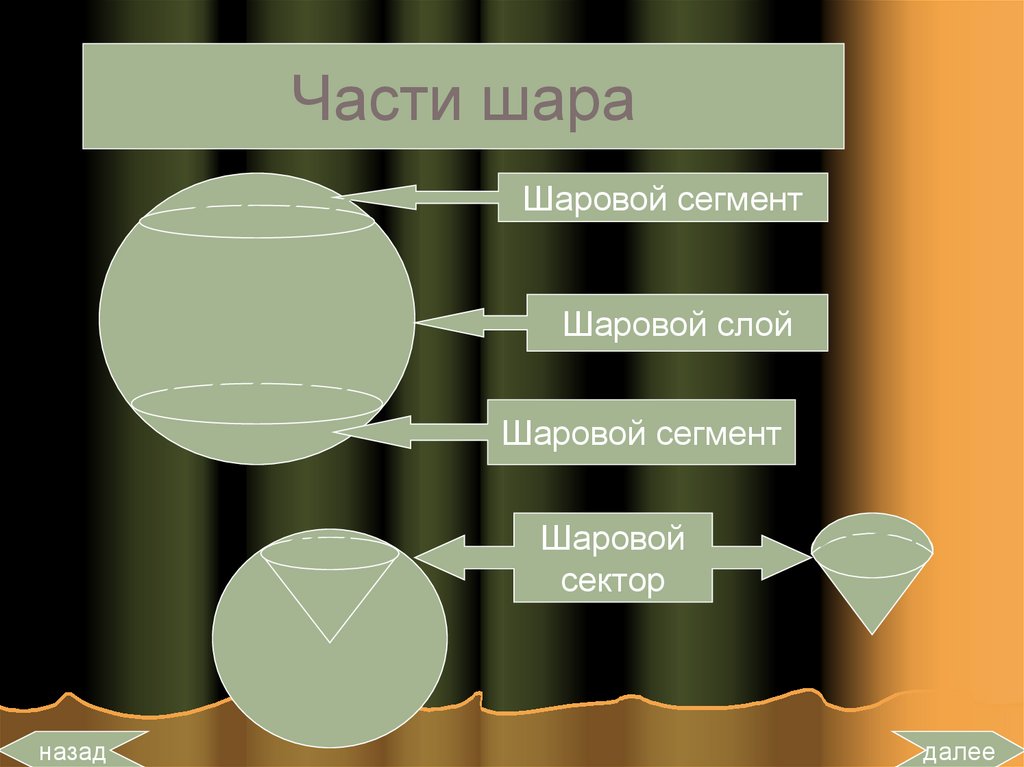
26.
Части шараШаровой сегмент
Шаровой слой
Шаровой сегмент
Шаровой
сектор
назад
далее
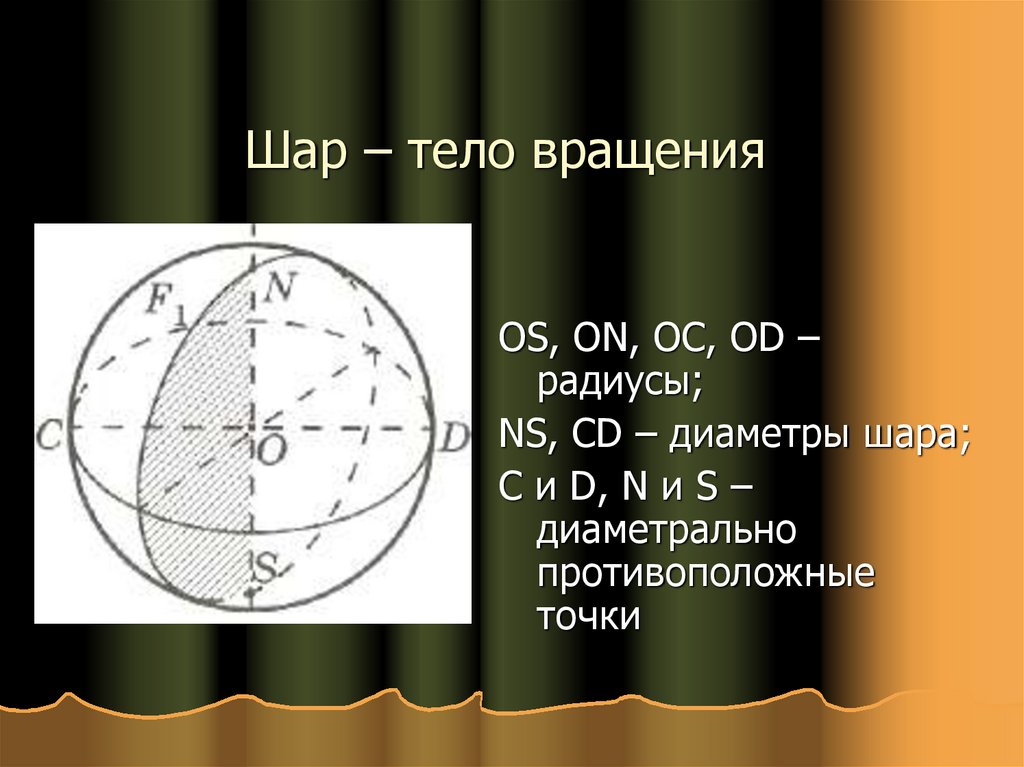
27. Шар – тело вращения
OS, ON, OC, OD –радиусы;
NS, CD – диаметры шара;
C и D, N и S –
диаметрально
противоположные
точки
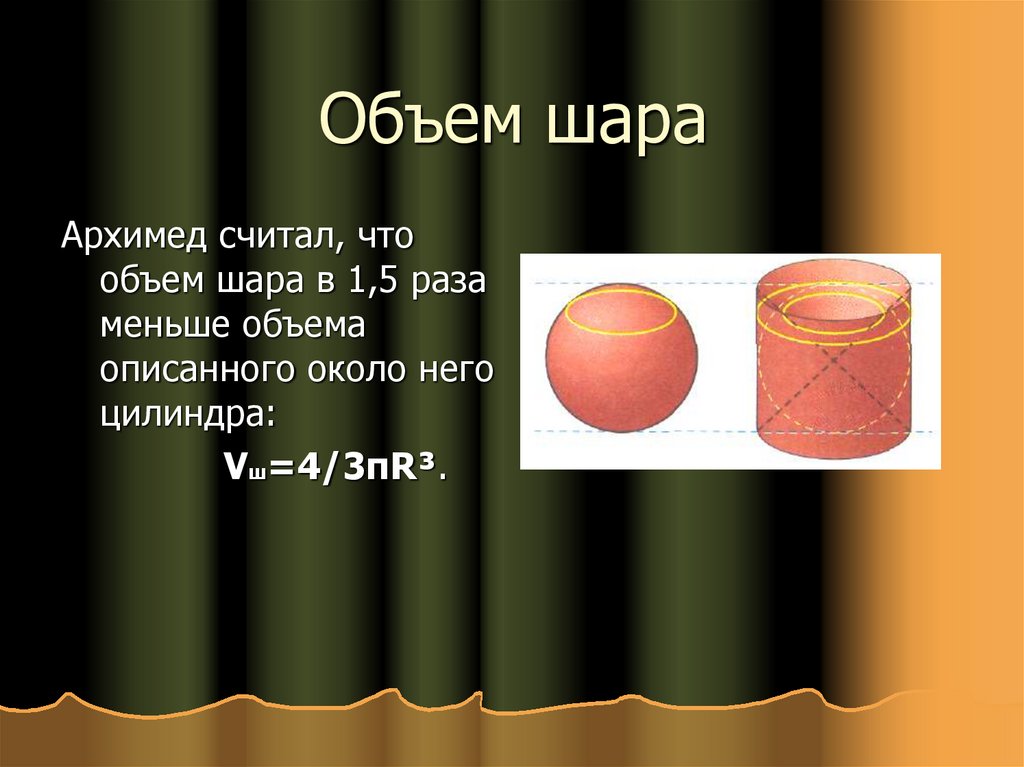
28. Объем шара
Архимед считал, чтообъем шара в 1,5 раза
меньше объема
описанного около него
цилиндра:
Vш=4/3πR³.
29. Как Архимед находил объем шара
Площади сечений:Sц, Sш, Sк.
x Sц 2 R ( S ш S к )
Sц=4πR²;
Sш=π[CE]², где
[CE]²=[EO]²[OC]²=R²-(x-R)²=2Rx-x²;
Sк=π[CD]²= πx²
30.
формулыназад
Площадь сферы
S=4ПR2
Объём шара
V=4/3 (ПR3)
Объём шарового сегмента
V=ПH2(R-H/3)
Объём шарового сектора
V=2/3 (ПR2H)
На начало
вопросы























 Математика
Математика








