Похожие презентации:
Тела вращения
1. Презентация по геометрии на тему: тела вращения
2. Содержание презентации:
ЦилиндрКонус и усечённый конус
Шар и сфера
3. Цилиндр
Определение.Тело, которое образуется при
вращении прямоугольника вокруг
прямой, содержащей его сторону,
называется цилиндром.
4. Круговой прямой цилиндр
5. Наклонный цилиндр
– цилиндр,образующие
которого не
перпендикулярны
плоскостям его
оснований.
6.
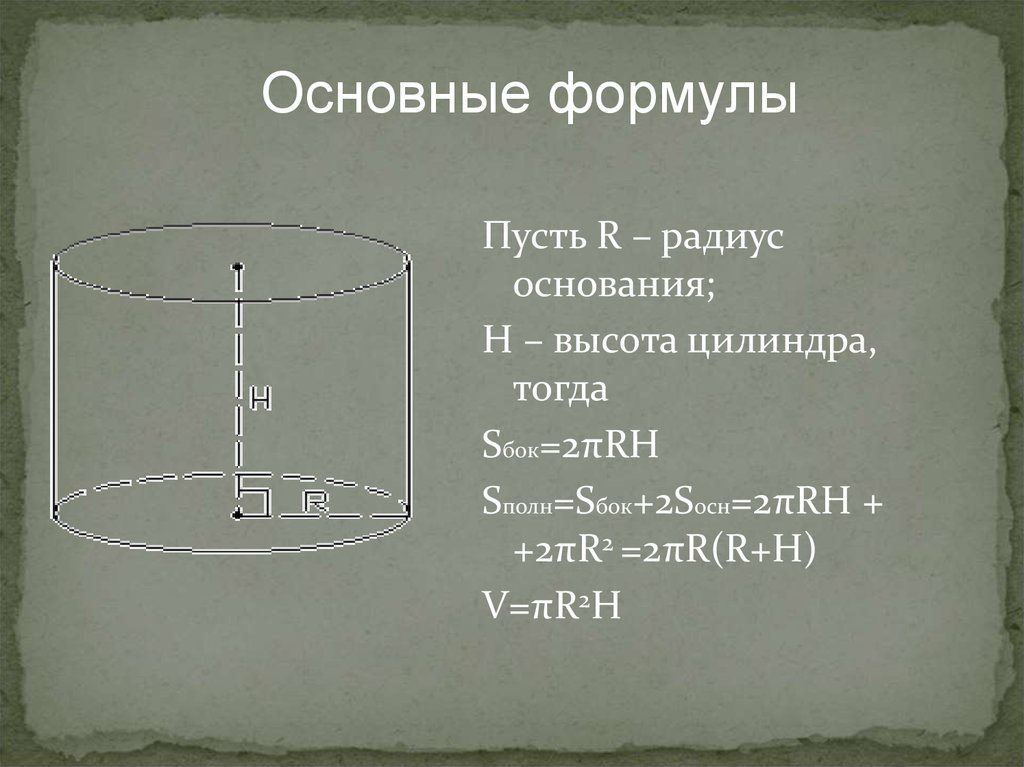
Основные формулыПусть R – радиус
основания;
H – высота цилиндра,
тогда
Sбок=2πRH
Sполн=Sбок+2Sосн=2πRH +
+2πR2 =2πR(R+H)
V=πR2H
7. Конус
Определение.Тело, которое образуется при вращении
прямоугольного треугольника вокруг прямой,
содержащий его катет, называется прямым
круговым конусом.
8. Прямой круговой конус
9.
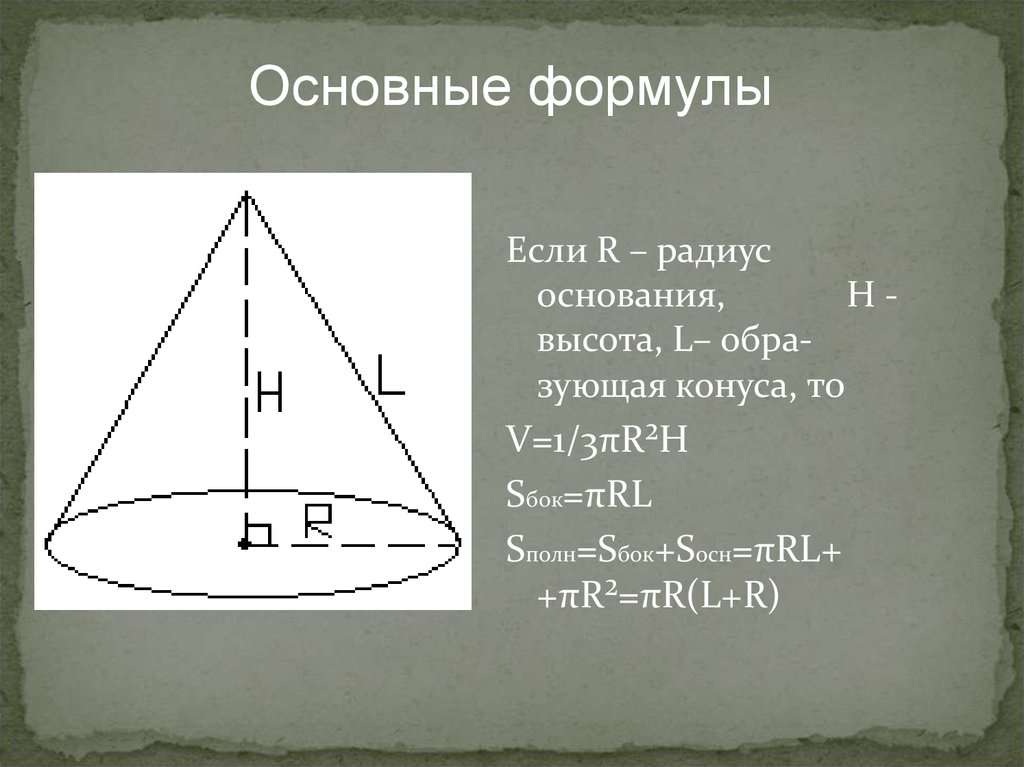
Основные формулыЕсли R – радиус
основания,
Hвысота, L– образующая конуса, то
V=1/3πR²H
Sбок=πRL
Sполн=Sбок+Sосн=πRL+
+πR²=πR(L+R)
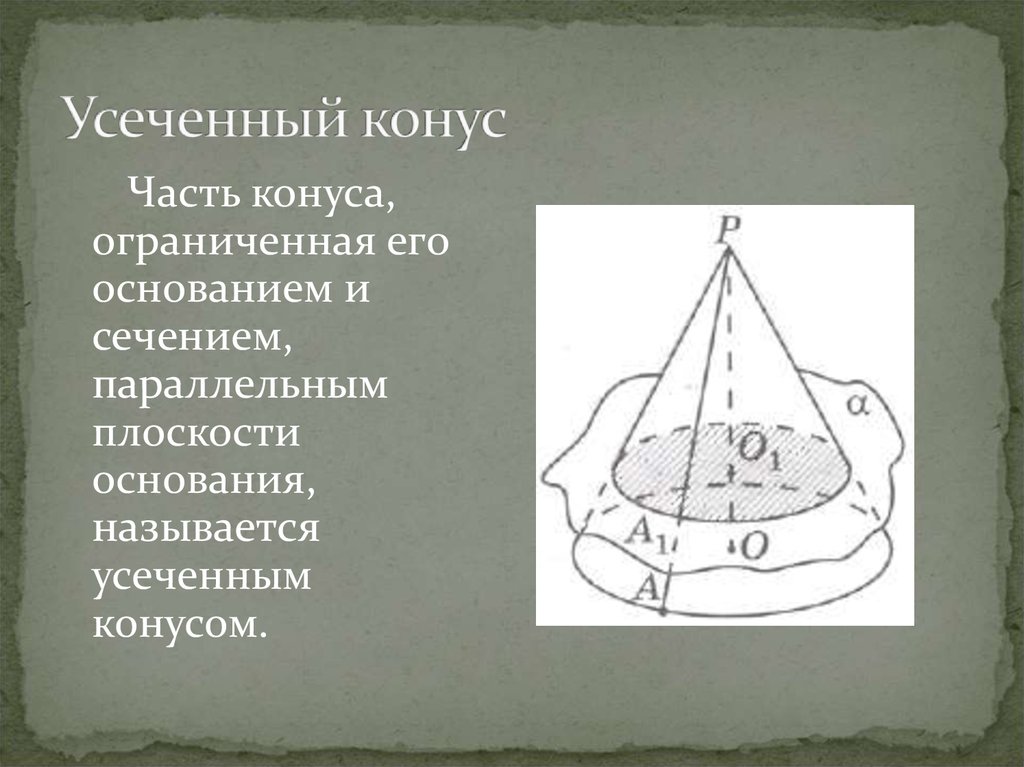
10. Усеченный конус
Часть конуса,ограниченная его
основанием и
сечением,
параллельным
плоскости
основания,
называется
усеченным
конусом.
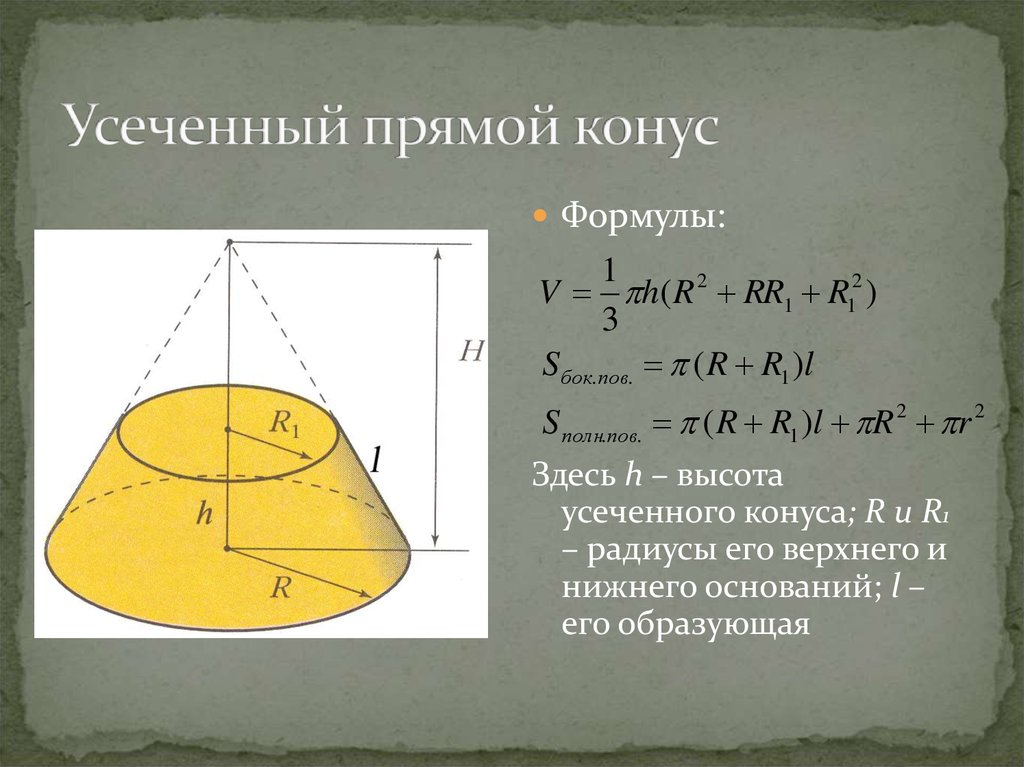
11. Усеченный прямой конус
Формулы:1
V h( R 2 RR1 R12 )
3
S бок.пов. ( R R1 )l
S полн.пов. ( R R1 )l R 2 r 2
Здесь h – высота
усеченного конуса; R и R1
– радиусы его верхнего и
нижнего оснований; l –
его образующая
12. Шар и сфера
Определение.Фигура, полученная в результате вращения
полукруга вокруг диаметра, называется шаром.
Поверхность, образуемая при этом
полуокружностью, называется сферой.
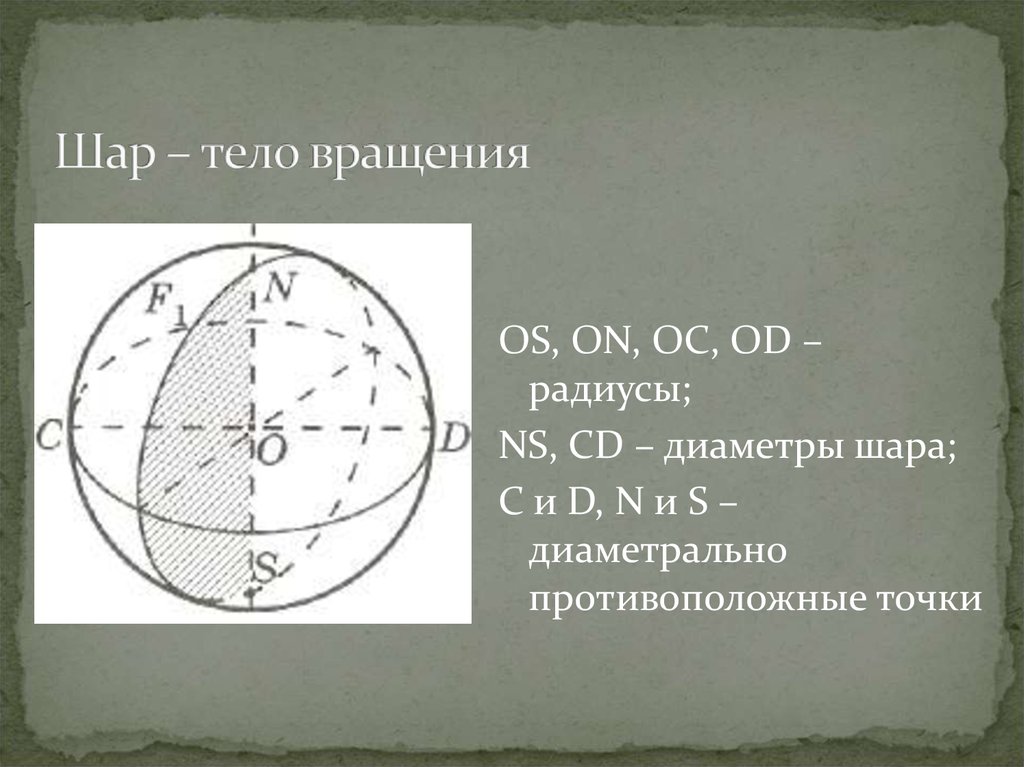
13. Шар – тело вращения
OS, ON, OC, OD –радиусы;
NS, CD – диаметры шара;
C и D, N и S –
диаметрально
противоположные точки
14. Объем шара
Архимед считал, чтообъем шара в 1,5 раза
меньше объема
описанного около него
цилиндра:
Vш=4/3πR³.
15. Как Архимед находил объем шара
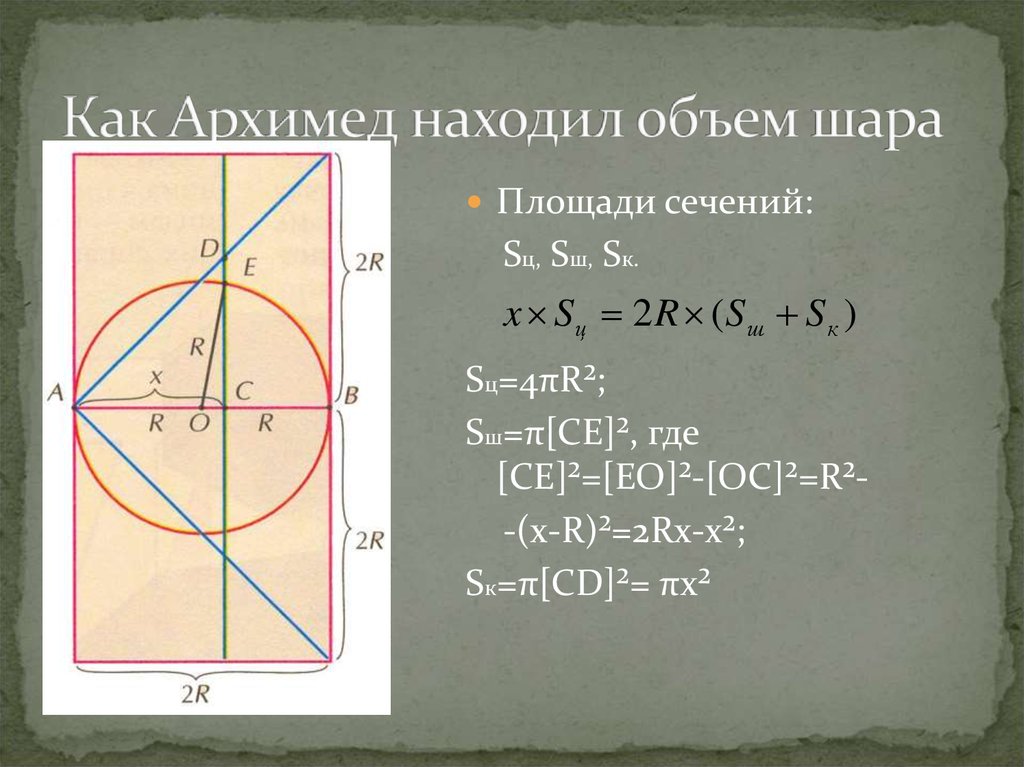
Площади сечений:Sц, Sш, Sк.
x Sц 2 R ( S ш S к )
Sц=4πR²;
Sш=π[CE]², где
[CE]²=[EO]²-[OC]²=R²-(x-R)²=2Rx-x²;
Sк=π[CD]²= πx²
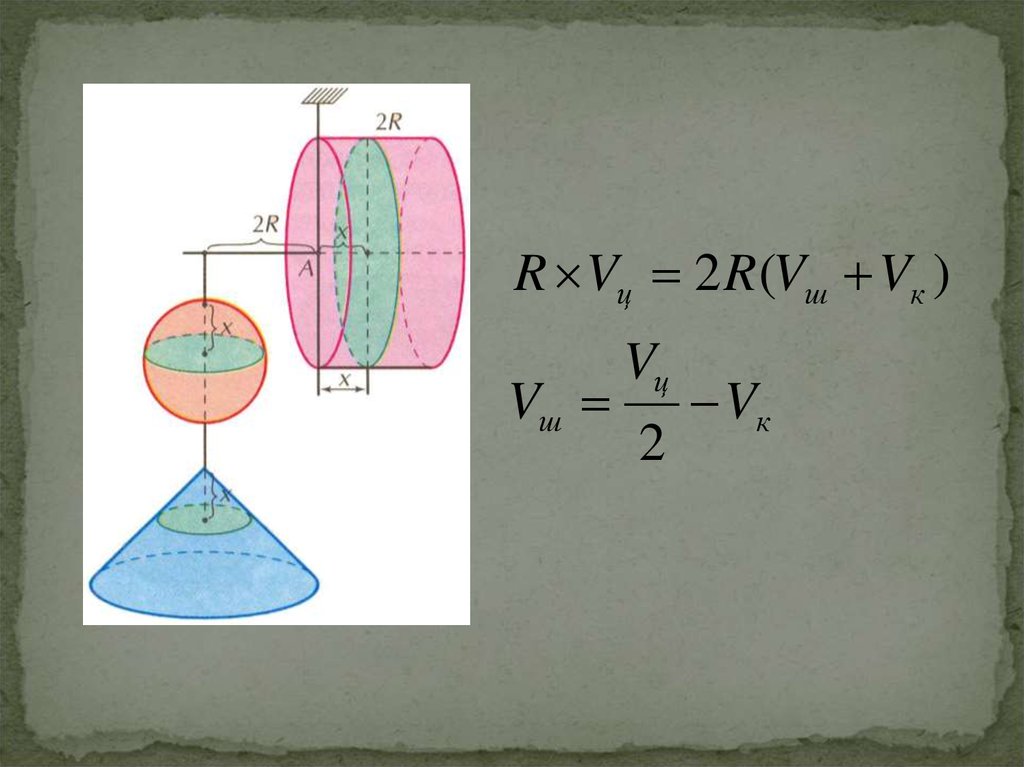
16.
R Vц 2 R (Vш Vк )Vш
Vц
2
Vк
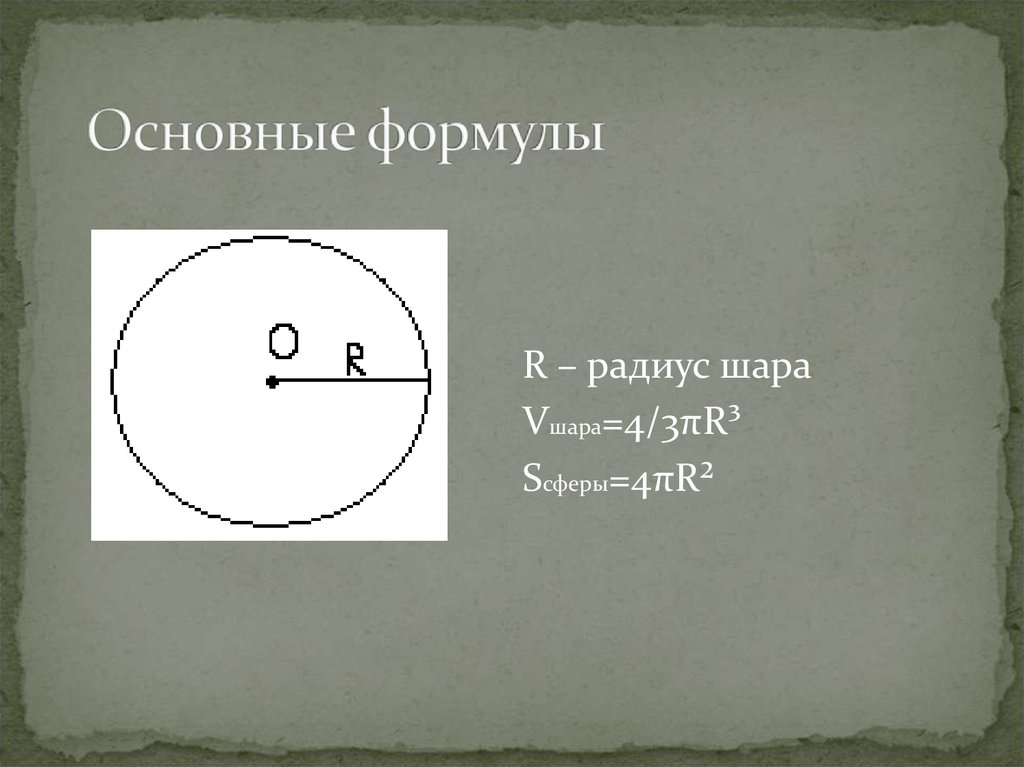
17. Основные формулы
R – радиус шараVшара=4/3πR³
Sсферы=4πR²
18. Уравнение сферы
Пусть A – центр(a; b; c)MA – радиус, тогда
MA²=(x-a)²+(y-b)²+(z-c)²;
(x-a)²+(y-b)²+(z-c)²=R²
19. Тор – фигура вращения
Тор образуется привращении окружности
вокруг не пересекающей её
прямой, лежащей в
плоскости окружности.
Если «заполнить» тор, то
получится тело вращения,
называемое полноторием.
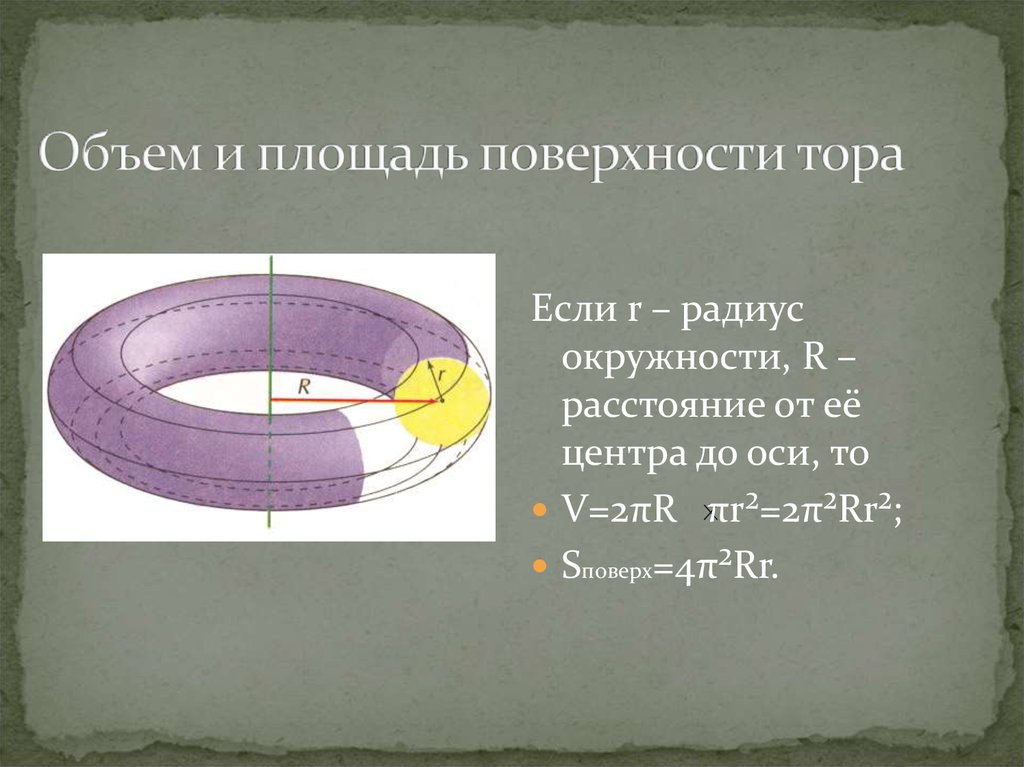
20. Объем и площадь поверхности тора
Если r – радиусокружности, R –
расстояние от её
центра до оси, то
V=2πR πr²=2π²Rr²;
Sповерх=4π²Rr.
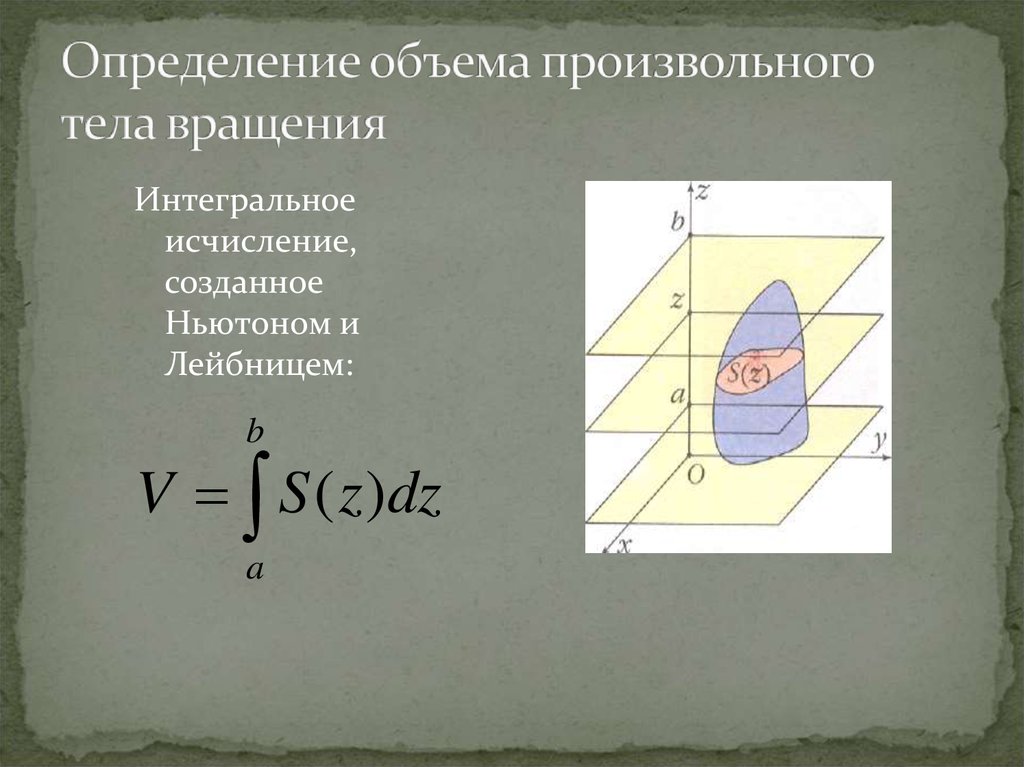
21. Определение объема произвольного тела вращения
Интегральноеисчисление,
созданное
Ньютоном и
Лейбницем:
b
V S ( z )dz
a











 Математика
Математика








