Похожие презентации:
Способы решения систем линейных уравнений
1. Способы решения систем линейных уравнений.
Практическое занятие.2.
Способы решения:а 11 х а 12 у b1
a x a y b
22
2
21
Решить систему уравнений, значит найти пару чисел (Х,У),
являющихся решением каждого из уравнений входящих в систему.
1) Графический способ.
Алгоритм решения:
1) построить в одной системе координат графики функций,
образующих систему;
2) определить точку их пересечения.
3) записать в ответ х= у= .
3.
Решить системы:3
х
у
1
1.
х у 3
2
х
у
6
2.
2 х у 1
4.
Решение:3х у 1
1.
х у 3
3х 1 у
у 3 х
у 3х 1
у 3 х
х 1 2
у 2 5
х 0 3
у 3 0
5.
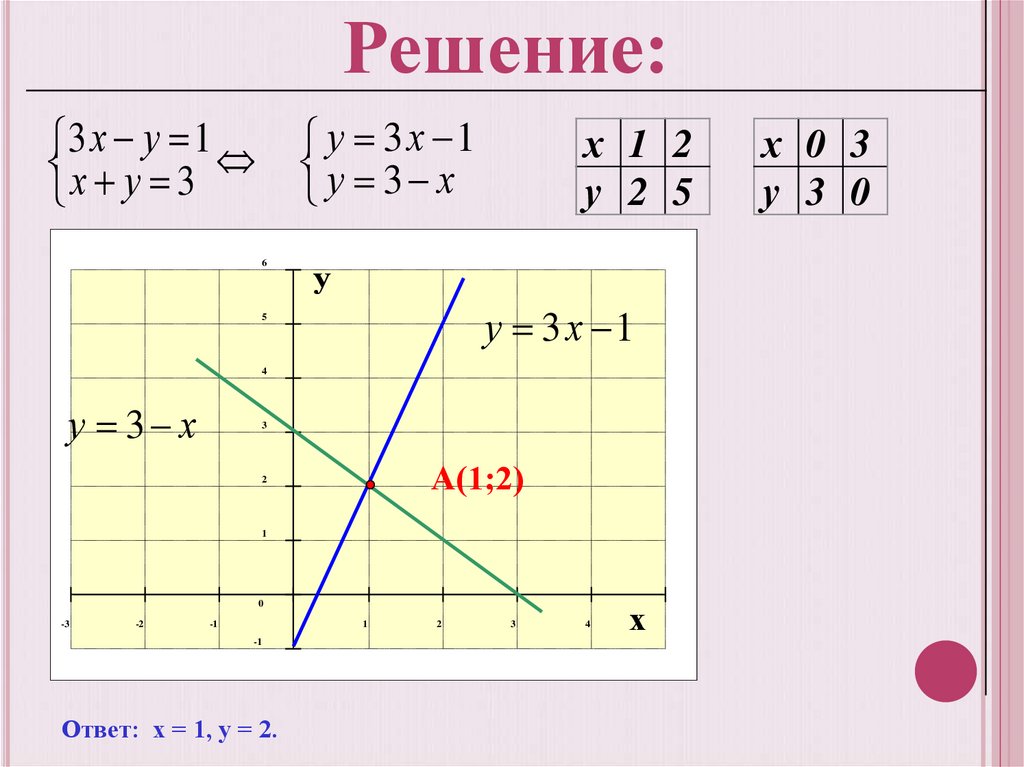
Решение:у 3 х 1
у 3 х
3 х у 1
х у 3
6
х 1 2
у 2 5
у
у 3 х 1
5
4
у 3 х
3
А(1;2)
2
1
0
-3
-2
-1
1
-1
Ответ: х = 1, у = 2.
2
3
4
х
х 0 3
у 3 0
6.
Решение:2
х
у
6
2.
2 х у 1
х 0 1
у 6 4
х 0 -1
у 1 3
у
6
2
х
у 1 2 х
7.
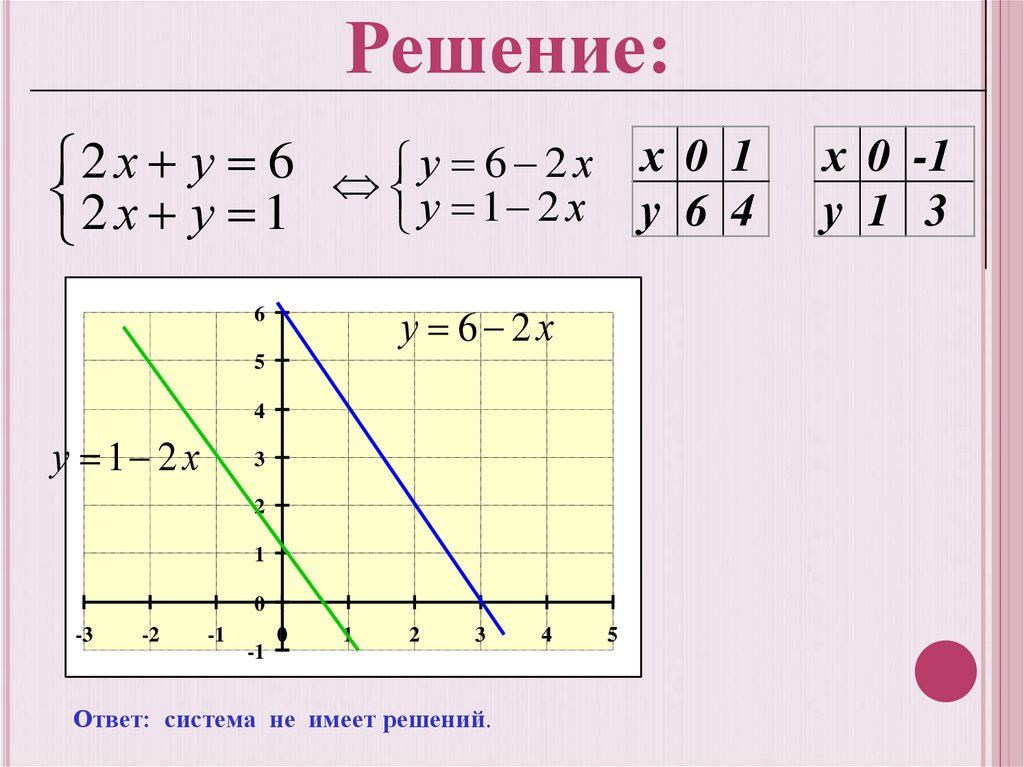
Решение:2 х у 6 у 6 2 х х 0 1
2 х у 1
у
1
2
х
у 6 4
у 6 2х
6
5
4
у 1 2 х
3
2
1
0
-3
-2
-1
-1
0
1
2
3
Ответ: система не имеет решений.
4
5
х 0 -1
у 1 3
8.
Способы решения:2) Способ подстановки.
Алгоритм решения:
1) выразить Х ( или У) из одного уравнения системы;
2) подставить найденное выражение в другое уравнение системы.
5 х 2 у 7 5 х 2 у 7
2 х у 1
у
1
2
х
5 х 2 (1 2 х ) 7 5 х 2 4 х 7
у 1 2х
у 1 2х
х 9 : 9
х 1
х 1
9 х 7 2
у 1 2х у 1 2 1
у 1
у 1 2х
Ответ: х = 1, у = -1.
9.
Определитель:Определителем (детерминантом) второго порядка
называется число, определяемое равенством:
a 11 a 12
det Δ
а 11 а 22 а 12 а 21
a 21 a 22
где
а i j элемент определите ля,
i- номер строки,
j номер столбца .
Пример. Вычислить определитель:
1) 3 4
2 12
3) 0
7
2 ) 10
2
4 ) 1
20
3,
8
5
1
6
3
10.
Определитель:a 11 a 12
det Δ
а 11 а 22 а 12 а 21
a 21 a 22
Пример. Вычислить определитель:
1)
2)
3)
4)
3
4
2
12
10
3
2
8
0
5
7
1
3 12 4 2 36 8 44,
10 8 3 2 80 6 74,
0 1 5 7 0 35 35,
1
6
20
3
1 ( 3) ( 6) 20 3 120 123.
11.
Способы решения:4) Способ определителей.
Алгоритм решения:
1) вычислить три определителя:
Δ
а 11 х а 12 у b1
a x a y b
22
2
21
a 11 a 12
b a
a b
, Δ х 1 12 , Δ у 11 1 .
a 21 a 22
b 2 a 22
a 21 b 2
2) найти Х и У по формулам Крамера:
Δх
х
,
а) если Δ≠0, то система имеет единственное решение,
б) если Δ=0, Δх=0 и Δу=0, то система имеет
бесконечное множество решений,
в) если Δ=0 и хотя бы один из Δх≠0 или Δу≠0,
то система не имеет решений.
у
Δу
12.
Способ определителей:Пример. Решить систему уравнений:
2 х у 3
4 х 8 у 1
13.
Решение:Пример. Решить систему уравнений:
2 х у 3
4 х 8 у 1
2
1
4 8
14.
Решение:Пример. Решить систему уравнений:
2 х у 3
4 х 8 у 1
2
1
4
8
2 8 1 4 16 4 20
3
1
х
3 8 1 1 24 1 23,
1 8
2
3
у
2 1 3 4 2 12 14,
4 1
15.
Решение:Пример. Решить систему уравнений:
2 х у 3
4 х 8 у 1
1 2 8 1 4 16 4 20 0 , значит
2
4 8
имеет единственное решение .
1 3 8 1 1 24 1 23 ,
х 3
1 8
3 2 1 3 4 2 12 14 ,
у 2
4 1
у 14 7
х 23
3
х
1 1,15 ; у
0 , 7.
20
20
20 10
Ответ: х = 1,15; у = 0,7.
система
16.
Задание:Решить системы уравнений:
4 х у 2
1).
10 х 5 у 1
2 х 3 у 6
2).
х у 40
9 х 2 у 3
3).
7 у х 5
11
Ответ : х
;
30
Ответ : х 126 ;
11
Ответ : х
;
65
8
у
15
у 86
48
у
65
17. Спасибо за внимание
СПАСИБО ЗАВНИМАНИЕ















 Математика
Математика








