8_prakt_reshenie_sistem_metodom_Kramera

1.

Решение систем линейных
алгебраических уравнений (СЛАУ)
методом Крамера

2.

Презентация к интегрированному уроку
по теме«Решение систем линейных
уравнений»
Выполнили:
О.Б. Романько,
преподаватель математики ГБПОУ СПбТК;
Е.Ф. Бушманова,
преподаватель математики и информатики
ГБПОУ СПбТК
Санкт-Петербург
2015

3. Определитель матрицы второго порядка

Определителем матрицы второго порядка называют
число, которое вычисляется по формуле:
a11 a12 a11 a12
det
a11a22 a12a21
a21 a22 a21 a22
а11 и а22 образуют главную диагональ матрицы;
а12 и а21образуют побочную диагональ матрицы

4. Вычислите устно

Составьте и вычислите определитель
матрицы системы второго порядка
2 1
y 2x 2
2 ( 5) 3 1 7
3 5
3
x
5
y
5

5. Определитель матрицы третьего порядка

a11 a12 a13
det a21 a22 a23
a31 a32 a33
a11a22a33 a21a32a13 a31a12a23 a31a22a13 a21a12a33 a11a23a32

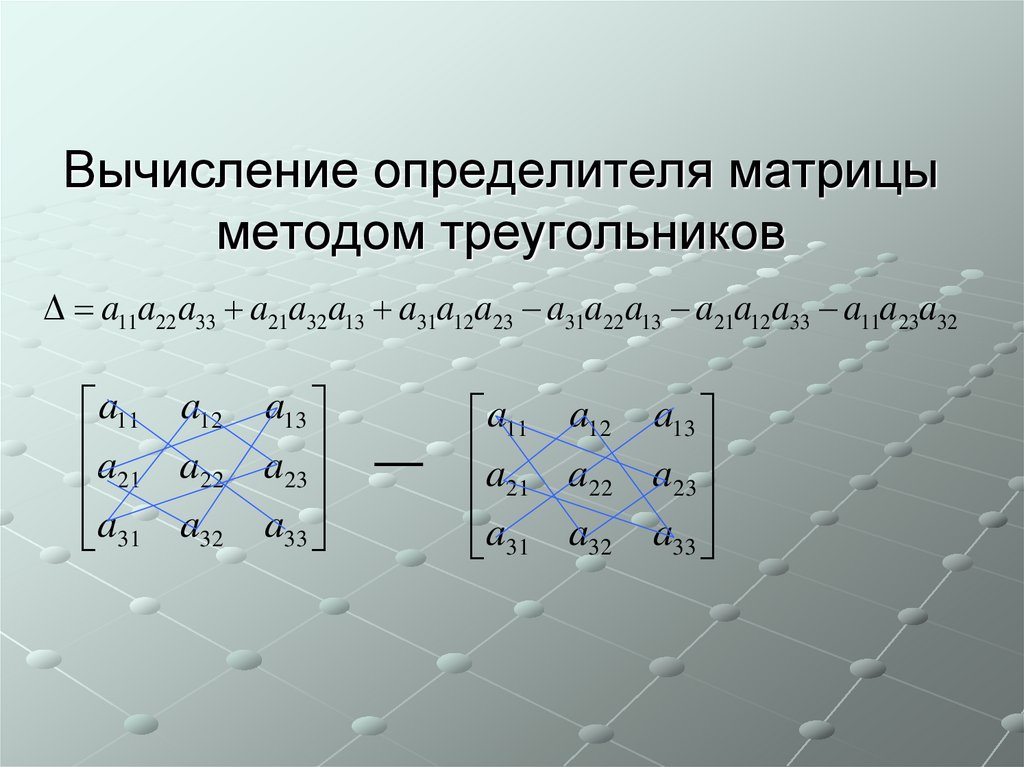
6. Вычисление определителя матрицы методом треугольников

a11a22 a33 a21a32 a13 a31a12a23 a31a22a13 a21a12a33 a11a23a32
a11 a12
a
a
21
22
a31 a32
a13
a23
a33
a11 a12
a
21 a22
a31 a32
a13
a23
a33

7. Вычисление определителя третьего порядка по правилу треугольников

a11 a12 a13
det a21 a22 a23
a31 a32 a33
a11a22 a33 a21a32a13 a31a12 a23 a31a22 a13 a21a12a33 a11a23a32
a11 a12
a
a
21
22
a31 a32
2 1 3
a13
a23
a33
a11 a12
a
21 a22
a31 a32
a13
a23
a33
2 2 1 2∙(-2)∙1 + (-1)∙1∙1+2∙1∙3-3∙(-2)∙1-2 ∙(-1)∙1-1∙1∙2=
1 1 1
=7

8. Вычислите определитель третьего порядка

2 1 3
2 2 1 2∙(-2)∙1 + (-1)∙1∙1+2∙1∙3-3∙(-2)∙1-2 ∙(-1)∙1-1∙1∙2=7
1 1 1

9. Система из m линейных уравнений с n неизвестными имеет вид:

a11 x1 + a12 x2 +... + a1n xn = b1,
a21 x1 + a22 x2 +... + a2n xn = b2,
... ... ...
am1 x1 + am2 x2 +... + amn xn = bm.
...
где аij (i =1..m ; j =1..n ) – заданные
коэффициенты системы
bi – свободные члены системы
xj - неизвестные действительные числа

10. Решение СЛАУ

Решением системы линейных
алгебраических уравнений является
упорядоченный набор значений
переменных, который будучи
подставлен в каждое уравнение, даёт
верные равенства.

11. Способы решения СЛАУ

способ подстановки
способ сложения
графический способ (две переменные)
методом Крамера
методом Гаусса
другие

12. Габриэль Крамер (Gabriel Cramer), швейцарский математик

Дата
рождения:31 июля 1704
Место
рождения:Женева,
Швейцария
Дата
смерти:4 января 1752
(47 лет)
Место смерти:Баньольсюр-Сез,Франция

13.

Крамер одним из первых математиков
пришел к понятию определителя, вывел
формулы решения СЛАУ, доказав
соответствующую теорему в 1750 году
в своей работе «Введение в анализ
кривых линий».

14. Теорема Крамера

• Система линейных алгебраических
уравнений имеет единственное решение
тогда и только тогда, когда определитель
этой системы отличен от нуля.

15. Метод Крамера

Метод широко применяется (как и само
понятие определителя) не только в
высшей алгебре, но и в других разделах
высшей математики, в механике и
теоретической физике.

16. Метод Крамера для систем второго порядка

a11x a12 y b1
a21x a22 y b2
a11
a12
x
a21 a22
b1
a12
b2
a22
y
a11
b1
a21 b2
Если определитель основной матрицы 0, система имеет
единственное решение, которое находится по формулам:
x
x
y
y

17.

• Если Δ=0 и хотя бы один из Δj≠0, то система
несовместна, то есть не имеет решения.
• Если Δ=0 и каждый из Δj=0, то система
имеет бесконечное множество решений.

18. Решите системы методом Крамера

ì
ì 3x + 2y = 5
ì
ì 2x - y = 1
D = -7; D x = -7; D y = -7; x = 1; y = 1
ì
ì 5x + 3y = 12
ì
ì 2x - y = 7
D = -11; D x = -33; D y = 11; x = 3; y = -1
ì
ì 2x + 3y = 12
ì
ì 3x - 2y = 5
D = -13; D x = -39; D y = -26; x = 3; y = 2
Ответы: 1) (1;1) 2) (3;-1) 3) (3;2).

19.

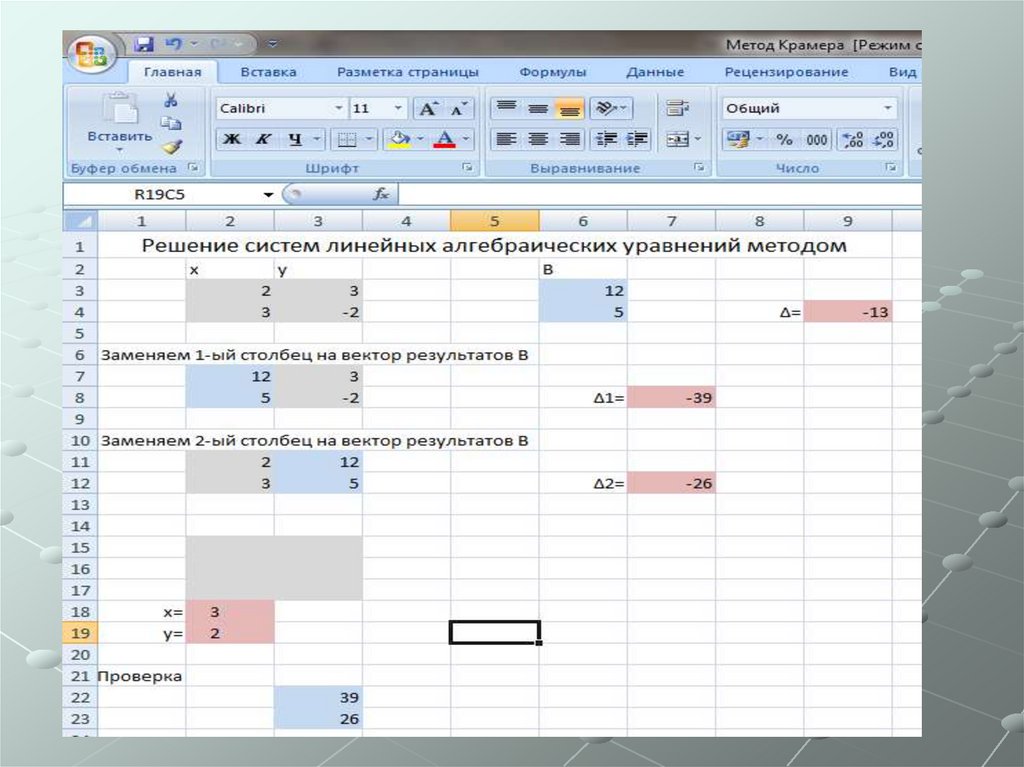
20. Решение системы 3.

2х+3у = 12
3х - 2у = 5
Матрица системы и
столбец свободных
членов
2 3 12
3 2 ; 5
2 3
13 Система имеет единственное решение
3 2
12 3
2 12
1
39 2
26
5 2
3 5
39
26
x
;y
13
13
Ответ: (3;2)

21. Решите систему методом Крамера

у–х=1
2х - 2у = -2
Матрица системы и 1
столбец свободных
2
членов
1 1
det
1 ( 2) 1 2 0
2 2
1 1
;
2 2
Система не может иметь
единственное решение
1
1
1 det
1 ( 2) 1 ( 2) 0
2 2
Система имеет
1 1
бесконечное множество
2 det
(
1
)
(
2
)
1
2
0
решений
2
2

22. Решите системы методом Крамера

y 2x 1
y 2 x 1
6 y 4 x 24
2 x 8 y 10
5 x y 11
3 x 2 y 8

23. Системы трёх линейных уравнений с тремя неизвестными

a11x a12 y a13 z b1
a21x a22 y a23 z b2
a x a y a z b
32
33
3
31
a11 a12 a13
a a a
21 22 23
a31 a32 a33
2 x y 3z 1
2 x 2 y z 1
x y z 0
2 1 3
2 2 1
1 1 1

24.

Пример:
x1 x 2 x3 6
x1 x 2 2 x3 5
2 x x x 1
2
3
1
Уравнение в матричном виде
1 1 1 x1 6
1 1 2 x 5
2
2 1 1 x3 1
Определитель матрицы:
1 1 1
1 2
1 2
1 1
1 1 2 1*
1*
1*
1 5 3 7
1 1
2 1
2 1
2 1 1
Система имеет единственное решение.

25.

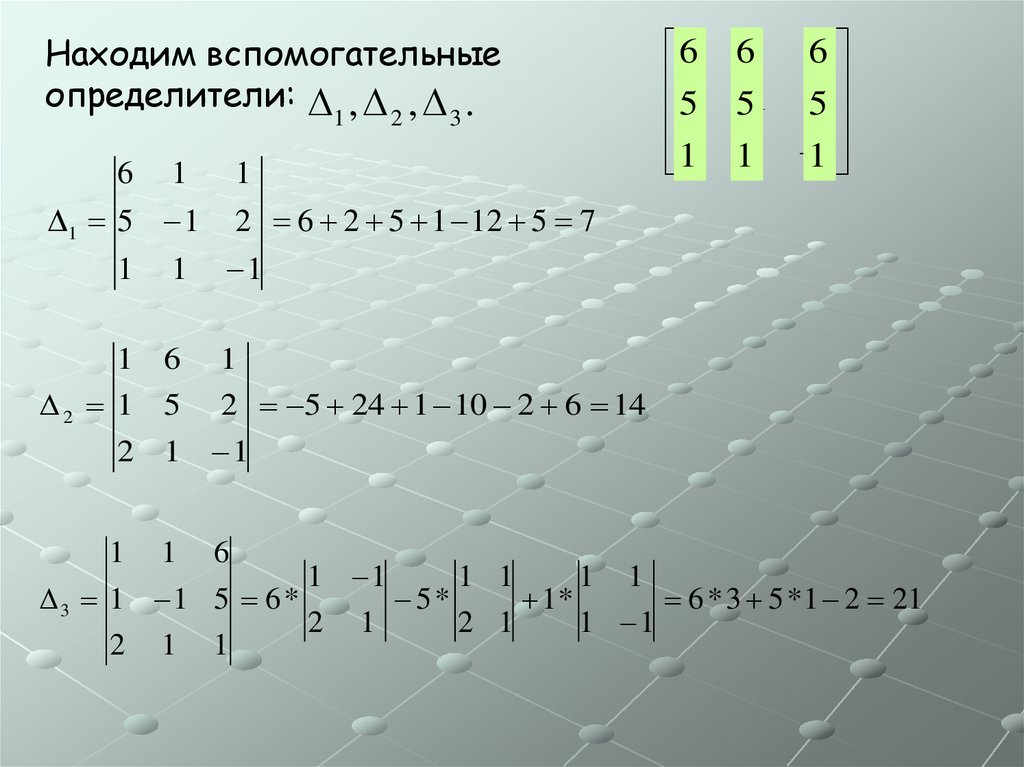
Находим вспомогательные
определители: , , .
1
2
3
6 1 1
1 5 1 2 6 2 5 1 12 5 7
1 1 1
16 61 16
1 1 2
5
5 5
1
2 1 11
1 6 1
2 1 5 2 5 24 1 10 2 6 14
2 1 1
1 1 6
1 1
1 1
1 1
3 1 1 5 6 *
5*
1*
6 * 3 5 *1 2 21
2 1
2 1
1 1
2 1 1

26.

1 7
x1
1
7
2 14
x2
2
7
3 21
x3
3
7
X=(1;2;3)
Проверка:
1+2+3=6 (6=6)
1-2+6=5 (5=5)
2+2-3=1 (1=1)
x1 x 2 x3 6
x1 x 2 2 x3 5
2 x x x 1
2
3
1

27.

28. Решите системы методом Крамера

ì
x + 2y + z = 8
ì
1) ì -2x + 3y - 3z = -5
ì 3x + 4y + 5z = 10
ì
ì 2x - y + 3z = 1
ì
3) ì 2x - 2y + z = 1
ì x+ y+ z= 0
ì
ì
x + 2y + z = 8
ì
2) ì -2x + 3y - 3z = -5
ì 3x - 4y + 5z = 10
ì

29. Ответы: 1)(13;2/3;-19/3) 2)(1;2;3) 3)(1/7;-2/7;1/7)