Похожие презентации:
Решение систем линейных уравнений
1.
1. МЕТОД ГАУССАЭтот
метод
заключается
в
последовательном
исключении
переменных из системы уравнений.
2.
Дана система из трех уравнений:x1 2 x2 3x3 6
2 x1 3x2 x3 4
3x x 4 x 0
3
1 2
Матрица системы будет иметь вид:
1 2 3
2 3 1
3 1 4
Если включить в нее столбец свободных
членов, то она будет называться
расширенной:
3.
1 2 3 6 ( 2)( 3)2 3 1 4
3 1 4 0
Исключим переменную x1
из всех
уравнений,
кроме
первого.
Это
эквивалентно получению нулей во 2-й и
3-ей строке первого столбца.
Для этого умножим первое уравнение на
(-2) и (-3) и сложим соответственно, со 2м и 3-м уравнением:
4.
1 2 3 60 1 7 8 ( 5)
0 5 13 18
Теперь исключим переменную x2
из
третьего уравнения (получим ноль в 3-ей
строке 2-го столбца).
Для этого умножим 2-е уравнение на (-5) и
сложим его с третьим:
1 2
3 6
0 1 7 8
0 0 22 22
5.
Запишемполученную
уравнений:
систему
x1 2 x2 3x3 6
x2 7 x3 8
22 x 22
3
Последовательно находим:
x3 1 x2 7 8 x2 1
x1 2 3 6 x1 1
Ответ:
x1 1
x2 1
x 1
3
6.
2. МЕТОД КРАМЕРАПусть дана система (1). Рассмотрим частный
случай, когда число неизвестных равно
числу уравнений.
Найдем определитель матрицы системы:
A
a11
a12
... a1n
a21
a22 ... a2 n
...
an1
an 2 ... ann
7.
ПустьΔJ –
определитель
матрицы,
полученной из матрицы А заменой j–го
столбца столбцом свободных членов:
1
b1
a12
b2
a22 ... a2 n
a11
... a1n
...
bn an 2 ... ann
2
b1
... a1n
a21 b2 ... a2 n
...
an1 bn
...
... ann
Тогда, если определитель матрицы системы
не равен 0, то система уравнений (1) имеет
единственное
решение,
которое
определяется по формулам:
8.
xjj
( j 1,2...n)
9.
Решим систему из предыдущего примера.Матрица системы имеет вид:
1 2 3
2 3 1
3 1 4
Находим ее определитель:
1 2
2 3
3
1 12 6 6 27 16 1 22
3 1 4
10.
Найдем определители Δ1 , Δ2 , Δ3 :6 2
1 4 3
3
1 72 0 12 0 6 32 22
0 1 4
1 6
2 2 4
3
1 16 18 0 36 48 0 22
3 0 4
1 2 6
3 2 3 4 0 24 12 54 0 4 22
3 1 0
11.
Используем формулы Крамера:22
x1
1
1 22
22
x2
1
2 22
22
x3
1
3 22
Ответ:
x1 1
x2 1
x 1
3
12.
Замечание:Если Δ=0 при том, что хотя бы один
из определителей ΔJ не равен нулю,
то система (1) несовместна.
Если Δ=0 и все ΔJ тоже равны нулю,
то система неопределенная, так как
она имеет бесконечное множество
решений.
13.
3. МЕТОД ОБРАТНОЙ МАТРИЦЫПусть дана система (1). Снова рассмотрим
случай, когда число неизвестных равно
числу уравнений.
В матричной форме система имеет вид:
A X B
Пусть существует обратная матрица А-1 к
матрице системы А.
14.
Тогда решением матричного уравнениябудет матрица-столбец Х:
1
X A B
Проверяем:
1
A A B E B B
15.
Решим систему из предыдущего примера.Матрица системы и столбец свободных
членов имеют вид:
1 2 3
A 2 3 1
3 1 4
6
B 4
0
Найдем обратную матрицу А-1 :
Ранее был найден определитель матрицы А:
A 22
16.
Находим алгебраические дополнения длякаждого элемента матрицы А :
A11 ( 1) M 11
2
A12 ( 1) M 12
3
3 1
1 4
2
3 4
A13 ( 1) M 13
4
A21 ( 1) M 21
3
1
2
12 1 11
( 8 3) 5
2 3
3 1
3
1 4
2 9 7
( 8 3) 11
17.
A22 ( 1) M 224
1
3 4
A23 ( 1) M 23
5
A31 ( 1) M 31
4
(1 6) 5
3 1
3
3 1
1
2 9 11
3
2 1
A33 ( 1) M 33
6
4 9 13
1 2
2
A32 ( 1) M 32
5
3
( 1 6) 7
1
2
2
3
3 4 1
18.
Составляемматрицу
из
найденных
алгебраических дополнений:
11 5 7 T 11 11 11
5 13 7
11 13 5
11 7
7
1
5
1
Транспонируем
ее
и
делим
на
определитель.
Получаем
обратную
матрицу:
11 11 11
1
1
A 5 13 7
22
7
5
1
19.
Находим решение системы уравнений:11 11 11 6
1
1
X A B 5 13 7 4
22
0
7
5
1
( 11) 6 11 4 ( 11) 0
22 1
1
1
5 6 ( 13) 4 7 0 22 1
22
22
1
(
7
)
6
5
4
(
1
)
0
22
Ответ:
x1 1
x2 1
x 1
3
















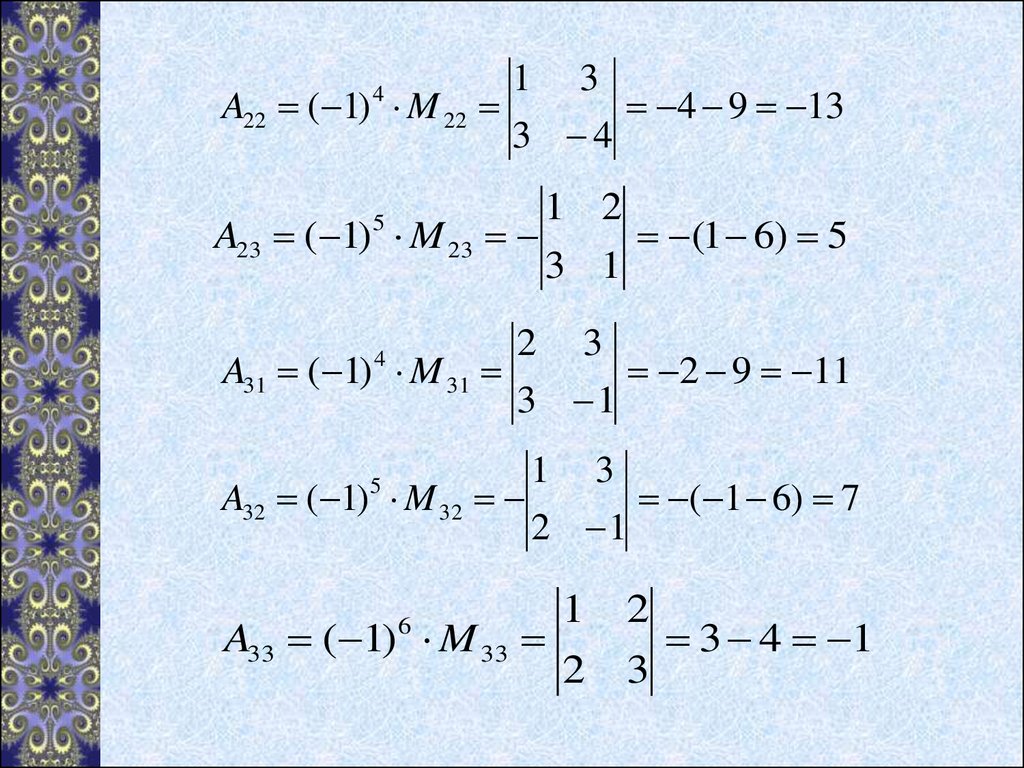


 Математика
Математика








