Статически неопределимые системы. Лекция №5

1. Лекция № 5

10.04.2020г.

2.

Статически неопределимые системы
Статически неопределимыми называются системы, в
которых число реакций связей больше числа основных
уравнений равновесия (уравнений статики).
Плоская система
3 уравнения равновесия
Пространственная
система
6 уравнений равновесия
Если в системе число реакций связей равно числу
основных уравнений равновесия, то она статически
определима.
Если в системе число реакций связей меньше числа
основных уравнений равновесия – это механизм.
В
статически
неопределимых
системах
связи,
накладываемые сверх связей равновесия, называются
дополнительными («лишними»).
Степень статической неопределимости системы равна
числу «лишних» связей.

3.

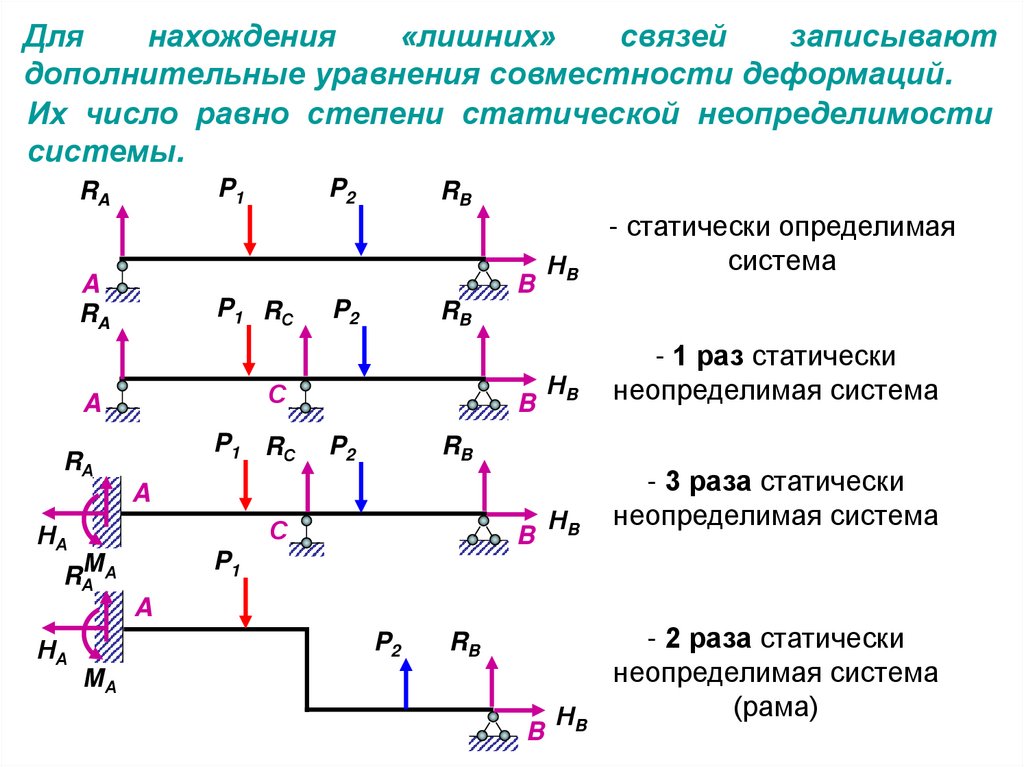
Для
нахождения
«лишних»
связей
записывают
дополнительные уравнения совместности деформаций.
Их число равно степени статической неопределимости
системы.
P1
RA
A
RA
P2
RB
B
P1 RС
P2
P1 RС
RА
B
P2
С
RАМА
НB
- 3 раза статически
неопределимая система
НB
- 2 раза статически
неопределимая система
(рама)
RB
A
НА
НB
- 1 раз статически
неопределимая система
RB
С
A
НB
- статически определимая
система
B
P1
A
НА
P2
RB
МА
B

4.

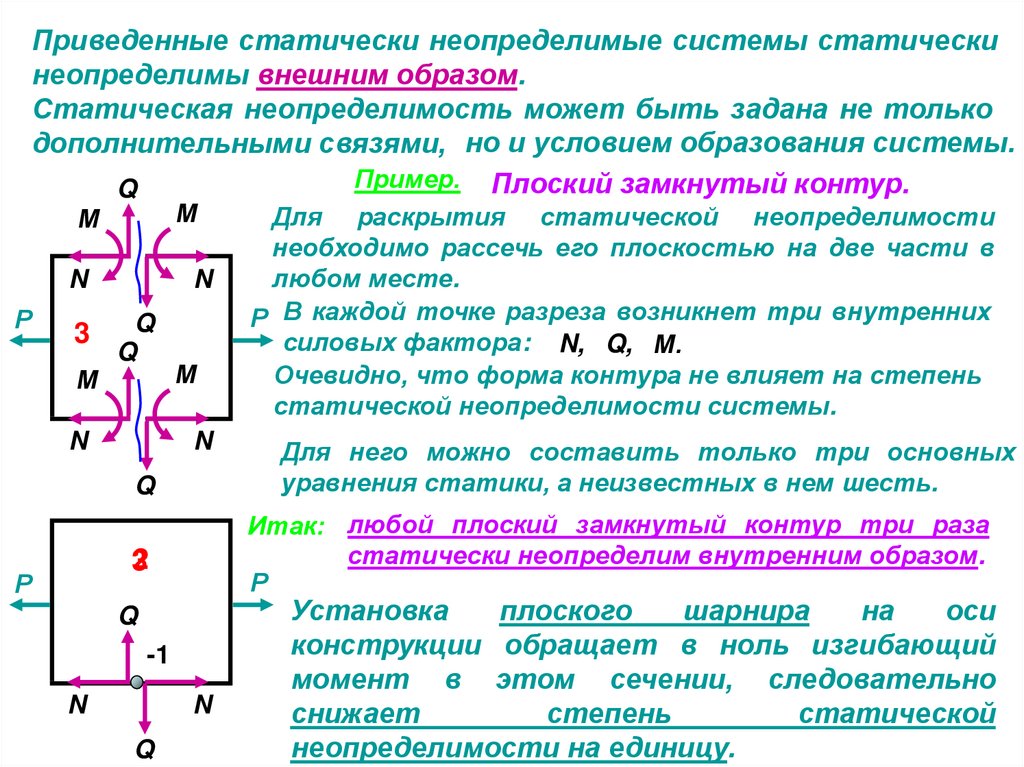
Приведенные статически неопределимые системы статически
неопределимы внешним образом.
Статическая неопределимость может быть задана не только
дополнительными связями, но и условием образования системы.
Пример. Плоский замкнутый контур.
Q
М
М
N
Р
3
М
N
Q
Q
N
М
N
Q
Q
-1
N
N
Q
Для него можно составить только три основных
уравнения статики, а неизвестных в нем шесть.
Итак: любой плоский замкнутый контур три раза
статически неопределим внутренним образом.
Р
2
3
Р
Для раскрытия статической неопределимости
необходимо рассечь его плоскостью на две части в
любом месте.
Р В каждой точке разреза возникнет три внутренних
силовых фактора: N, Q, М.
Очевидно, что форма контура не влияет на степень
статической неопределимости системы.
Установка
плоского
шарнира
на
оси
конструкции обращает в ноль изгибающий
момент в этом сечении, следовательно
снижает
степень
статической
неопределимости на единицу.

5.

Р
Р
3
-2
-2
3
-1
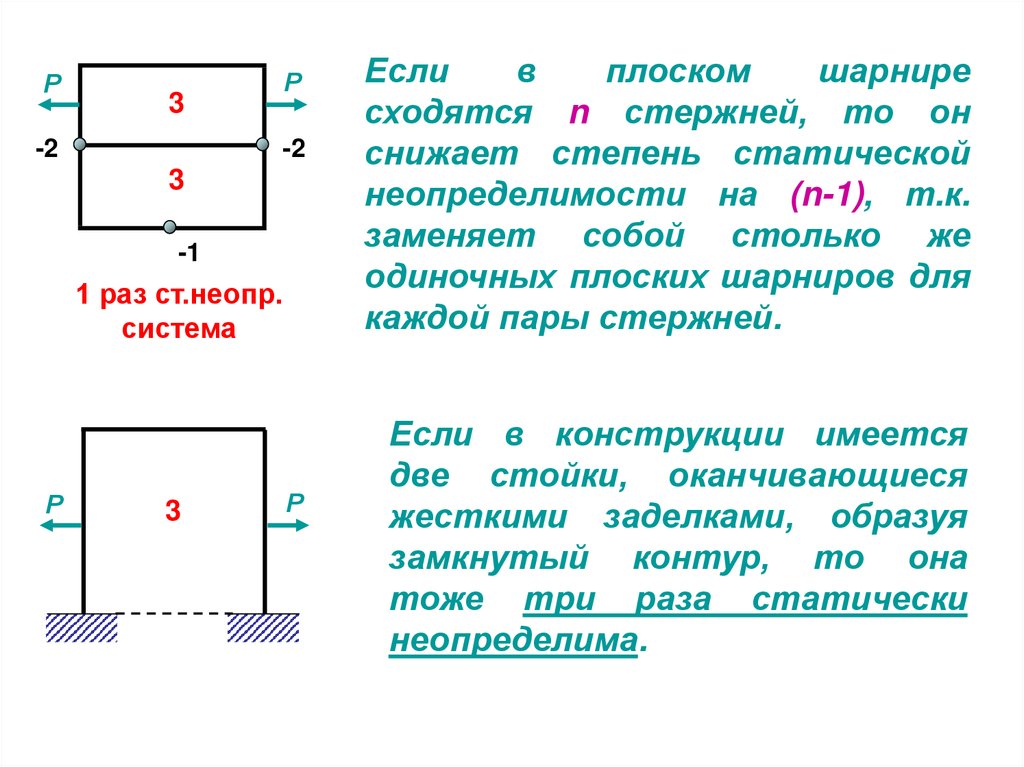
1 раз ст.неопр.
система
Р
3
Р
Если
в
плоском
шарнире
сходятся n стержней, то он
снижает степень статической
неопределимости на (n-1), т.к.
заменяет собой столько же
одиночных плоских шарниров для
каждой пары стержней.
Если в конструкции имеется
две стойки, оканчивающиеся
жесткими заделками, образуя
замкнутый контур, то она
тоже три раза статически
неопределима.

6.

Раскрыть статическую неопределимость означает
найти все неизвестные реакции связей.
Канонические уравнения метода сил.
Применяются
для
раскрытия
неопределимости рам и балок.
P1
RА
Исходная (заданная) система
A
НА
P2
МА
P1
RА
A
НА
P2
МА
статической
RB
Отбросим
дополнительные связи.
Например,
будем
Н
B B
считать опору В
дополнительной
связью.
Основная система - система, освобожденная
от дополнительных связей.

7.

В основной системе перемещения по направлению
отброшенных связей должны быть равны нулю, что
выражается уравнением:
i i 1 i 2 i 3 in 1 in iР 0 (1)
где: i - суммарное перемещение по направлению
i 1
i-той отброшенной связи;
in - перемещения от каждой отброшенной
связи в отдельности;
iР - перемещение от всех внешних нагрузок (грузовое).
ij
Обозначение индексов в перемещениях:
• первый индекс i - обозначает номер отброшенной связи;
• второй индекс j - обозначает номер силового фактора,
вызвавшего перемещение.

8.

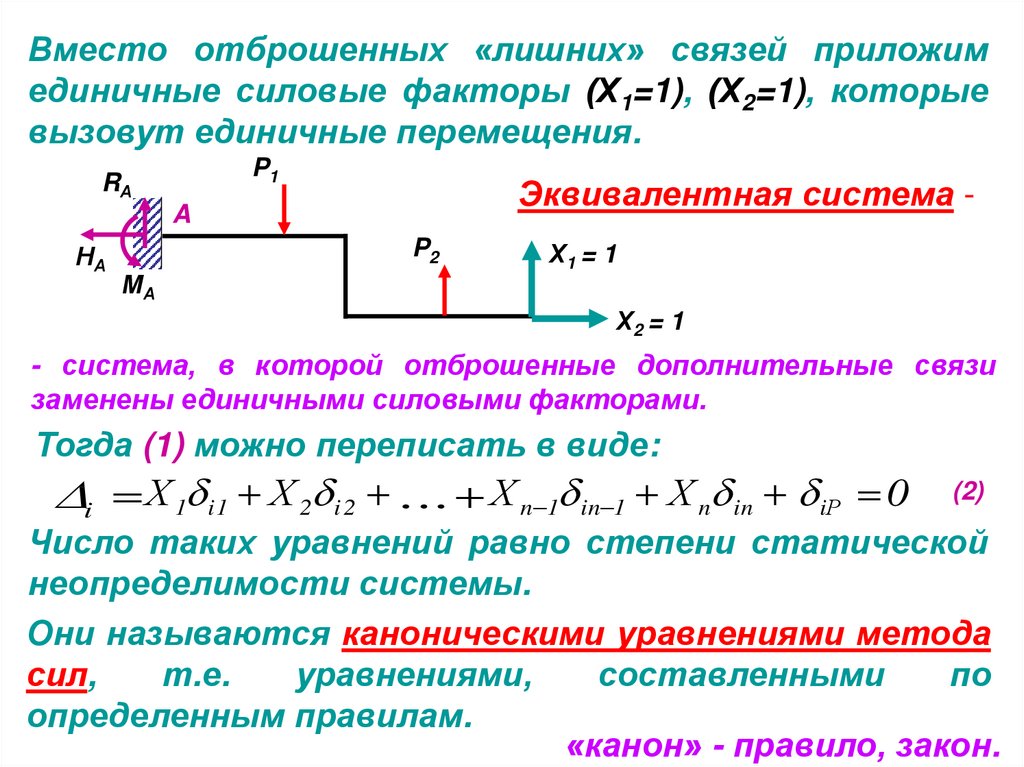
Вместо отброшенных «лишних» связей приложим
единичные силовые факторы (Х1=1), (Х2=1), которые
вызовут единичные перемещения.
P1
RА
Эквивалентная система -
A
НА
P2
МА
Х1 = 1
Х2 = 1
- система, в которой отброшенные дополнительные связи
заменены единичными силовыми факторами.
Тогда (1) можно переписать в виде:
i Х 1 i1 Х 2 i 2 Х n 1 in 1 Х n in iР 0
(2)
Число таких уравнений равно степени статической
неопределимости системы.
Они называются каноническими уравнениями метода
сил,
т.е.
уравнениями,
составленными
по
определенным правилам.
«канон» - правило, закон.

9.

В общем виде для «n» раз статически неопределимой
задачи система канонических уравнений метода сил
выглядит так:
Х 1 11 Х 2 12 Х 3 13 Х n 1n 1Р 0
Х 1 21 Х 2 22 Х 3 23 Х n 2 n 2 Р 0
Х 1 31 Х 2 32 Х 3 33 Х n 3 n 3 Р 0
. . . . . . . . . . . . . . . . . . . . . . . . . . .
Х 1 n1 Х 2 n 2 Х 3 n 3 Х n nn nР 0
Единичные перемещения ij и грузовые перемещения
iР определяются с помощью интеграла Мора или
способа Верещагина.
Для этого выстраивают единичные и грузовые
эпюры моментов: М х 1 , М х 2 , М х 3 , , М хn ; М хР .

10.

ij ji тогда:
12 21 ; 13 31 ; 23 32 ; ;
По теореме Максвелла имеем:
1n n 1 ; 2 n n 2 ; 3 n n 3 .
Решив
систему
канонических
уравнений
относительно неизвестных Х1 , Х2 , … , Хn ,
прикладывают их (с учетом знака) к основной
системе вместо отброшенных дополнительных
связей.
Затем решают основную систему, учитывая
найденные Х1 , Х2 , … , Хn как обычные силовые
факторы.
Проверка
правильности
нахождения
заключается
в
контроле
равенства
перемещений по их направлениям.
связей
нулю

11.

Для расчета одной и той же исходной статически
неопределимой системы можно использовать несколько
вариантов выбора основной системы.
P1
RА
Исходная (заданная)
система
A
НА
P2
RB
МА
B
а)
НB
P1
RА
A
НА
P2
Х1 = 1
МА
Х2 = 1
б)
Х1 = 1
Варианты основных
и эквивалентных
систем
RА
Х2 = 1
НА
P1
А
P2
RА
А
P1
в)
P2
RB
RВ
В
Х2 = 1
B
НB
Х1 = 1

12.

Рационально выбирать такую основную систему, которая дает
наиболее простые единичные и силовые эпюры моментов.
Пример.
RА
A
НА
МА
A
Раскрыть статическую неопределимость однопролетной
балки.
Система один раз статически неопределима:
4 неизвестные реакции связей
P = ql
RВ
- 3 основных уравнения равновесия
В 1 степень статической неопределимости
Запишем одно каноническое уравнение метода
l /2
l /2
сил:
P = ql
X1=1 Эквивалентная система
Основная система
Х 1 11 1Р 0
(МхP)= ql2 ·l /2·2·2
ql2/2
l
C
yc(Mx1)= 5l /6
(Мх1)= l·l /2
C
A
l /2
5ql2/32
6ql2/32
11ql/16
Q
Mx1
yc(Mx1)= 2l /3
P = ql
M
MxP
5ql/16
RВ=5ql/16
l /2
Х1
1Р
11
Определяем единичное δ11 и силовое δ1Р
перемещения
с
помощью
способа
М х 1 у с М х 1 l l 2l
Верещагина:
l3
11
EI x
2 EI x 3 3EI x
2
4
М хР ус М х 1
ql l 5l
5
ql
1Р
EI x
2 2 2 EI x 6
В
48 EI x
5ql 4 3 EI x 5ql
Определяем Х 1
3
16
48 EI x l
5 ql
6 ql 2
Cтроим эпюру M. M A
Итак: RB
32
16
11ql
НА 0
Строим эпюру Q. R А
16

13.

Уравнение трех моментов
(уравнение Клапейрона).
Применяется для раскрытия статической неопределимости
многопролетных неразрезных балок.
Пролет – это расстояние между двумя соседними опорами,
двумя соседними заделками или соседними опорой и заделкой.
В
A
В
A
В
A
Многопролетными называются балки, в которых более одного
пролета.
A
пролет
В
пролет
С
пролет
D
консоль
Многопролетные балки всегда
статически неопределимы.
Исходная система
q
0
P
1
q
2
n-1
P
n
M
n+1
m

14.

Основная система
M1
q
0
M2
P
1
Mn-1
2
n-1
q
Mn
P Mn+1
n+1
n
M
m
В основной системе лишними связями будем считать не
промежуточные опоры и реакции в них, а изгибающие
моменты.
Любая опора или заделка запрещает линейные перемещения.
Но в опорах изгибающий момент отличен от нуля, т.к. опора
допускает угол поворота сечения.
Следовательно,
основной
системой
будет
система
однопролетных балок, соединенных на опорах шарнирами.
Эквивалентной будет система из ряда простых шарнирноопертых
балок,
нагруженных
заданной
нагрузкой
и
неизвестными моментами по концам каждой.
q
0
M1
1
P
Эквивалентная система
M2
Mn-1 q
Mn
2
n-1
n
P Mn+1
n+1
M
m

15.

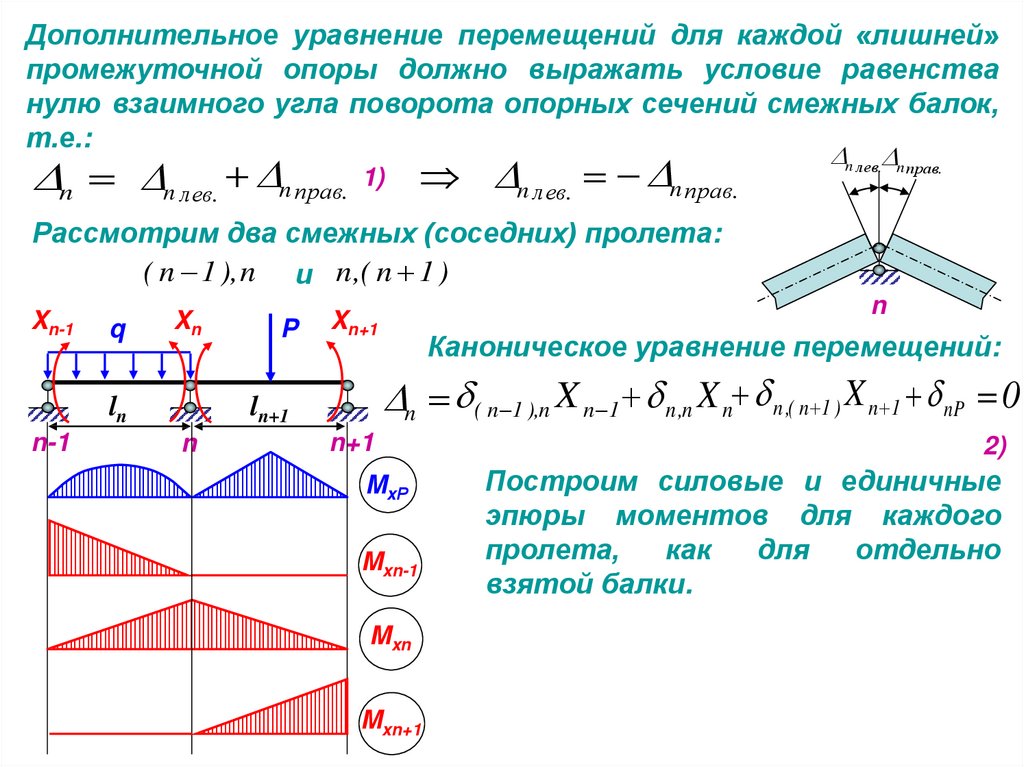
Дополнительное уравнение перемещений для каждой «лишней»
промежуточной опоры должно выражать условие равенства
нулю взаимного угла поворота опорных сечений смежных балок,
т.е.:
n лев. n прав.
n n лев. n прав.
1)
n лев. n прав.
Рассмотрим два смежных (соседних) пролета:
( n 1 ), n и n ,( n 1 )
Xn-1
q
Xn
ln
n-1
P
Каноническое уравнение перемещений:
n ( n 1 ),n X n 1 n ,n X n n ,( n 1 ) X n 1 nP 0
ln+1
n
n
Xn+1
n+1
MxР
Mxn-1
Mxn
Mxn+1
2)
Построим силовые и единичные
эпюры моментов для каждого
пролета,
как
для
отдельно
взятой балки.

16.

Xn-1=1 q
Xn=1
ln
an
n n+1
bn
an+1
n+1
MxР
bn+1
1
Mxn-1
1/3
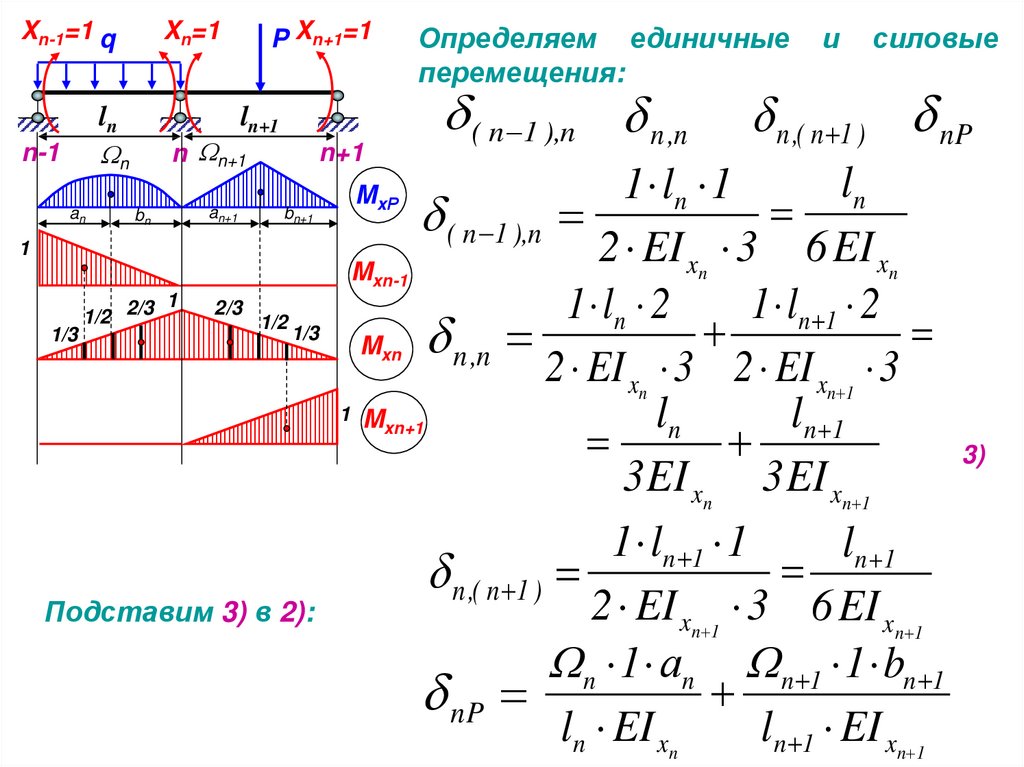
Определяем единичные
перемещения:
( n 1 ),n n ,n
ln+1
n
n-1
P Xn+1=1
1
1/2 2/3
2/3
1/2
1/3
Mxn
1
Подставим 3) в 2):
и
силовые
n ,( n 1 ) nP
ln
1 ln 1
( n 1 ),n
2 EI xn 3 6 EI xn
1 ln 2
1 ln 1 2
n ,n
2 EI xn 3 2 EI xn 1 3
ln 1
ln
3 EI xn 3 EI xn 1
1 ln 1 1
ln 1
n ,( n 1 )
2 EI xn 1 3 6 EI xn 1
n 1 аn n 1 1 bn 1
nP
ln EI xn
ln 1 EI xn 1
Mxn+1
3)

17.

Подставим 3) в 2):
b
а
ln
ln
l
l
n
1
n 1
n
n
n
1
n 1
X n 1
X
0
Xn
n 1
3 EI x 3 EI x
6 EI xn
6 EI xn 1
ln EI xn ln 1 EI xn 1
n
n 1
Упростим выражение, приведя его к общему знаменателю:
ln ln 1
а
b
ln
l
n
n
n
1
n
1
n
1
X n 1
4)
X n 1
2Xn
6
Ix Ix
I xn
I
l
I
l
I
x
n 1
n
n 1
n 1 xn 1
n xn
- уравнение Клапейрона.
(впервые опубликовано в 1857г. во Франции).
Если жесткость участков одинакова и постоянна EI x const ,
при следующих заменах: X n 1 M л ; X n M ср ; X n 1 M пр ;
ln l л ; ln 1 lпр получаем:
nр bnр
л ал
М лl л 2 М ср l л lпр М прlпр 6
0
lnр
lл
i 1
i 1
n
n
- уравнение трех моментов.
5)

18.

л а л n nр bnр
М лl л 2 М ср l л lпр М прlпр 6
0
lnр
lл
i 1
i 1
n
- уравнение трех моментов.
где:
- моменты на левой, средней и правой
опорах двух смежных пролетов;
- длины левого и правого смежных пролетов;
M л ; M ср ; M пр
l л ; l пр
л ; пр-
ал
площади силовых эпюр моментов под левым и
правым пролетами;
- расстояние от центра тяжести площади силовой
эпюры моментов под левым пролетом до левой
границы левого пролета;
bпр -
расстояние от центра тяжести площади силовой
эпюры моментов под правым пролетом до правой
границы правого пролета;
i 1 n - количество силовых эпюр моментов под всеми
пролетами.
Число уравнений трех моментов должно быть равно степени
статической неопределимости многопролетной балки.

19.

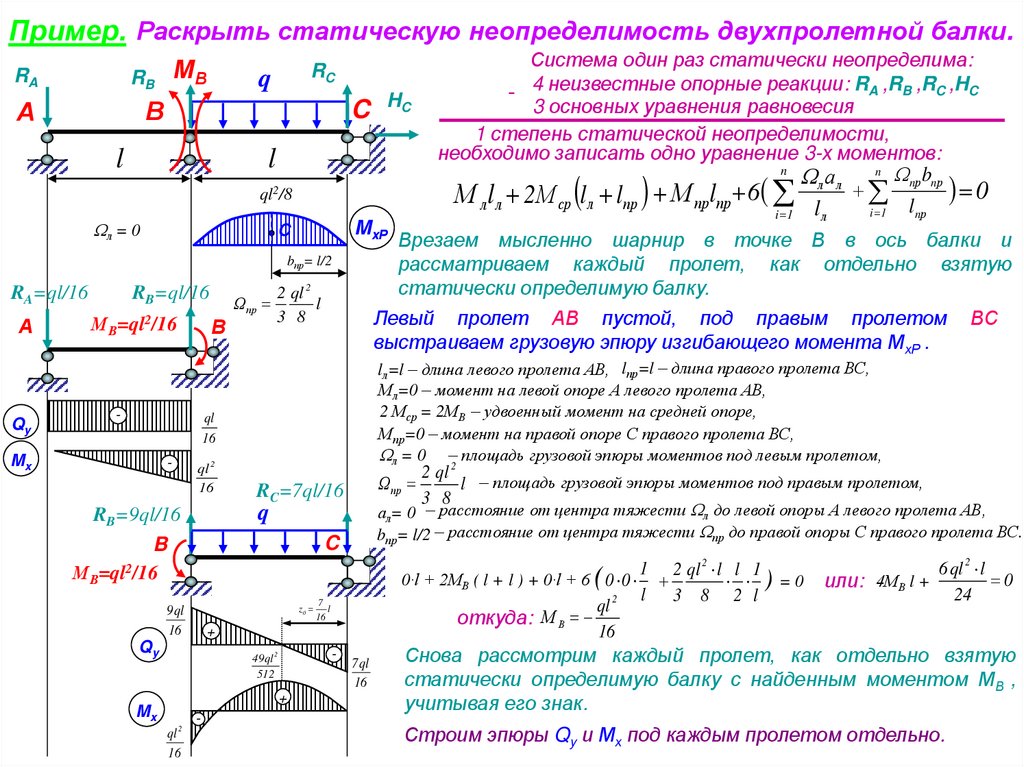
Пример. Раскрыть статическую неопределимость двухпролетной балки.
RA
МВ
RB
RC
q
В
А
C
l
HC
l
ql2/8
л = 0
MxР
C
bпр= l/2
RA=ql/16
А
Qy
RB=ql/16
МВ=ql2/16
Ωпр
В
-
2 ql 2
l
3 8
-
ql 2
16
(
0·l + 2МВ ( l + l ) + 0·l + 6 0 0
z0
-
49 ql 2
512
+
ql 2
16
ql 2
откуда: М В
16
7
l
16
+
-
ВС
2 ql
l – площадь грузовой эпюры моментов под правым пролетом,
3 8
ал= 0 – расстояние от центра тяжести л до левой опоры А левого пролета АВ,
bпр= l/2 – расстояние от центра тяжести пр до правой опоры С правого пролета ВС.
C
Qy
Mx
Врезаем мысленно шарнир в точке В в ось балки и
рассматриваем каждый пролет, как отдельно взятую
статически определимую балку.
Ωпр
RC=7ql/16
B
МВ=ql2/16
9 ql
16
lл=l – длина левого пролета АВ, lпр=l – длина правого пролета ВС,
Мл=0 – момент на левой опоре А левого пролета АВ,
2 Мср = 2МВ – удвоенный момент на средней опоре,
Мпр=0 – момент на правой опоре С правого пролета ВС,
л = 0 –2 площадь грузовой эпюры моментов под левым пролетом,
q
RB=9ql/16
Левый пролет АВ пустой, под правым пролетом
выстраиваем грузовую эпюру изгибающего момента МхР .
ql
16
Mx
Система один раз статически неопределима:
- 4 неизвестные опорные реакции: RA ,RB ,RC ,HC
3 основных уравнения равновесия
1 степень статической неопределимости,
необходимо записать одно уравнение 3-х моментов:
n
л а л n nр bnр
0
М лl л 2 М ср l л lпр М прlпр 6
lnр
lл
i 1
i 1
7 ql
16
1 2 ql 2 l l 1
) =0
l 3 8 2 l
6 ql 2 l
0
или: 4МВ l +
24
Снова рассмотрим каждый пролет, как отдельно взятую
статически определимую балку с найденным моментом МВ ,
учитывая его знак.
Строим эпюры Qy и Мх под каждым пролетом отдельно.

20.

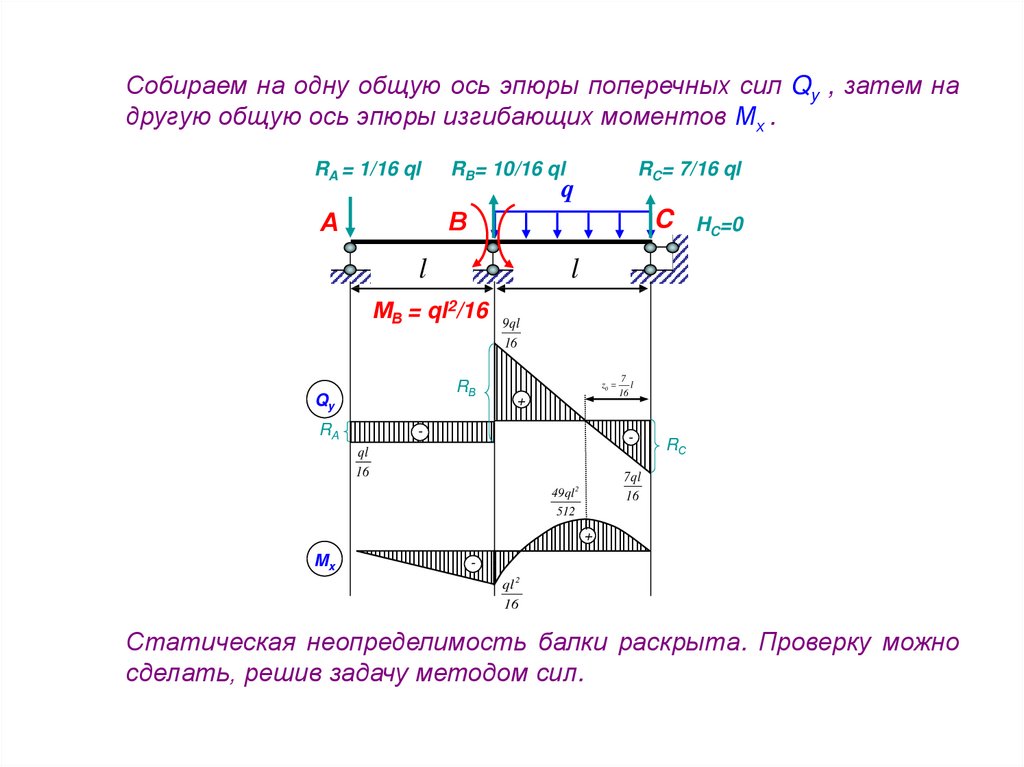
Собираем на одну общую ось эпюры поперечных сил Qy , затем на
другую общую ось эпюры изгибающих моментов Мх .
RA = 1/16 ql
RB= 10/16 ql
А
В
C
l
RВ
RA
HC=0
l
МВ = ql2/16
Qy
RC= 7/16 ql
q
9 ql
16
z0
+
-
7
l
16
-
ql
16
RС
7 ql
16
49 ql 2
512
+
Mx
ql 2
16
Статическая неопределимость балки раскрыта. Проверку можно
сделать, решив задачу методом сил.