Похожие презентации:
Тема 5. Вступ до математичного аналізу. Лекція №11. Неперервність функції. Визначні границі
1. Тема 5. Вступ до математичного аналізу
Лекція №11.Неперервність функції.
Визначні границі.
2. План
Неперервність функції у точці.Точки розриву та їх класифікація
Визначні границі
Еквівалентні величини
3. Означення 1.
4. Означення 2.
5. Означення
6.
7.
ТеоремаПравило обчислення границь
8. I теорема Вейерштрасса
9. II теорема Вейерштрасса
10. Теорема (про проміжне значення)
11. Означення.
Точка, в якій порушується хоча б одназ умов неперервності функції,
називається точкою розриву, а сама
функція називається розривною в
цій точці.
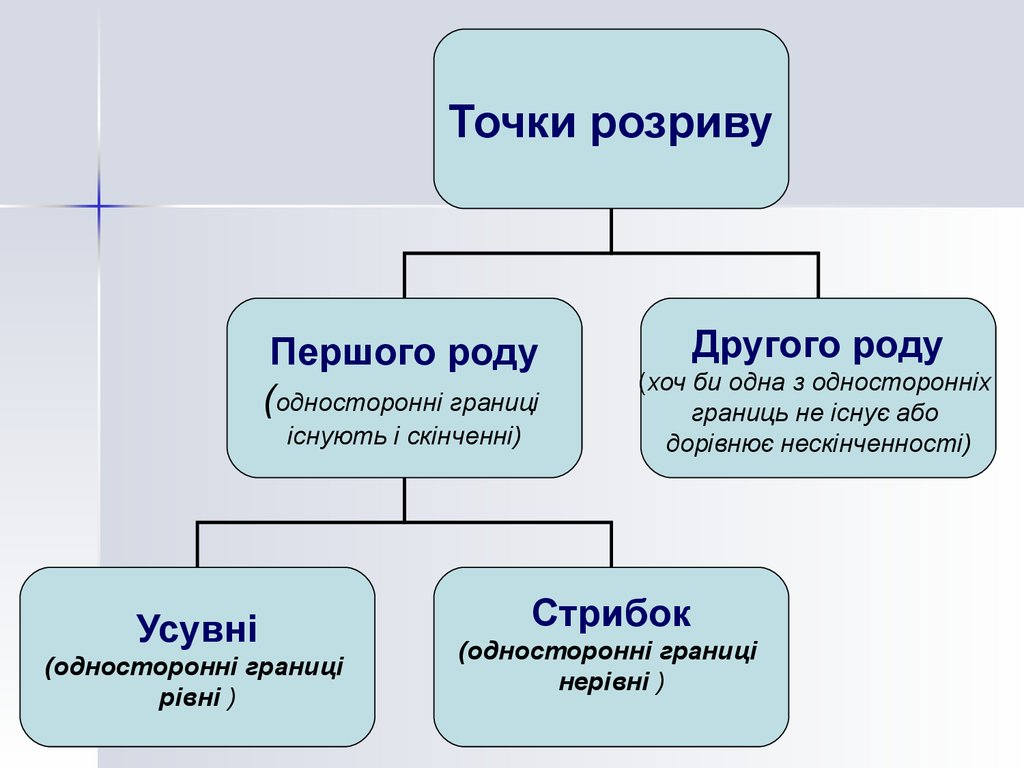
12.
Точки розривуПершого роду
(односторонні границі
існують і скінченні)
Усувні
(односторонні границі
рівні )
Другого роду
(хоч би одна з односторонніх
границь не існує або
дорівнює нескінченності)
Стрибок
(односторонні границі
нерівні )
13.
sin xy
.
x
sin x
sin x
x
0,1745
0,1736
0,9948
5
0
0,0873
0,0872
0,9988
2
0
0,0349
0,0349
1,0
0
0,0175
0,0175
1,0
градусний радіанний
вимір x
вимір
x
10
1
0
14. Перша визначна границя
Границя відношення синусанескінченно малої дуги до самої
дуги, вираженої в радіанах,
дорівнює 1, тобто
sin x
lim
1
x 0
x
15.
1f ( x ) 1
x
x
16. Друга визначна границя
x1
Границя функції f ( x) 1 як
x
При x , так і при x дорівнює
числу e , тобто
x
1
lim 1 e,
x
x
x
1
lim 1 e
x
x
1
x
lim 1 x e
x 0
17.
18.
19.
таблиця еквівалентнихнескінченно малих
якщо (x) 0 при x x0 , то
sin ( x) ~ ( x)
ln 1 ( x) ~ ( x)
tg ( x) ~ ( x)
a ( x ) 1 ~ ( x) ln a
arcsin ( x) ~ ( x)
arctg ( x) ~ ( x)
e ( x ) 1 ~ ( x)
( x)
log a 1 ( x) ~
ln a
( x) 2
1 cos ( x) ~
2
20. Теорема.
Границя відношення двох нескінченномалих функцій в точці x x1
дорівнює границі відношення двох
еквівалентних до них функцій в
точці x x1
21. Наслідки першої визначної границі
tg x1) lim
1
x 0 x
arcsin x
3) lim
1
x 0
x
1 cos x
2) lim
1
x 0 x 2 2
arctg x
4) lim
1
x 0
x
22. Наслідки другої визначної границі
ln(1 x )1) lim
1
x 0
x
log a (1 x )
2) lim
1
x 0
x ln a
x
e 1
3) lim
1
x 0
x
x
a 1
4) lim
1
x 0 x ln a
23. Завдання на самопідготовку
Шумко Л.І. , Шумко Л.Г.Вища математика, курс лекцій, 2005. .






















 Математика
Математика








