Похожие презентации:
Обчислення границь функцій. Перша та друга важливі границі
1.
Тема: Обчислення границь функцій.Перша та друга важливі границі.
2.
1. Обчислення границь функцій.У найпростіших випадках знаходження
lim f ( x ) зводиться до
границі x
x0
підстановки у функцію f (x) граничного
значення аргументу x0. Але часто така
підстановка приводить до невизначених
виразів.
Операцію знаходження границі у цих
випадках називають розкриттям
невизначеності.
3.
1. Невизначеність вигляду , щозадана відношенням двох многочленів.
Щоб знайти границю при х , тобто
f ( x)
lim
x g ( x )
треба чисельник і знаменник дробу
розділити на xk, де k – найвищій степінь
цих многочленів, і використати що
lim
1
x x к
0
4.
Приклад. Знайти границю3x 2 x 4
lim
x 2 3x 4 x 3
3
2
Розв’язання. Маємо невизначеність
вигляду .
Для знаходження границі поділимо
чисельник і знаменник дробу на x3
5.
2 43 3
3
2
3x 2 x 4
x
x
lim
lim
3
x 2 3x 4 x
x 2 3 4
3
2
x x
1
1
3 2 lim 4 lim 3
3
x x
x x
1
1
4
2 lim 3 3 lim 2 4
x x
x x
6.
02. Невизначеність вигляду 0 , що
задана відношенням двох многочленів.
Щоб знайти границю при х х0 , тобто
f ( x) 0
lim
x x g ( x)
0 , треба в чисельнику і
знаменнику виділити критичний множник
x – x0 і скоротити на нього дріб.
0
7.
Приклад. Знайтиx 8
lim 2
x 2 x 2 x 8
3
Розв’язання. Підставляючи значення
x0 = – 2 у вирази, які стоять у чисельнику і
знаменнику дробу, переконуємося, що
0
маємо невизначеність вигляду 0
8.
Виділяємо у чисельнику і в знаменникукритичний множник x – x0, тобто x + 2:
x 3 + 8 = (x + 2)(x2 – 2x + 4);
х 2 – 2x – 8 = (x + 2)(x – 4).
9.
x 8( x 2)( x 2 x 4)
0
lim 2
lim
x 2 x 2 x 8
0 x 2 ( x 2)( x 4)
3
x 2x 4
lim
2 .
x 2
x 4
2
2
10.
03. Невизначеність вигляду 0 , що
задана ірраціональними виразами
При знаходженні границі виразів з
ірраціональностями використовують
такий прийом: переведення
ірраціональності із знаменника в
чисельник або, навпаки, з чисельника в
знаменник (домноження чисельника і
знаменника на вираз, спряжений
ірраціональності).
11.
4. Розкриття невизначеностей вигляду; 0
При розкритті цих невизначеностей їх
попередньо зводять до невизначеностей
0
вигляду або
0
12.
Приклад. Знайти границюlim ( x( x 1) x )
x
Розв’язання. Маємо невизначеність
вигляду . Домножимо і
поділимо вираз
x( x 1) х на
спряжений, тобто на
x( x 1) x
13.
lim ( x( x 1) x) ( )x
lim
x
( x( x 1) x)( x( x 1) x)
x( x 1) x
x( x 1) x
x
lim
lim
2
x
x
x( x 1) x
x х x
2
14.
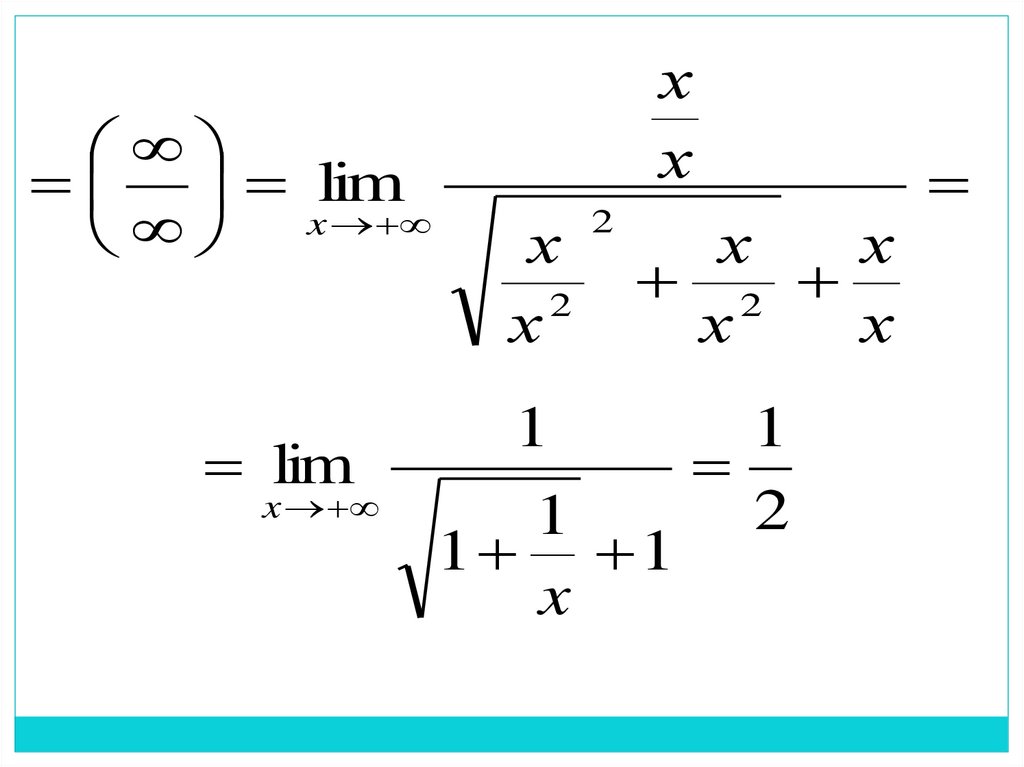
limx
lim
x
х
х
х
2
х
2
х
х
2
х
х
1
1
1 1
x
1
2
15.
2. Перша та друга важливі границі.0
Невизначеності виду 0 , задані
виразами, що містять тригонометричні
функції, часто розкривають за допомогою
першої важливої границі:
sin x
lim
1
x 0
x
16.
Наслідки.sin kx
1. lim
k ( k const )
x 0
x
sin kx
k
2. lim
(k , m сталі, m 0)
x 0 sin mx
m
17.
tg x3. lim
1
x 0
x
arctg x
4. lim
1
x 0
x
arcsin x
5. lim
1
x 0
x
18.
1cos
x
Приклад. Знайти lim
2
x 0
x
Розв’язання.
1 cos x 0
lim
2
x 0
x
0
x
x
2 x
2 sin
2 sin sin
1
2
2
2
lim
lim
2
x 0
x 0
x
x x
2
19.
Друга важлива границяx
1
lim 1 e
x
x
використовується при розкритті
невизначеності 1
Трансцендентне число е наближено
дорівнює е ≈2,71184….. і його називають
числом Ейлера.
20.
Наслідки.1
х
1. lim(1 х) e
х 0
x
k
k
2. lim 1 e
x
x
1
х
3. lim(1 kх) e
х 0
k
21.
3. Порівняння нескінченно малих.Дві нескінченно малі функції
порівнюються між собою за допомогою
дослідження їхнього відношення. Нехай
(x) і (x) – нескінченно малі функції при
х х0 , тобто lim ( x) 0, lim ( x) 0
x x0
x x0
22.
1. Якщо( x)
lim
C 0 (C = const),
x x ( x)
0
то функції (x) і (x) називаються
нескінченно малими одного порядку
при х х0
23.
( x)0,
2. Якщо xlim
x ( x)
0
то функція (x) називається нескінченно
малою вищого порядку ніж (x) при
х х0
24.
( x),
3. Якщо xlim
x ( x)
0
то функція (x) називається нескінченно
малою нижчого порядку, ніж (x) при
х х0
25.
( x)C
4. Якщо lim
,
k
x x0 [ ( x)]
де k > 0 і С 0 – сталі, то функцію (x)
називають нескінченно малою k-го
порядку відносно (х) при х х0
26.
5. Нескінченно малі функції (x) і (x)називаються непорівнянними при х х0 ,
якщо в точці x0 не існує границі їхнього
відношення.
27.
( x )1,
6. Якщо xlim
x0 ( x )
то нескінченно малі (x) та (x) називаються еквівалентними нескінченно
малими при х х0 . Позначається це
так:
(x) ~ (x).
28.
Властивості еквівалентних нескінченномалих функцій.
Теорема. Нескінченно малі функції (x)
та (x) еквівалентні при х х0 тоді і
тільки тоді, коли різниця (x) – (x) є
нескінченно малою функцією вищого
порядку, ніж кожна з функцій (x) та (x).
29.
Теорема. Нехай (x) ~ 1(x), (x) ~ 1(x)при х х0 . Якщо існує границя
1 ( x )
( x)
lim
lim
,
то
існує
і
границя
x x x ,
x x x
0
0
і ці границі рівні:
( x)
1 ( x )
lim
lim
x x x
x x x
0
0
30.
Еквівалентні нескінченно малівеличини.
Нехай lim ( x) 0 , тобто (x) є
x x0
нескінченно малою функцією при х х0
Тоді мають місце наступні
еквівалентності в околі точки х х0
31.
sin ~arcsin ~
tg ~
arctg ~
1 cos ~
2
e 1~
2
ln 1 ~
log a 1 ~ log a e






























 Математика
Математика








