Диференційне числення функції однієї змінної

1. ВИЩА МАТЕМАТИКА

для студентів ОС “Бакалавр”
ОПП:
122 “Комп’ютерні науки”
Автор:
Доцент кафедри комп’ютерних наук, к.е.н.
Сирмаміїх Ірина Вікторівна

2. Диференційне числення функції однієї змінної

Тема
1.
Тема 2.
Тема 3.
Поняття похідної функції, її
геометричний та механічний зміст. Основні
правила і формули диференціювання. Похідна
складеної функції.
Неявно задана функція та її похідна.
Логарифмічне
диференціювання.
Похідна
показниково-степеневої функції. Похідна функції,
заданої параметрично.
Диференціал функції. Застосування
диференціала в наближених обчисленнях.

3. Диференційне числення функції однієї змінної

Тема 4.
Тема
5.
Тема
6.
Похідні вищих порядків. Диференціали
вищих порядків.
Застосування
числення до знаходження
Правила Лопіталя.
диференціального
границі функції.
Застосування диференціального
числення для дослідження функцій і побудови їх
графіків

4. Інформаційні ресурси в Інтернеті

1.
2.
3.
Вища математика: Підручник / Домбровський В.А., Крижанівський І.М.,
Мацьків Р.С., Мигович Ф.М., Неміш В.М., Окрепкий Б.С., Хома Г.П.,
Шелестовська М.Я.; за редакцією Шинкарика М.І. –Тернопіль:
Видавництво Карп’юка, 2003 - 480с. - ISBN 966-7946-15-0 [Електронний
ресурс]. – Режим доступу:
http://library.tneu.edu.ua/files/EVD/matematica/VM_pidr.pdf. - Назва з
екрану.
Вища математика. Навчальний посібник. [Електронний ресурс]. – Режим
доступу: http://univer.nuczu.edu.ua/tmp_metod/148/Basmanov.pdf - Назва з
екрану.
Рубiш В.В. Конспект лекцiй з курсу "Вища математика": Частина I. –
Ужгород: ДВНЗ УжНУ, 2015. – 96 с. [Електронний ресурс]. – Режим
доступу:
https://dspace.uzhnu.edu.ua/jspui/bitstream/lib/3472/1/Methodychka_VM_Phy
s.pdf

5. Тема1: Поняття похідної функції. Основні правила та формули диференціювання. Похідна складеної функції

1. Означення похідної
2. Геометричний зміст похідної
3. Механічний зміст похідної
4. Залежність між неперервністю
і диференційовністю функції
5. Основні правила диференціювання
6. Похідні від основних елементарних
функцій.
7. Похідна складеної функції

6. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ

Поняття похідної є одним з основних понять
математичного аналізу.
Розділ математики, в якому вивчається поняття
похідної та її застосування до дослідження
функцій,
називають
диференціальним
численням.

7. ОСНОВОПОЛОЖНИКИ ДИФЕРЕНЦІАЛЬНОГО ЧИСЛЕННЯ

І. Ньютон
Г. Лейбніц

8. ЗАДАЧІ, ЩО ПРИВЕЛИ ДО ПОНЯТТЯ ПОХІДНОЇ

ЗАДАЧІ
про миттєву
швидкість
про дотичну
до кривої

9. Означення похідної

y
y=f(x)
f(x0+ x)
f(x)
f(x0)
0
x0
x
x0+ x x
Графічне зображення приросту
функції і приросту аргументу.
Похідною від функції
y=f(x) за аргументом
х називається границя
відношення приросту
функції до приросту
аргументу,
коли
приріст
аргументу
прямує до нуля:
f ( x0 x) f ( x0 )
f ( x) lim
x 0
x
dy
dx

10. Означення похідної (аналітичний вигляд)

f x x f x
y
y lim
lim
x 0 x
x 0
x

11. ПОЗНАЧЕННЯ ПОХІДНОЇ

y , y x , f x ,
позначення
Лагранжа
dy df x d
,
, f x
dx
dx
dx
позначення
Лейбніца

12. ЗМІСТ ПОХІДНОЇ

ГЕОМЕТРИЧНИЙ
МЕХАНІЧНИЙ
ЕЛЕКТРИЧНИЙ

13.

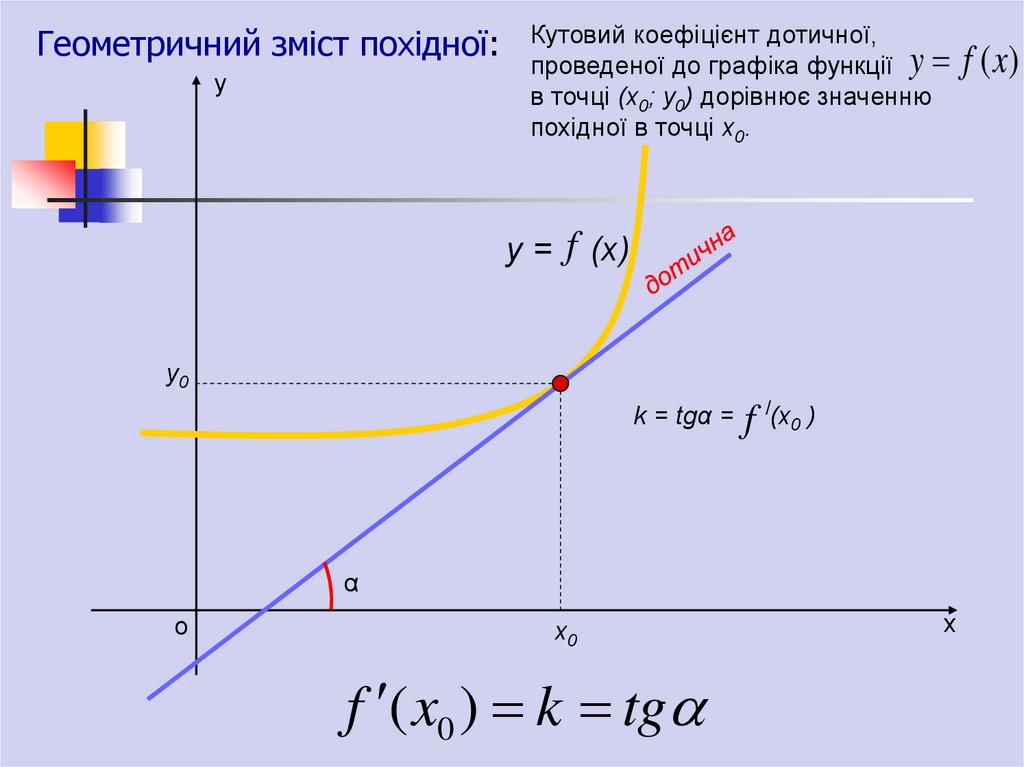
Геометричний зміст похідної:
у
Кутовий коефіцієнт дотичної,
проведеної до графіка функції y
в точці (х0; у0) дорівнює значенню
похідної в точці х0.
y = f (x)
у0
k = tgα =
f /(x0 )
α
о
х0
f ( x0 ) k tg
х
f ( x)

14.

Рівняння дотичної і нормалі до
кривої у = f (х) в точці М (х0 ; у0)
Дотичною до кривої в точці M називається граничне положення січної, якщо точки
січної необмежено наближається вздовж кривої до точки M
Нормаллю до кривої (або поверхні) в заданій точці M називається пряма (або
площина), яка проходить через цю точку і перпендикулярна до дотичної прямої
(або площини) в цій точці кривої (поверхні).

15. Механічний зміст похідної функції

Нехай функція
y f ( x) S (t )
описує деякий фізичний процес:
х0 – координата точки
v(t0)- швидкість точки в момент
часу t0
а(t0) – прискорення точки в момент
часу t0

16. Механічний зміст похідної функції

S (t0 ) (t0 ) lim
t 0
S
t
S (t0 ) (t0 ) a(t0 )
-
миттєва швидкість
- прискорення
•Миттєва швидкість прямолінійного руху
дорівнює похідній шляху за часом руху
•Похідна від швидкості по часу(або друга
похідна від шляху) є прискоренням

17. ЕЛЕКТРИЧНИЙ ЗМІСТ ПОХІДНОЇ

Нехай Q Q(t ) - кількість електрики, яка
пройшла через поперечний переріз
провідника за час t . Сила струму i (t ) в
момент часу t є похідна від кількості
електрики Q(t ) по часу t , тобто
i (t ) Q (t )

18. Зв’язок між диференційовністю та неперервністю функції.

Означення. Функція у = f (x) називається
диференційовною на інтервалі (а; b), якщо вона
диференційовна в кожній точці даного інтервалу.

19. Зв’язок між диференційовністю та неперервністю функції.

Зв’язок між неперервністю і диференційовністю функції
встановлює теорема.
Теорема. Якщо функція диференційовна в деякій точці,
то у цій точці функція неперервна.
Обернене твердження неправильне: для неперервної функції
може не існувати похідної.
Наслідок. Якщо функція розривна в деякій точці, то вона не
має похідної в цій точці.
Висновок: необхідною умовою диференційовності функції
у = f (х) у точці х є її неперервність у цій точці.

20. Правила диференціювання

.
Теорема 2. Сталий множник можна виносити за знак
похідної:
(cu)'=cu', де с = const.
Теорема 3. Похідна алгебраїчної суми скінченної
кількості
диференційовних
функцій
алгебраїчній сумі похідних цих функцій:
(u ) u
дорівнює

21. Правила диференціювання

.
Теорема 4.
Похідна добутку двох диференційовних функцій
дорівнює добутку першого множника на похідну другого плюс
добуток другого множника на похідну першого:
(u ) u u
Теорема 5.
Якщо чисельник і знаменник дробу диференційовні функції
(знаменник не перетворюється в нуль), то похідна дробу також дорівнює
дробу, чисельник якого є різницею добутків знаменника на похідну
чисельника і чисельника на похідну знаменника, а знаменник є квадратом
знаменника початкового дробу:
u u u
2

22.

Похідні від основних
елементарних функцій
Похідна степеневої функції:
y x
n
y' n x
n
y x
y'
1
2 x

23.

Похідні від основних елементарних
функцій:
Похідна показникової функції
y a
x
y ' a ln a
x
y e
x
y' e
x

24.

Похідні від основних елементарних
функцій:
Похідна логарифмічних функцій
y log a x
y'
x ln a
y ln x
y'
x

25.

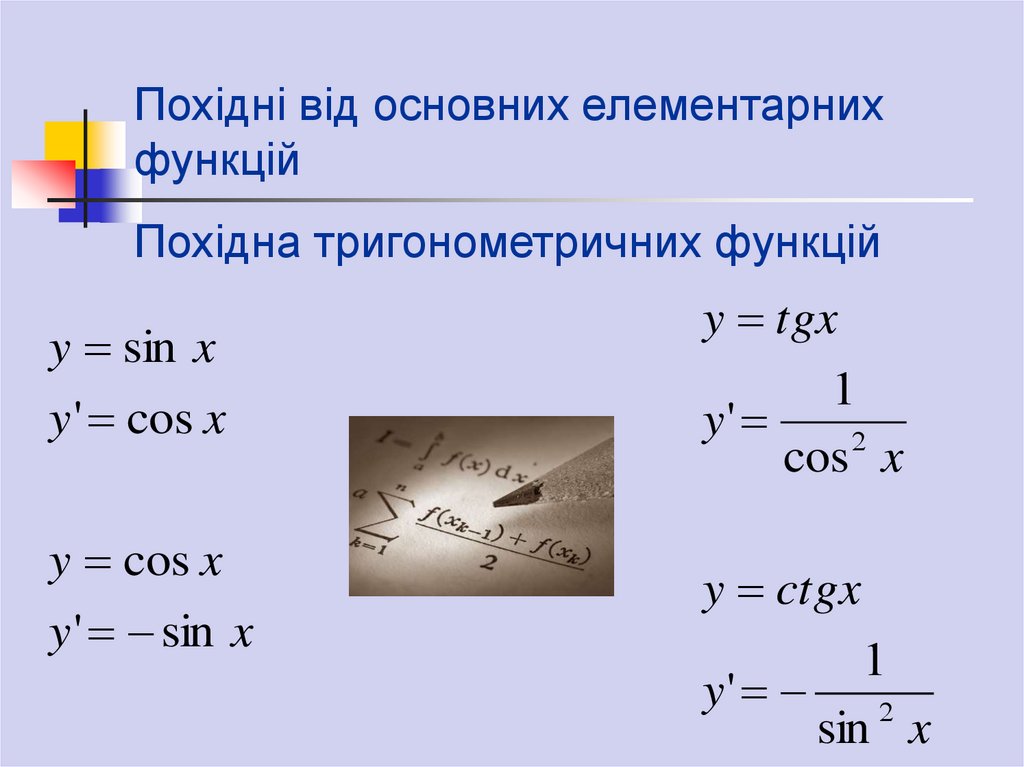
Похідні від основних елементарних
функцій
Похідна тригонометричних функцій
y sin x
y ' cos x
y cos x
y ' sin x
y tgx
y'
cos x
y ctgx
y'
sin x

26.

Похідні від основних елементарних функцій:
Похідні від обернених тригонометричних
функцій
y arctgx
y arcsin x
y'
y'
x
x
y arccos
y arcctgx
y'
x
y'
x

27. Приклади визначення похідної функції

№1
( y) ( x 2 sin x) ( x 2 ) (sin x) 2 x cos x
№2
1
1
( y ) ( x ln x) ( x ) ln x (ln x) x
ln x x
x
2 x
№3
( y) (
x
( x) cos x (cos x) x 1 cos x ( sin x) x cos x x sin x
)
2
2
cos x
cos x
cos x
cos2 x

28.

Похідна складеної функції

29. Приклади знаходження похідних складених функцій

№1
(cos 4 x) sin 4 x (4 x) 4 sin 4 x
№2
2
2
(cos 4 x) 3 cos 4 x (cos 4 x) 12 cos 4 x sin 4 x
3

30. Контрольні запитання

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
Означення похідної.
Алгоритм знаходження похідної за означенням.
Механічний зміст похідної.
Геометричний зміст похідної.
Електричний зміст похідної.
Залежність між неперервністю і диференційовністю функції.
Похідна суми.
Похідна добутку.
Похідна частки.
Похідна складеної функції.
x
Похідна функції y e .
Похідна функції y a x .
Похідна логарифмічної функції.
Похідна степеневої функції.
Похідні тригонометричних функцій.
Похідні обернених тригонометричних функцій.