Конус

1.

Конус

2.

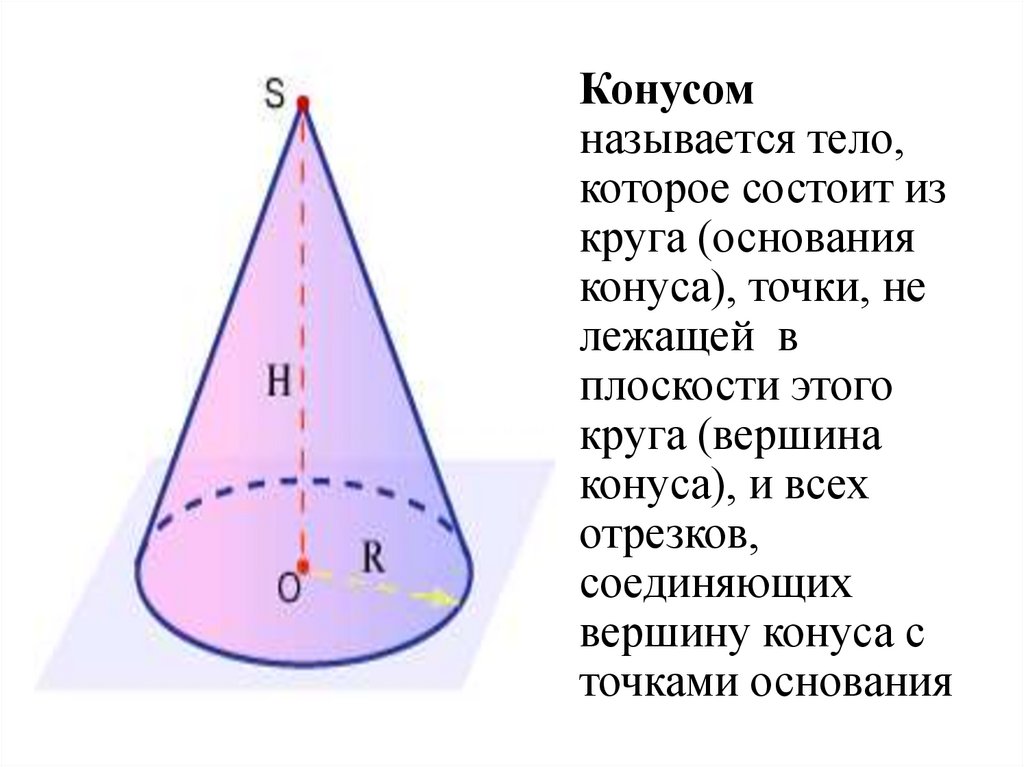
Конусом
называется тело,
которое состоит из
круга (основания
конуса), точки, не
лежащей в
плоскости этого
круга (вершина
конуса), и всех
отрезков,
соединяющих
вершину конуса с
точками основания

3.

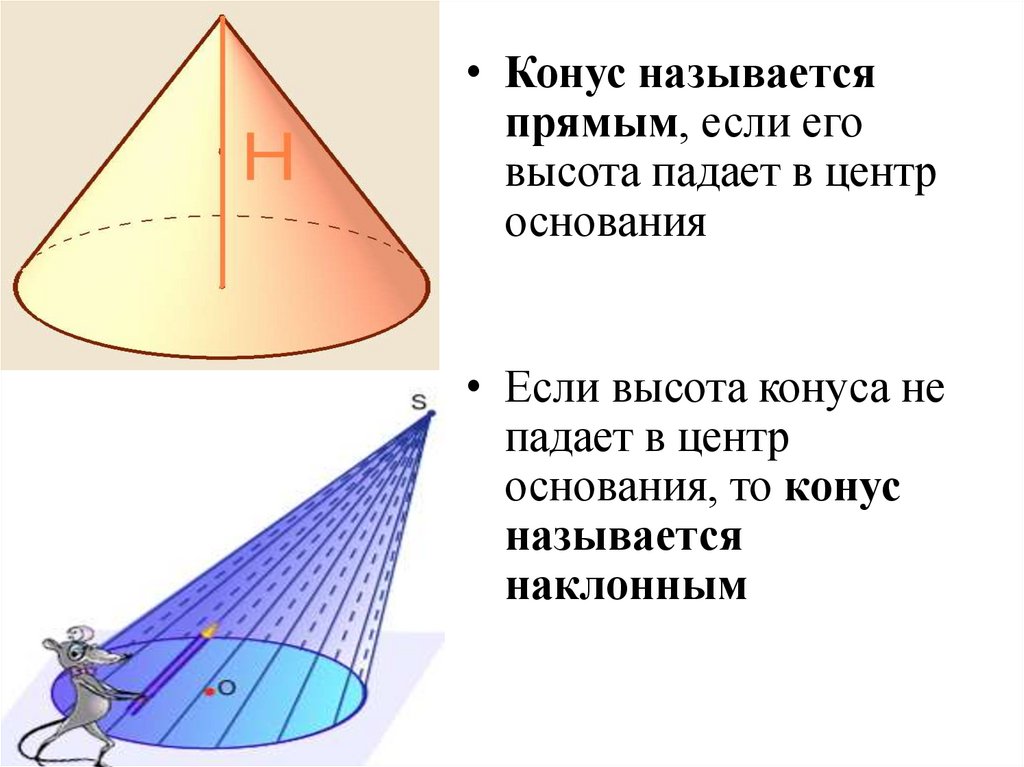
• Конус называется
прямым, если его
высота падает в центр
основания
• Если высота конуса не
падает в центр
основания, то конус
называется
наклонным

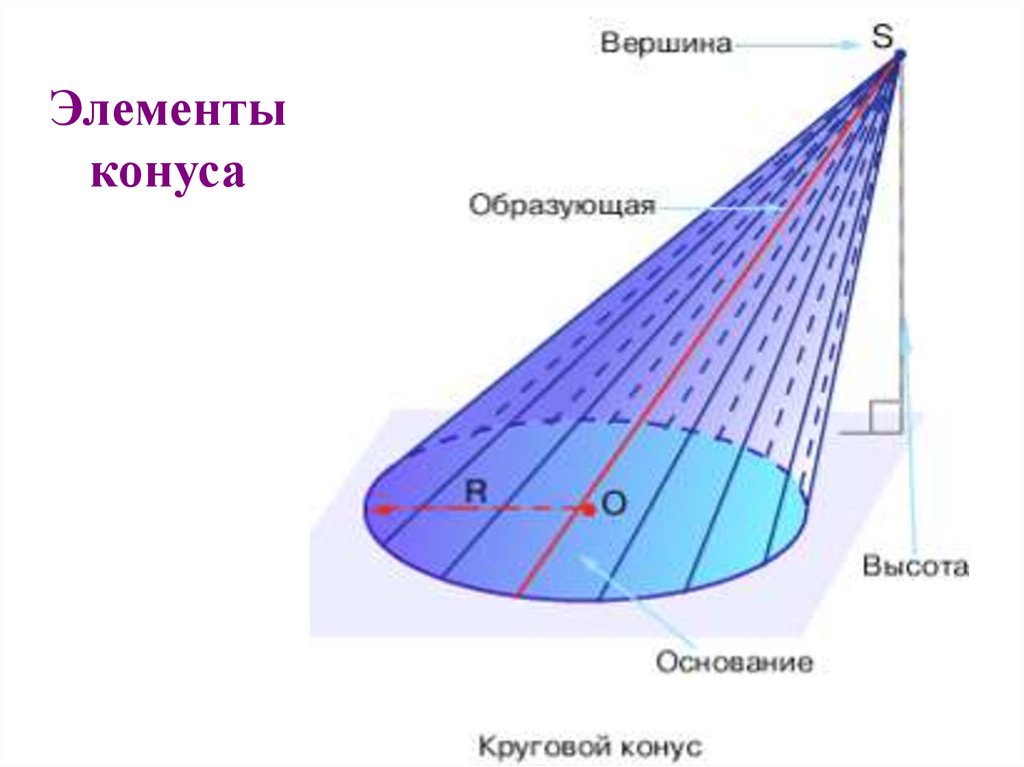
4. Элементы конуса

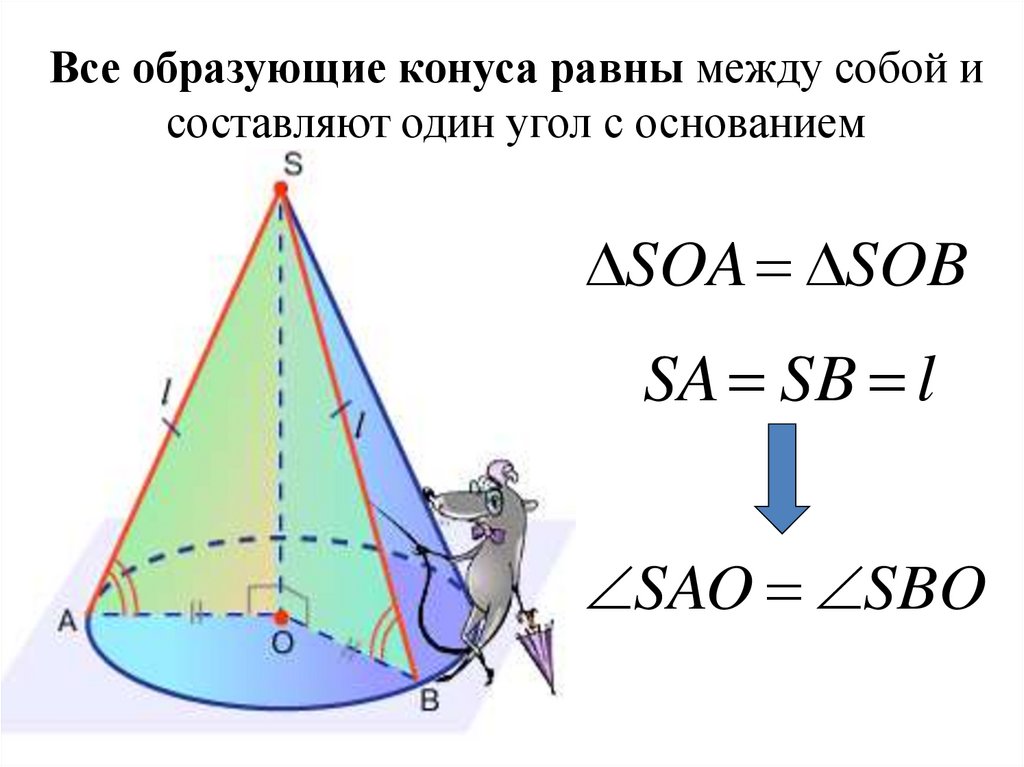
5. Все образующие конуса равны между собой и составляют один угол с основанием

SOA SOB
SA SB l
SAO SBO

6.

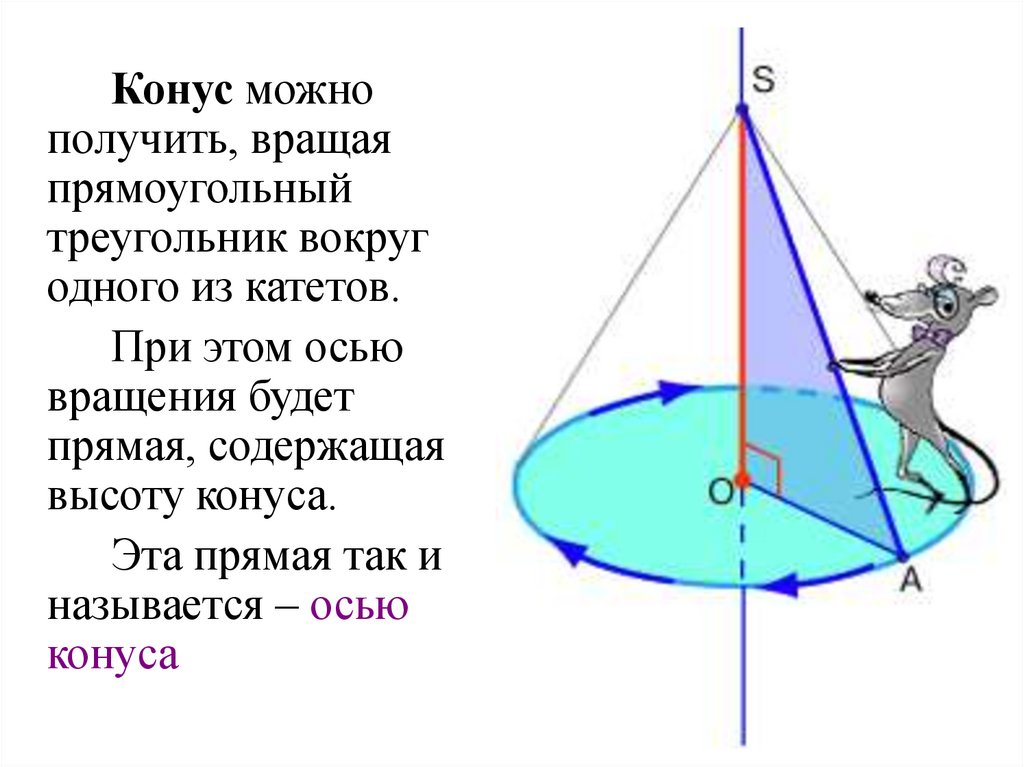
Конус можно
получить, вращая
прямоугольный
треугольник вокруг
одного из катетов.
При этом осью
вращения будет
прямая, содержащая
высоту конуса.
Эта прямая так и
называется – осью
конуса

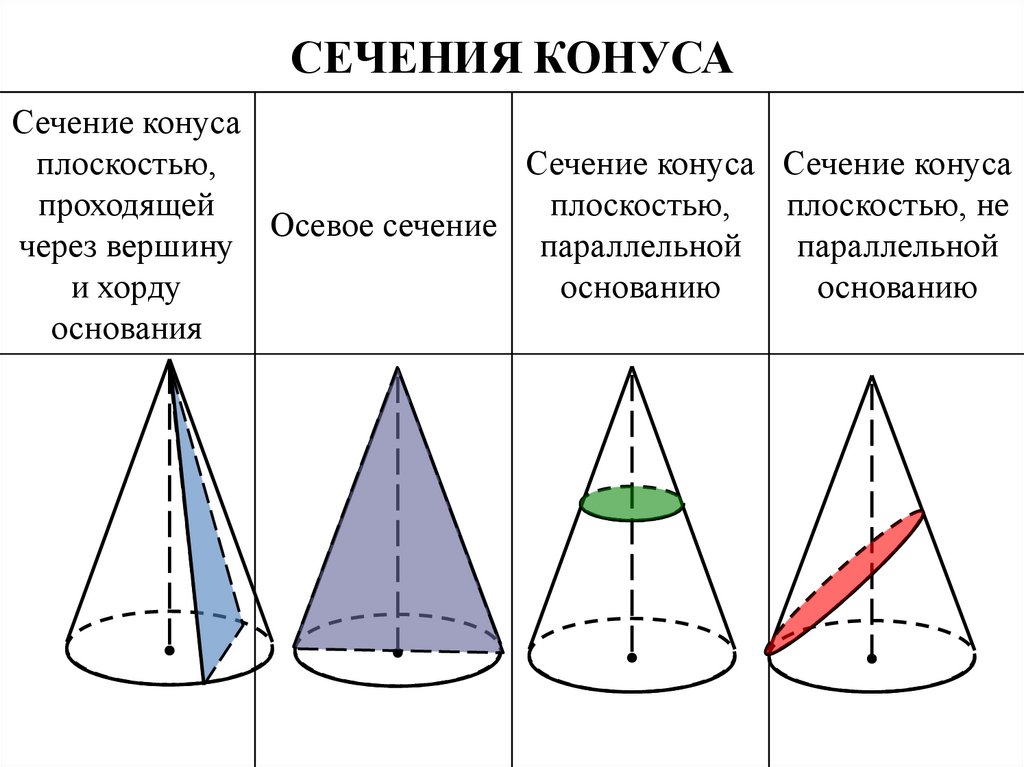
7. СЕЧЕНИЯ КОНУСА

Сечение конуса
плоскостью,
Сечение конуса Сечение конуса
проходящей
плоскостью,
плоскостью, не
Осевое сечение
через вершину
параллельной
параллельной
и хорду
основанию
основанию
основания

8.

Q
l=R
r
А‫׳‬
А
L=2πr
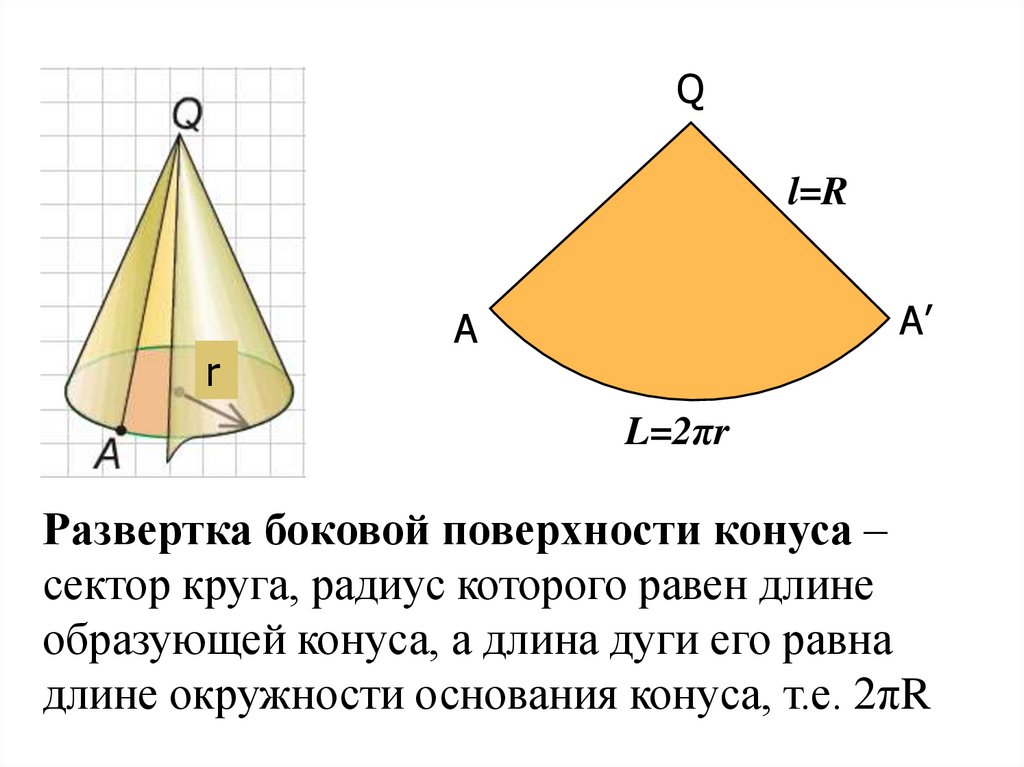
Развертка боковой поверхности конуса –
сектор круга, радиус которого равен длине
образующей конуса, а длина дуги его равна
длине окружности основания конуса, т.е. 2πR

9.

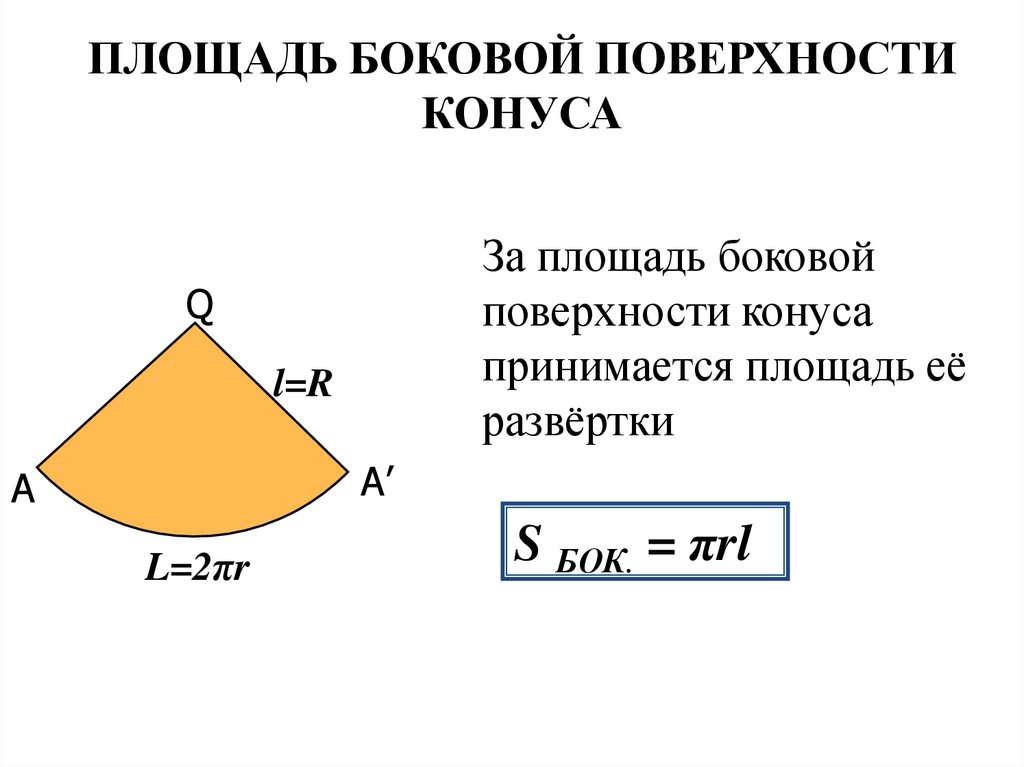
ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ
КОНУСА
За площадь боковой
поверхности конуса
принимается площадь её
развёртки
Q
l=R
А‫׳‬
А
L=2πr
S БОК. = πrl

10.

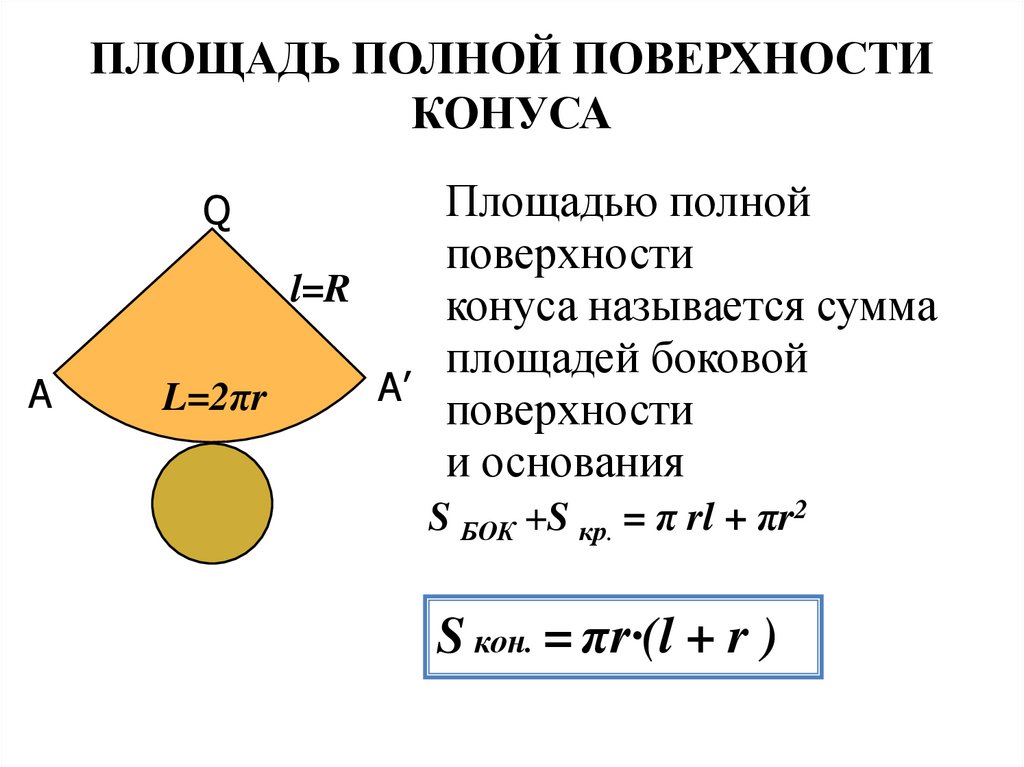
ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ
КОНУСА
Площадью полной
поверхности
l=R
конуса называется сумма
площадей боковой
А‫׳‬
L=2πr
поверхности
и основания
Q
А
S БОК +S кр. = π rl + πr2
S кон. = πr·(l + r )

11.

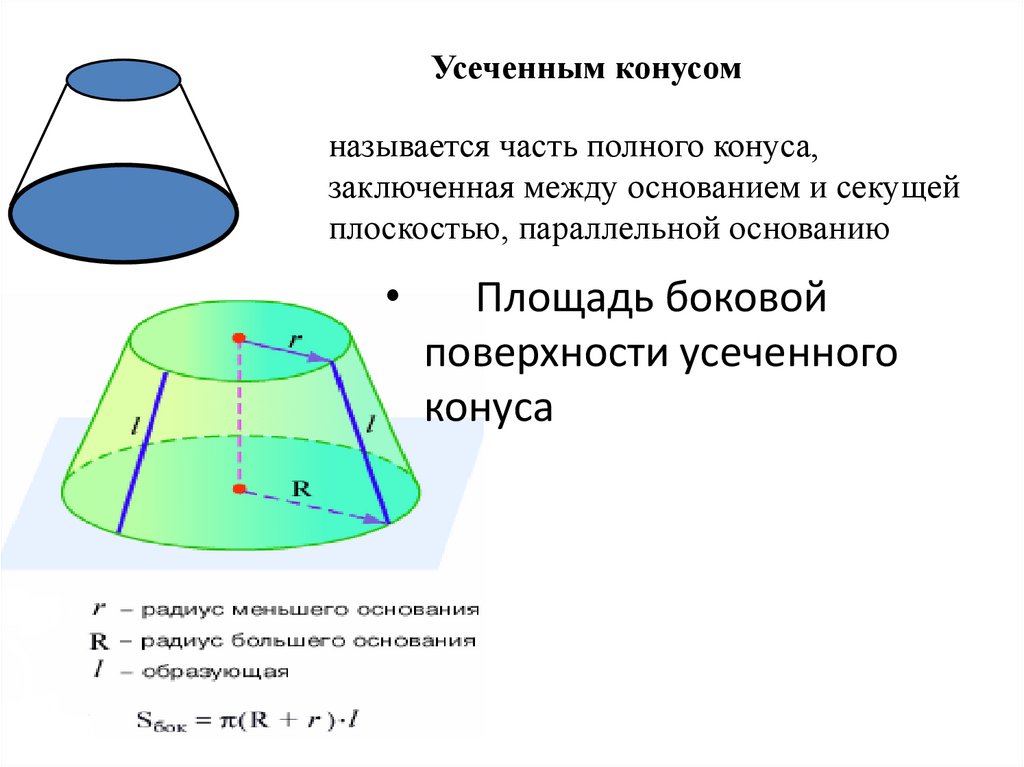
Усеченным конусом
называется часть полного конуса,
заключенная между основанием и секущей
плоскостью, параллельной основанию
Площадь боковой
поверхности усеченного
конуса

12.

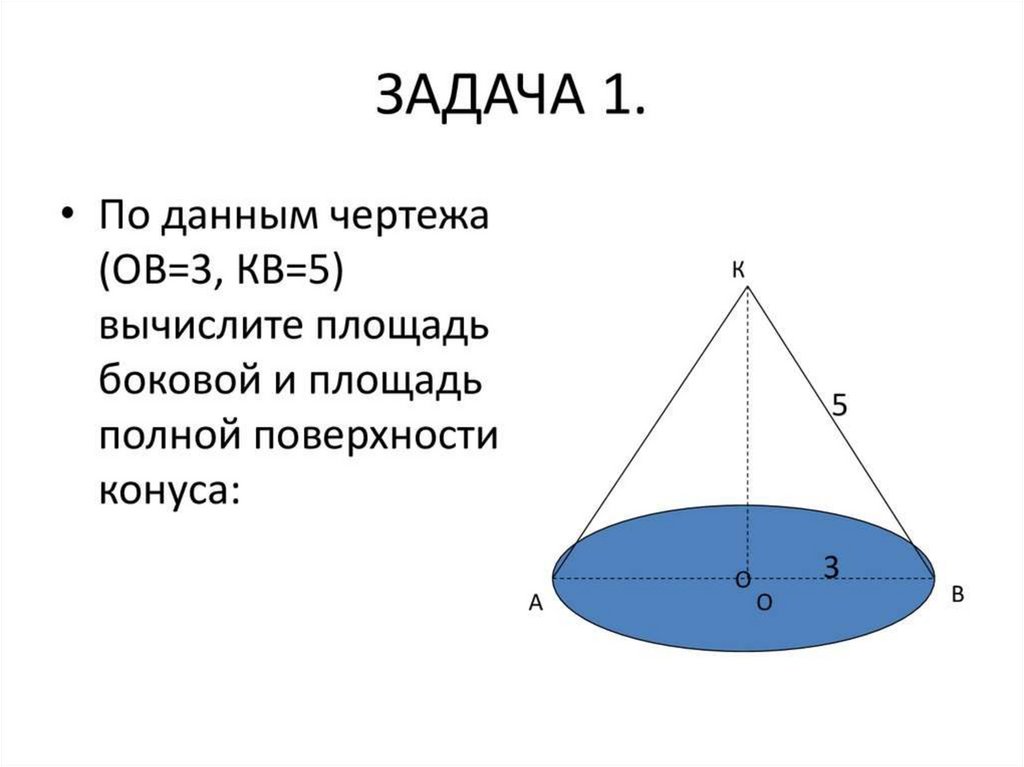
13.

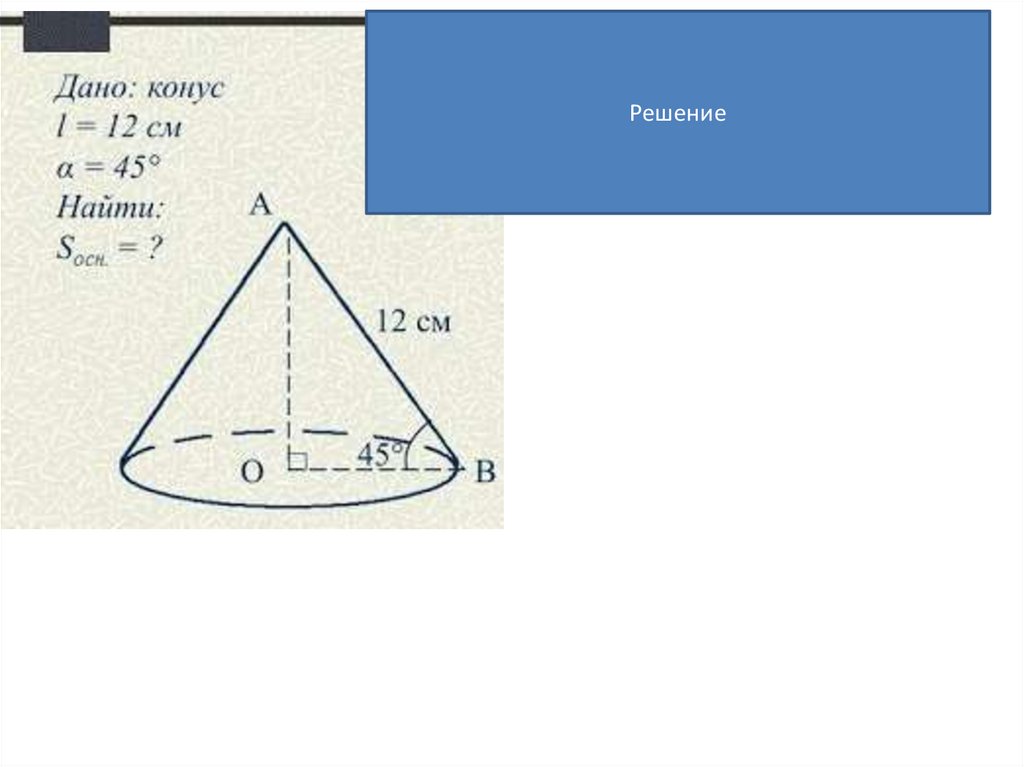
Решение

14.

Домашнее задание
ГЛ 3 п. 3 с 121-128
(формулы)
Задача № 4 с.129
(электронный учебник
с135 № 449