Функции и их свойства

1. Презентация к уроку в 9 классе

2.

Вспомнить определение функции;
Повторить свойства функций;
Применять знания о функциях для решения
заданий;
Подготовка к ГИА.

3. - это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами.

4.

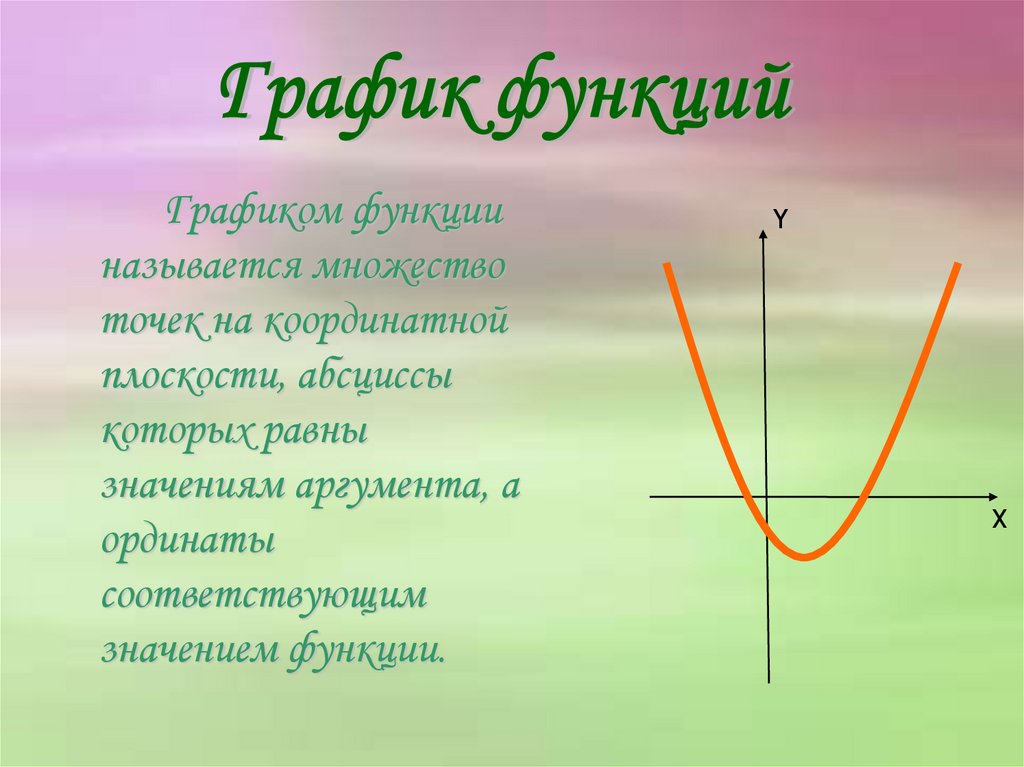
Графиком функции
называется множество
точек на координатной
плоскости, абсциссы
которых равны
значениям аргумента, а
ординаты
соответствующим
значением функции.
Y
X

5.

Существует несколько основных
видов функций:
линейная функция;
прямая пропорциональность;
обратная пропорциональность;
квадратичная функция;
кубическая функция;
функция корня;
функция модуля.
y
x

6.

- функция вида y=k x + b;
область определения функции –
вся числовая прямая: D
(f)=R; область значений
функции – вся числовая
прямая: E (f)=R; графиком
функции является прямая.
- Если k > 0, функция возрастает
- Если k < 0, функция убывает
y
x
y
x

7.

- функция вида y=k x ;
область определения
функции – вся числовая
прямая: D (f)=R; область
значений функции – вся
y
числовая прямая:
E (f)=R; графиком функции
является прямая,
проходящая через
начало координат.
x

8.

- функция вида y=k/x ; область
определения функции – от минус
бесконечности до нуля и от
нуля до бесконечности:
D (f)=(-∞;0)υ(0;∞) область
значений функции – вся
числовая прямая,
исключая нули:
E (f)=(-∞;0)υ(0;∞); графиком
функции является гипербола,
не проходящая через начало
координат.
y
k>0
x
y
k<0
x

9.

- функция вида y=kx³; область
определения функции – вся
числовая прямая: D (f)=R;
область значений функции – вся
числовая прямая: E (f)=R;
графиком функции является
кубическая парабола.
Если k>0, то график функции
расположен в I и III
координатных четвертях(она
возрастает, как на рисунке), а
если k<0, то II и IV
координатных четвертях( она
убывает)
y
x

10.

- функция вида y= x ;
область определения
функции – от нуля до
бесконечности: D
(f)=[0;∞); область
значений функции –от
нуля до
бесконечности: E
(f)=[0;∞); графиком
функции является ветвь
параболы.
y
x

11.

-
функция вида y=|x|;
область определения
функции – вся числовая
прямая: D (f)=R;
область значений функции
–от нуля до
бесконечности: E
(f)=[0;∞); график
функции зависит от под
модульного
выражения, но график
не может опускаться
ниже оси абсцисс.
y
x

12.

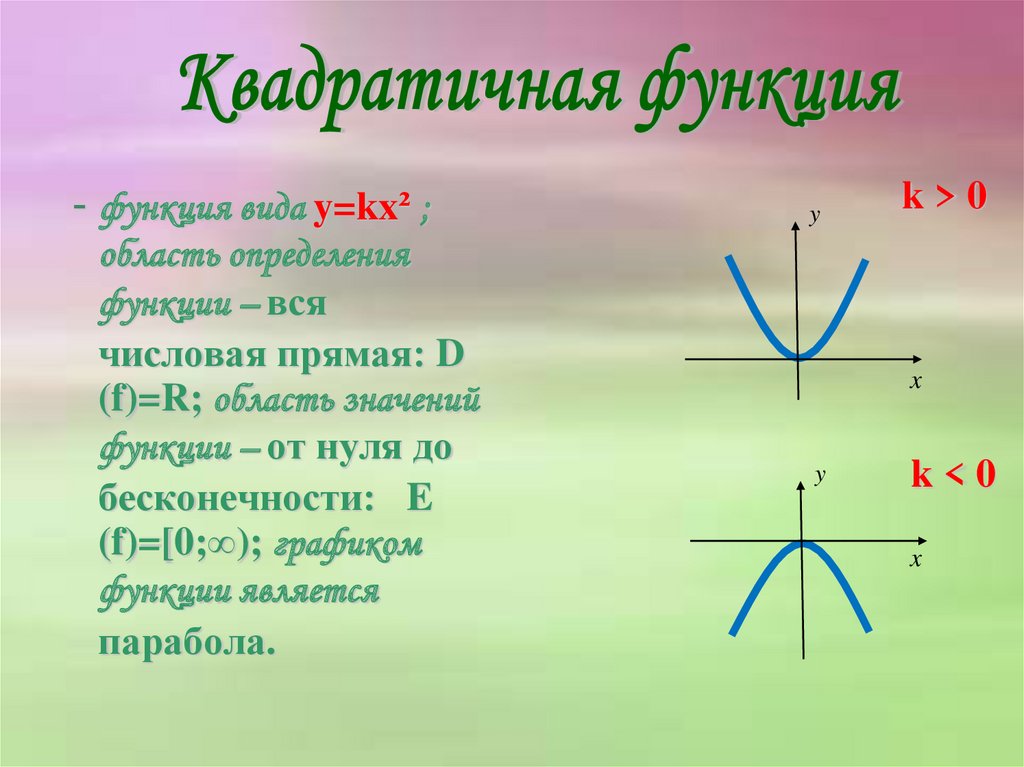
- функция вида y=kx² ;
область определения
функции – вся
числовая прямая: D
(f)=R; область значений
функции – от нуля до
бесконечности: E
(f)=[0;∞); графиком
функции является
парабола.
y
k>0
x
y
k<0
x

13.

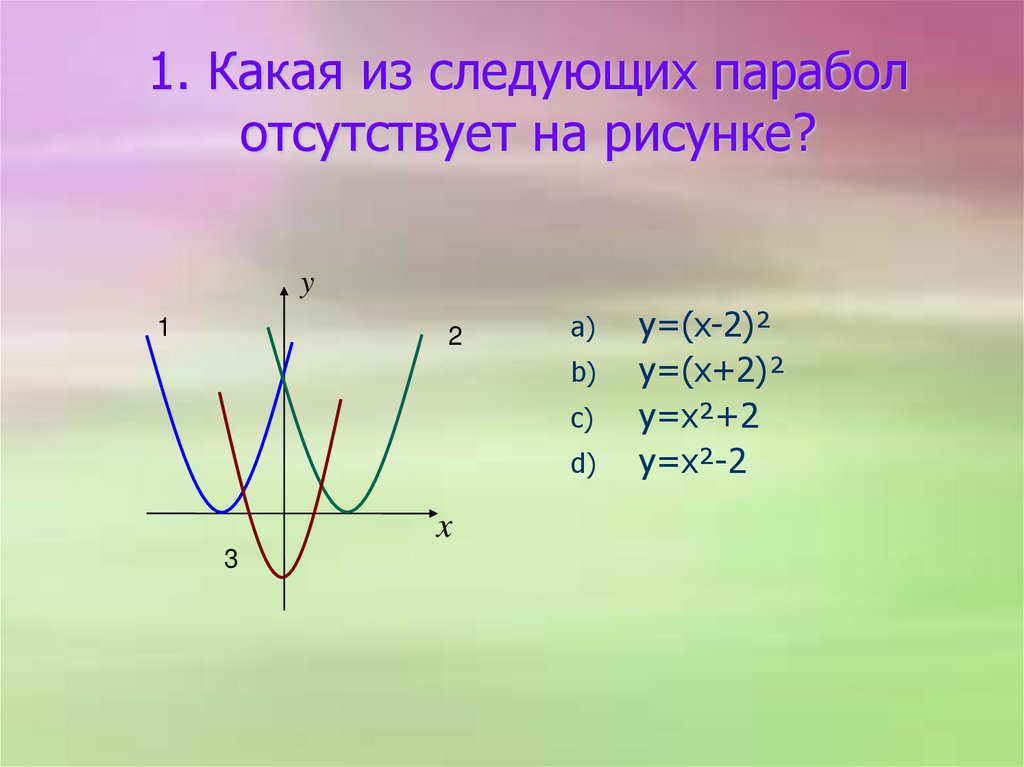
1. Какая из следующих парабол
отсутствует на рисунке?
y
1
2
a)
b)
c)
d)
x
3
y=(x-2)²
y=(x+2)²
y=x²+2
y=x²-2

14. 1. Какая из следующих парабол отсутствует на рисунке?

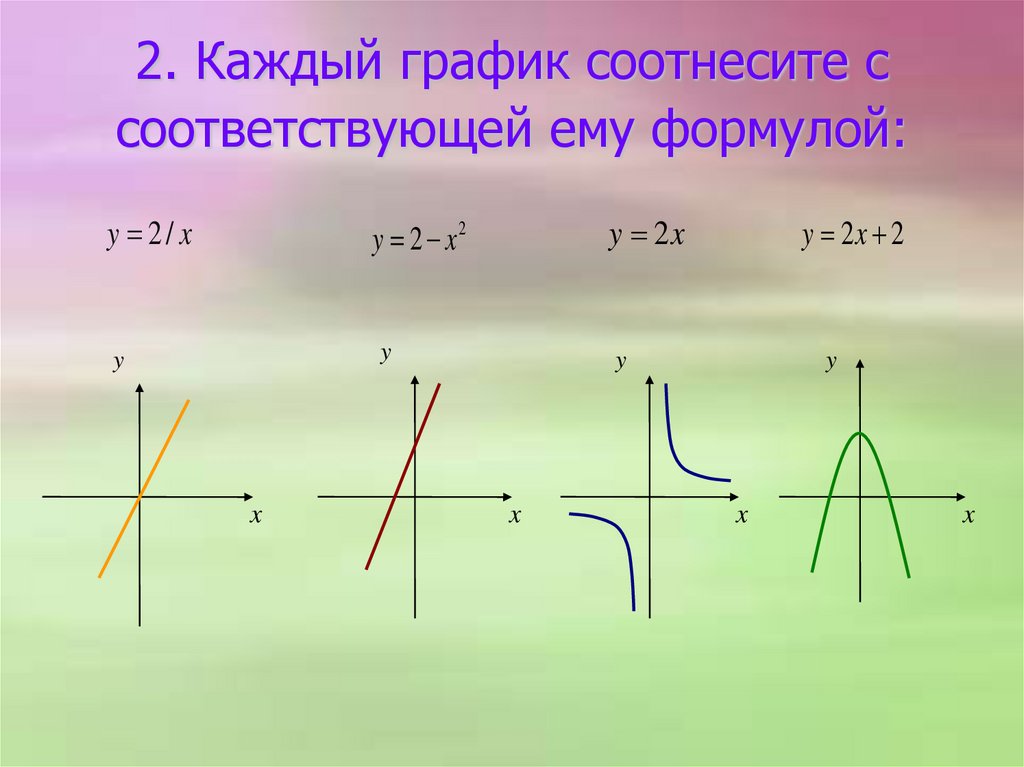
2. Каждый график соотнесите с
соответствующей ему формулой:
y 2/ x
y 2x
y 2 x2
y
y
x
y 2x 2
y
x
y
x
x

15. 2. Каждый график соотнесите с соответствующей ему формулой:

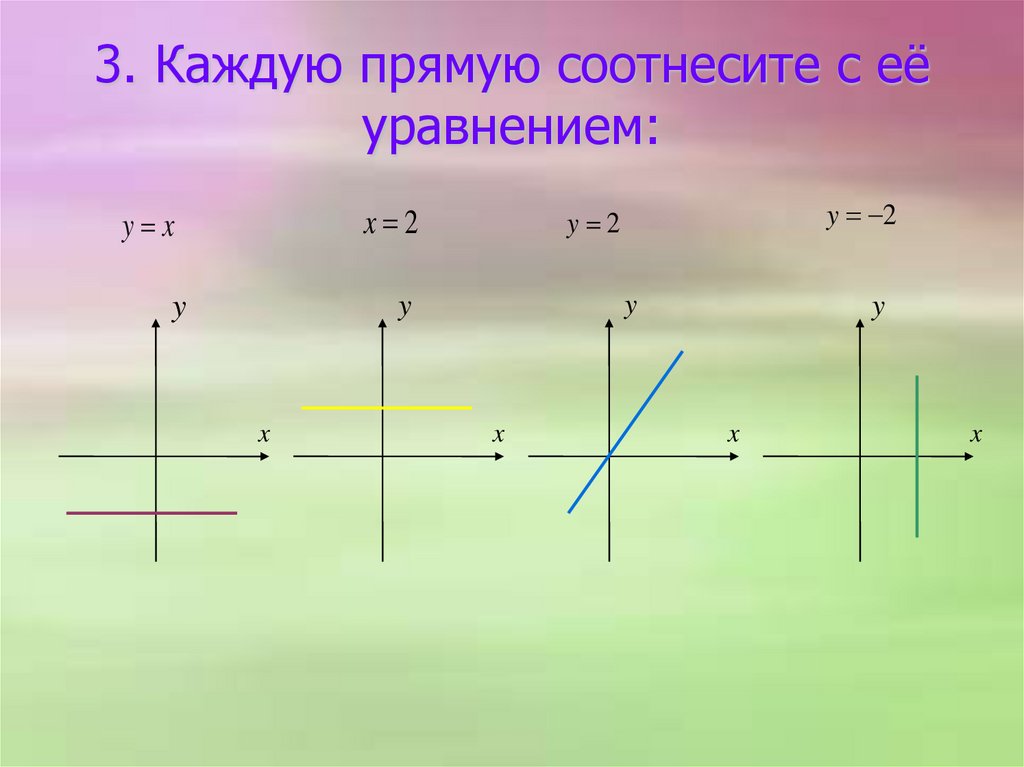
3. Каждую прямую соотнесите с её
уравнением:
x 2
y x
y
y
x
y 2
y 2
y
y
x
x
x

16. 3. Каждую прямую соотнесите с её уравнением:

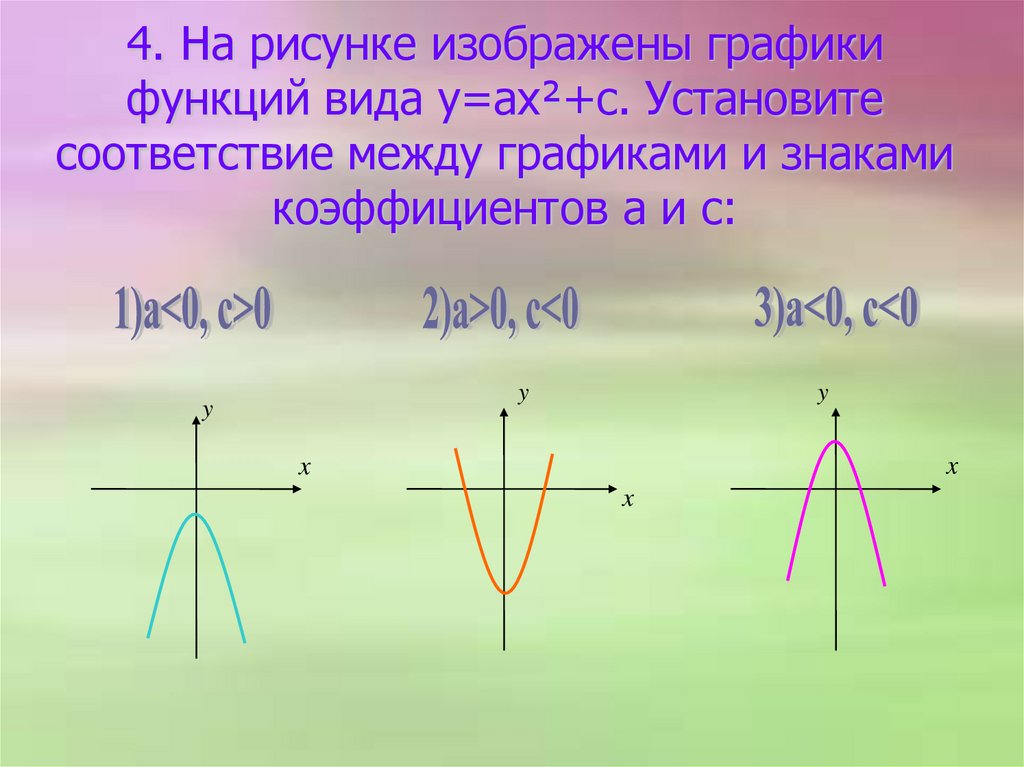
4. На рисунке изображены графики
функций вида y=ax²+с. Установите
соответствие между графиками и знаками
коэффициентов a и c:
y
y
y
x
x
x