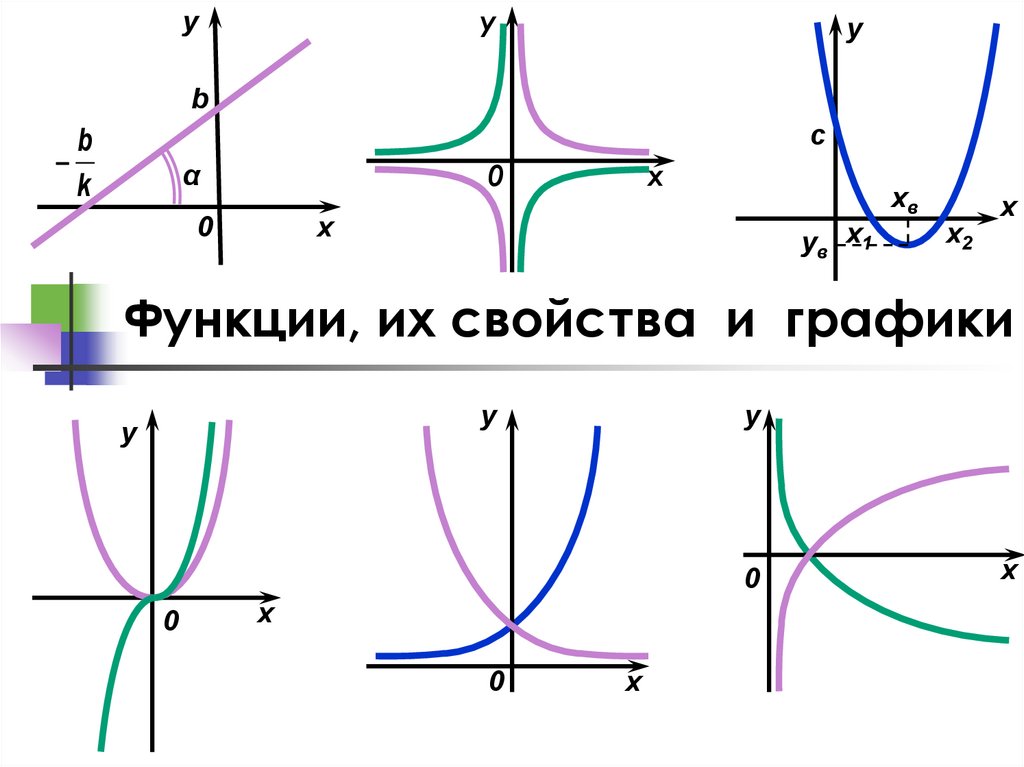
Функции, их свойства и графики

1. Функции, их свойства и графики

y
y
y
b
c
b
k
0
α
0
x
xв
x
ув x1
x
x2
Функции, их свойства и графики
y
y
y
0
0
x
0
x
x

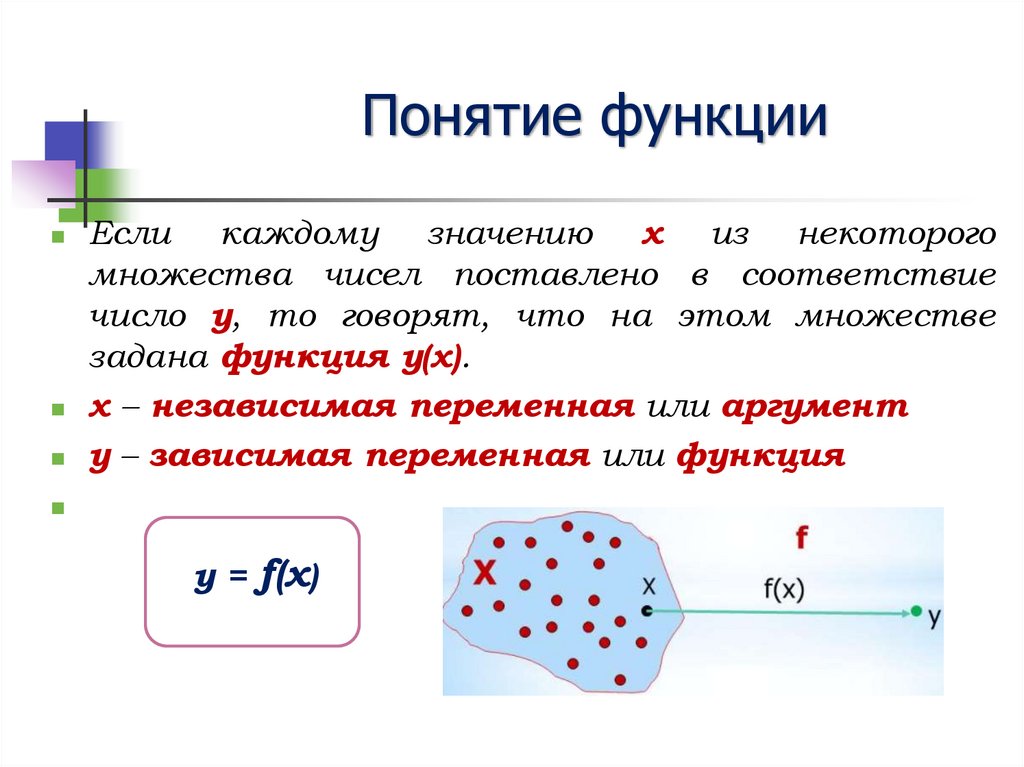
2. Понятие функции

Если каждому значению х из некоторого
множества чисел поставлено в соответствие
число у, то говорят, что на этом множестве
задана функция у(х).
х – независимая переменная или аргумент
у – зависимая переменная или функция
y = f(x)

3.

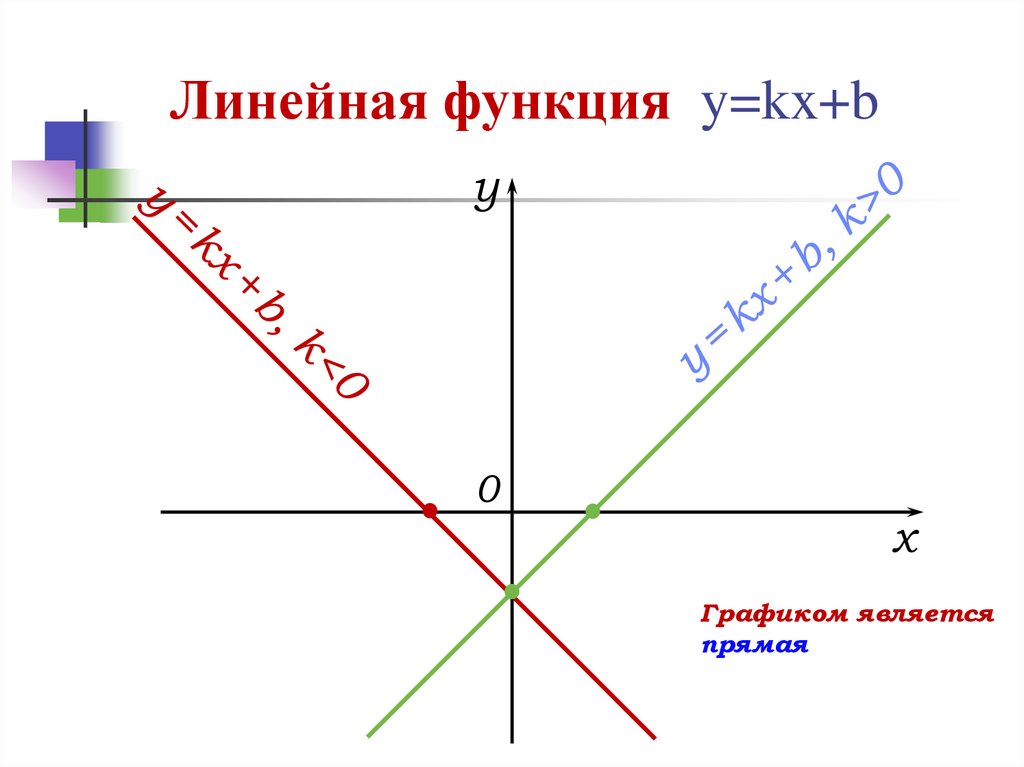
Линейная функция y=kx+b
y
0
x
Графиком является
прямая

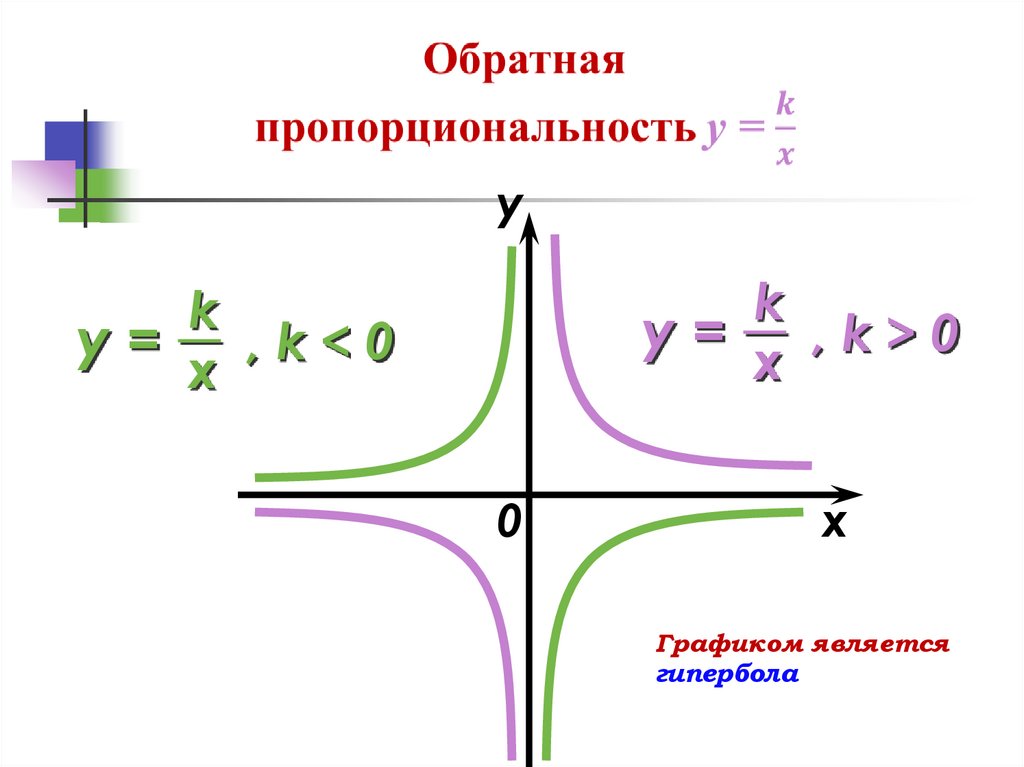
4.

y
k
y=
,k>0
x
k
y=
,k<0
x
0
x
Графиком является
гипербола

5.

Квадратичная функция
y
Графиком является
парабола
c
0 x1
x2
x

6.

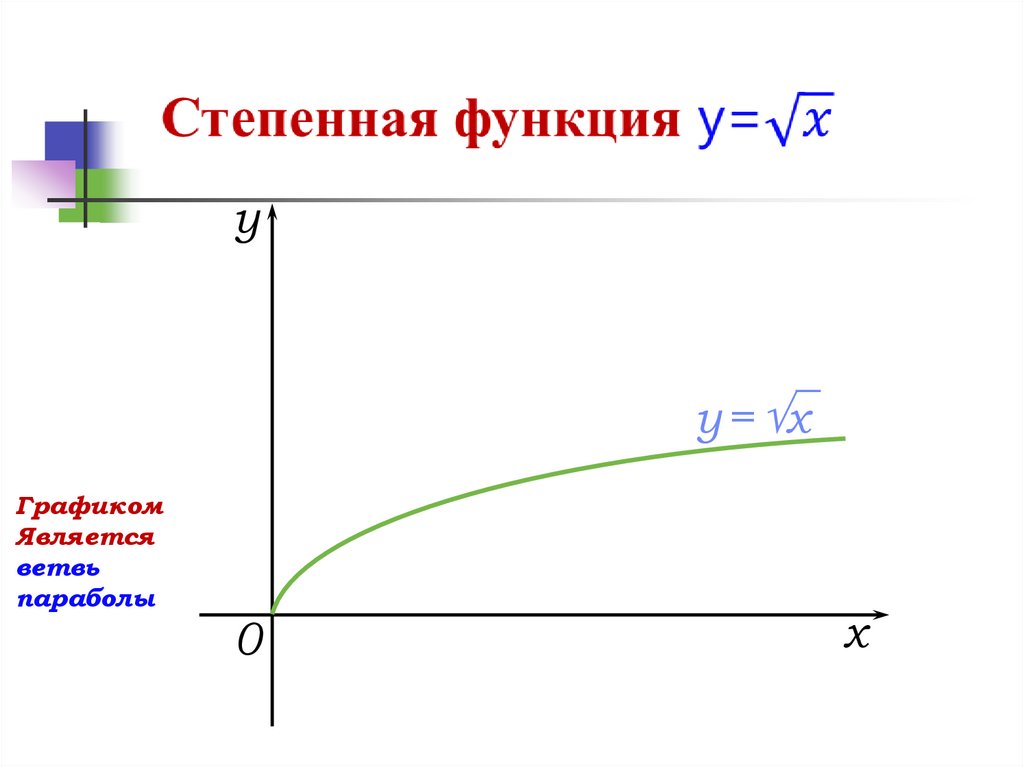
y
y = x
Графиком
Является
ветвь
параболы
0
x

7.

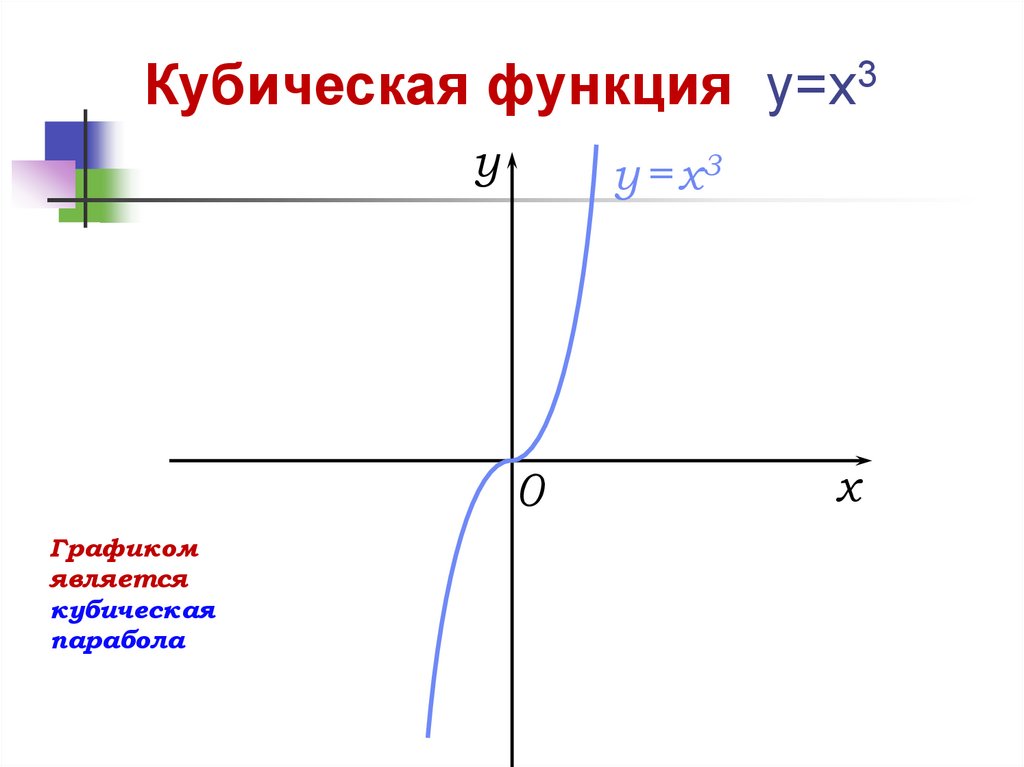
Кубическая функция y=x3
y
y = x3
0
Графиком
является
кубическая
парабола
x

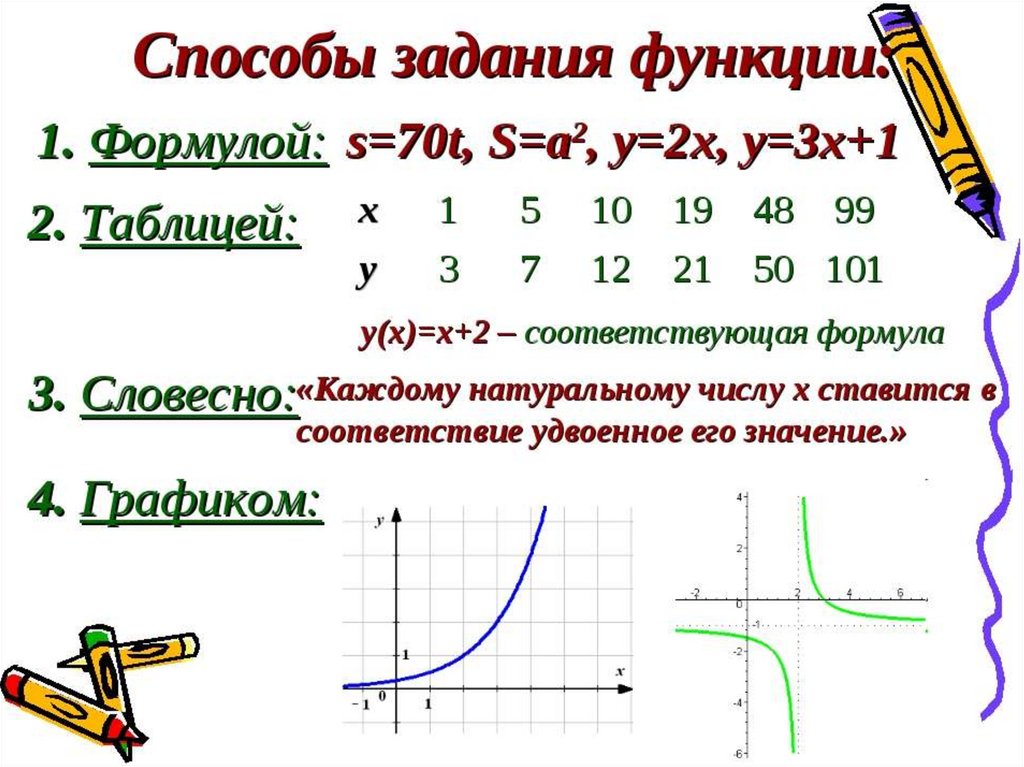
8. Способы задания функции:

9. Свойства функций

10.

11.

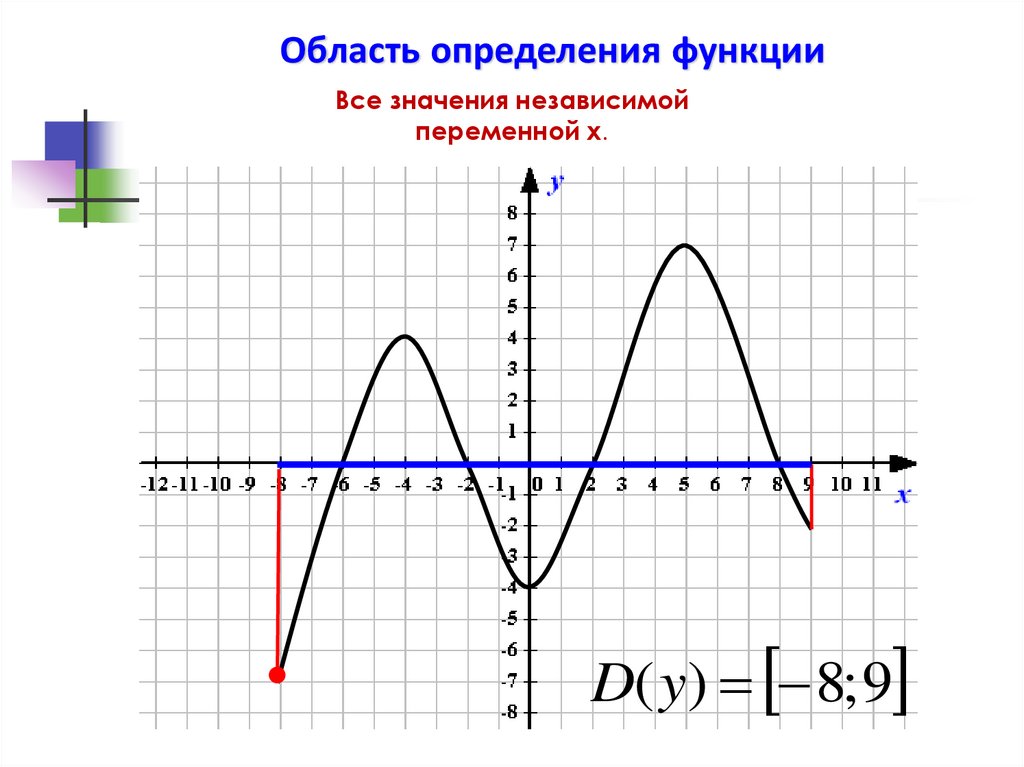
Область определения функции
Все значения независимой
переменной х.
D( y) 8; 9

12.

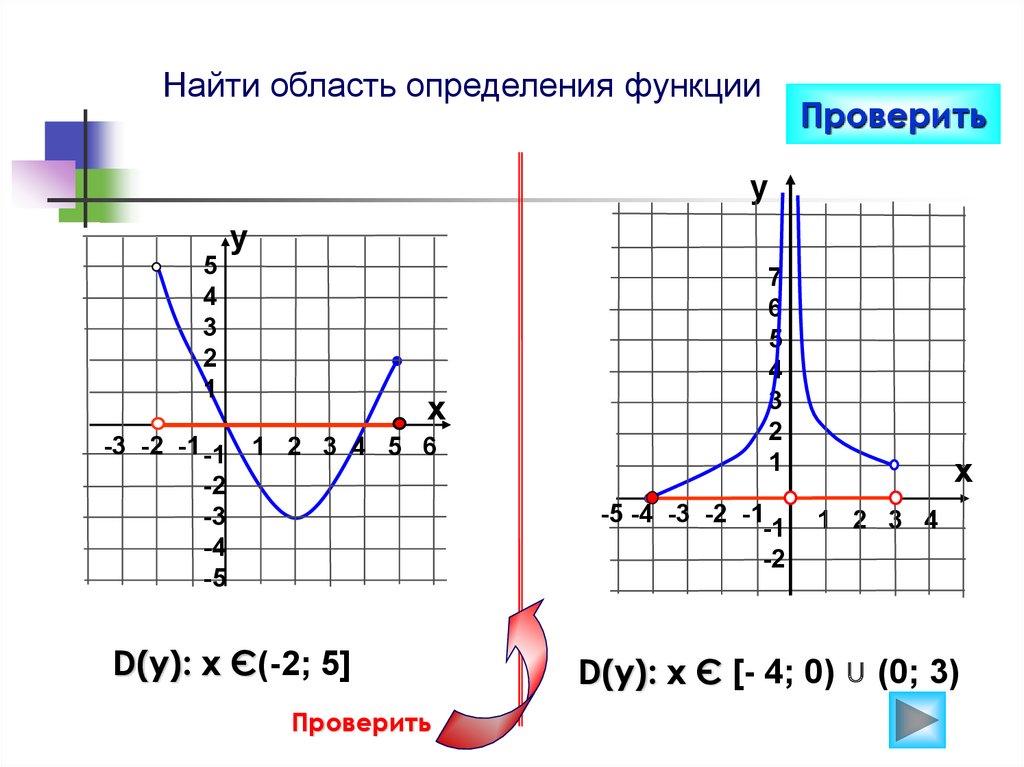
Найти область определения функции
Проверить
у
5
4
3
2
1
у
х
-3 -2 -1 -1 1 2 3 4 5 6
-2
-3
-4
-5
D(y): x Є(-2; 5]
Проверить
7
6
5
4
3
2
1
-5 -4 -3 -2 -1
-1
-2
х
1 2 3 4
D(y): x Є [- 4; 0)
⋃
(0; 3)

13.

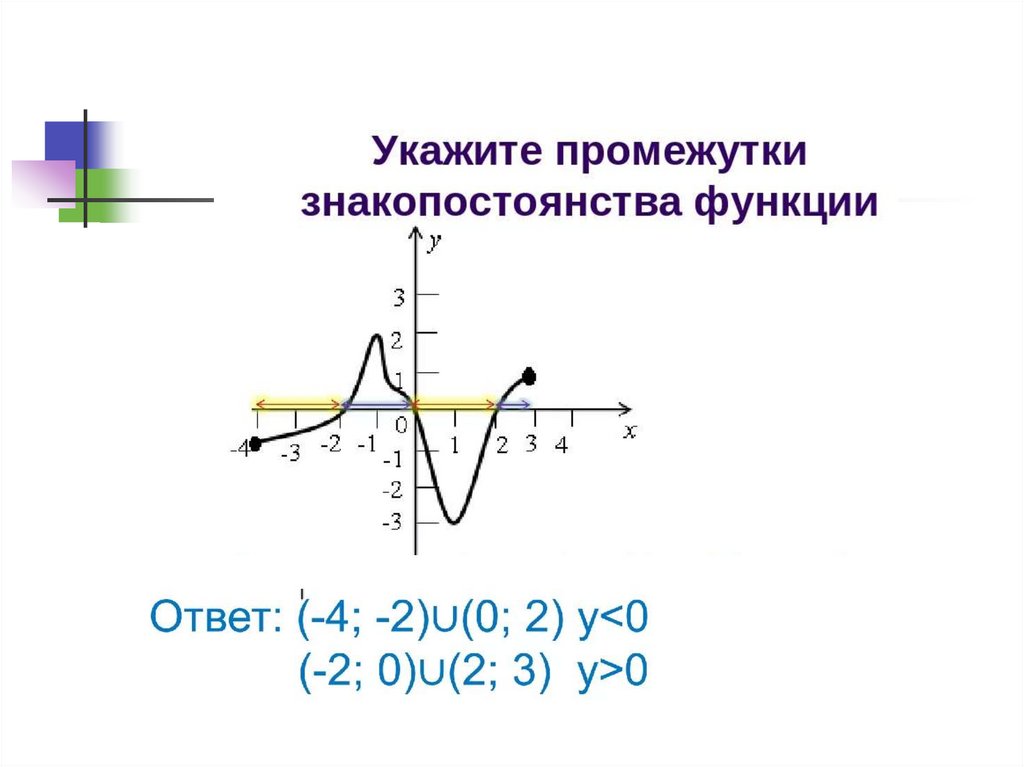
Практическая часть
Проверить
Найти область определения функции
1. у = 3х – 4
Это линейная функция
R
D(y): x
1. у = 6 – 4х2
Это квадратичная функция
R
D(y): x

14.

Найти область определения функции
D(y) = x Є (- ∞; 11)⋃ (11; +∞)

15.

Найти область определения функции
Решение:
Решение:

16.

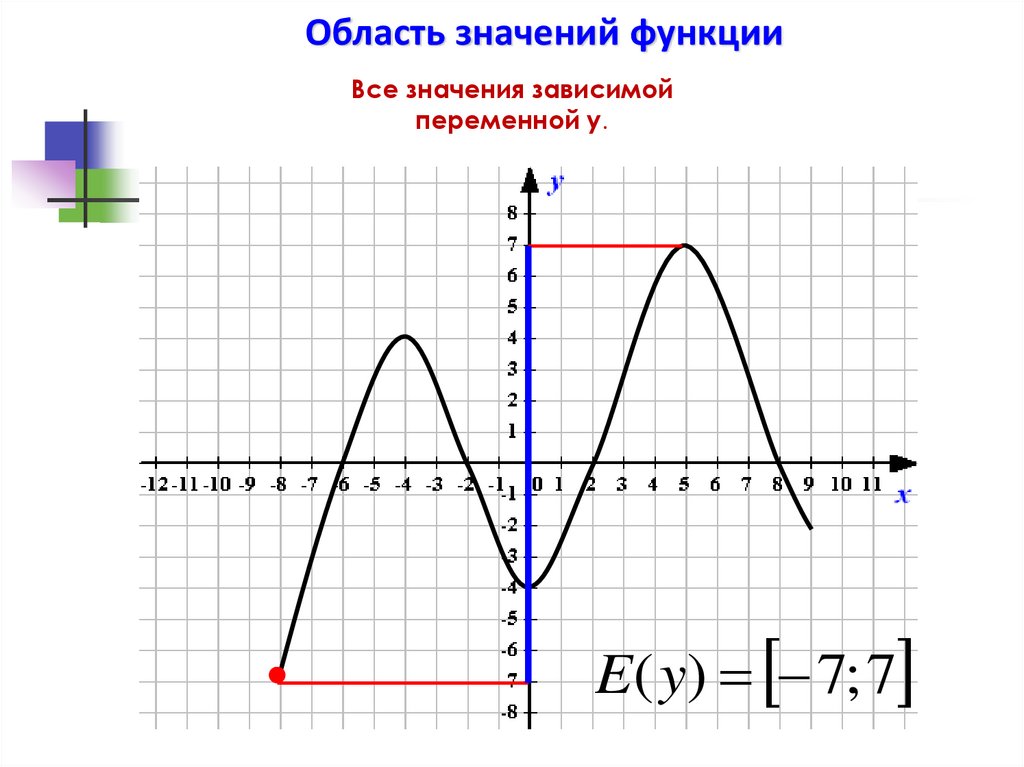
Область значений функции
Все значения зависимой
переменной у.
E( y) 7; 7

17.

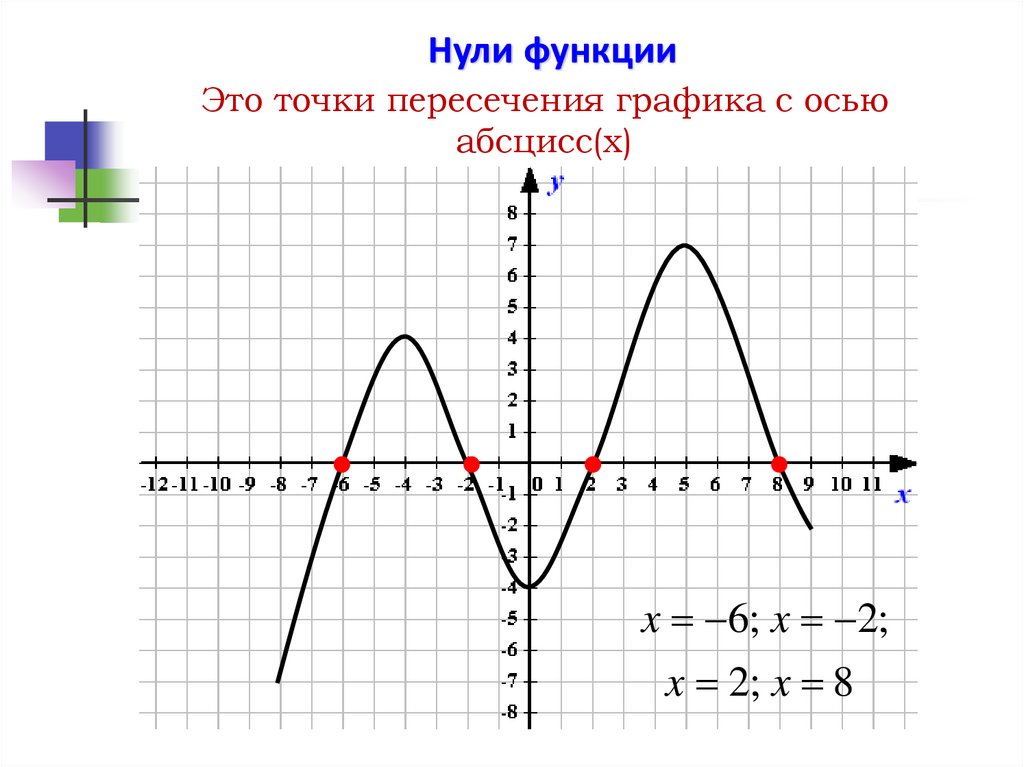
Нули функции
Это точки пересечения графика с осью
абсцисс(х)
x 6; x 2;
x 2; x 8

18.

19.

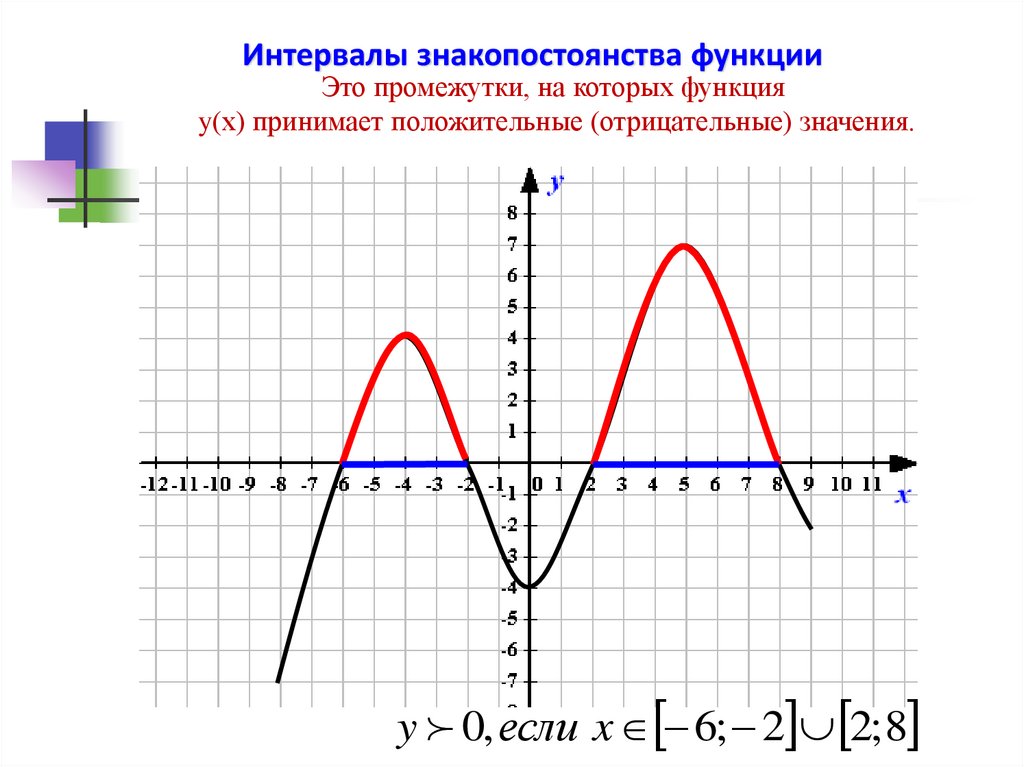
Интервалы знакопостоянства функции
Это промежутки, на которых функция
y(х) принимает положительные (отрицательные) значения.
y 0, если x 6; 2 2; 8

20.

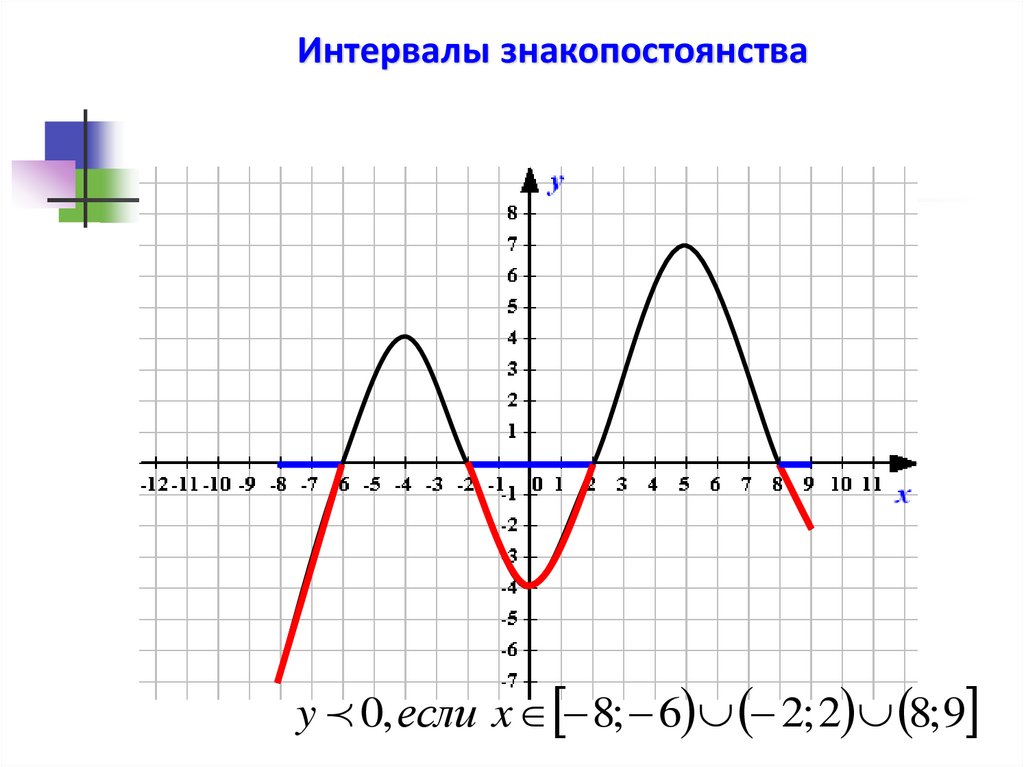
Интервалы знакопостоянства
y 0, если x 8; 6 2; 2 8; 9

21.

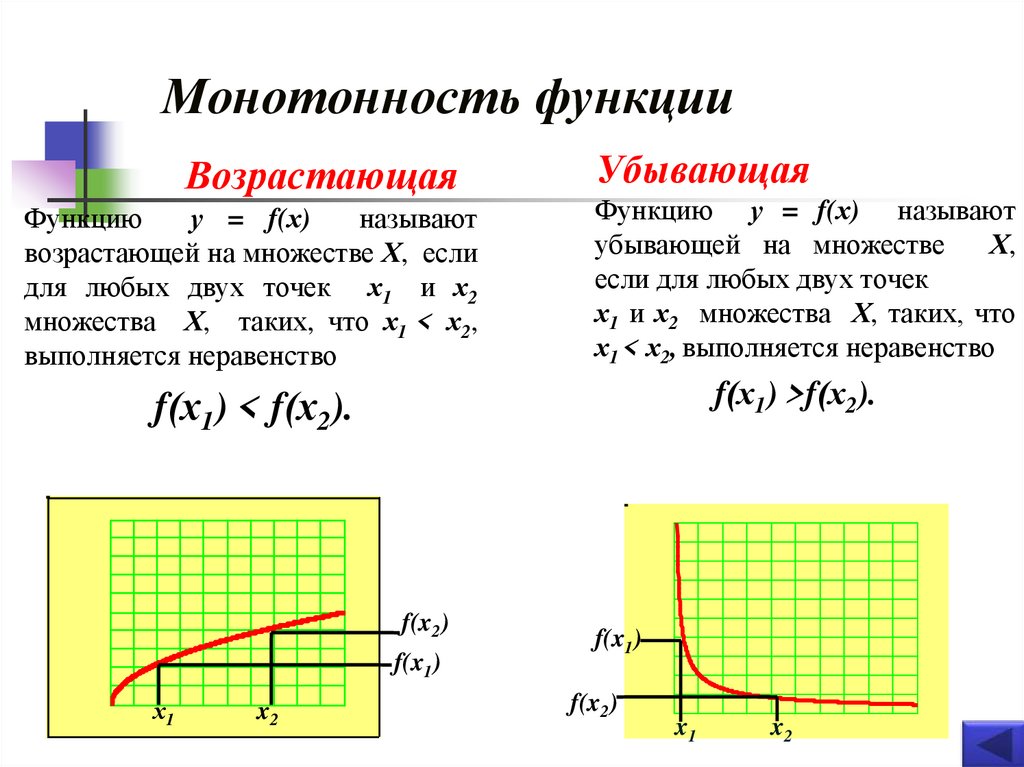
22. Монотонность функции

Возрастающая
Функцию
у = f(х)
называют
возрастающей на множестве Х, если
для любых двух точек х1 и х2
множества Х, таких, что х1 < х2,
выполняется неравенство
Убывающая
Функцию у = f(х) называют
убывающей на множестве
Х,
если для любых двух точек
х1 и х2 множества Х, таких, что
х1 < х2, выполняется неравенство
f(х1) >f(х2).
f(х1) < f(х2).
f(x2)
f(x1)
х1
x2
f(x1)
f(x2)
x1
x2

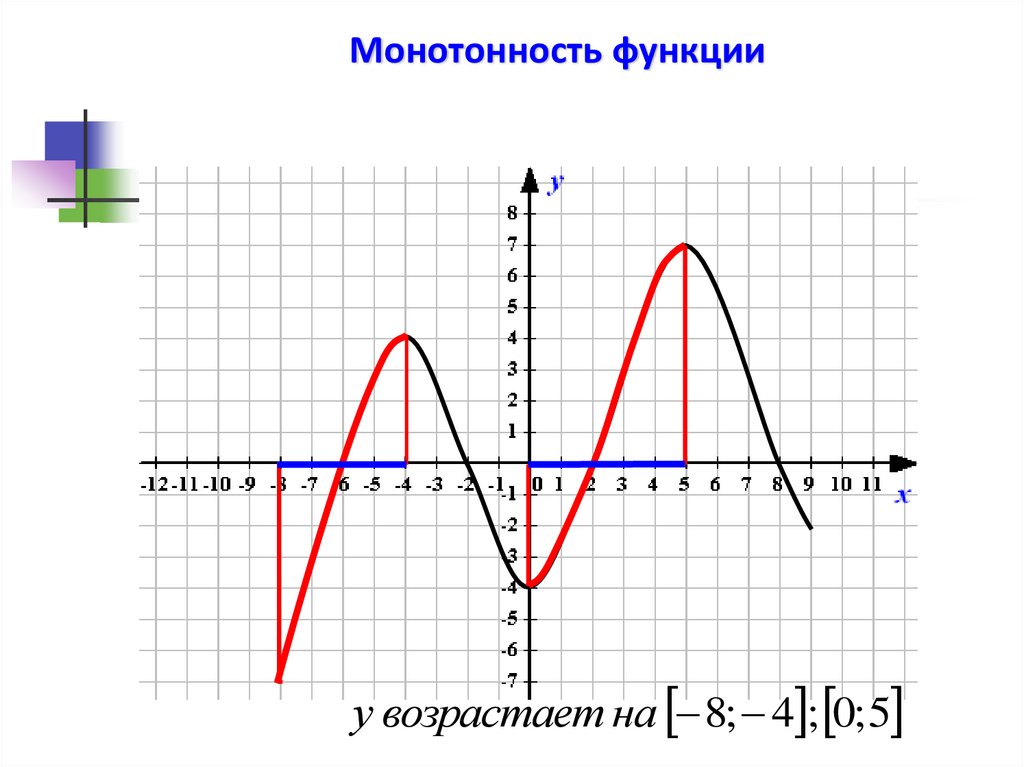
23.

Монотонность функции
у возрастает на 8; 4 ; 0; 5

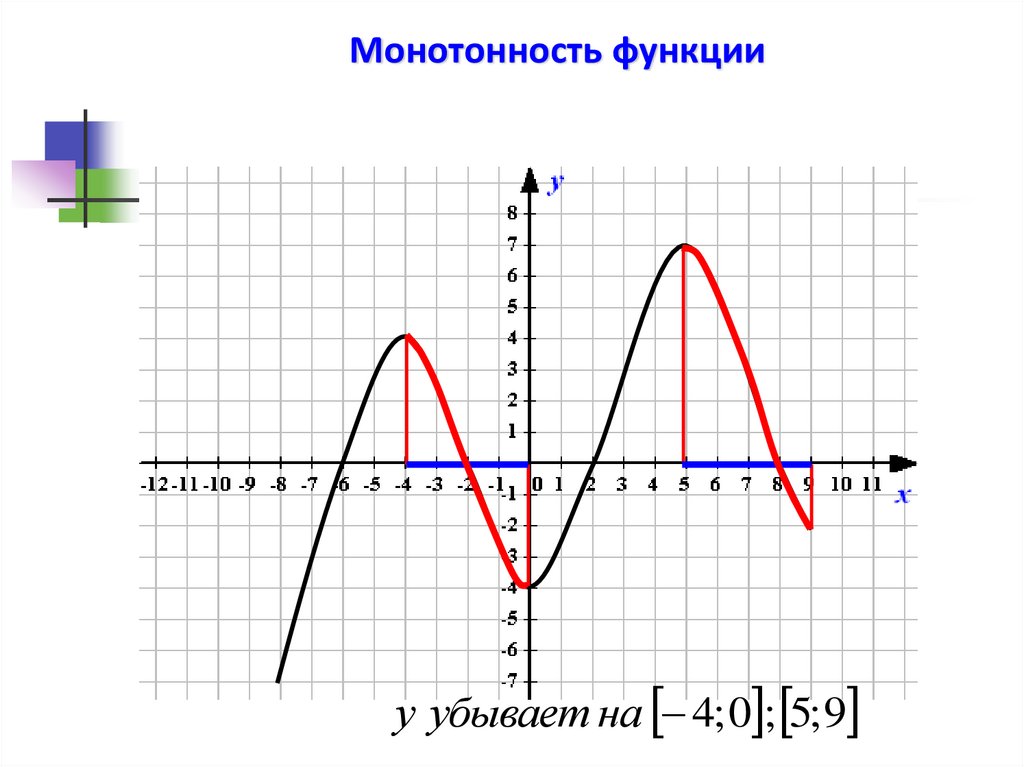
24.

Монотонность функции
у убывает на 4; 0 ; 5; 9

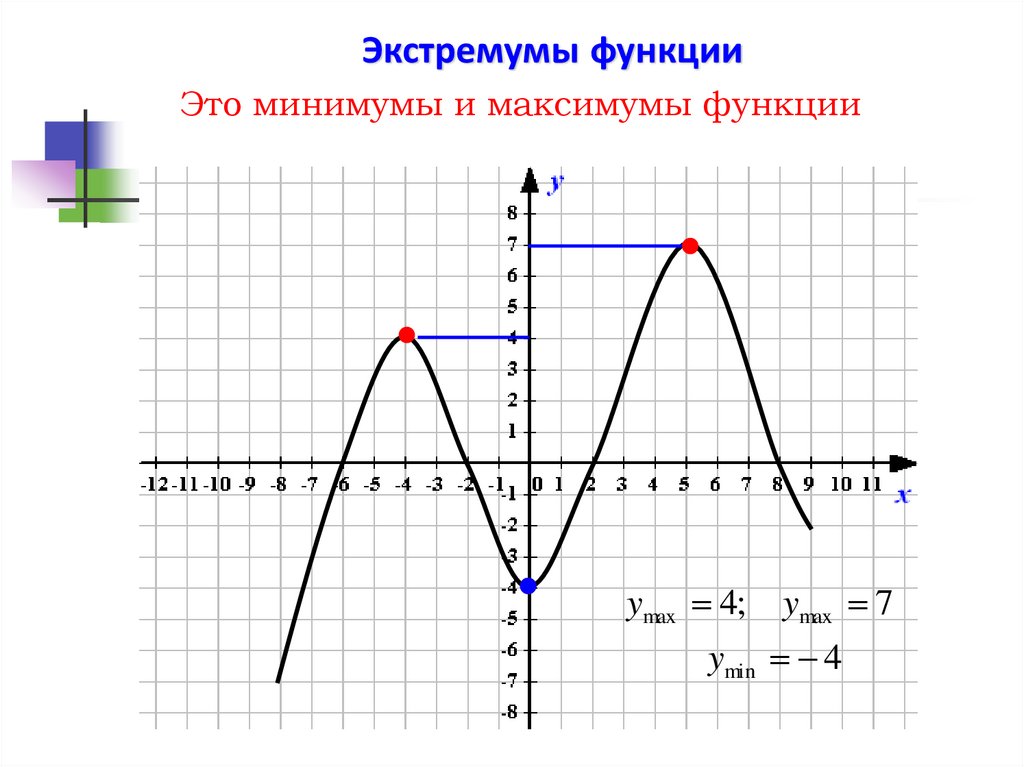
25.

Экстремумы функции
Это минимумы и максимумы функции
ymax 4;
ymax 7
ymin 4

26.

Точки экстремума функции
xmax 4; xmax 5
xmin 0

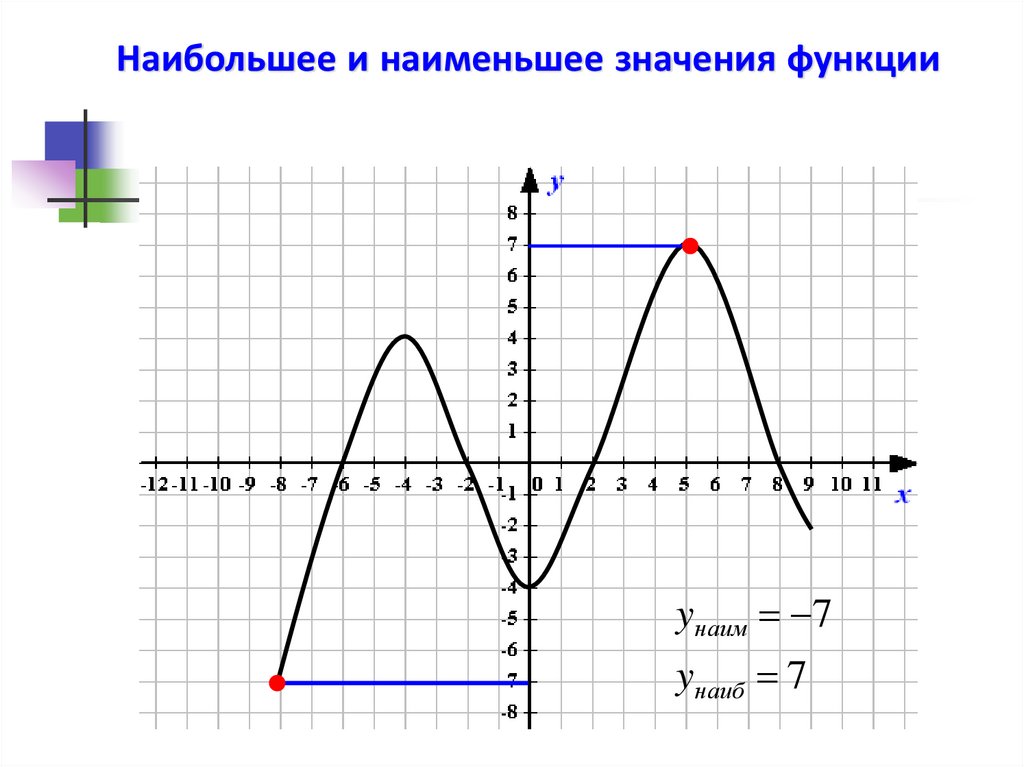
27.

Наибольшее и наименьшее значения функции
yнаим 7
yнаиб 7