Уравнение tgx = a

1.

tgx = a

2. Арктангенс.

а
у
π/2
arctg а = t
0
х
arctg(- а )
-π/2
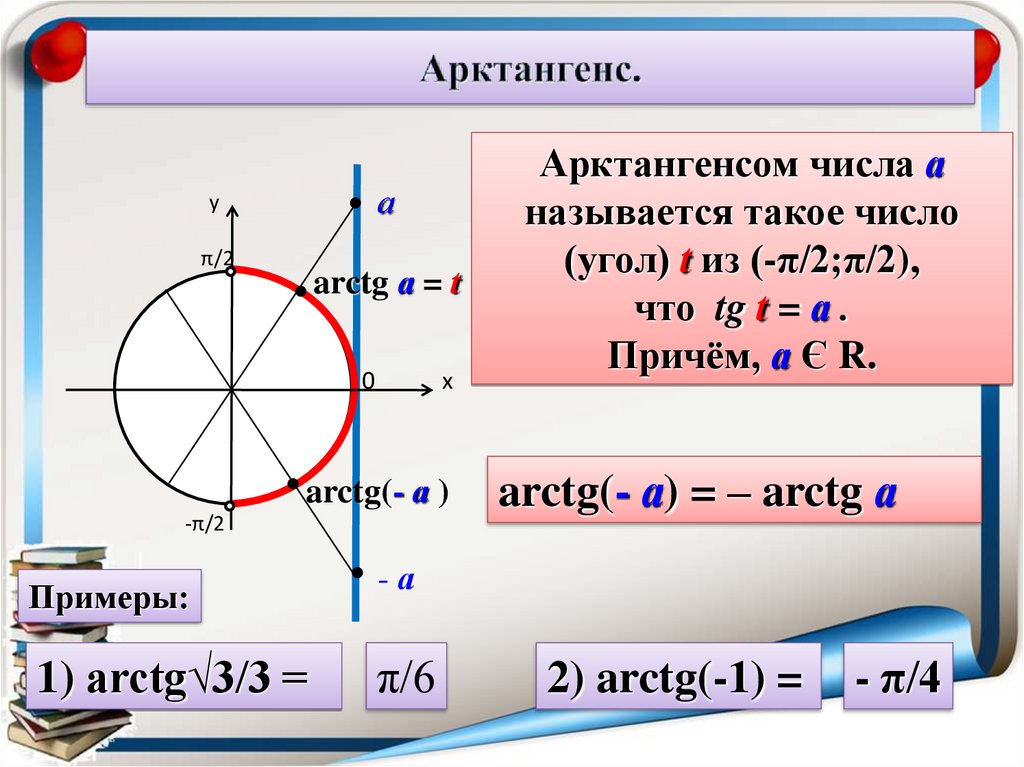
Примеры:
1) arctg√3/3 =
Арктангенсом числа а
называется такое число
(угол) t из (-π/2;π/2),
что tg t = а .
Причём, а Є R.
arctg(- а) = – arctg а
-а
π/6
2) arctg(-1) =
- π/4

3. АРКТАНГЕНС ЧИСЛА

Например
3
arctg
;
6
3
arctg 0 0;
arctg1 ;
4
т.к.
т.к.
т.к.
3
; tg
.
2 6 2
6
3
2
2
0
4
2
2
; tg 0 0.
; tg
4
1.

4. АРКТАНГЕНС ЧИСЛА Основные формулы

1
3
2arctg1 3arctg
2 3arctg
3
4
3
3 0
2
6 2 2
2 3
1
6 4
2. 6arctg 3 4 arcsin
3
4
2
1.
3.
3
3 3 2
2 arccos
3arctg
6
6
3
2
7
5
2
6
2
6

5.

Уравнение tgx = a
Из определения тангенса следует, что tg x может
принимать любое действительное значение.
Поэтому уравнение tg x = a имеет корни при любом
значении.
а ;

6.

Решить уравнение tgx = 1
у
1
1
4
0
4
0
х
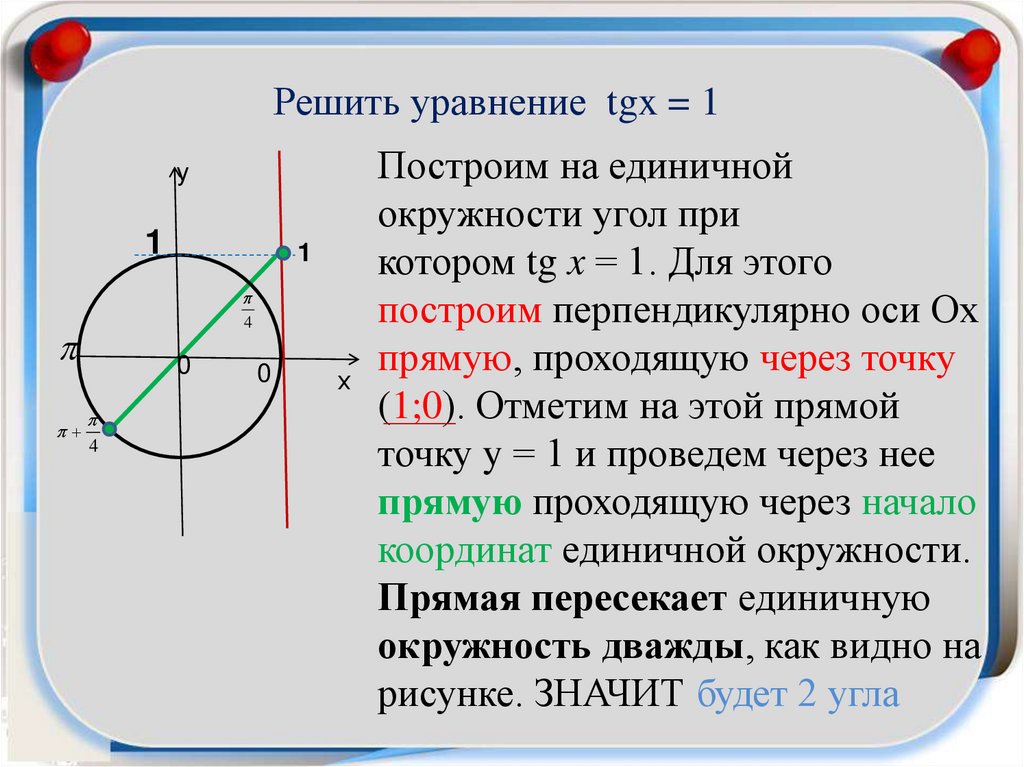
Построим на единичной
окружности угол при
котором tg x = 1. Для этого
построим перпендикулярно оси Ох
прямую, проходящую через точку
(1;0). Отметим на этой прямой
точку y = 1 и проведем через нее
прямую проходящую через начало
координат единичной окружности.
Прямая пересекает единичную
окружность дважды, как видно на
рисунке. ЗНАЧИТ будет 2 угла

7.

х1
4
2 k , k Z
х2
4
2 k , k Z
Объединим эти два ответ в один заметив, что точки
повторяются через π
х
Ответ
х
4
4
n, n Z
n, n Z
Если а≥0, то корень уравнения заключен в промежутке
0; 2 ;
Если а<0, то корень уравнения заключен в промежутке
;0 ;
2

8.

Общее решение уравнения tg x = a
tgx a, a R x arctga k , k Z .
tgx a, a R x arctga k , k Z .

9.

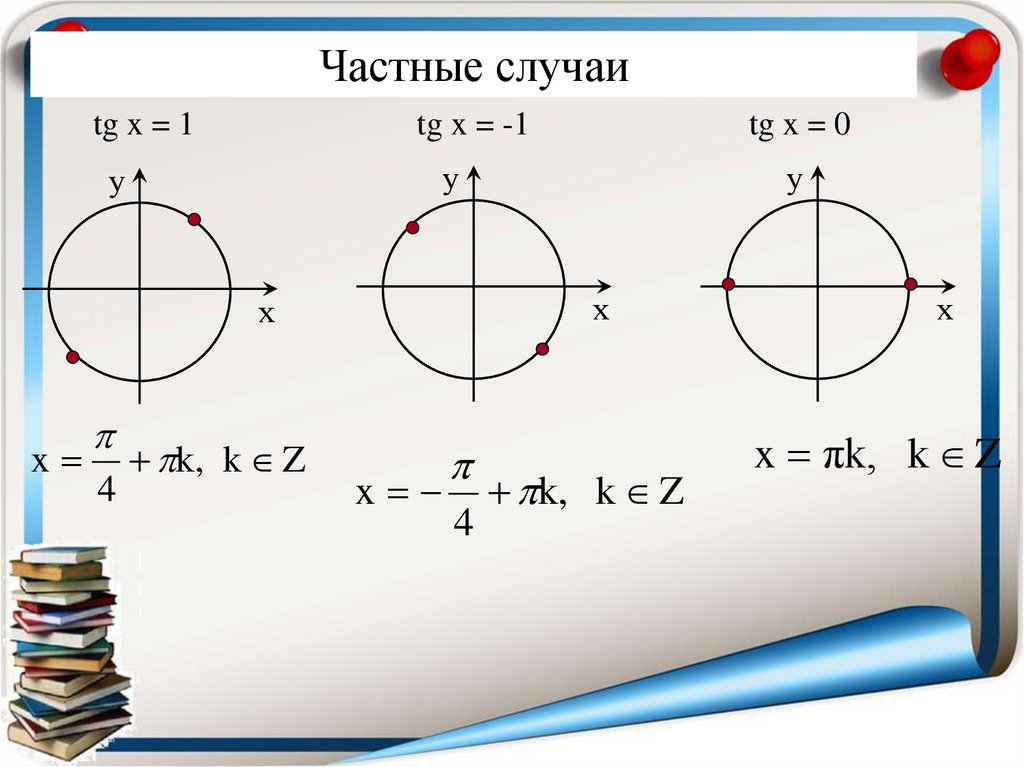
Частные случаи
tg x = 1
tg x = -1
у
у
x
4
k, k Z
у
х
х
tg x = 0
x
4
k, k Z
х
x πk, k Z

10. Тренируемся решать:

tg2x = -1
2x = arctg (-1) + πk, kЄZ
2x = -π/4 + πk, kЄZ
x = -π/8 + πk/2, kЄZ
Ответ: -π/8 + πk/2, kЄZ.

11. Тренируемся решать:

tg x
0
4
x
4
x
4
n, n
n, n
Ответ :
4
n, n

12. Уравнение tgx=a

Пример 1.
3
tgx
3
3
x arctg
k
3
x k , k Z .
Пример 2.
tg 2 x 4
2 x arctg 4 k
1
k
x arctg 4 , k Z .
2
2
6
Ответ:
6
k , k Z .
1
k
Ответ: 2 arctg 4 2 , k Z .

13.

Тренируемся решать:
Решить уравнение:
3tgx- 3= 0
3tgx= 3 |:3.
tgx= 1
x
4
k , k Z
Ответ:
4
k , k Z

14.

Решить уравнение tgx = 2
х arctga n, n Z
х arctg 2 n, n Z
ответ
arctg 2 n, n Z
Решить уравнение tgx = -4
х arctg ( 4) n, n Z
ответ х arctg 4 n, n Z

15. Уравнение tgx=a

Пример 3.
tg 2 x 3;
4
2x
4
3
k ;
7
2 x k ;
12
Ответ:
3
ctg 2 x
4 3
2x
4
2x
arctg 3 k ;
3
4
k ;
7
k
x , k Z.
24
2
7
k
, k Z.
24
2

16.

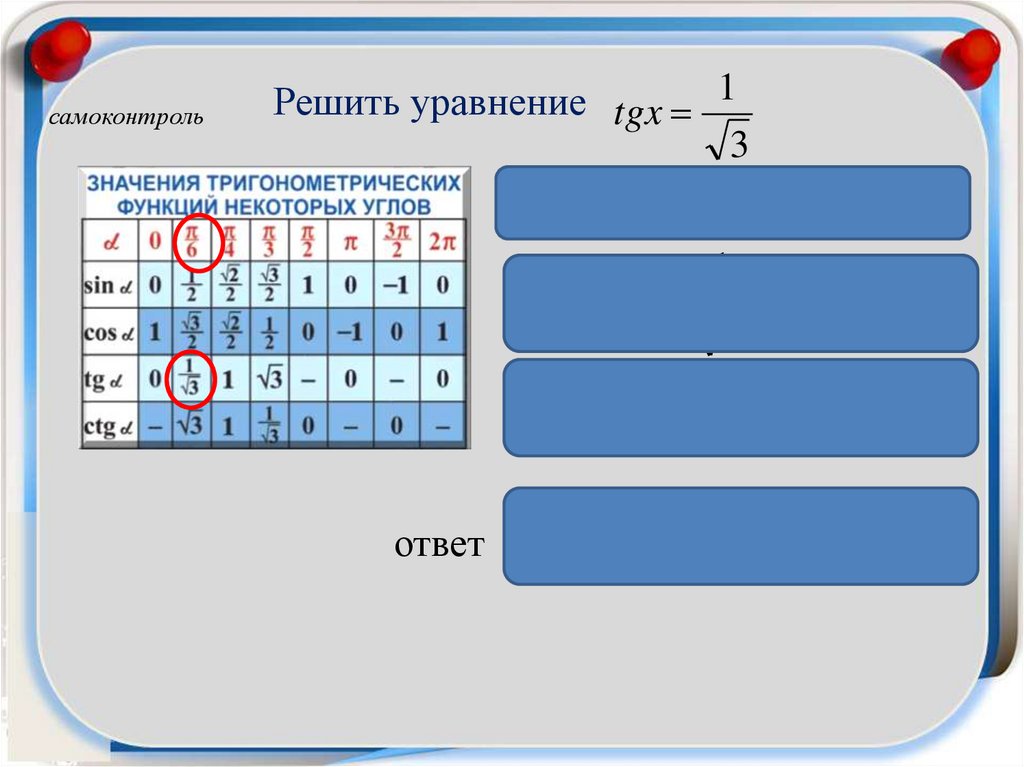
самоконтроль
Решить уравнение tgx 1
3
х arctga n, n Z
1
х arctg
n, n Z
3
х n, n Z
6
ответ х n, n Z
6

17.

Решить уравнение
х
3 tg 0
6
х arctga n, n Z
х
arctg ( 3 ) n, n Z
6
arctg ( a) arctga
ответ
х 2 6 n, n Z
х Проверить решение
arctg 3 n, n Z
6
х
n, n Z
6
3
6
х
6 n, n Z
3

18.

Решить уравнение tg 2 x 3
2 х arctg ( 3 ) n, n Z
2 x arctg 3 n
Проверить
2 x n решение
3
x
ответ
x
6
n
2
6
,n Z
n
2
,n Z

19.

Решить уравнение:
tg(π/3- х)= √3
- tg(х-π/3)= √3
3x- π/3=arctg(√3)+ πk, к є Z
3x- π/3= π/3+ πk, к є Z
3x=2π/3 + πk, к є Z
x=2π/9 + πk/3 , к є Z
Ответ: 2π/9 + πk/3, к є Z .