Похожие презентации:
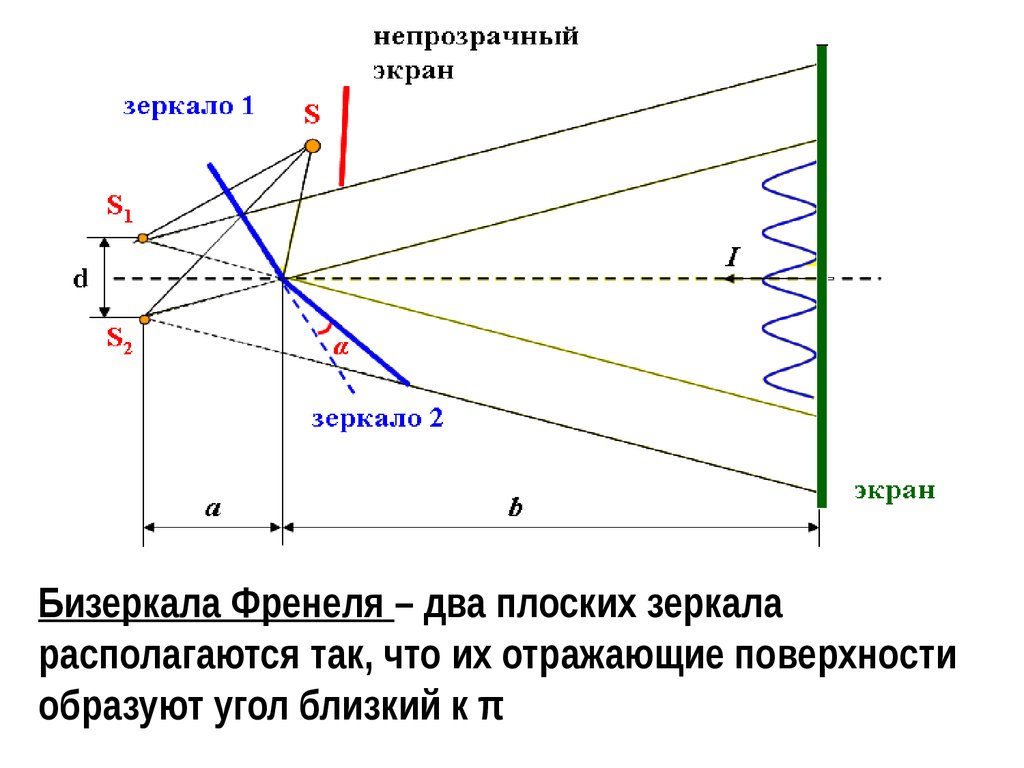
Бизеркала Френеля
1.
2.
23.
Бизеркала Френеля – два плоских зеркаларасполагаются так, что их отражающие поверхности
образуют угол близкий к π
4.
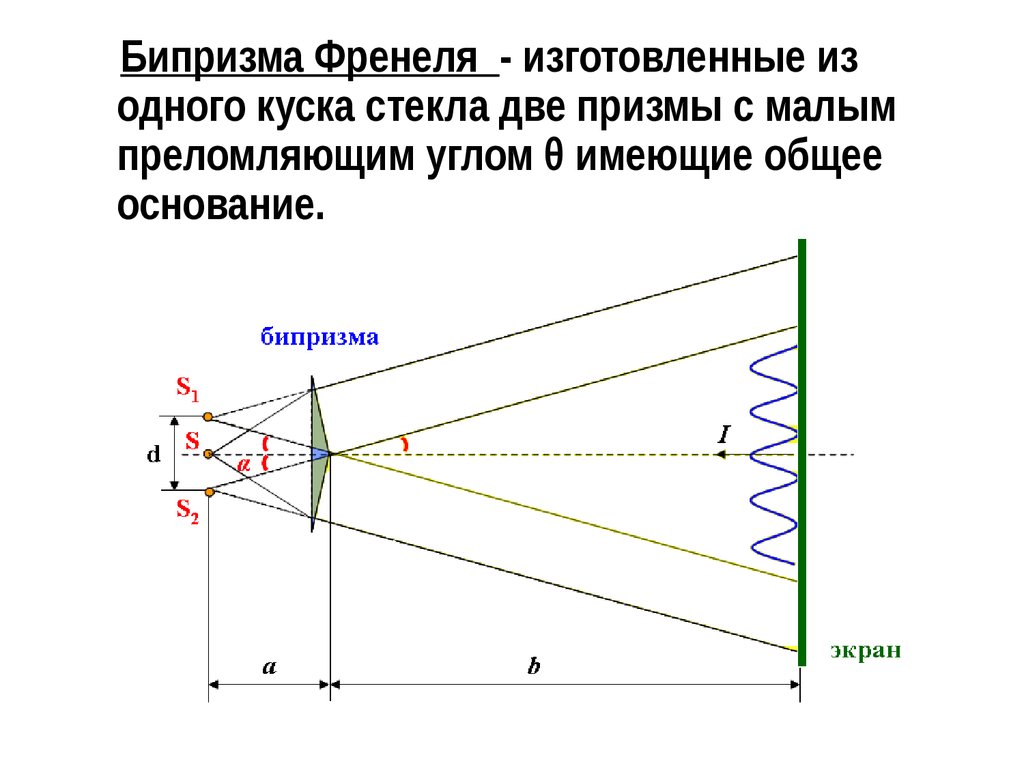
Бипризма Френеля - изготовленные изодного куска стекла две призмы с малым
преломляющим углом θ имеющие общее
основание.
5.
Кольца Ньютона6.
Rl0r=
(m - 1)
2
( m = 1, 2,3....)
где R – радиус плосковыпуклой линзы.
Четным m соответствуют радиусы светлых
колец, нечетным радиусы темных колец
(наблюдение в отраженном свете).
В проходящем свете – наоборот.
7.
Полосы равной толщиныПолосы на
поверхности
клина с углом
наклона меньшим
или равным
нескольким
угловым минутам
Кольца Ньютона
8.
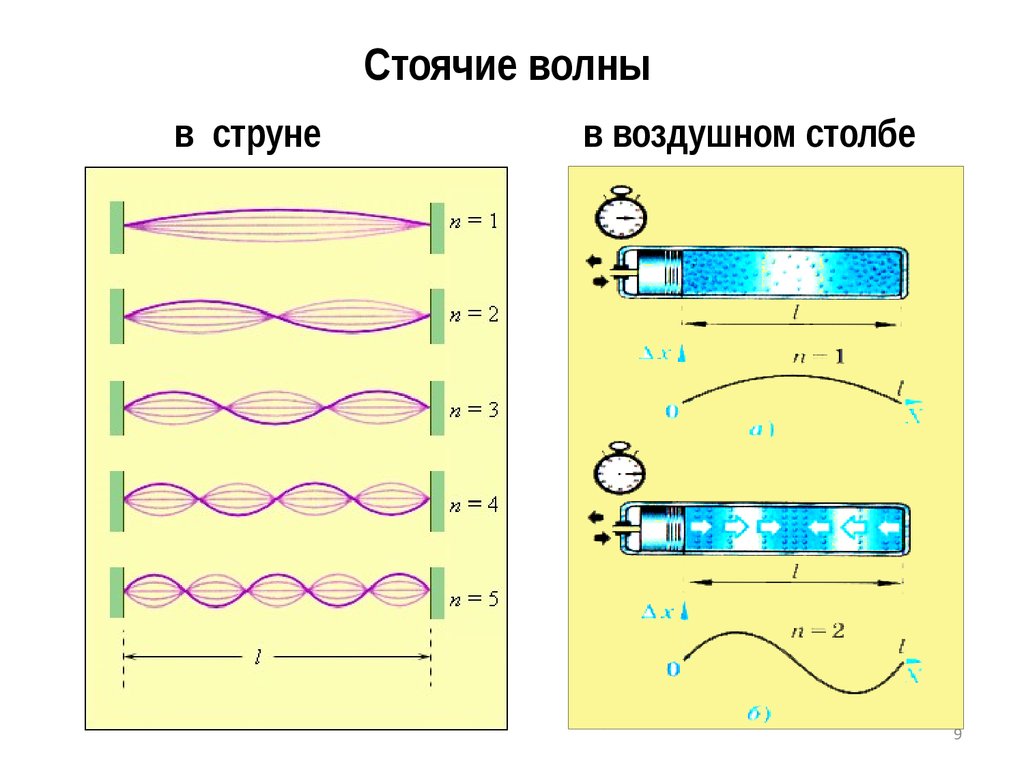
Стоячие волны.
Стоячие волны образуются в результате
интерференции двух встречных плоских волн
(например, бегущей и отраженной волны).
= A cos ( t - kx )
1
2 = A cos( t kx )
8
9.
Стоячие волныв струне
в воздушном столбе
9
10.
..
При интерференции встречных волн 1 и 2
образуется результирующая волна:
( x, t ) = = 2 A cos kx cos t
1
2
2
2
Если разность фаз
= 0, то
( x, t ) = = 2 A cos ( kx ) cos ( t )
Если
= , то
1
2
разность
фаз
( x, t ) = = 2 A sin ( kx ) sin ( t )
1
2
10
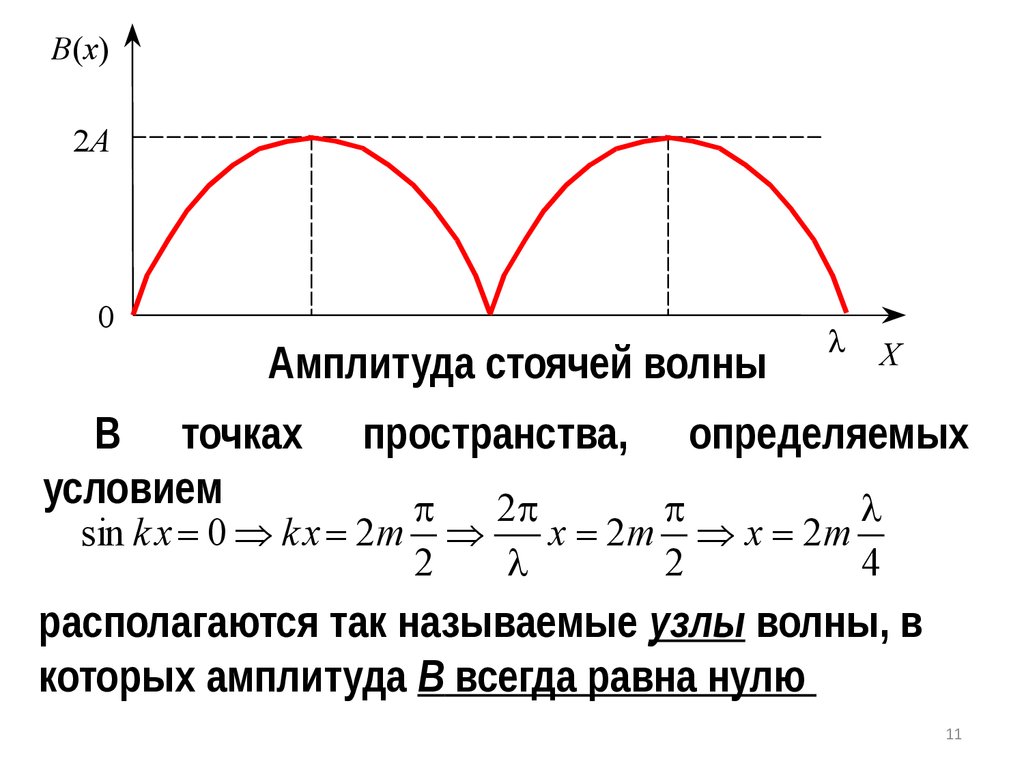
11.
B(x)2A
0
Амплитуда стоячей волны
В точках
условием
пространства,
l X
определяемых
2
l
sin k x = 0 k x = 2m
x = 2m x = 2m
2
l
2
4
располагаются так называемые узлы волны, в
которых амплитуда В всегда равна нулю
11
12.
В точкахусловием
пространства,
определяемых
2
l
sin kx = 1 kx = ( 2m 1) x = ( 2m 1) x = ( 2m 1)
2 l
2
4
.
располагаются так называемые пучности
волны, в которых амплитуда В может быть
максимальной, то есть В = 2А, в моменты
времени, определяемые условием
2
T
sin t = 1 t = ( 2m 1) t = ( 2m 1) t = ( 2m 1)
2
T
2
4
12
13.
В остальных точках пространства амплитудаволны может изменяться в пределах:
0 < B < 2A.
Образовавшаяся в результате интерференции
волна является стоячей – через узлы энергия
не переносится.
13
14.
Стоячие волны в ограниченных средахКраевые условия:
•в точках закрепления струны или стержня, а
также на заглушках труб, всегда возникают
узлы стоячей волны (в этих местах волна
отражается от более плотной среды);
•на свободных концах стержня и на открытых
концах труб всегда возникают пучности
стоячей волны (в этих местах волна
отражается от менее плотной среды).
14
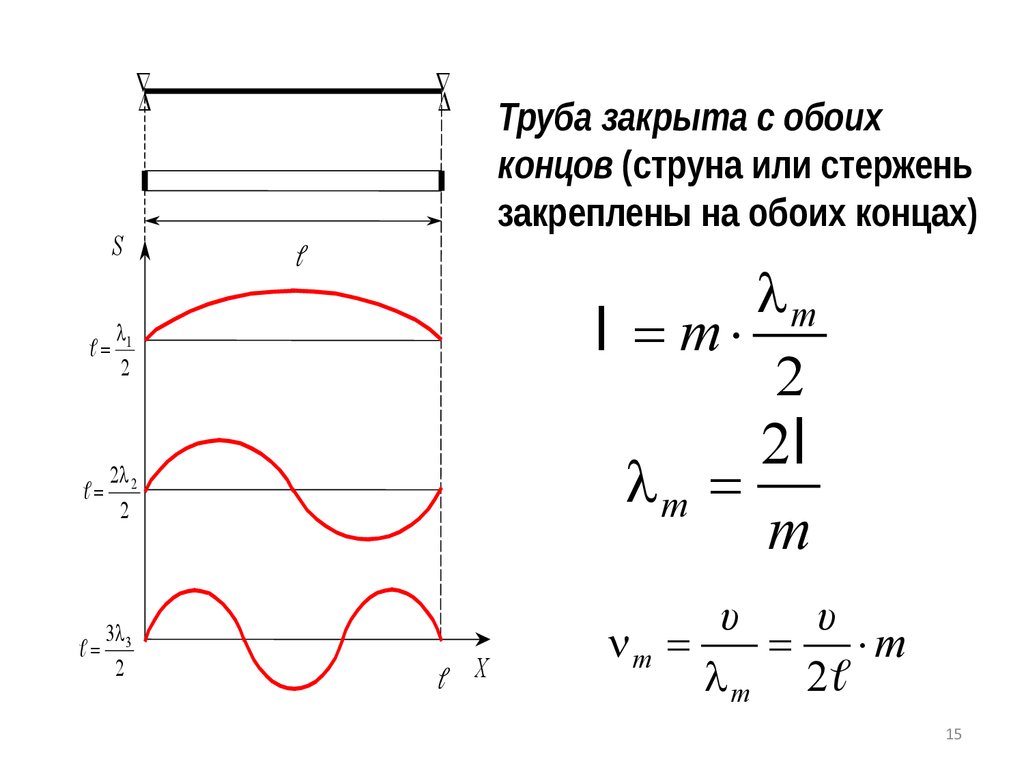
15.
S=
=
lm
l = m
2
2l
lm =
m
l1
2
2l 2
2
3l
= 3
2
Труба закрыта с обоих
концов (струна или стержень
закреплены на обоих концах)
X
υ
υ
m =
= m
l m 2
15
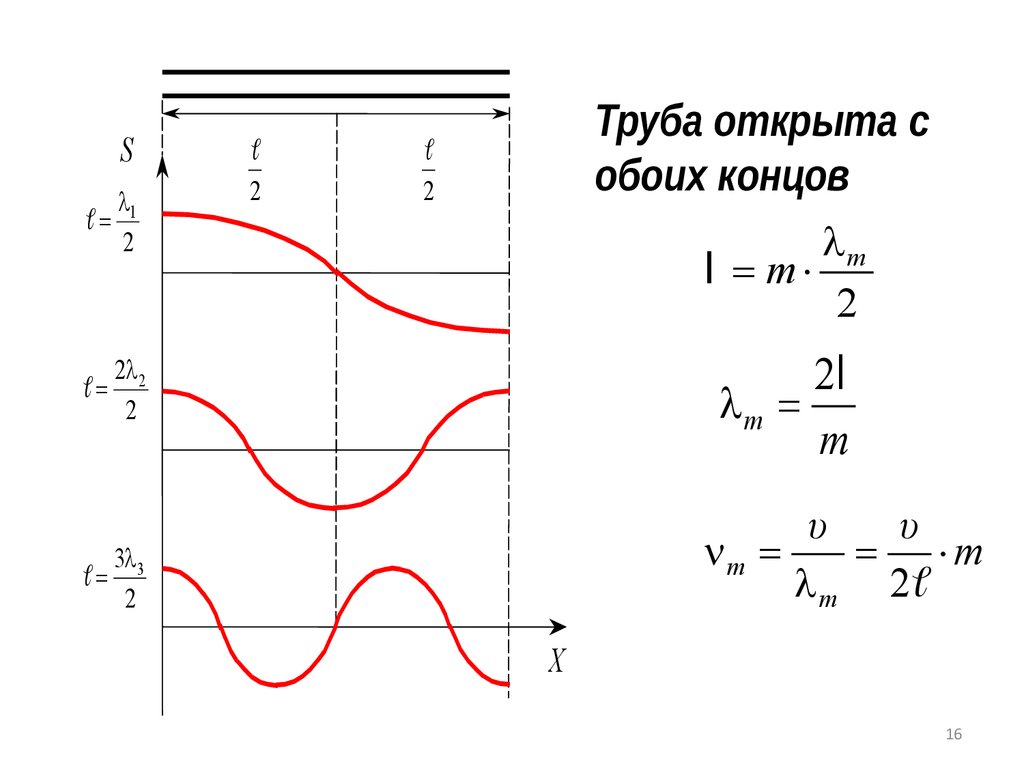
16.
S=
l1
2
=
2l 2
2
=
2
Труба открыта с
обоих концов
2
lm
l = m
2
2l
lm =
m
υ
υ
m =
= m
l m 2
3l 3
2
X
16
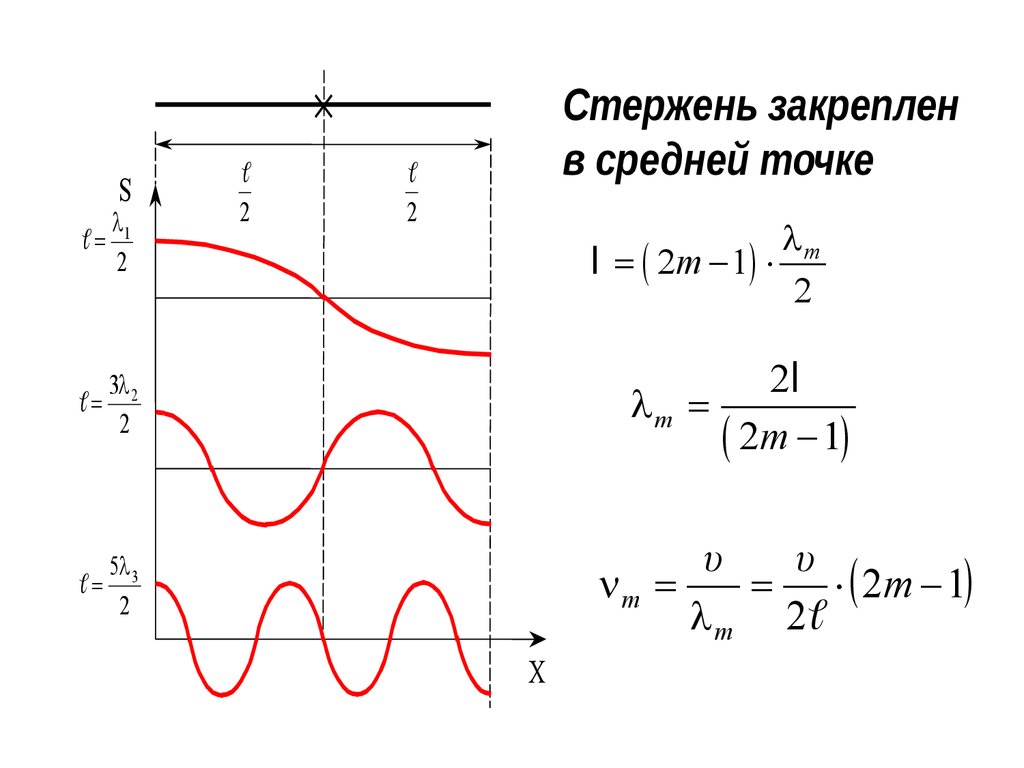
17.
S=
l1
2
2
Стержень закреплен
в средней точке
2
lm
l = ( 2m - 1)
2
2l
lm =
( 2m - 1)
3l
= 2
2
υ
υ
m =
= ( 2m - 1)
l m 2
5l
= 3
2
X
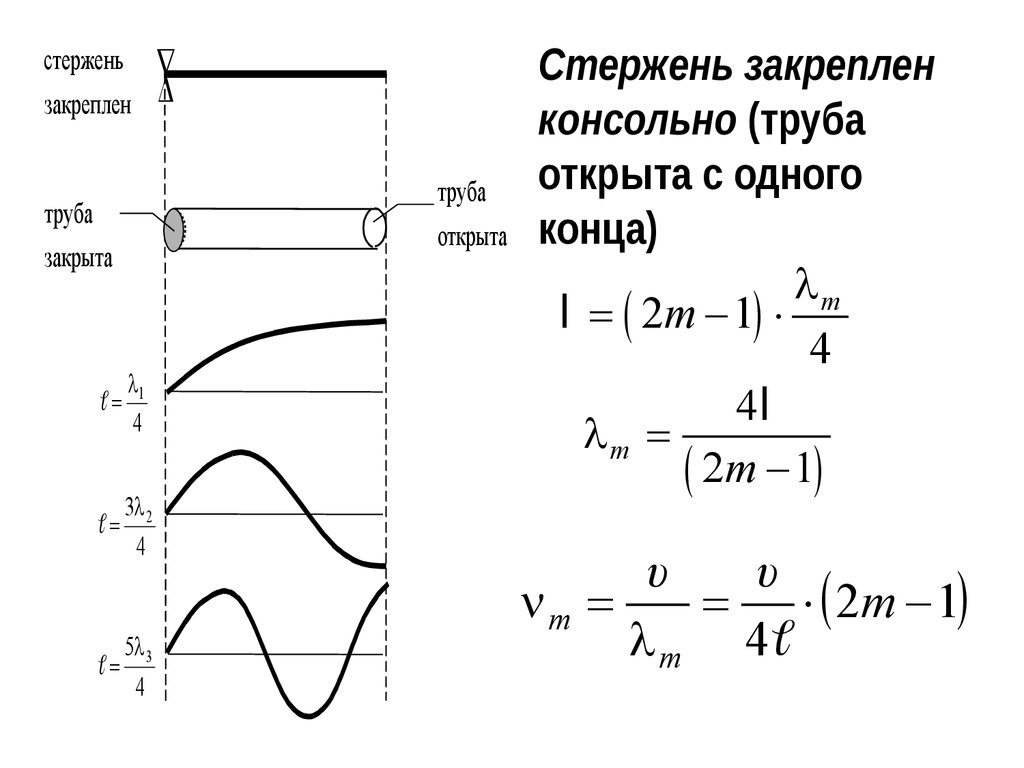
18.
стерженьзакреплен
труба
открыта
труба
закрыта
l1
=
4
=
=
3l 2
4
5l 3
4
Стержень закреплен
консольно (труба
открыта с одного
конца)
lm
l = ( 2m - 1)
4
4l
lm =
( 2m - 1)
υ
υ
m =
= ( 2m - 1)
l m 4
19.
Наименьшие возможные частотыстоячих волн (при m = 1) называются
основными, более высокие частоты
называются обертонами.
20.
Дифракция света21.
Дифракцией света называется отклонениесветового луча от прямолинейного
распространения на резких
неоднородностях среды
21
22.
Дифракциябыла
открыта
Франческо
Гримальди
в
конце
XVII
в.
Объяснение явления дифракции света дано
Томасом Юнгом и Огюстом Френелем, которые
не только дали описание экспериментов по
наблюдению
явлений
интерференции
и
дифракции света, но и объяснили свойство
прямолинейности распространения света с
позиций волновой теории
22
23. Гримальди Франческо 2.IV.1618 - 28.XII.1663
Итальянский ученый. С 1651года - священник.
Открыл дифракцию света,
систематически ее изучал и
сформулировал некоторые
правила. Описал солнечный
спектр, полученный с
помощью призмы. В 1662 г.
определил величину
поверхности Земли.
23
24. Френель Огюст Жан (10.V.1788 - 14.VII.1827)
Французский физик. Научныеработы посвящены физической
оптике.
Дополнил известный принцип
Гюйгенса, введя так называемые
зоны Френеля (принцип
Гюйгенса - Френеля). Разработал
в 1818 году теорию дифракции
света
24
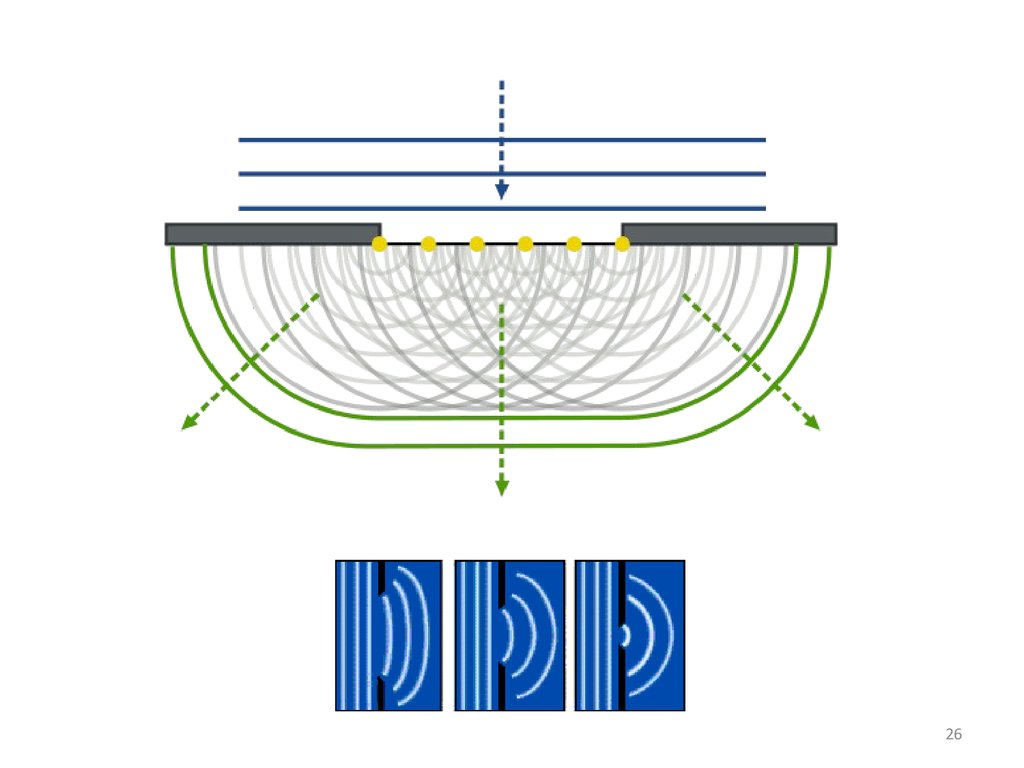
25. Принцип Гюйгенса-Френеля:
Каждыйэлемент волнового фронта можно
рассматривать,
как
центр
вторичного
возмущения,
порождающего
вторичные
сферические
волны,
а
результирующее
световое поле в каждой точке пространства
будет определяться интерференцией этих волн.
25
26.
2627.
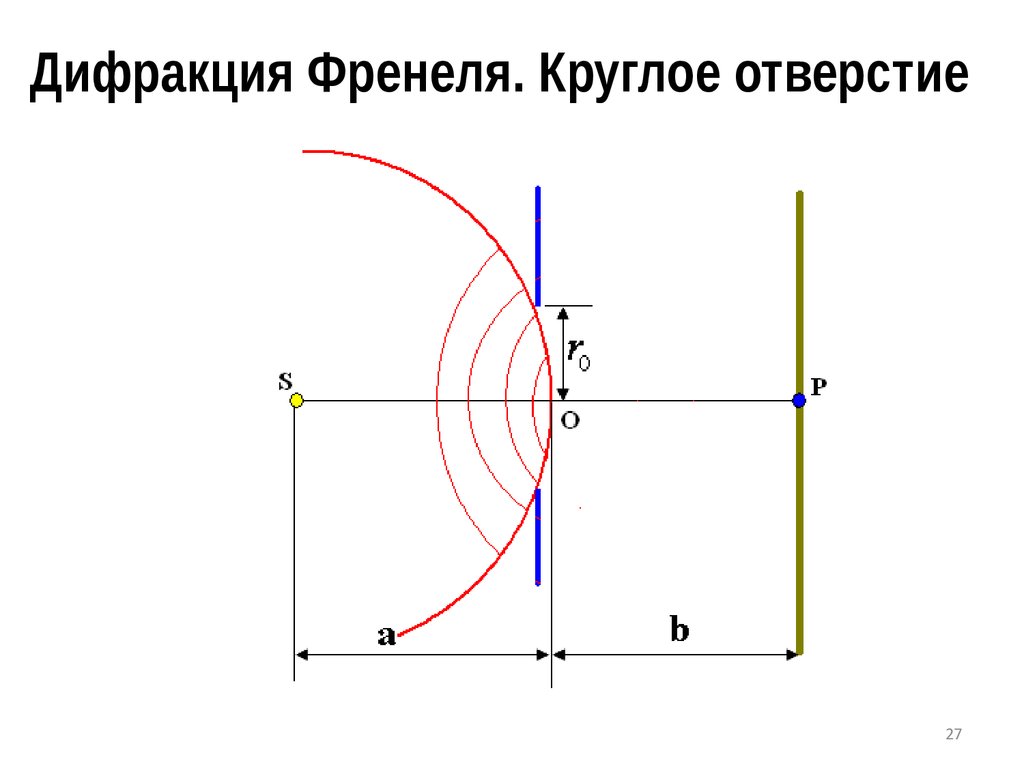
Дифракция Френеля. Круглое отверстие27
28.
Разобьем поверхность волнового фронта,падающего на отверстие, на зоны Френеля по
отношению к точке наблюдения P. Будем
называть открытыми такие зоны Френеля,
которые располагаются внутри отверстия.
Соответственно зоны Френеля, попадающие на
поверхность непрозрачного экрана, называются
закрытыми.
28
29.
Если размер отверстия во много разменьше расстояний от экрана до источника
a и от экрана до точки наблюдения b, то
можно найти число m открытых
отверстием зон Френеля:
2
0
1 1 r
m= +
a b l
29
30.
Суммарная амплитуда в точке наблюдения естьA = A1 – A2 + A3 – A4 + ... ±Am = 0.5(A1±Am)
Амплитуды волн зон Френеля при их
небольшом числе можно считать примерно
одинаковыми.
30
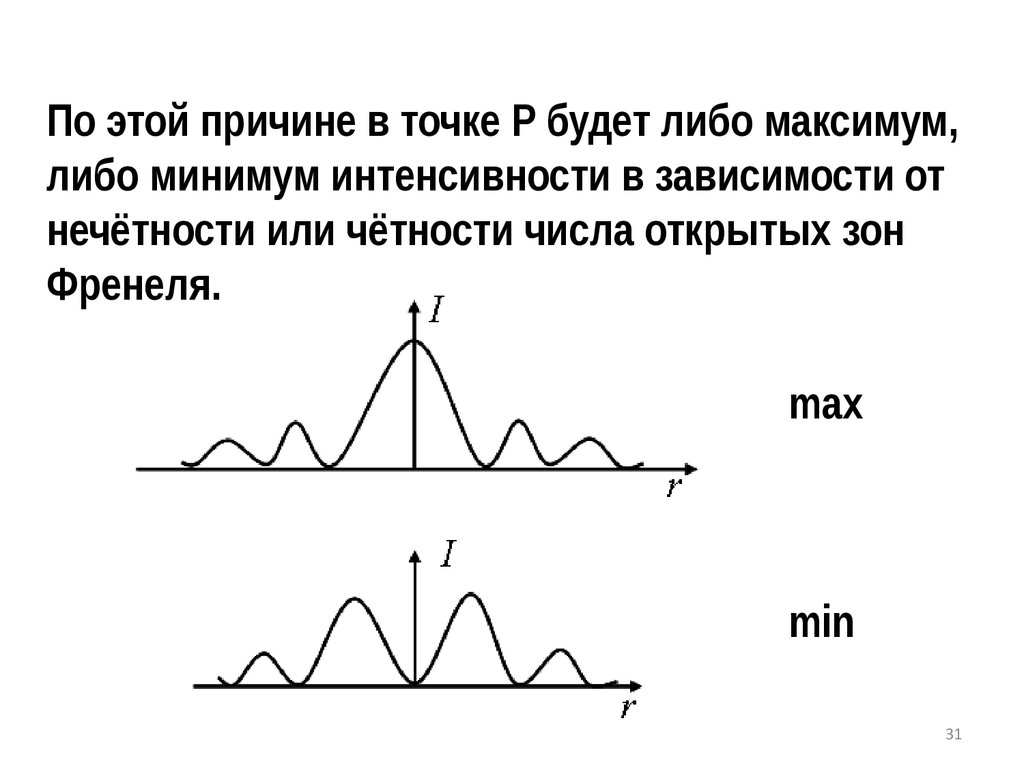
31.
По этой причине в точке Р будет либо максимум,либо минимум интенсивности в зависимости от
нечётности или чётности числа открытых зон
Френеля.
max
min
31
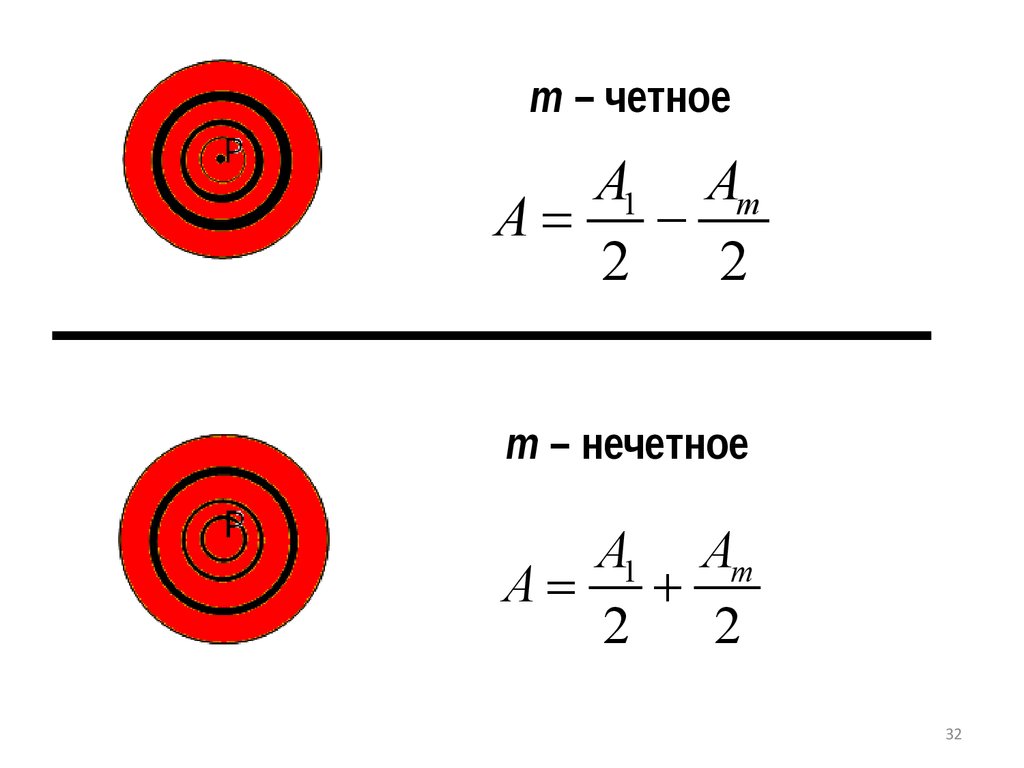
32.
m – четноеA1 Am
A= 2
2
m – нечетное
A1 Am
A=
2
2
32
33.
Интенсивность света в максимумах по мереудаления от центральной точки будет убывать:
- при смещении точки наблюдения P из центра
на периферию открытые из точки P
центральные зоны Френеля частично
закрываются;
- кроме того, частично открываются новые
зоны Френеля, ослабляющие интенсивность
света в точке наблюдения.
33
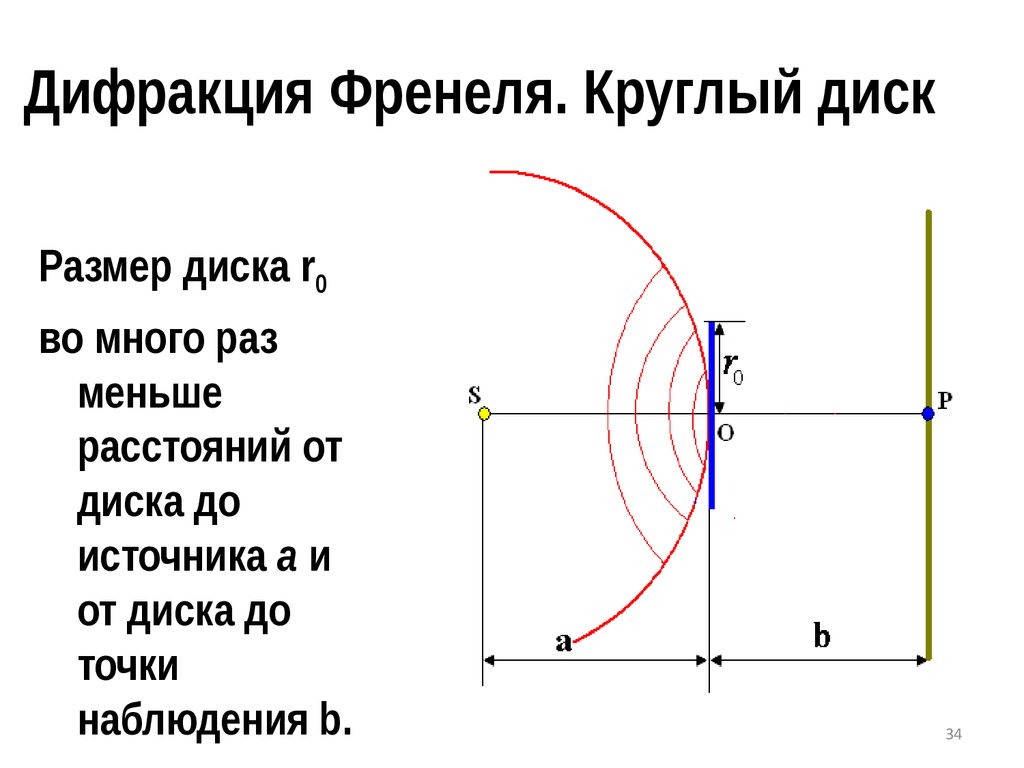
34. Дифракция Френеля. Круглый диск
Размер диска r0во много раз
меньше
расстояний от
диска до
источника a и
от диска до
точки
наблюдения b.
34
35.
Диск из точки наблюдения P закрывает m зонФренеля.
Тогда амплитуда света A в точке наблюдения
будет равна алгебраической сумме амплитуд
волн
A m+1 ,A m+2 ,A m+3 ,....
открытых зон Френеля:
35
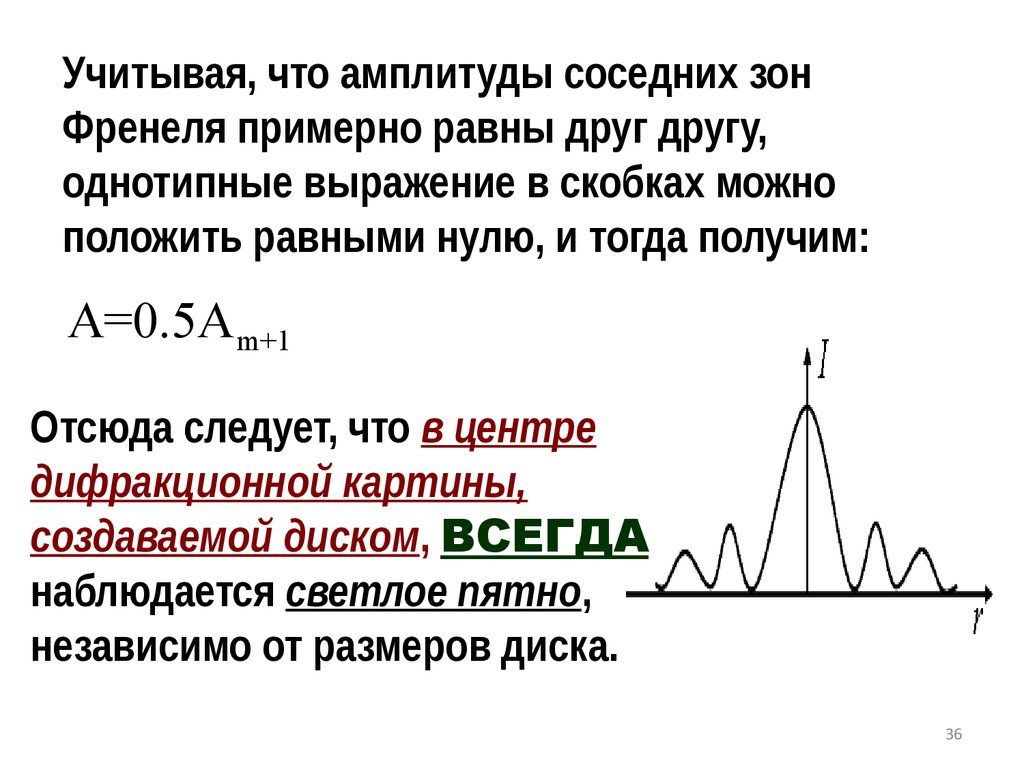
36.
Учитывая, что амплитуды соседних зонФренеля примерно равны друг другу,
однотипные выражение в скобках можно
положить равными нулю, и тогда получим:
A=0.5A m+1
Отсюда следует, что в центре
дифракционной картины,
создаваемой диском, ВСЕГДА
наблюдается светлое пятно,
независимо от размеров диска.
36
37.
Дифракционная картинаот диска, наблюдаемая на
экране, имеет характер
чередующихся тёмных и
светлых колец, в центре
которых находится
светлое пятно.
Структура дифракционной картины света от
непрозрачного диска имеет общие черты с
дифракционной картиной света от отверстия
того же диаметра в непрозрачном экране.
37
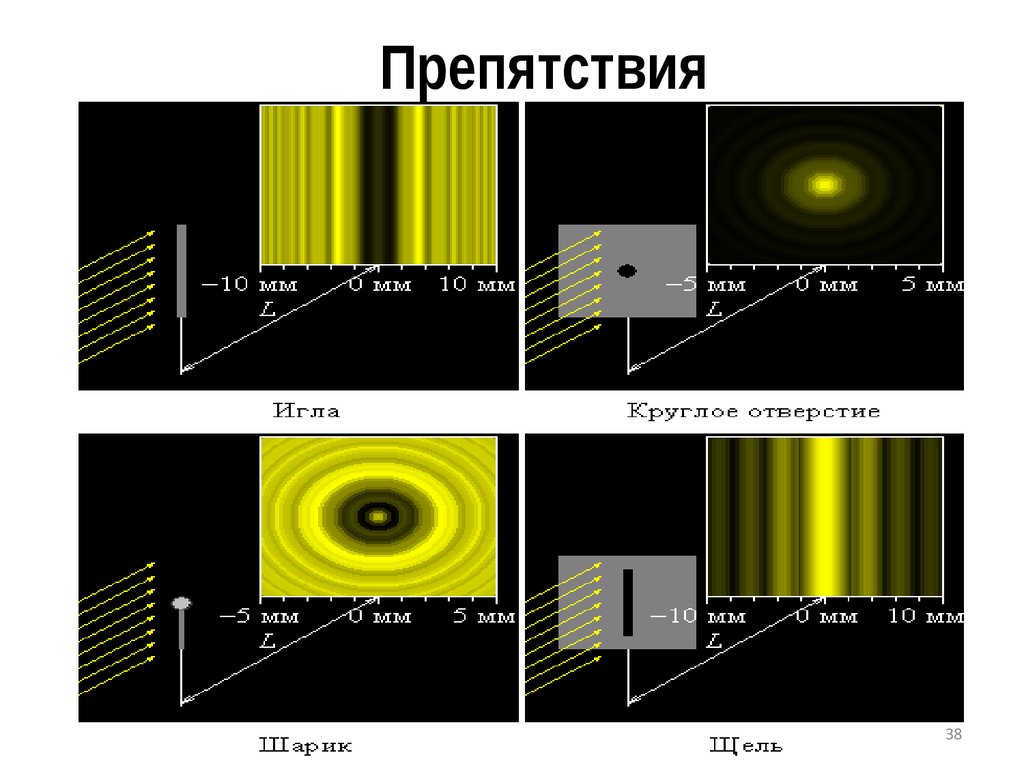
38. Препятствия
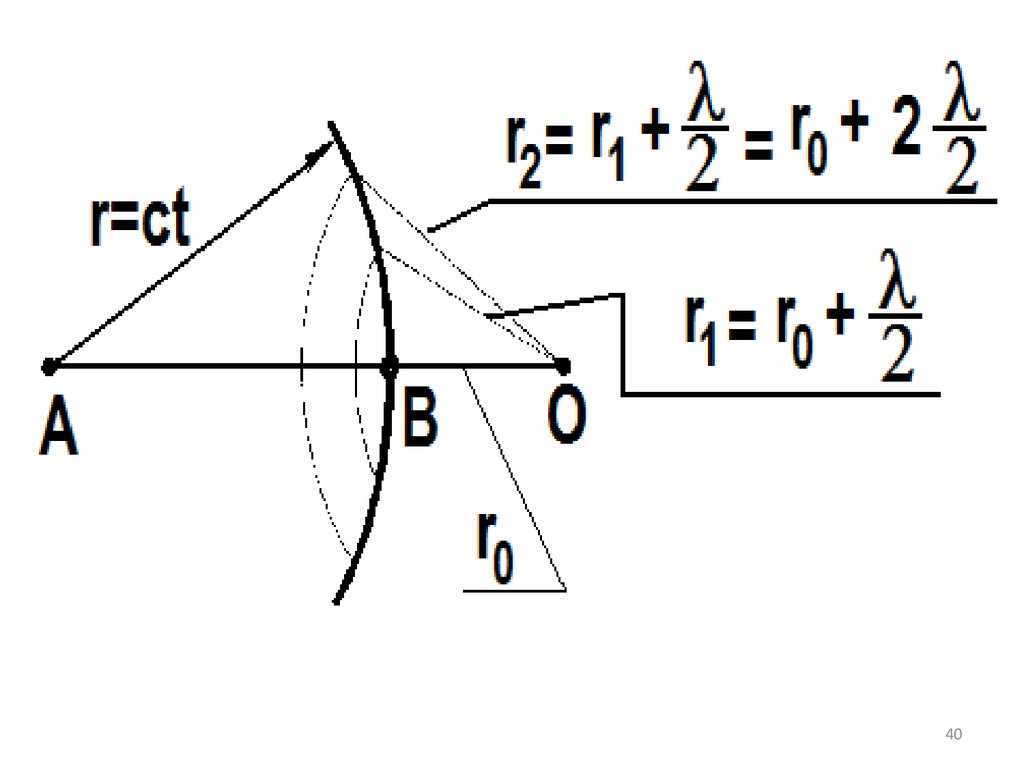
3839. Зоны Френеля
Чтобы найти амплитуду световой волны отточечного монохроматического источника
света А в произвольной точке О изотропной
среды, надо источник света окружить
сферой радиусом r=ct
39
40.
4041.
Интерференция волны от вторичныхисточников, расположенных на этой
поверхности, определяет амплитуду в
рассматриваемой точке P:
необходимо произвести сложение когерентных
колебаний от всех вторичных источников на
волновой поверхности
41
42.
Первая зона Френеля ограничиваетсяточками волновой поверхности, расстояния
от которых до точки О равны:
l
r1 = r0
2
где l — длина световой волны
42
43.
Вторая зона:l
r2 = r1 = r0 l
2
Аналогично определяются границы других зон
43
44. Дифракционные картины
от одного препятствия с разным числомоткрытых зон
44
45.
Если на препятствии укладывается целоечисло длин волн, то они гасят друг друга и в
данной точке наблюдается минимум (темное
пятно). Если нечетное число полуволн, то
наблюдается максимум (светлое пятно)
45
46.
4647. Зонные пластинки
На этомпринципе
основаны
т.н. зонные
пластинки
47
48.
Решите задачу:Найти длину волны падающего света, если
расстояние между источниками равно 0,4 мм,
расстояние до экрана равно 4 м, а расстояние
между интерференционными максимумами
равно 5 мм.
49.
Контрольные вопросы1. Решите задачу:
Найти длину волны падающего света, если расстояние
между источниками равно 0,4 мм, расстояние до
экрана равно 4 м, а расстояние между
интерференционными максимумами равно 5 мм.
2. Оптическая разность хода при интерференции на
тонких пленках
3. Стоячие волны: причины образования, энергия,
координаты пучностей и узлов
4. Определение дифракции. Принцип Гюйгенса-Френеля
5. Зоны Френеля. Дифракция на круглом диске и на
круглом отверстии: сходство и различия

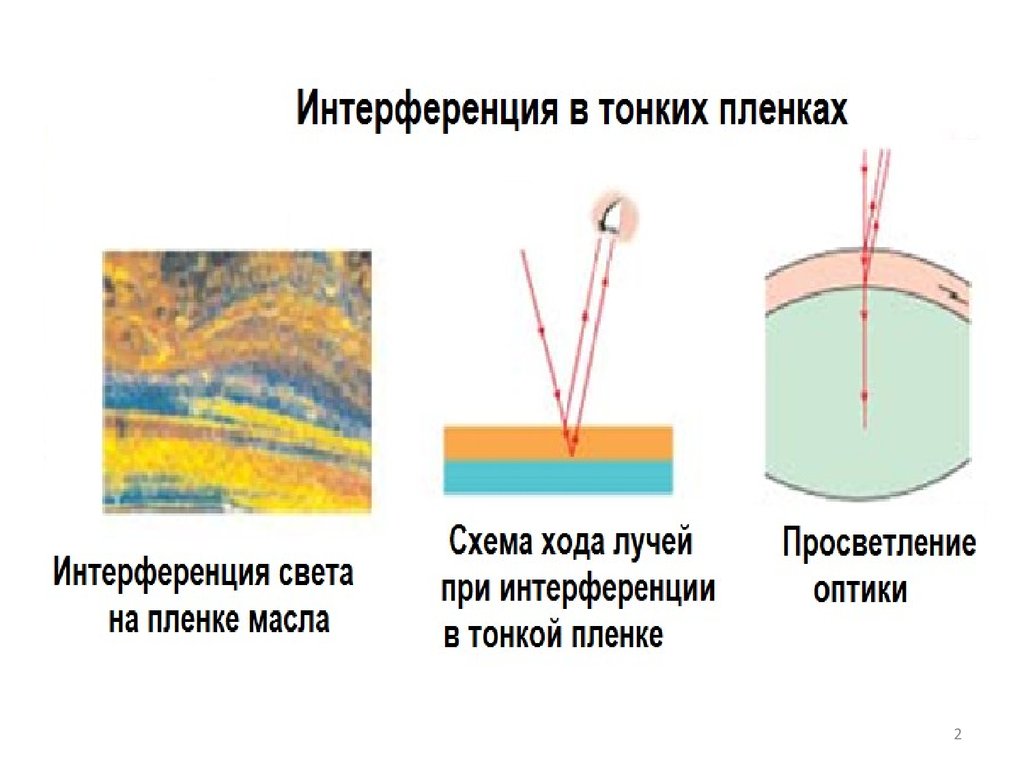































 Физика
Физика








