Похожие презентации:
Скалярное произведение векторов
1.
2.
Угол между векторамиb
a
a
b
Лучи ОА и ОВ образуют АОВ.
Градусную меру этого угла
обозначим буквой
Угол между векторами и
равен
3.
Найти углы между векторамиДва вектора называются
перпендикулярными,
если угол между ними равен 90 .
4.
№ 441 (а – г)АВСDA1B1C1D1 – куб.
Найдите угол между
векторами.
D1
A1
C1
B1
D
C
A
B
5.
№ 442 Угол между векторами АВ и СDравен . Найдите углы между векторами
B
А
j
j
(A)
O (C)
D
C
6.
Сумма векторов – вектор.Разность векторов – вектор.
Произведение вектора на число – вектор.
Скалярным произведением двух векторов
называется произведение их длин на косинус
угла между ними.
a b = a b cos(a b )
Скалярное произведение векторов – число (скаляр).
Скаляр – лат. scale
– лестница, шкала.
Ввел в 1845г. У. Гамильтон, английский математик.
7.
Скалярное произведение в физикеСкалярное произведение векторов
встречается в физике. Например,
из курса механики известно, что
F
j
M
N
работа A постоянной силы F при
перемещении тела из точки M в
точку N равна произведению силы F и перемещения
MN на косинус угла между ними.
A = F MN cos j
A = F MN
8.
a b = 900b
a
Если векторы a и b перпендикулярны, то
скалярное произведение векторов равно нулю.
Обратно: если a b =
перпендикулярны.
0 , то векторы a и b
9.
ba
Скалярное произведение ненулевых векторов
положительно тогда и только тогда , когда
угол между векторами
10.
ba
Скалярное произведение ненулевых векторов
отрицательно тогда и только тогда , когда угол
между векторами
11.
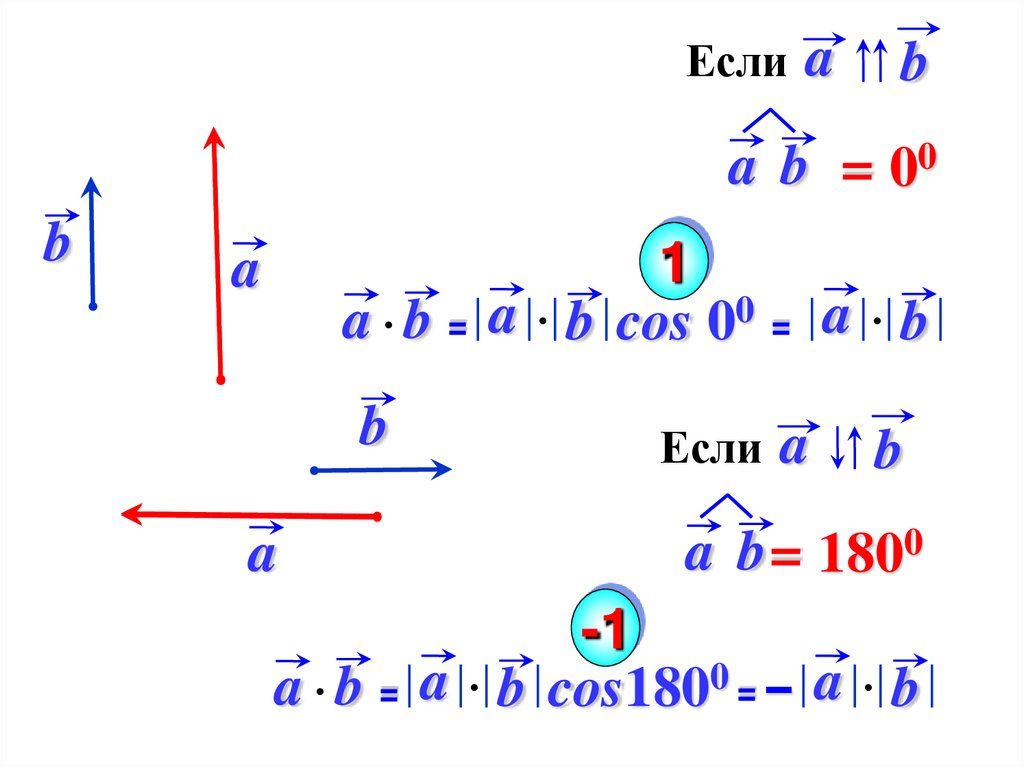
Еслиa
b
a b = 00
b
a
a b =
b
a
a b =
1
a b cos 00 = a b
Если
a
b
a b = 1800
-1
a b cos1800 = – a b
12.
a a = 00a
1
Скалярное произведение
скалярным квадратом вектора
называется
и обознач
13.
Скалярное произведение векторова х1; у1; z1
b х2 ; у2 ; z2
а b х1 х2 у1 у2 z1 z2
14.
а b а b cos a, bcos a, b
а b
а b
х1 х2 у1 у2 z1 z2
х у z х у2 z2
2
1
2
1
2
1
2
2
2
2
15.
№ 443 АВСDA1B1C1D1 – куб. Найдитескалярное произведение векторов
AC C A
D B AC
BA BC
D1
AD B1C1
1
1
C1
O1
A1
B1
1
1
a
1
A1O1 A1C1
D1O1 B1O1
BO1 C1B
D
300
A
a
B
C
16.
Все ребра тетраэдра АВСD равны друг другу. Точки М иN – середины ребер АD и ВС. Докажите, что MN AD = 0
A
M
D
B
N
C
17.
xOyI
Маленький тест
На каком расстоянии от плоскости
находится точка А(2; -3; 5)
z
3
3
I
I
I
I
I
O
I
5
I
2
ВЕРНО!
I
2
I
1
ПОДУМАЙ
!
I
I
M
Проверка
I
I
ПОДУМАЙ
!
x
Oxy
I
I
I
y
18.
Iz
I
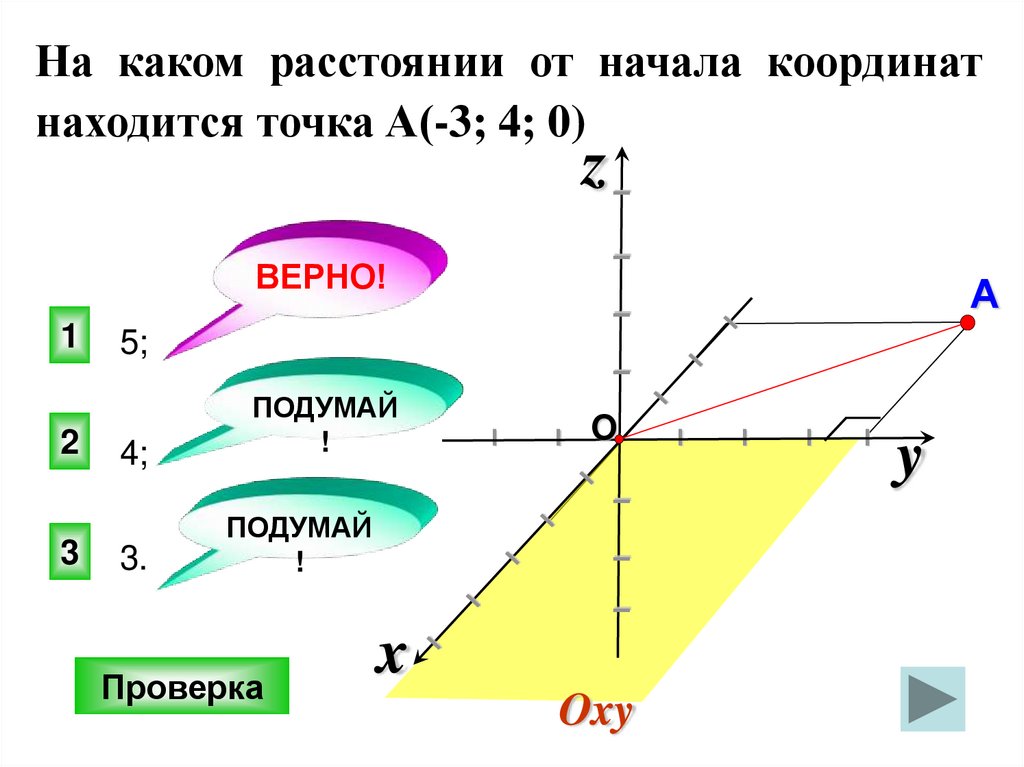
На каком расстоянии от начала координат
находится точка А(-3; 4; 0)
А
I
ВЕРНО!
5;
I
1
4;
I
I
O
I
2
ПОДУМАЙ
!
I
3.
I
3
ПОДУМАЙ
!
Проверка
x
Oxy
I
I
I
I
y
19.
Найти координаты середины отрезка, если концы егоимеют координаты
A(-3; 2;-4)
и
B(1;-4; 2)
C( -3 + 1 ;2+(-4); -4+2 )
1
C(-2; 1;-1)
2
C(-1;-1;-1)
3
C(-2;-2;-2)
Проверка
ПОДУМАЙ
!
ВЕРНО!
ПОДУМАЙ
!
2
2
2
20.
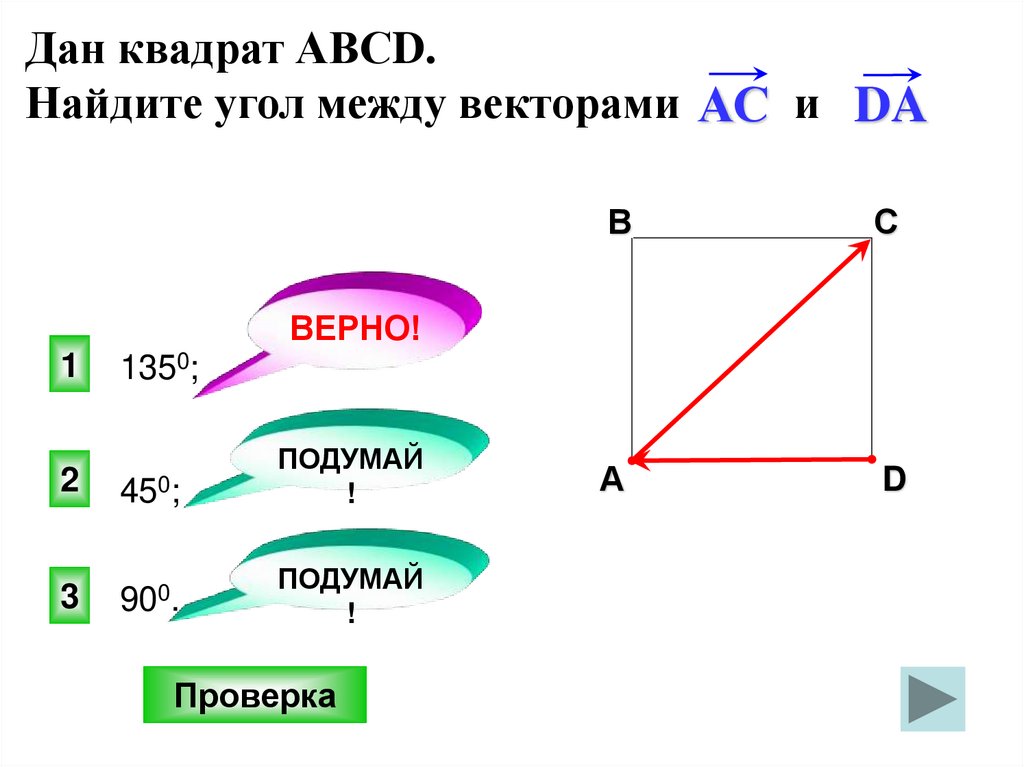
Дан квадрат АВСD.Найдите угол между векторами АС и DA.
В
С
А
D
ВЕРНО!
1
1350;
2
450;
ПОДУМАЙ
!
3
900.
ПОДУМАЙ
!
Проверка
21.
II
I
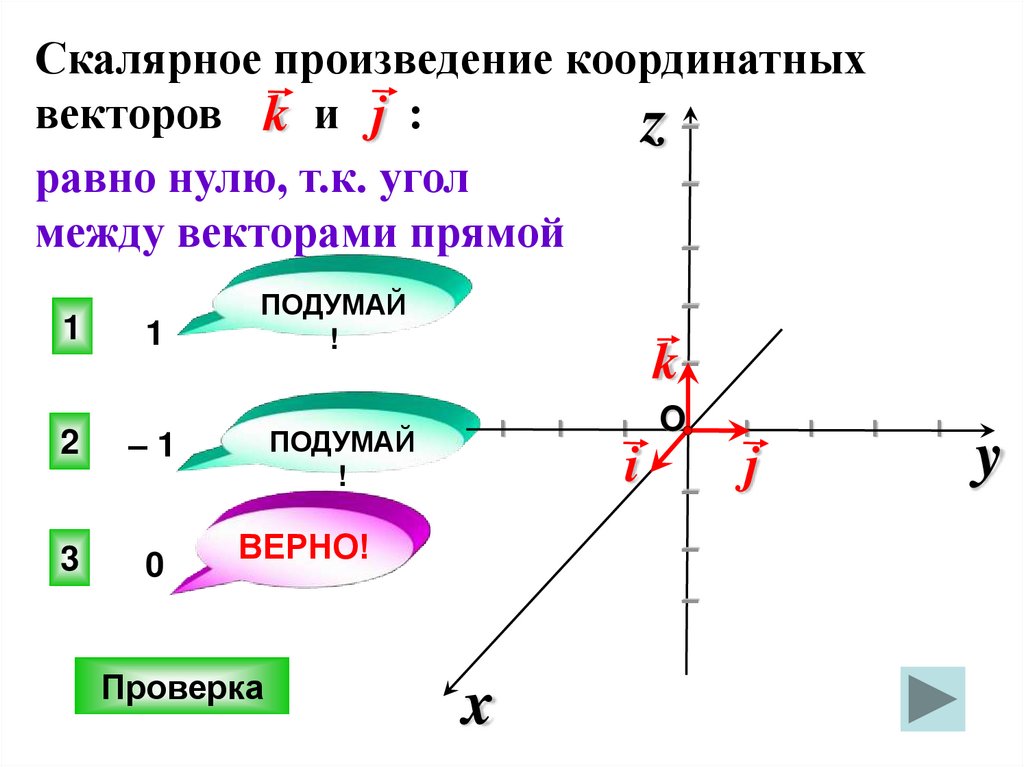
Скалярное произведение координатных
векторов k и j :
z
равно нулю, т.к. угол
между векторами прямой
–1
3
0
ПОДУМАЙ
!
I
I
i
ВЕРНО!
I
I
I
O
I
2
k
I
1
I
1
ПОДУМАЙ
!
Проверка
x
I
j
I
I
I
y
22.
Скалярный квадрат вектораВЕРНО!
1
49
2
7
ПОДУМАЙ
!
3
1
ПОДУМАЙ
!
Проверка
равен:
Скалярный квадрат вектора
равен квадрату его длины.
(7i)2 = 7i 2 = 72 = 49
23.
Записать координаты вектора nПОДУМАЙ!
1
n {-8; 1; 0}
2
n {1;-8; 0}
3
n {1; 0;-8}
ВЕРНО!
ПОДУМАЙ!
= – 8j + i
24.
Найдите угол между векторамиm n = –15,
ПОДУМАЙ!
1
500
ПОДУМАЙ!
2
3
600
1200
Проверка
ВЕРНО!
m = 5,
m и n, если
n = 6.
25.
ABCDA1B1C1D1 – куб, ребро которого равно 1.Найдите скалярное произведение векторов AD1
и ВС .
2
0
BC1 BC BC1 BC cos 45 1 2
1
2
1
2
4;
2;
ПОДУМАЙ
!
D1
A1
3
B1
ПОДУМАЙ
!
ВЕРНО!
C1
D
1.
C
Проверка (3)
A
B
26.
1) Какие операции над векторами мы можемвыполнять?
- Сложение, вычитание, умножение на число
и скалярное произведение векторов.
2) Скажите, что нужно знать для нахождения
скалярного произведения?
- Длины векторов и угол между ними
3) Чем отличаемся изученное действие от
предыдущих?
- В результате получается всегда число.
27.
a b a b cosa b 0
Если
a b, то
Если
a b , то cos180 1 a b a b
Если
а b
Если
cos 90 0
0
0
, то cos 0 1
0
a b a b
2
a b , то a b a a a a a a
2























 Математика
Математика








