Похожие презентации:
Скалярное произведение векторов
1.
2.
Угол между векторамиb
А
В
a
a
b
a b= a
О
Лучи ОА и ОВ образуют угол АОВ.
Градусную меру этого угла
обозначим буквой a
a
Угол между векторами
равен a
a
и
b
3.
Найти углы между векторами.f
a
d 30
b
c
a
a b=
300
a c = 1200
d
0
f
b c = 900
b
d c = 1800
Два вектора называются
перпендикулярными,
если угол между ними равен 900.
b^c
b ^d
b^f
d f = 00
4.
№ 441 АВСDA1B1C1D1 – куб.Найдите угол между векторами.
D1
A1
C1
0
В1В, В1С = 45
0
DА, B1D1 = 135
А1C1, A1B = 600
BC, AС =
B1
450
0
B1C, AD1 = 90
D
C
A
B
0
BB1, AC = 90
0
А1D1, BC = 0
AА1, C1C = 1800
5.
j.№ 442 Угол между векторами АВ и СD равен
Найдите углы между векторами
ВА, DС = j
B
ВА, СD = 1800–j
АB, DC =
А
j
j
(A)
O (C)
D
C
6.
Сумма векторов – вектор.Разность векторов – вектор.
Произведение вектора на число – вектор.
Скалярным произведением двух векторов
называется произведение их длин на косинус
угла между ними.
a b = a b cos(a b )
Скалярное произведение векторов – число (скаляр).
Скаляр – лат. scale
– лестница, шкала.
Ввел в 1845г. У. Гамильтон, английский математик.
7.
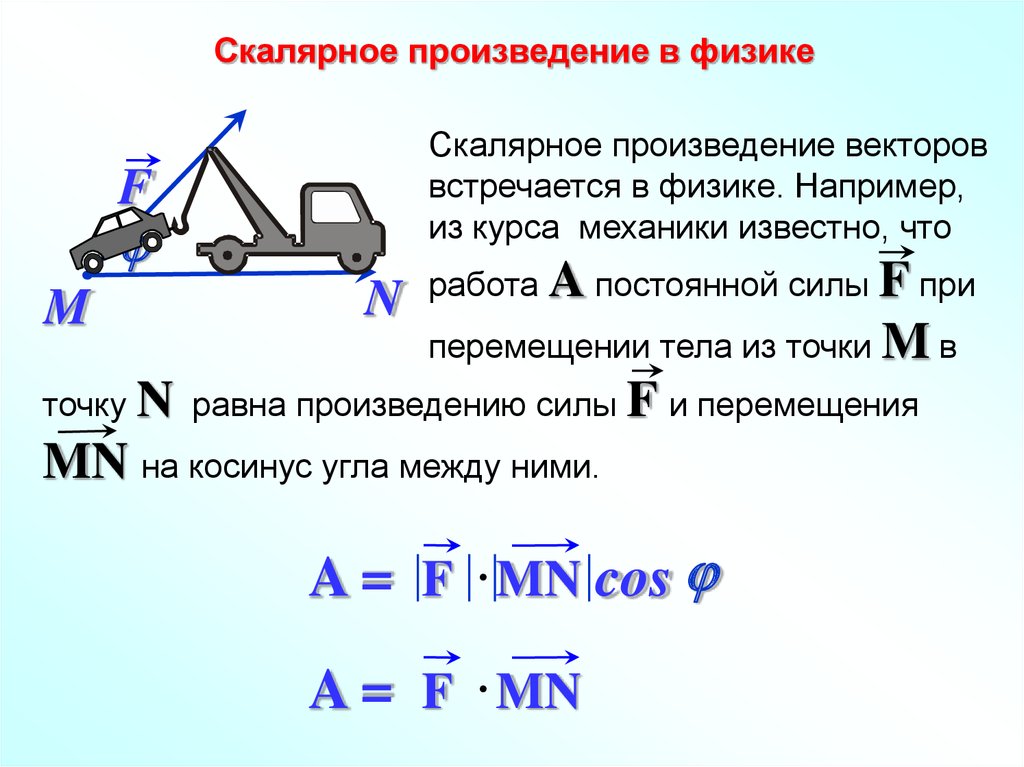
Скалярное произведение в физикеСкалярное произведение векторов
встречается в физике. Например,
из курса механики известно, что
F
j
M
N
работа A постоянной силы F при
перемещении тела из точки M в
точку N равна произведению силы F и перемещения
MN на косинус угла между ними.
A = F MN cos j
A = F MN
8.
0a b = 900
b
a b = a b cos 900
=0
a
a
b
Если векторы
и
перпендикулярны, то
скалярное произведение векторов равно нулю.
a b = 0 , то векторы a
Обратно: если
перпендикулярны.
и
b
Скалярное произведение ненулевых векторов равно
нулю тогда и только тогда, когда эти векторы
перпендикулярны.
a b = 0
a ^b
9.
a b < 900a b =
b
>0
a b cos a > 0
a
Скалярное произведение ненулевых векторов
положительно тогда и только тогда , когда угол между
векторами острый.
a b > 0 a b < 900
10.
a b > 900a b =
b
<0
a b cos a < 0
a
Скалярное произведение ненулевых векторов
отрицательно тогда и только тогда , когда угол между
векторами тупой.
a b < 0 a b > 900
11.
Еслиa
b
a b = 00
b
a
a b =
b
a
a b =
1
a b cos 00 = a b
Если
a
b
a b = 1800
-1
a b cos1800 = – a b
12.
a a = 00a
a a =
1
a a cos 00 = a a
Скалярное произведение
a a
скалярным квадратом вектора
=
a
2
называется
a
и обозначается
a2
Таким образом,
скалярный квадрат вектора равен квадрату его длины.
a2
=
a
2
13.
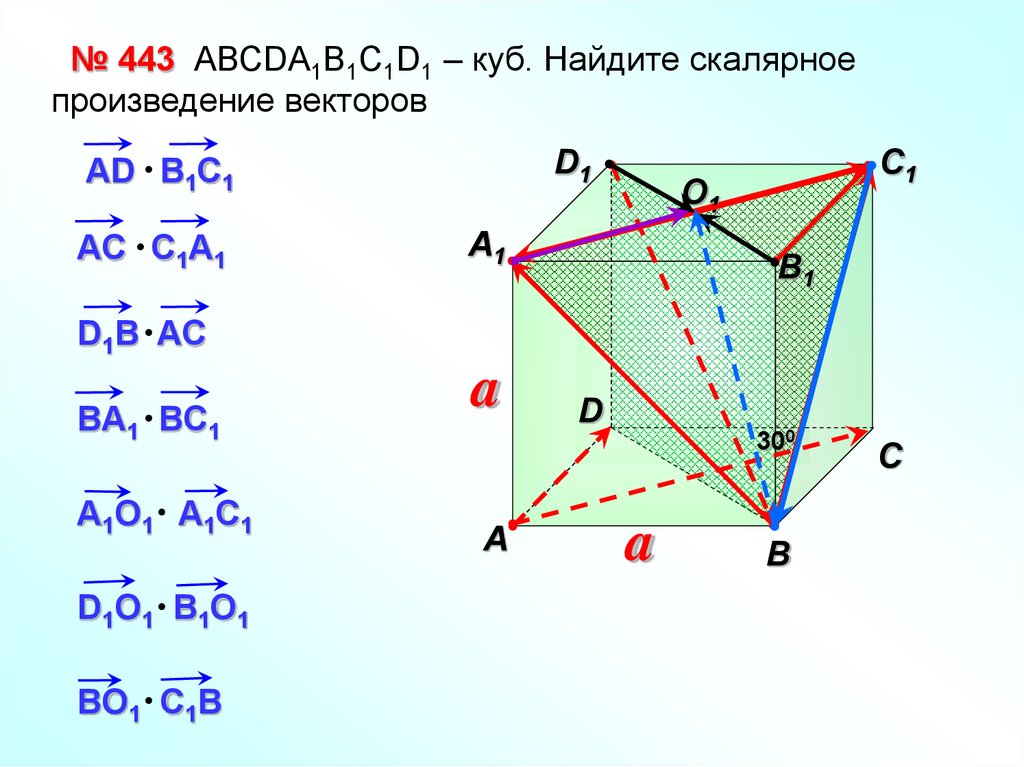
№ 443 АВСDA1B1C1D1 – куб. Найдите скалярноепроизведение векторов
AC C A
D B AC
BA BC
D1
AD B1C1
1
1
C1
O1
A1
B1
1
1
a
1
A1O1 A1C1
D1O1 B1O1
BO1 C1B
D
300
A
a
B
C
14.
Все ребра тетраэдра АВСD равны друг другу. Точки М иN – середины ребер АD и ВС. Докажите, что MN AD = 0
A
M
D
B
N
C
15.
xOy находится точкаz
I
Маленький тест
На каком расстоянии от плоскости
А(2; -3; 5)
3
3
I
I
I
I
I
O
I
5
I
2
ВЕРНО!
I
2
I
1
ПОДУМАЙ
!
I
I
M
Проверка
I
I
ПОДУМАЙ
!
x
Oxy
I
I
I
y
16.
Iz
I
На каком расстоянии от начала координат находится точка
А(-3; 4; 0)
А
I
ВЕРНО!
5;
I
1
4;
I
I
O
I
2
ПОДУМАЙ
!
I
3.
I
3
ПОДУМАЙ
!
Проверка
x
Oxy
I
I
I
I
y
17.
Найти координаты середины отрезка, если концы егоимеют координаты
A(-3; 2;-4)
и
B(1;-4; 2)
C( -3 + 1 ;2+(-4); -4+2 )
1
C(-2; 1;-1)
2
C(-1;-1;-1)
3
C(-2;-2;-2)
Проверка
ПОДУМАЙ
!
ВЕРНО!
ПОДУМАЙ
!
2
2
2
18.
Дан квадрат АВСD.Найдите угол между векторами АС и DA.
В
С
А
D
ВЕРНО!
1
1350;
2
450;
ПОДУМАЙ
!
3
900.
ПОДУМАЙ
!
Проверка
19.
j:
z
1
–1
3
0
I
I
k
I
ПОДУМАЙ
!
I
I
i
ВЕРНО!
O
I
2
ПОДУМАЙ
!
I
1
I
равно нулю, т.к. угол между
векторами прямой
I
и
I
k
I
Скалярное произведение координатных векторов
Проверка
x
I
j
I
I
I
y
20.
Скалярный квадрат вектораВЕРНО!
1
7i
равен:
Скалярный квадрат вектора
равен квадрату его длины.
49
2
7
ПОДУМАЙ
!
3
1
ПОДУМАЙ
!
Проверка
(7i)2 = 7i 2 = 72 = 49
21.
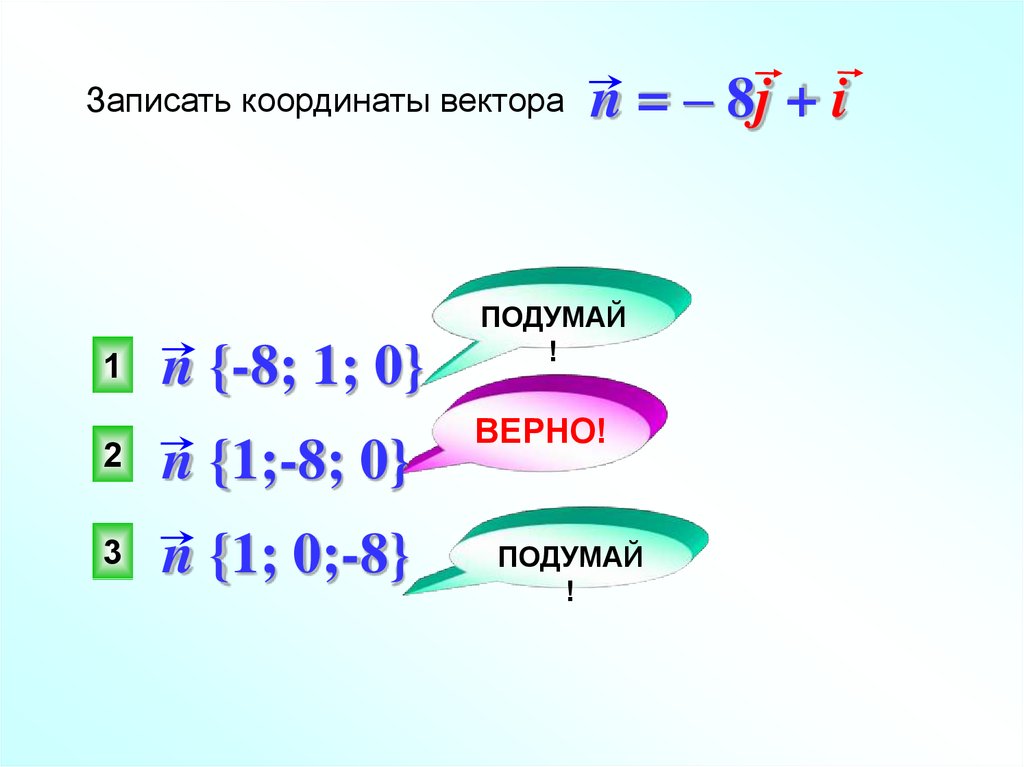
Записать координаты вектора1
n {-8; 1; 0}
2
n {1;-8; 0}
3
n {1; 0;-8}
n = – 8j + i
ПОДУМАЙ
!
ВЕРНО!
ПОДУМАЙ
!
22.
m и n, еслиm = 5, n = 6.
Найдите угол между векторами
m n = –15,
1
2
3
500
ПОДУМАЙ
!
ПОДУМАЙ
!
600
1200
ВЕРНО!
Скалярное произведение ненулевых
векторов отрицательно тогда и только
тогда , когда угол между векторами тупой
Проверка
23.
ABCDA1B1C1D1 – куб, ребро которого равно 1.Найдите скалярное произведение векторов АD1 и BC.
2
BC1 BC BC1 BC cos 45 1 2
1
2
0
1
2
4;
2;
ПОДУМАЙ
!
D1
A1
3
B1
ПОДУМАЙ
!
ВЕРНО!
C1
D
1.
C
Проверка (3)
A
B
24.
Скалярное произведение векторовa {x1; y1;z1}
b {x2; y2;z2}
и
a b = x1x2 + y1y2+z1z2
выражается формулой
Пример
Найдите скалярное произведение
векторов
b {-2;
-2 11;-7}
-7
-3
d { 55; 44;-3}
+ + ( ) ( ) = 15
25.
№ 444Даны векторы
a {1; -1; 2}, b {-1; 1; 1}, c {5; 6; 2}
Вычислить
a c = 1 5 + (-1) 6 + 2 2 = 3
a b = 1 (-1) + (-1) 1 + 2 1 = 0
b c =
-1 5 + 1 6 + 1 2 = 3
a a = 1 1 + (-1) (-1) + 2 2 = 6
b b =
-1 (-1) + 1 1 + 1 1 =
3
26.
Скалярное произведение векторовЧерез длины векторов
и угол между ними
в координатах
a b = a b cos(a b ) a b = x1x2+y1y2+z1z2
a b =0
a ^b
a b > 0 a b < 900
a b < 0 a b > 900
a2
=
a
2
27.
a {3; -4; 2}, b {-2; 1; 3}, c {-2;-1,5; 0}Найдите
a b = 3 (-2) + (-4) 1 + 2 3
=-4
тупой
b c = (-2) (-2) + 1 (- 1,5) + 3 0 = 2,5
острый
c a = 3 (-2) + (-4) (- 1,5) + 2 0 = 0
прямой
Перпендикулярны ли векторы
a и b, b и c, c и a
Каким (острым, тупым или прямым) является угол между
векторами
a
и
b, b и c, c
и
a
28.
Косинус угла между ненулевыми векторамиaи b
выражается формулой
cos a =
x1 x2 + y 1 y2 + z 1 z 2
x12 + y12 + z12 x22 + y22 + z22
29.
Доказательство:a b = x1x2 + y1y2+ z1z2
2 + y 2+ z 2
a
=
x
1
1
1
a b =
cosa
cosa
2+ y 2+ z 2
x
b
=
2
2
2
a b cosa
=
=
a b
a b
30.
Свойства скалярного произведения векторовa b, c
Для любых векторов
,
справедливы равенства:
1
a 2 0
2
a b
3
(a + b) c
=
причем
b a
=
a 2> 0
и любого числа
при
k
a 0
Переместительный
закон
a c + b c
Распределительный закон
4
(ka) b = k(a b) Сочетательный закон
31.
(a + b) c=
a c + b c
Распределительный закон
имеет место для любого числа слагаемых.
Например,
( a + b + c ) d
=
a d + b d + c d
32.
№ 462. ABCDA1B1C1D1 – прямоугольный параллелепипед,0
0
АА1=АВ=АD=1, DAB 60 , А1 АD A1 AB 90
а) ВА
D C
1
1
= 1 1 cos1800
B1
A1
C1
D1
1
B
C
1
A
600
D
1
33.
№ 462. б) ВC1 D1BC1 (0;1;1)
B1
A1
D1 (
ВC1{0;1;1}
B
1
C
1
A
1
3; ;1)
2 2
3
2
600
1
2
D
1
D1B {-
1
2
;-3 ;-1}
2
34.
№ 462.в) АС1
АC1 = 2 2 cos00
из АСD : AC 12 12 2 1 1cos1200
1 способ
AC 3
B1
C1
D1
A1
AC1 1
2
AC1 2
B
1
C
1
1200
D
600
A
1
из АСС1 :
3
2
35.
№ 462.в) АС1
АC1
2 способ
C1 (0;1;1)
B1
D1
A1
1
B
1
1
2
C
3
2
600
A
3 1
( ;- ;0)
2 2
АС1{-
D
1
3 3
; ; 1}
2 2
36.
№ 462.г)
IDB1I
из АВD : ВD 1
B1
C1
DB1 12 12
D1
A1
DB1 2
B
1
C
1
1
600
D
A
1
из DBB1 :
37.
№ 462. е)cos(DA1 D1B)
B1
(
C1
1
3;- ;1)
2 2
A1
D1 (
B
1
C
1
A
1
3; ;1)
2 2
3
2
600
1
2
D(
1
1
3; ;0)
2 2
D1B {-
1
2
;-3 ;-1}
2
DA1 {0;- 1; 1}
38.
Применение скалярного произведениядля вычисления угла между прямыми/
Ненулевой вектор называется направляющим
вектором прямой a , если он лежит либо на
прямой a , либо на прямой, параллельной
B
A
c
a.
a
39.
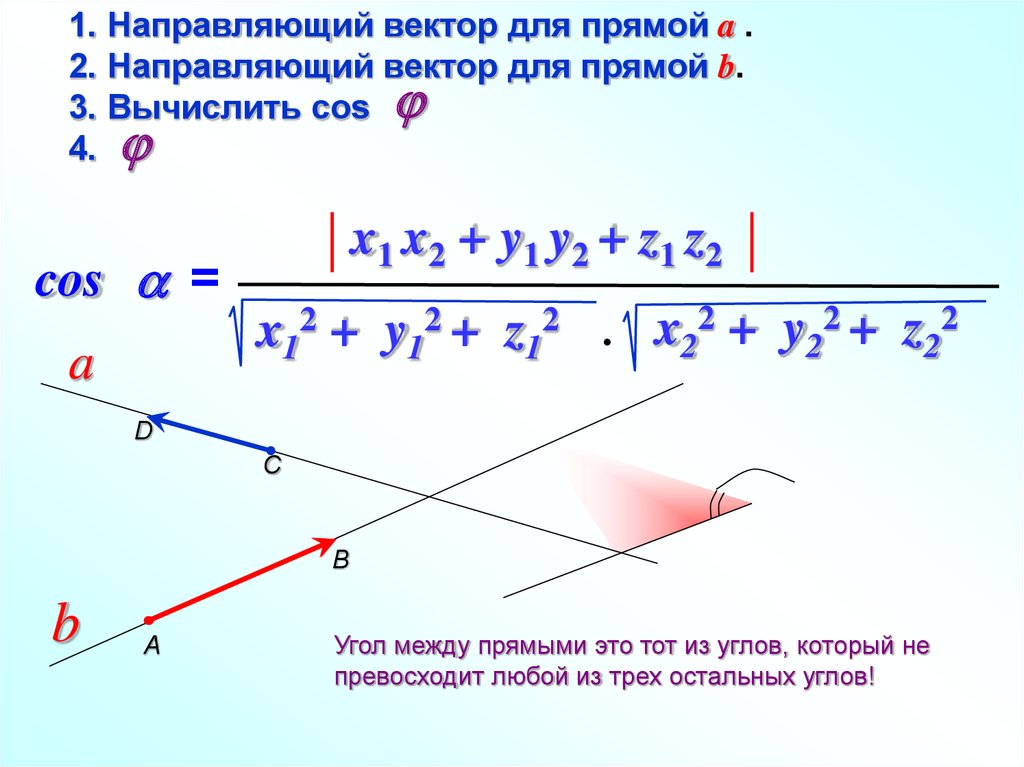
1. Направляющий вектор для прямой a .2. Направляющий вектор для прямой b.
3. Вычислить cos j
4. j
cos a =
a
x1 x2 + y1 y2 + z1 z2
x12 + y12 + z12 x22 + y22 + z22
D
C
B
b
A
Угол между прямыми это тот из углов, который не
превосходит любой из трех остальных углов!
40.
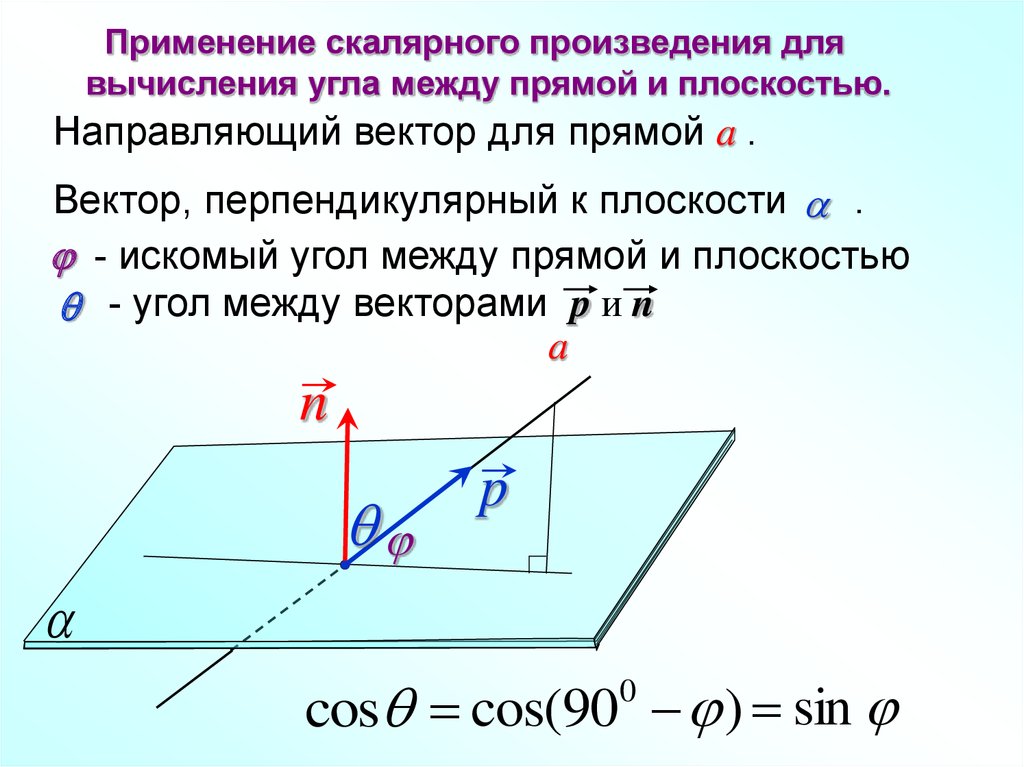
Применение скалярного произведения длявычисления угла между прямой и плоскостью.
Направляющий вектор для прямой a .
Вектор, перпендикулярный к плоскости a .
j - искомый угол между прямой и плоскостью
q - угол между векторами p и n
a
n
qj
p
a
cosq cos(90 j ) sin j
0
41.
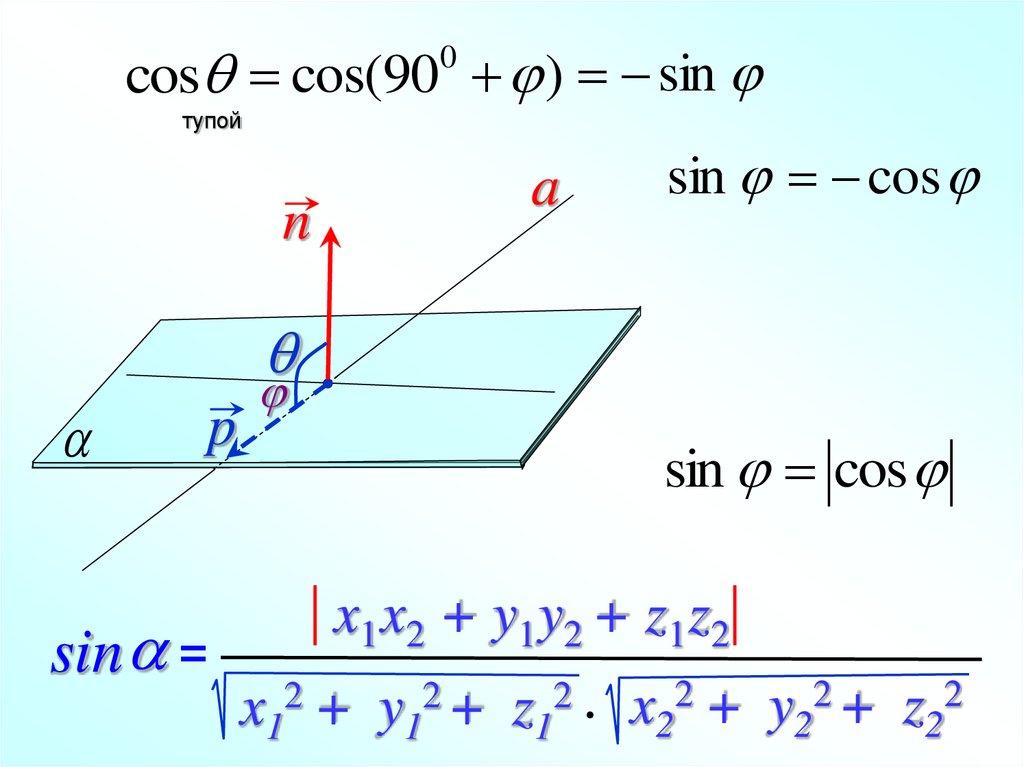
cosq cos(90 j ) sin j0
тупой
a
n
sin j cos j
q
a
p
sin a =
j
sin j cos j
x1 x2 + y1 y2 + z 1 z 2
x12
+
y12 +
z12
x22 + y22 + z22
42.
Применение скалярного произведения длявычисления угла между прямой и плоскостью.
1. Направляющий вектор для прямой a .
2. Вектор, перпендикулярный к плоскости
3. Вычислить sin j
4. j
sin a =
a.
x1 x2 + y1 y2 + z1 z2
x12 + y12 + z12 x22 + y22 + z22




































 Математика
Математика








