Похожие презентации:
Математическое ожидание и дисперсия непрерывных величин
1.
Смысл математического ожидания и дисперсииостается таким же, как и в случае дискретных
случайных величин. Меняется вид формул для
их нахождения путем замены:
xi x
pi f ( x)dx
Тогда
получаем
формулы
для
расчета
математического
ожидания
и
дисперсии
непрерывной случайной величины:
2.
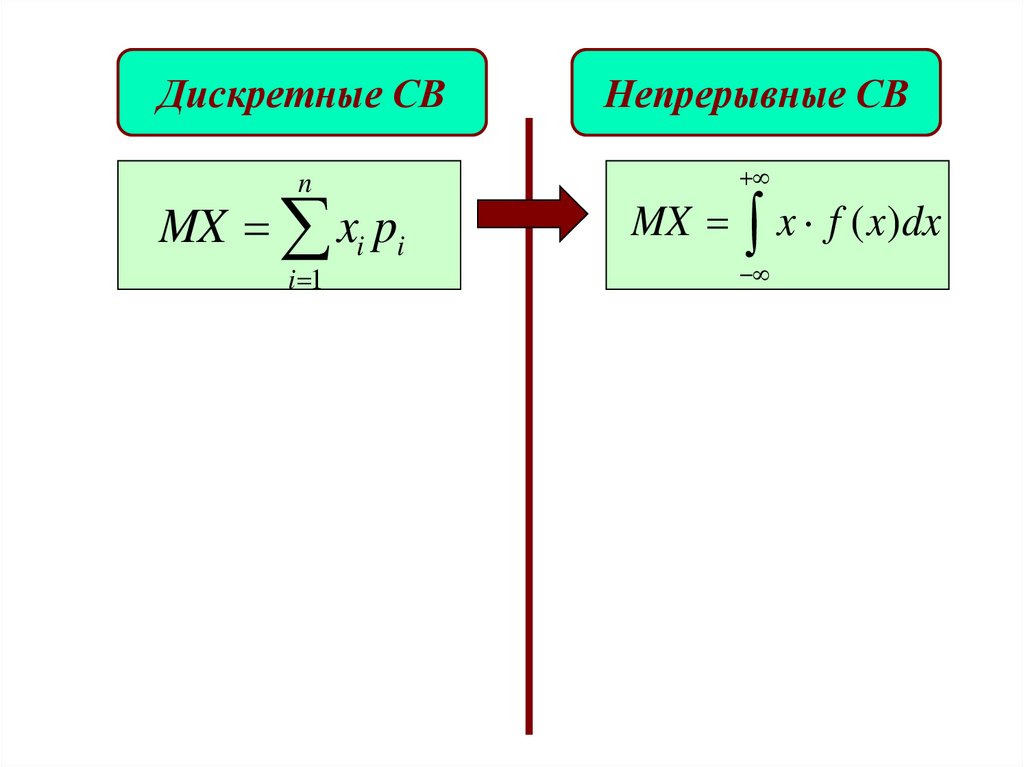
Дискретные СВНепрерывные СВ
n
MX xi pi
i 1
MX
x f ( x)dx
3.
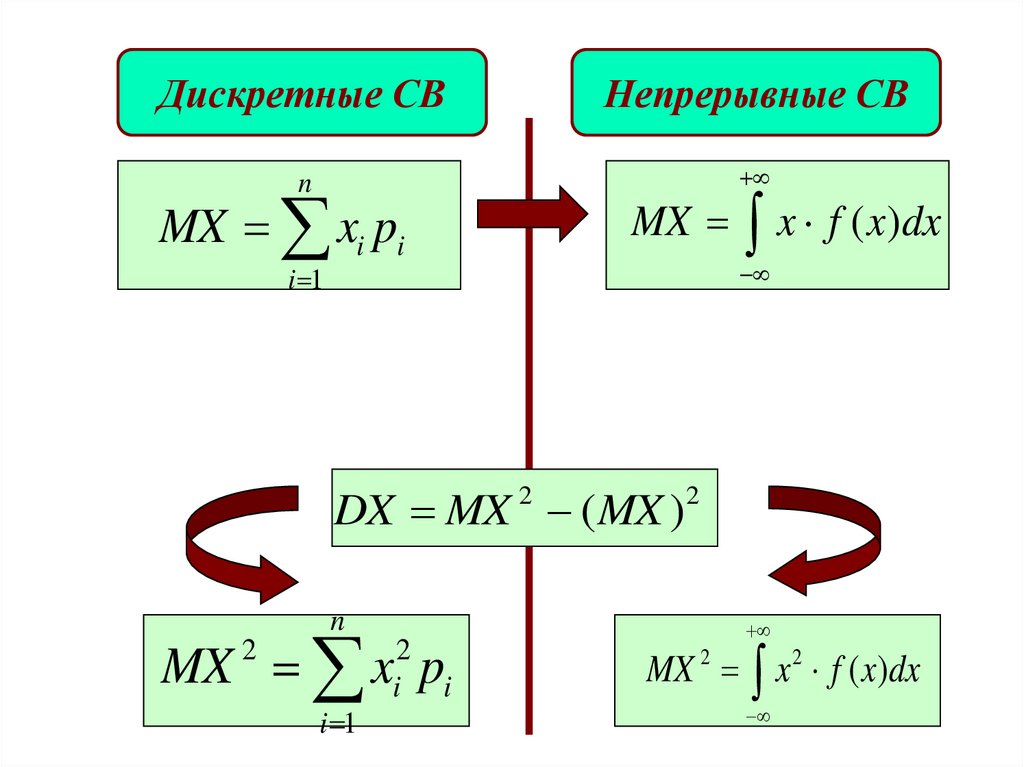
Дискретные СВНепрерывные СВ
n
MX xi pi
MX
i 1
DX MX (MX )
2
n
MX x pi
2
i 1
2
i
x f ( x)dx
2
MX 2 x 2 f ( x)dx
4.
Функция распределения непрерывнойслучайной величины задана выражением:
0, x 0
2
F ( x) x , 0 x 1
1, x 1
Найти плотность вероятности,
вероятность попадания на участок [0.25;0.5],
математическое ожидание и дисперсию .
5.
1. Плотность вероятности находится, какпроизводная от функции распределения:
0, x 0
f ( x) F ( x) 2 x, 0 x 1
0, x 1
6.
Вычисление вероятности попадания назаданный участок может быть произведено
двумя способами: с помощью функции
распределения и с помощью плотности
вероятности.
1 способ.
Используем формулу нахождения вероятности
через функцию распределения:
2.
p(0.25 x 0.5) F (0.5) F (0.25)
0.5 0.25 0.1875
2
2
7.
2 способ.Используем формулу нахождения вероятности
через плотность вероятности:
0.5
p(0.25 X 0.5)
2 xdx x
2 0.5
0.25
0.1875
0.25
4. Находим математическое ожидание:
MX
1
x f ( x)dx
2x
MX x 2 xdx
3
0
3 1
0
2
3
8.
5. Находим дисперсию:DX MX (MX )
2
2
MX x f ( x)dx
2
2
4 1
1
x
MX x 2 xdx
2
0
2
2
0
1
2
Тогда
2
1 2
1
DX
2 3
9
9.
Ежедневная прибыль фирмы является случайнойвеличиной с плотностью вероятностей вида :
a(5 x), x 0;5
f ( x)
x 0;5
0,
Найти параметр а, математическое
ожидание, среднеквадратичное
отклонение. Вероятность того, что прибыль
не превысит 3 ден.ед.





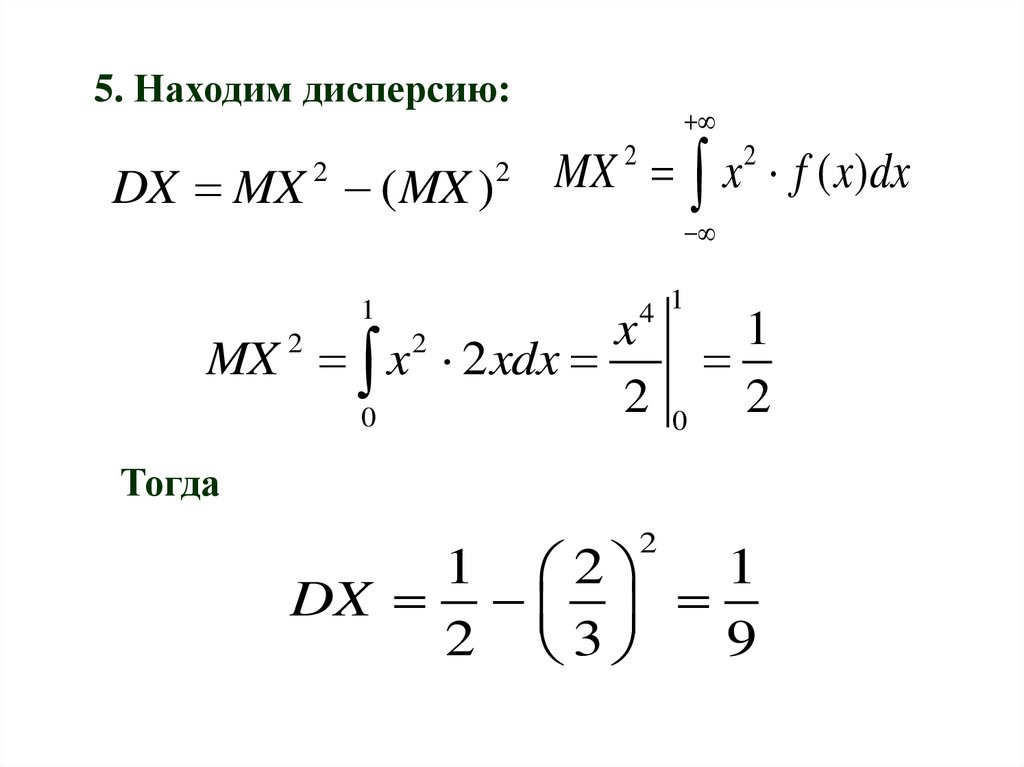

 Математика
Математика