Похожие презентации:
Тригонометрические функции острого угла
1. Синус и косинус острого угла
Синусом острого угла прямоугольного треугольниканазывается отношение противолежащего к этому углу
катета к гипотенузе. Синус угла А обозначается sin A.
Косинусом острого угла прямоугольного треугольника
называется отношение прилежащего к этому углу катета к
гипотенузе. Косинус угла А обозначается cos A.
По определению,
BC
AC
sin A
, cos A
.
AB
AB
2. Тангенс и котангенс острого угла
Тангенсом острого угла прямоугольного треугольниканазывается отношение противолежащего к этому углу
катета к прилежащему.Тангенс угла А обозначается tg A.
Котангенсом острого угла прямоугольного треугольника
называется отношение прилежащего к этому углу катета к
противолежащему. Котангенс угла А обозначается сtg A.
По определению,
BC
AC
tgA
, ctgA
.
AC
BC
3. Тригонометрические функции
Синус, косинус, тангенс и котангенс называюттригонометрическими функциями острого угла.
Из определения тригонометрических функций следует:
1) катет прямоугольного треугольника равен
гипотенузы на синус противолежащего угла;
произведению
2) катет прямоугольного треугольника
гипотенузы на косинус прилежащего угла;
произведению
равен
3) катет прямоугольного треугольника равен произведению второго
катета на тангенс противолежащего угла;
4) катет прямоугольного треугольника равен произведению второго
катета на котангенс прилежащего угла.
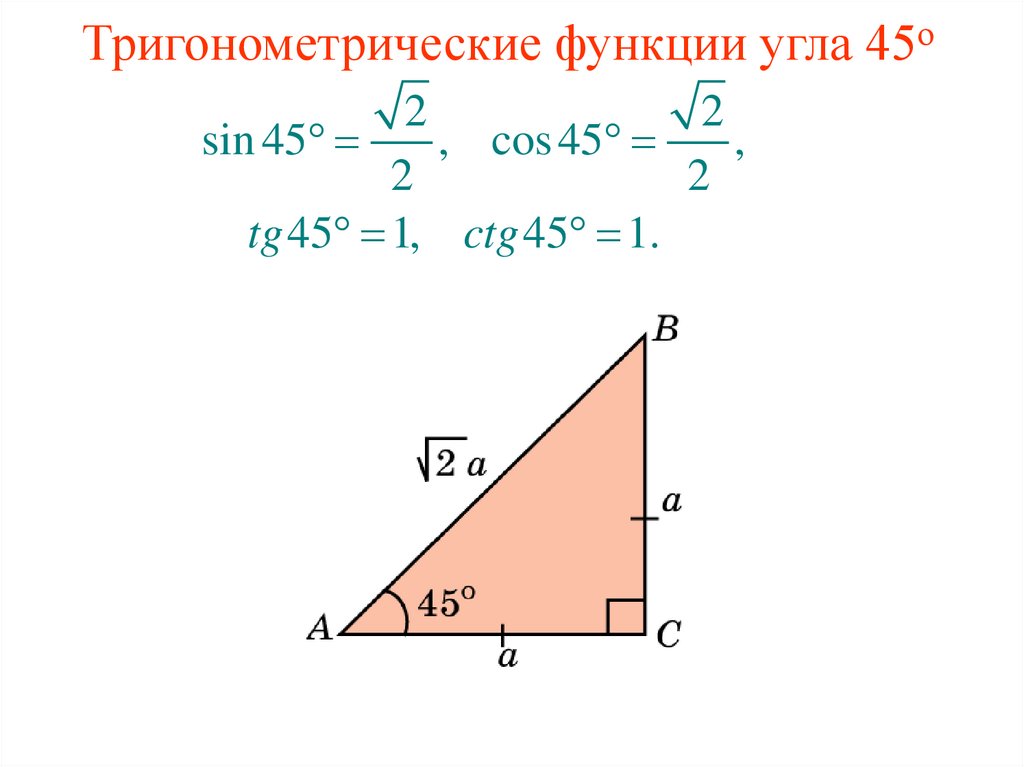
4. Тригонометрические функции угла 45о
22
sin 45
, cos 45
,
2
2
tg 45 1, ctg 45 1.
5. Тригонометрические функции угла 30о
13
sin 30 , cos30
,
2
2
3
tg 30
, ctg 30 3.
3
6. Вопрос 1
Что называется синусомпрямоугольного треугольника?
острого
угла
Ответ: Синусом острого угла прямоугольного
треугольника называется отношение
противолежащего к этому углу катета к
гипотенузе.
7. Вопрос 2
Как обозначается синус угла A?Ответ: Синус угла А обозначается sin A.
8. Вопрос 3
Что называется косинусомпрямоугольного треугольника?
острого
угла
Ответ: Косинусом острого угла прямоугольного
треугольника называется отношение прилежащего
к этому углу катета к гипотенузе.
9. Вопрос 4
Как обозначается косинус угла A?Ответ: Косинус угла А обозначается cos A.
10. Вопрос 5
Что называется тангенсомпрямоугольного треугольника?
острого
угла
Ответ: Тангенсом острого угла прямоугольного
треугольника называется отношение
противолежащего к этому углу катета к
прилежащему.
11. Вопрос 6
Как обозначается тангенс угла A?Ответ: Тангенс угла А обозначается tg A.
12. Вопрос 7
Что называется котангенсомпрямоугольного треугольника?
острого
угла
Ответ: Котангенсом острого угла
прямоугольного треугольника называется
отношение прилежащего к этому углу катета к
противолежащему.
13. Вопрос 8
Как обозначается котангенс угла A?Ответ: Котангенс угла А обозначается ctg A.
14. Вопрос 9
Что называется тригонометрическимифункциями острого угла?
Ответ: Тригонометрическими функциями острого
угла называются синус, косинус, тангенс и
котангенс.
15. Вопрос 10
Чему равен катет, лежащий против угла в 30о?Ответ: Катет, лежащий против угла в 30о равен
половине гипотенузы.
16. Упражнение 1
На клетчатой бумаге изобразите угол, тангенскоторого равен: а) 1; б) 0,5; в) 2; г) 3.
Ответ:
17. Упражнение 2
От луча OA отложите угол, тангенс которогоравен: а) 1/2; б) 1/3; в) 2.
Ответ:
18. Упражнение 3
Найдите значения тригонометрических функцийугла в 60о.
3
1
Ответ: sin 60
, cos60 ,
2
2
3
tg 60 3, ctg 60
.
3
19. Упражнение 4
Может ли синус (косинус) угла быть равен 2 ?Ответ: Нет, значения синуса и косинуса
меньше единицы.
20. Упражнение 5
Катеты прямоугольного треугольника равны 12см и 5 см. Найдите все тригонометрические
функции его меньшего угла A.
Ответ:
5
12
sin A , cos A ,
13
13
5
12
tgA , ctgA .
12
5
21. Упражнение 6
Высота,проведенная
к
основанию
равнобедренного треугольника, равна 8 см,
основание равно 12 см. Найдите синус и косинус
угла A при основании треугольника.
4
3
Ответ: sin A , cos A .
5
5
22. Упражнение 7
Основание равнобедренного треугольника равно24 см, а угол при основании 30о. Найдите боковую
сторону.
Ответ: 8 3 см.
23. Упражнение 8
В треугольнике АВС угол А равен 60о, АВ = 3 см,ВС = 4 см. Найдите АС.
3 37
Ответ:
.
2
Решение. Проведем высоту
BH.
3 3
Тогда BH =
, AH = 1,5.
2
37
CH = .
2
3 37
Следовательно, АС =
.
2
24. Упражнение 9
У прямоугольного треугольника один катет равен8 см, а синус противолежащего ему угла равен
0,8. Найдите гипотенузу и второй катет.
Ответ: 10 см и 6 см.
25. Упражнение 10
Диагональ прямоугольника в два раза большеодной из его сторон. Найдите угол между
диагоналями.
Ответ: 60о.
26. Упражнение 11
В прямоугольном треугольнике проекциикатетов на гипотенузу равны 1 и 3. Найдите его
острые углы.
Решение. Проведем высоту CH.
Имеем CH = AH tg A = tg A.
С другой стороны,
CH = BH/tg A = 3/tg A.
Следовательно, tg A = 3/tg A.
Решая это уравнение находим
Ответ:
60о,
30о.
tg A =
60о.
3 и, значит, угол A равен
27. Упражнение 12
Найдите углы ромба, если его диагоналиравны 2 3 и 2.
Решение. AO = 3 , OD
= 1. Так как диагонали
ромба перпендикулярны,
то угол OAD равен 30о и,
следовательно, углы
ромба равны 60о и 120о.
Ответ: 60о, 120о.
28. Упражнение 13
Катеты прямоугольного треугольника равны а иb. Найдите высоту h, опущенную на гипотенузу.
h
a 2 h2
Решение. Имеем sin A =
.
b
a
ab
Откуда h
.
2
2
a b
Ответ:
ab
a2 b
.
2
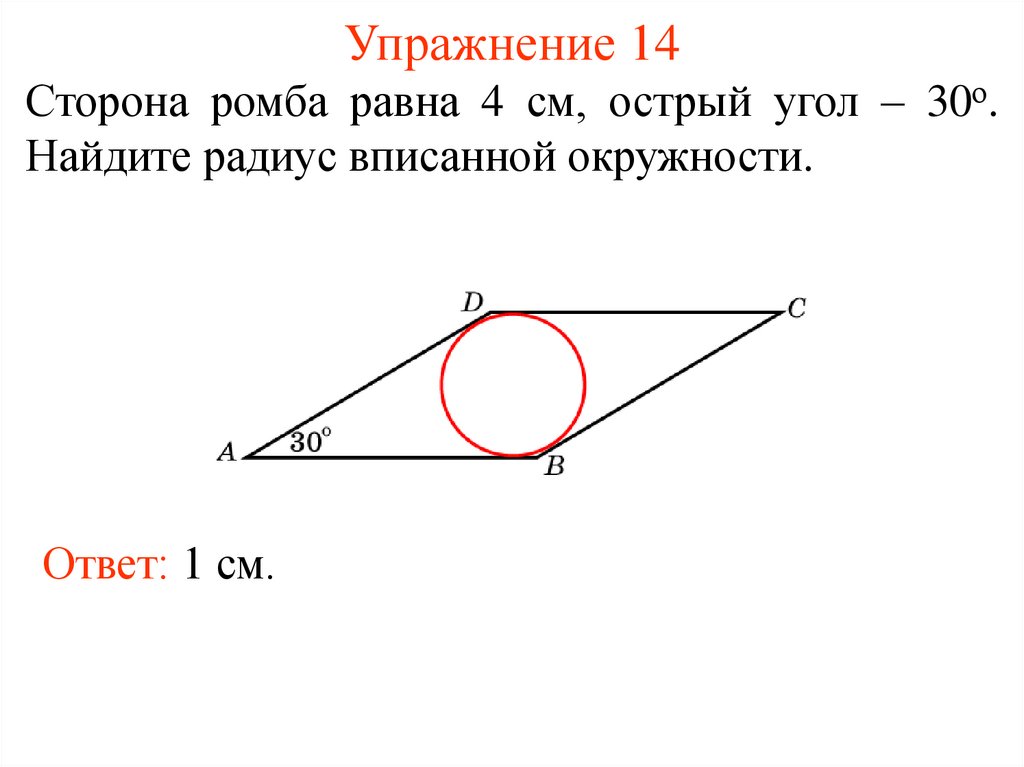
29. Упражнение 14
Сторона ромба равна 4 см, острый угол – 30о.Найдите радиус вписанной окружности.
Ответ: 1 см.
30. Упражнение 15
Острый угол ромба равен 30о. Радиус вписаннойокружности равен 2. Найдите сторону ромба.
Ответ: 8.
31. Упражнение 16*
Найдите синус угла в 18о.Решение. Рассмотрим золотой
треугольник ABC, у которого угол
C равен 36о. Проведем высоту CH.
1
5
Если AC = 1, то AH =
.
4
Следовательно, sin
1 5
Ответ:
.
4
18о
1 5
=
.
4
32. Упражнение 17*
Найдите синус угла в 54о.Решение. Рассмотрим
золотой треугольник ABC,
у которого угол C равен
108о. Проведем высоту
CH. Если AC = 1, то
1 5
AH = 4 .
1 5
Ответ:
.
4
Следовательно,
sin
54о
1 5
=
.
4
33. Упражнение 18*
Найдите косинус угла в 18о.Ответ:
5 5
.
8
34. Упражнение 19*
Найдите косинус угла в 54о.10 2 5
Ответ:
.
4
































 Математика
Математика








