Похожие презентации:
Полярные координаты
1. Полярные координаты
Пусть на плоскости задана координатная прямая с выделеннойточкой О и единичным отрезком ОЕ. Эта прямая в данном случае
будет называться полярной осью. Точка O называется полюсом.
Полярными координатами точки А на плоскости с заданной
полярной осью называется пара (r, ), где r - расстояние от точки А
до точки О, - угол между полярной осью и вектором
OA ,
отсчитываемый в направлении против часовой стрелки, если > 0
и по часовой стрелке, если < 0.
При этом первая координата r
называется полярным радиусом, а вторая
- полярным углом. Полярный угол
можно задавать в градусах или радианах.
2. Полярные координаты
Если на плоскости задана декартова система координат, то обычноза полюс принимается начало координат и за полярную ось – ось
Ox. В этом случае каждой точке плоскости с декартовыми
координатами (x, y) можно сопоставить полярные координаты (r, ).
При этом декартовы координаты выражаются через полярные по
формулам:
x r cos ,
y r sin .
Наоборот,
полярные
координаты
выражаются через декартовы по
формулам:
r x2 y 2 ,
cos
x
x y
2
2
, sin
y
x y
2
2
.
3. Упражнение 1
Для следующих точек с заданными полярнымикоординатами найдите их декартовы координаты:
а) (1, 3 ); б) (2, - 4 ).
Ответ: а)
1
(2
,
3
2
);
б) (
2
,-
2
).
4. Упражнение 2
Для следующих точек с заданными декартовымикоординатами найдите их полярные координаты: а)
( , 2 );2б) (-10, 0); в) (1, - );3 г) (- , 31).
Ответ: а) (2, ); б) (10, ); в) (2, - ); г) (2, 5 ).
4
3
6
5. Окружность
Окружность радиуса R с центром в точке О задаетсяуравнением r R.
Действительно,
окружность
является геометрическим местом
точек, удаленных от точки О на
расстояние R. Все такие точки
удовлетворяют равенству r = R.
При
этом,
если
угол
увеличивается, то соответствующая
точка на окружности движется в
направлении
против
часовой
стрелки, описывая круги. Если же
угол
уменьшается,
то
соответствующая точка описывает
круги в направлении по часовой
стрелке.
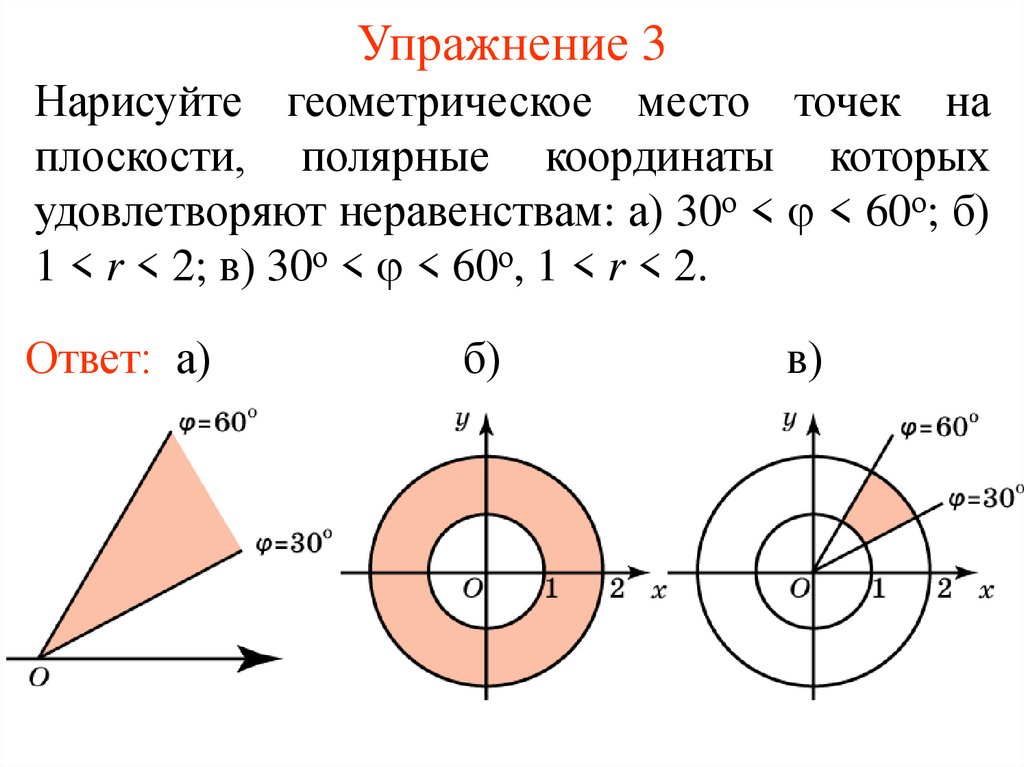
6. Упражнение 3
Нарисуйте геометрическое место точек наплоскости, полярные координаты которых
удовлетворяют неравенствам: а) 30о < < 60о; б)
1 < r < 2; в) 30о < < 60о, 1 < r < 2.
Ответ: а)
б)
в)
7. Спираль Архимеда
Спираль Архимеда - кривая, задаваемая уравнением r= a , где a - некоторое фиксированное число, угол
задается в радианах.
Геометрическим
свойством,
характеризующим
спираль
Архимеда, является постоянство
расстояний
между
соседними
витками, каждое из них равно 2πa.
Действительно,
если
угол
увеличивается на 2π, т.е. точка делает
один, то радиус увеличивается на
2πa, что и составляет расстояние
между соседними витками.
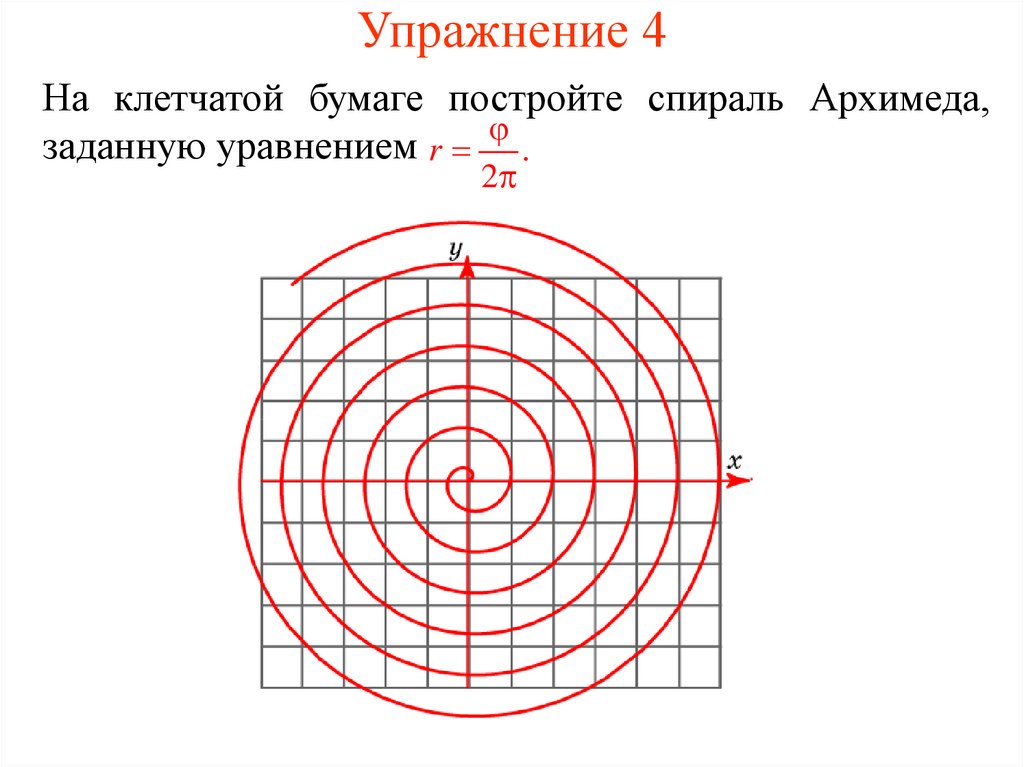
8. Упражнение 4
На клетчатой бумаге постройте спираль Архимеда,заданную уравнением r .
2
9. Упражнение 5
Нарисуйте спираль Архимеда, заданнуюуравнением r = a , a < 0.
Ответ:
10. Упражнение 6
Человек идет с постоянной скоростью вдольрадиуса вращающейся карусели. Какой будет его
траектория относительно земли?
Ответ: Спираль Архимеда.
11. Трилистник
Трилистник – кривая, задаваемая уравнением r = sin 3 .Для построения этой кривой сначала заметим, что, поскольку
радиус неотрицателен, должно выполняться неравенство sin 3 0,
решая которое находим область допустимых значений углов :
0о 60о; 120о 180о; 240о 300о.
Если угол изменяется от нуля до 30о,
то радиус r изменяется от нуля до
единицы. Если угол изменяется от
30о до 60о, то радиус изменяется от
единицы до нуля. Таким образом, при
изменении угла от 0о до 60о точка
описывает кривую, похожую на
очертания лепестка. Такие же
лепестки получаются когда угол
изменяется в пределах от 120о до 180о
и от 240о до 300о.
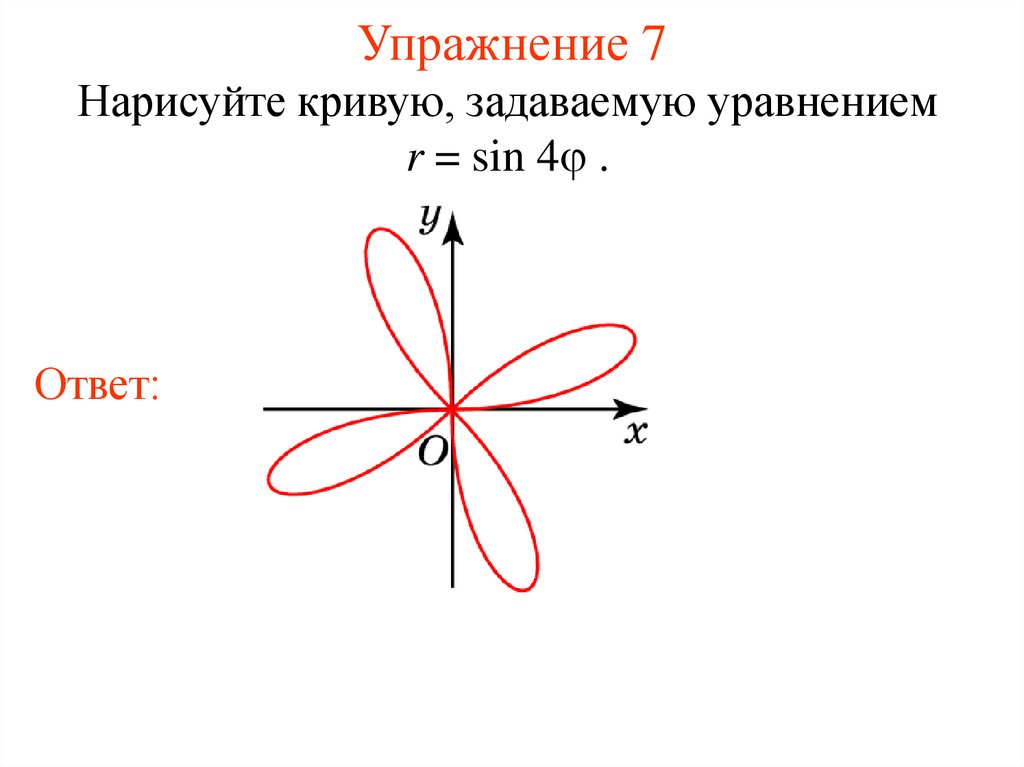
12. Упражнение 7
Нарисуйте кривую, задаваемую уравнениемr = sin 4 .
Ответ:
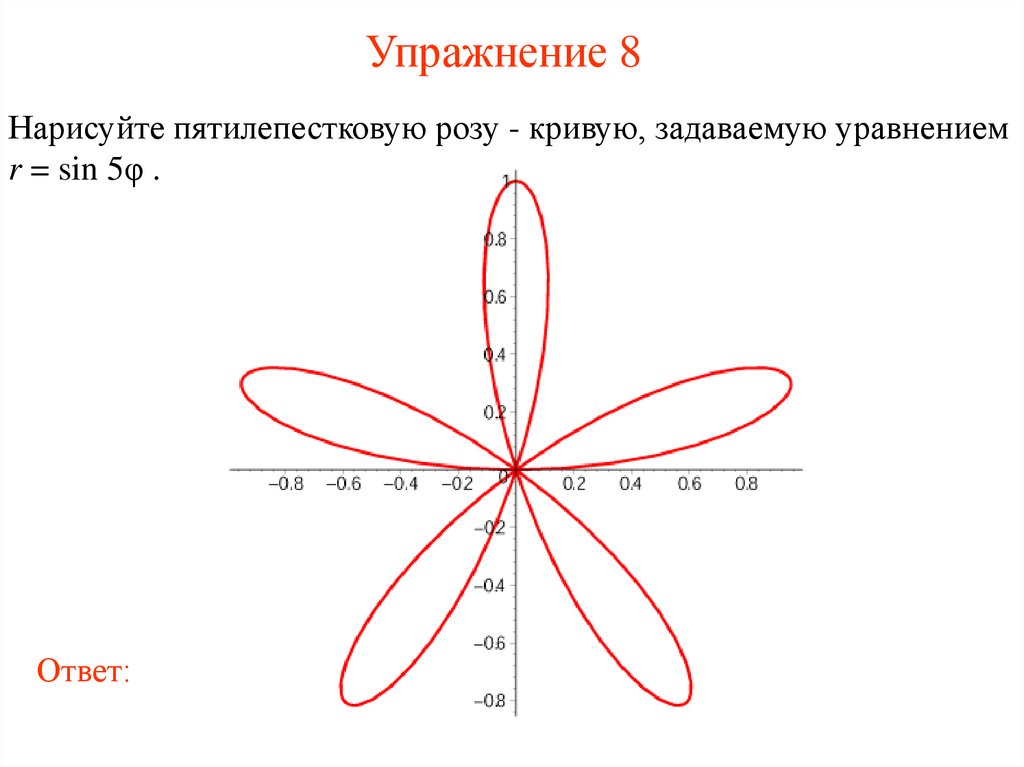
13. Упражнение 8
Нарисуйте пятилепестковую розу - кривую, задаваемую уравнениемr = sin 5φ .
Ответ:
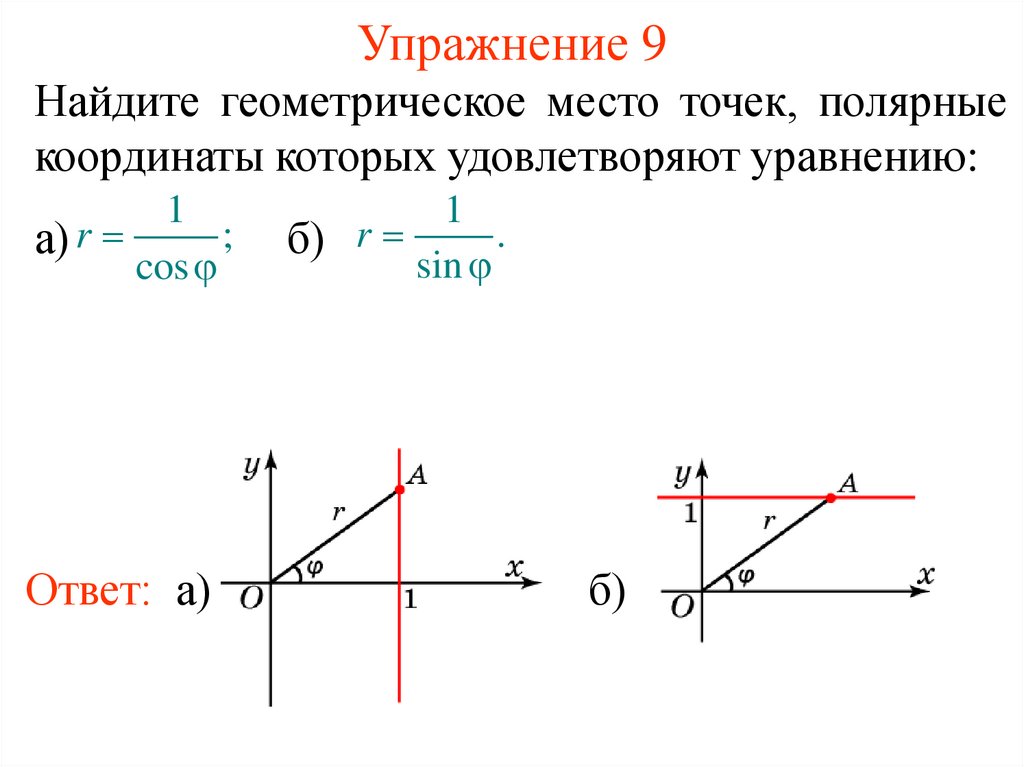
14. Упражнение 9
Найдите геометрическое место точек, полярныекоординаты которых удовлетворяют уравнению:
1
;
а) r
cos
Ответ: а)
1
.
б) r
sin
б)
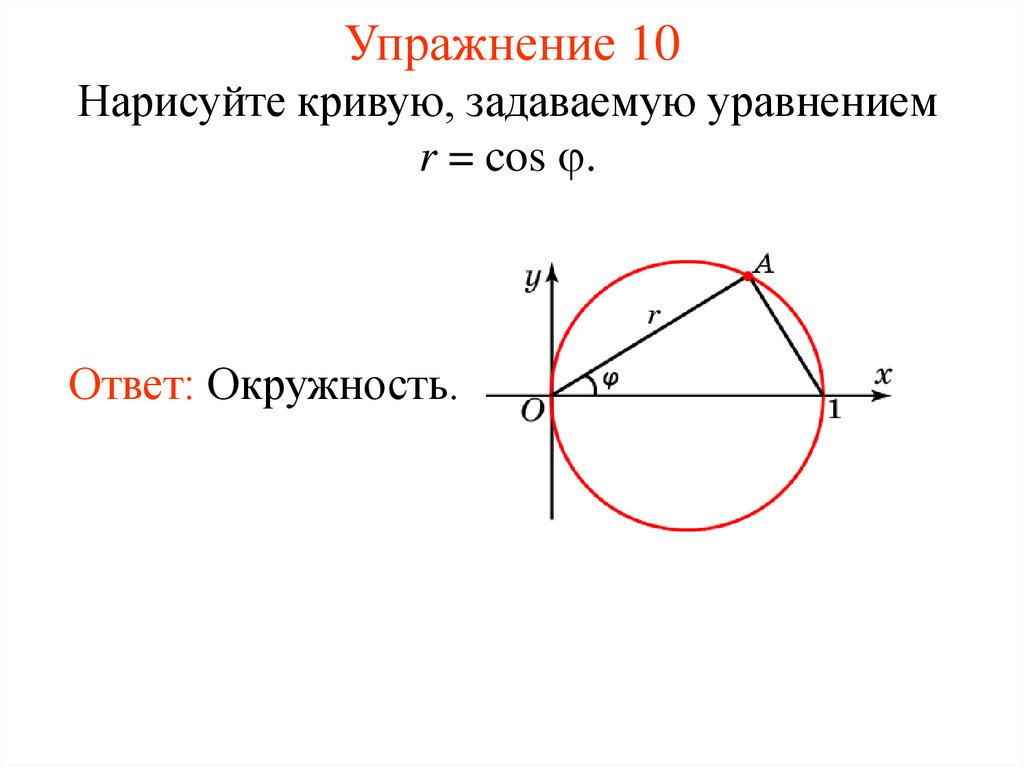
15. Упражнение 10
Нарисуйте кривую, задаваемую уравнениемr = cos .
Ответ: Окружность.
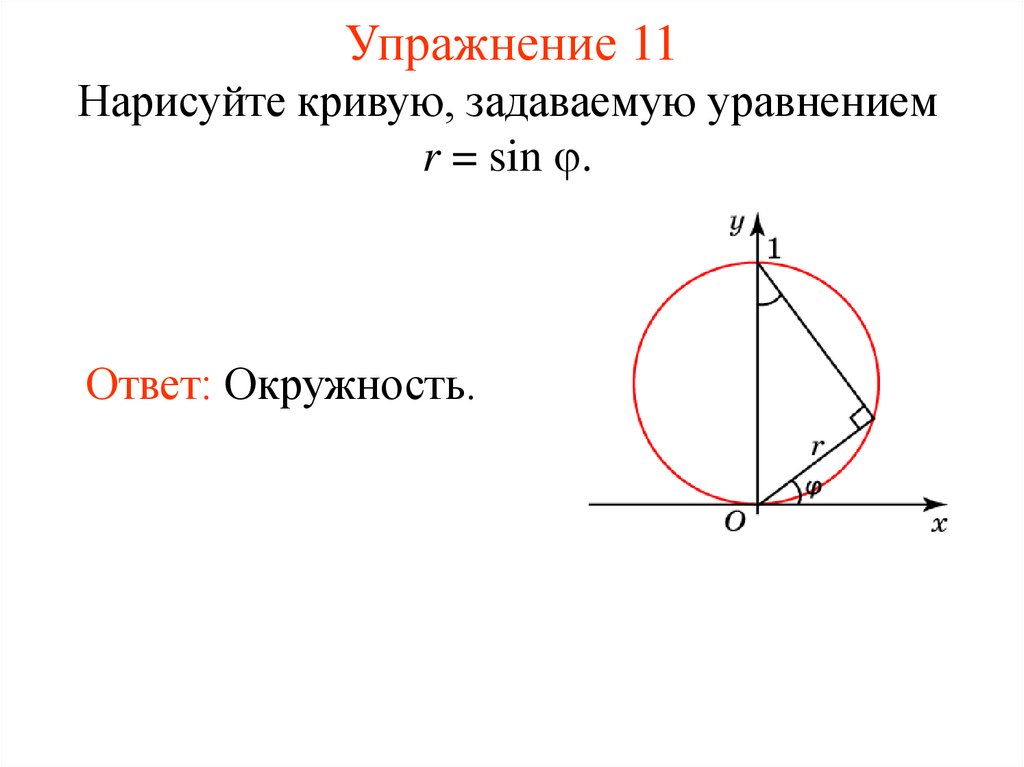
16. Упражнение 11
Нарисуйте кривую, задаваемую уравнениемr = sin .
Ответ: Окружность.
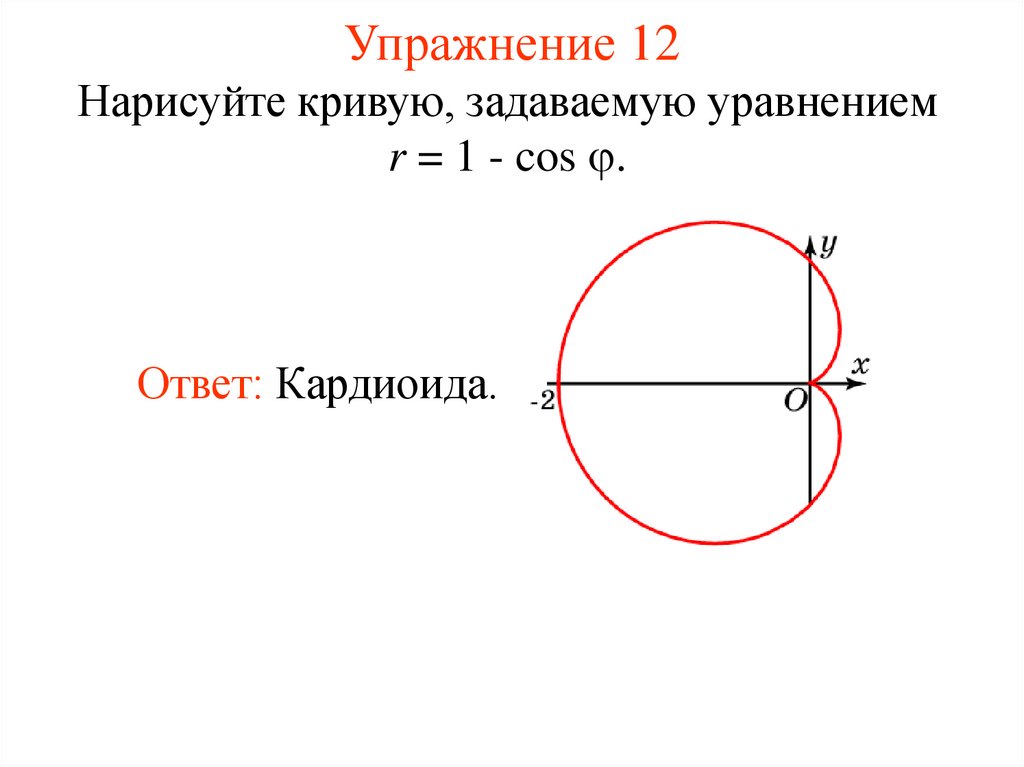
17. Упражнение 12
Нарисуйте кривую, задаваемую уравнениемr = 1 - cos .
Ответ: Кардиоида.
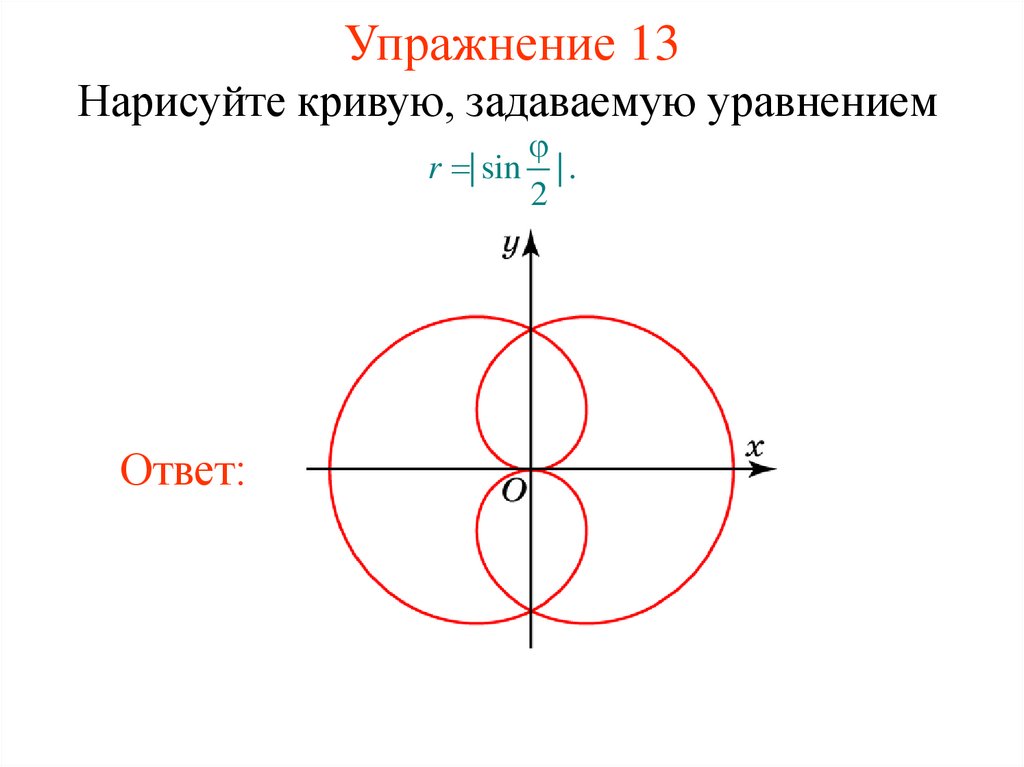
18. Упражнение 13
Нарисуйте кривую, задаваемую уравнениемr | sin | .
2
Ответ:
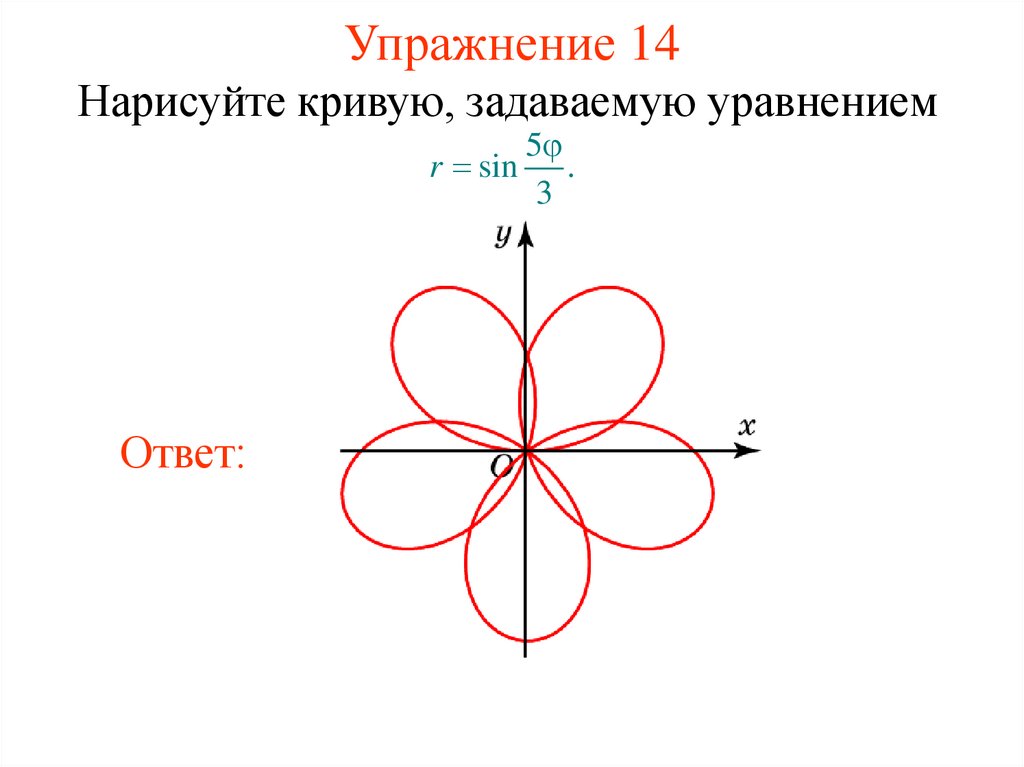
19. Упражнение 14
Нарисуйте кривую, задаваемую уравнением5
r sin .
3
Ответ:
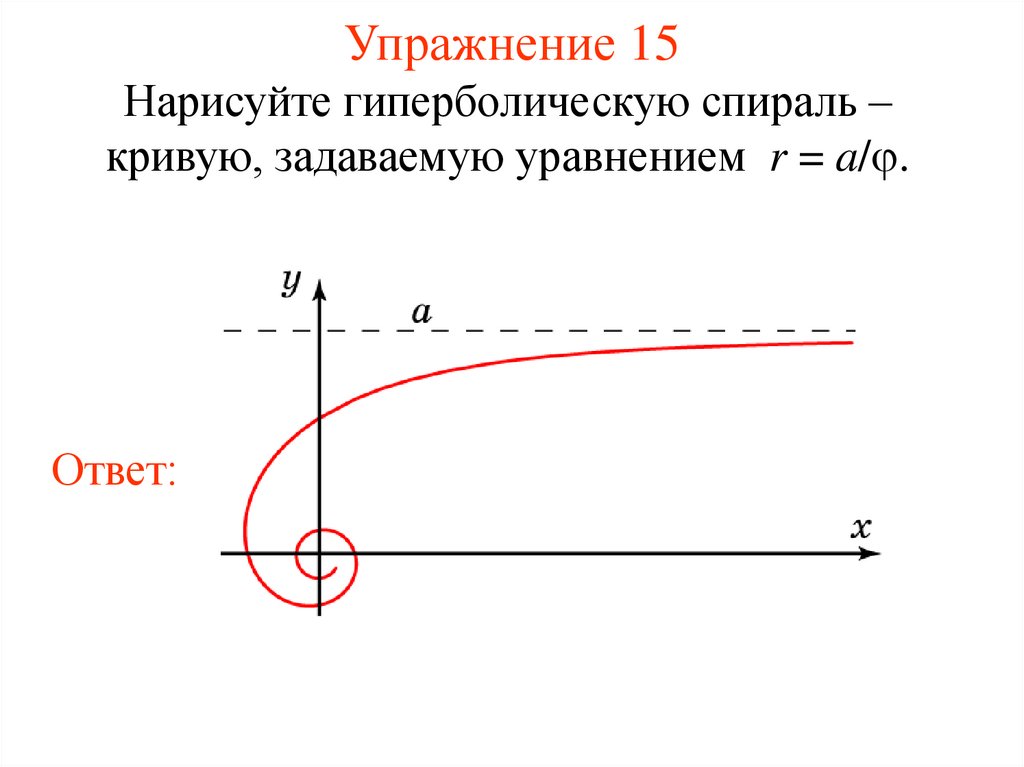
20. Упражнение 15
Нарисуйте гиперболическую спираль –кривую, задаваемую уравнением r = a/ .
Ответ:
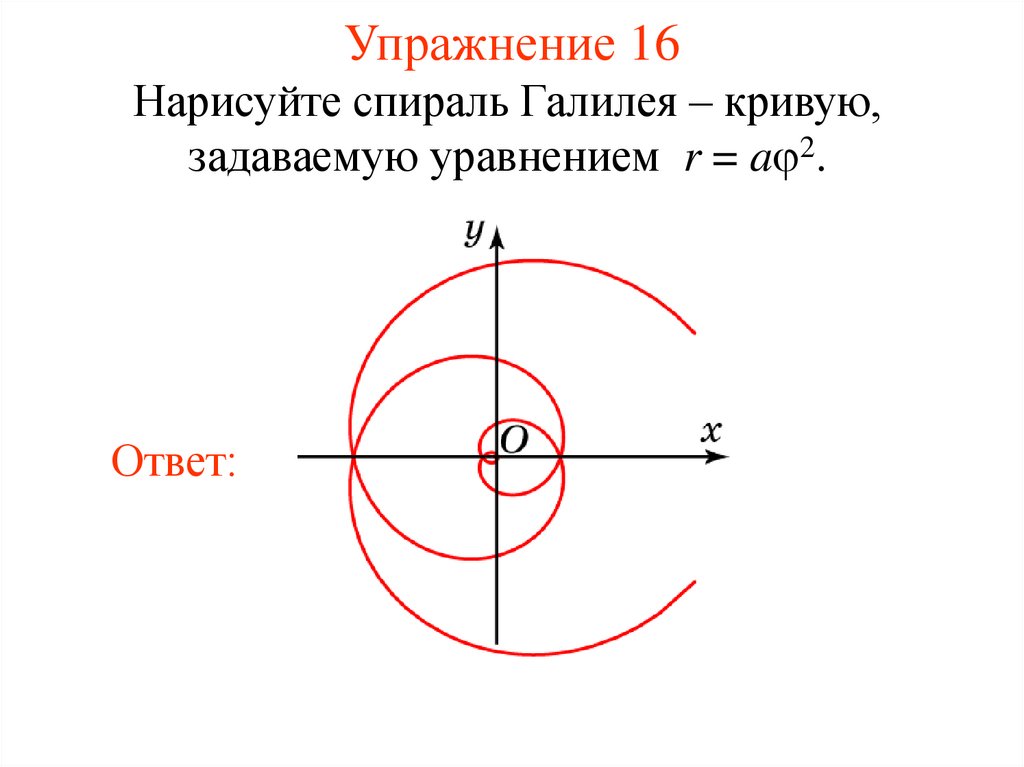
21. Упражнение 16
Нарисуйте спираль Галилея – кривую,задаваемую уравнением r = a 2.
Ответ:
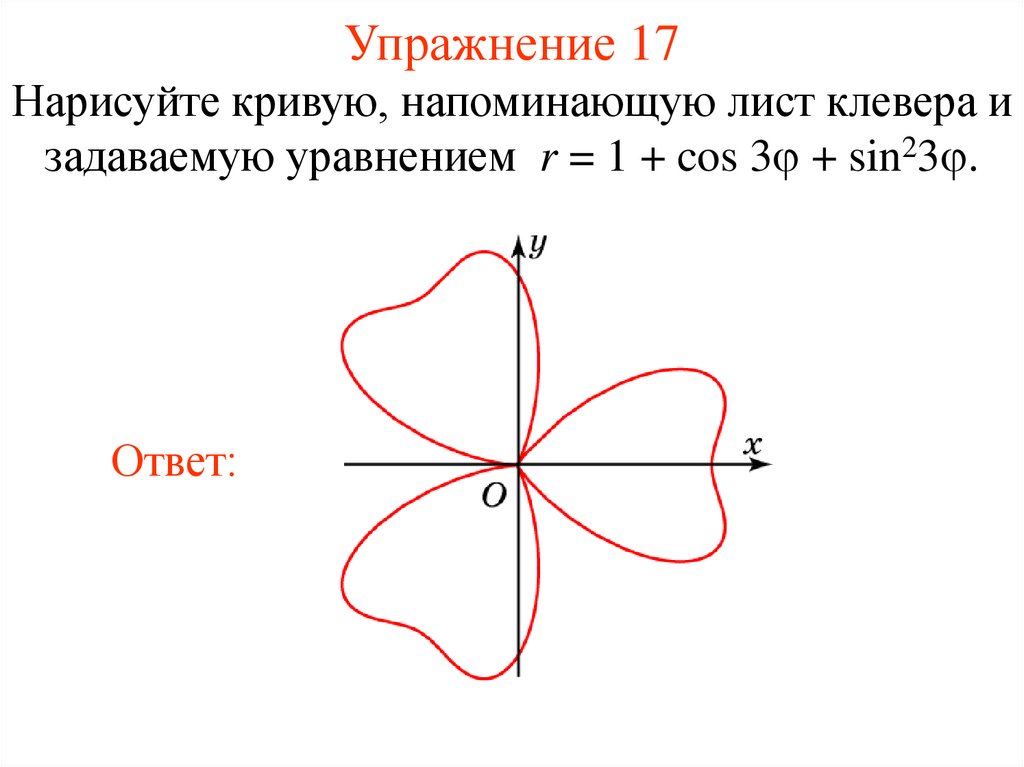
22. Упражнение 17
Нарисуйте кривую, напоминающую лист клевера изадаваемую уравнением r = 1 + cos 3 + sin23 .
Ответ:









 Математика
Математика








