Полярная система координат

1. ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ

Сибирский государственный университет путей сообщения
О. И. Хаустова
ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ
Лекции по дисциплине:
Математика
Новосибирск - 2010

2. Содержание:

ВВЕДЕНИЕ
Цель
Задачи
Полярная система координат на плоскости
Примеры построения точек в полярной системе координат
Взаимосвязь прямоугольной декартовой и полярной систем координат
Построение графиков функций в полярной системе координат
Некоторые линий в полярной системе координат
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
Далее
© Хаустова О.И.
2

3. ВВЕДЕНИЕ

Положение любой точки в пространстве (в частности,
на плоскости) может быть определено при помощи
той или иной системы координат.
Наиболее употребительны - декартовы прямоугольные
системы координат, изучению которых посвящены
многие разделы школьного курса математики.
Зачастую на плоскости задают полярные системы
координат, а в пространстве - цилиндрические или
сферические системы координат.
Применение полярных координат позволяет
существенно упростить решение многих
теоретических задач, а также находит широкое
практическое приложение.
Далее
© Хаустова О.И.
3

4. Цель:

изучить основные понятия полярной системы
координат, методы построения кривых в
полярной системе координат, возможности
перехода от полярной системы координат к
прямоугольной декартовой, и обратно.
Далее
© Хаустова О.И.
4

5. Задачи:

изучить основные понятия полярной системы
координат;
развить умения и навыки по построению линий
в полярной системе координат;
вывести формулы взаимосвязи полярной и
прямоугольной декартовой систем координат;
изучить способы задания некоторых линий в
полярной системе координат.
Далее
© Хаустова О.И.
5

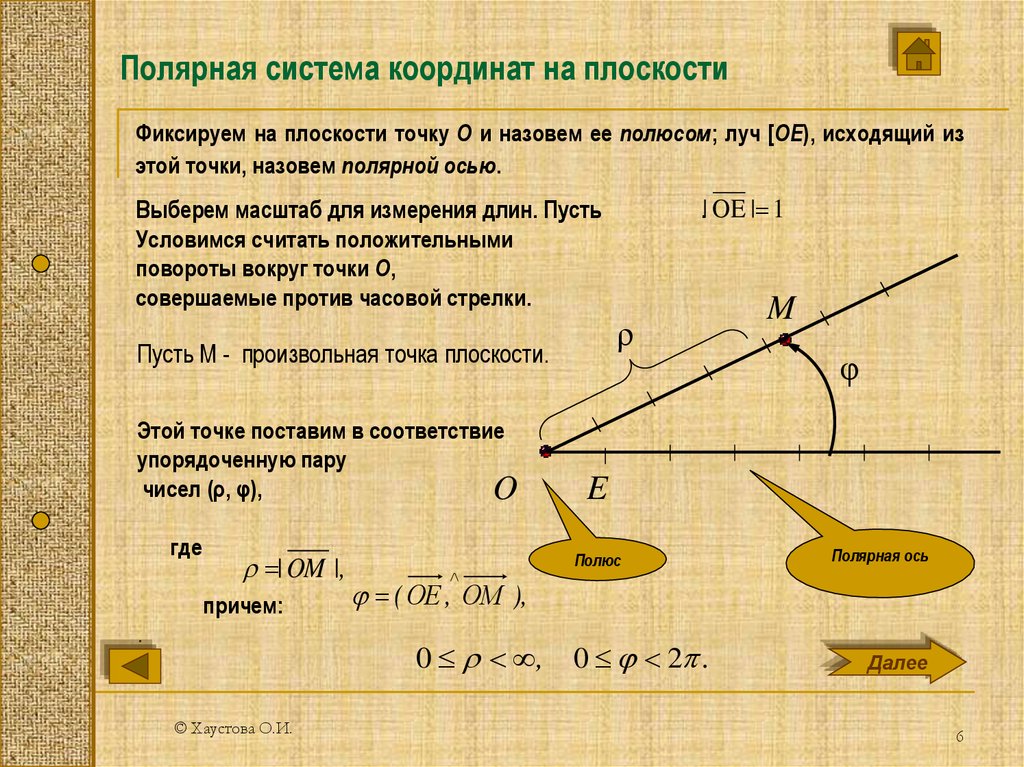
6. Полярная система координат на плоскости

Фиксируем на плоскости точку О и назовем ее полюсом; луч [ОЕ), исходящий из
этой точки, назовем полярной осью.
.| OE | 1
Выберем масштаб для измерения длин. Пусть
Условимся считать положительными
повороты вокруг точки О,
совершаемые против часовой стрелки.
ρ
Пусть М - произвольная точка плоскости.
Этой точке поставим в соответствие
упорядоченную пару
чисел (ρ, φ),
O
где
| OM |,
причем:
.
φ
E
Полюс
Полярная ось
( ОЕ , ОМ ),
0 , 0 2 .
© Хаустова О.И.
M
Далее
6

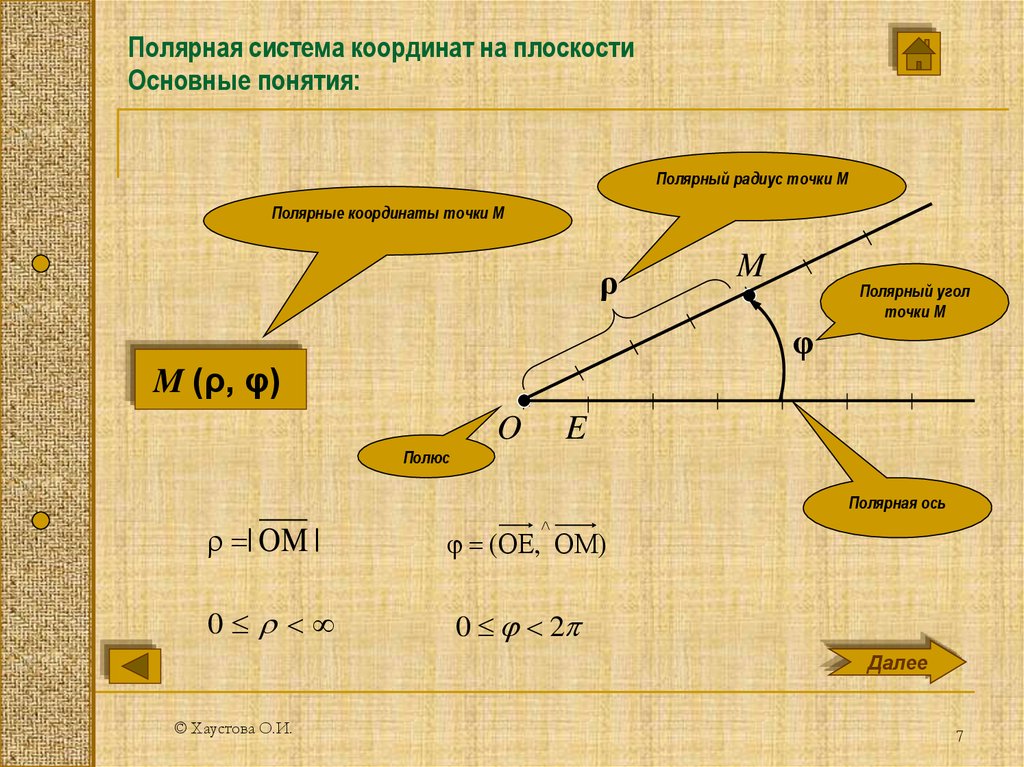
7. Полярная система координат на плоскости Основные понятия:

Полярный радиус точки М
Полярные координаты точки М
ρ
M
Полярный угол
точки М
φ
M (ρ, φ)
O
E
Полюс
Полярная ось
| OM |
0
(ОЕ, ОМ)
0 2
Далее
© Хаустова О.И.
7

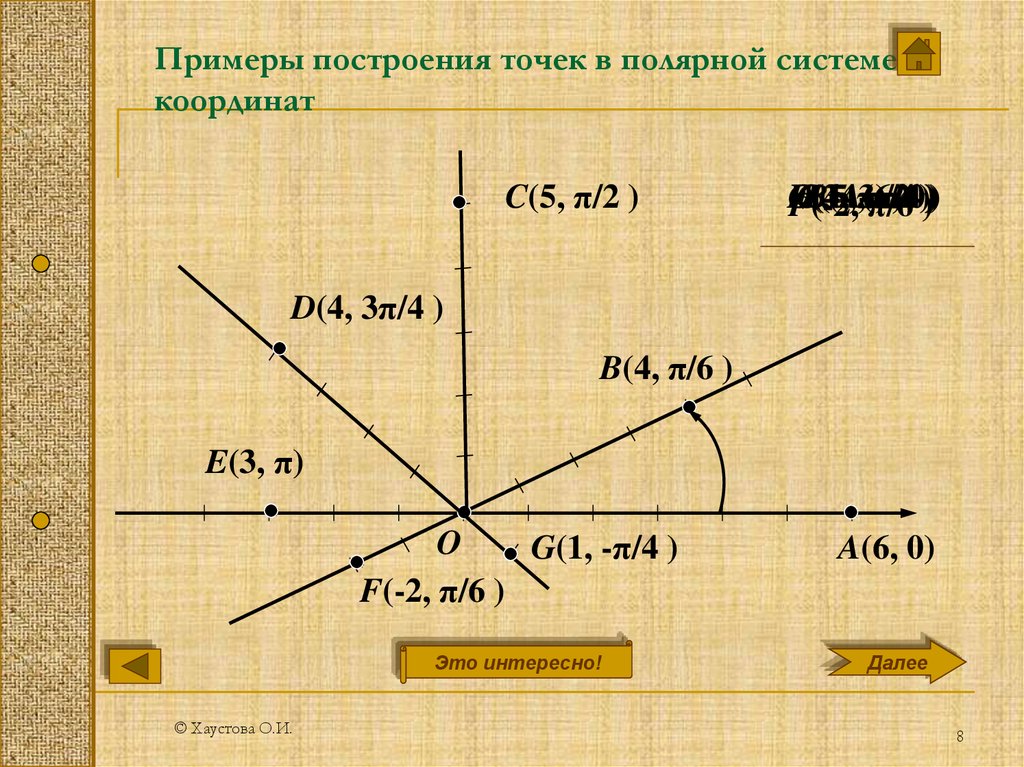
8.

Примеры построения точек в полярной системе
координат
C(5, π/2 )
E(3,
D(4,
G(1,
C(5,
B(4,
A(6,
π)
3π/4
-π/4
π/2
π/60)
))))
F(-2,
π/6
D(4, 3π/4 )
B(4, π/6 )
E(3, π)
O
G(1, -π/4 )
F(-2, π/6 )
Это интересно!
© Хаустова О.И.
A(6, 0)
Далее
8

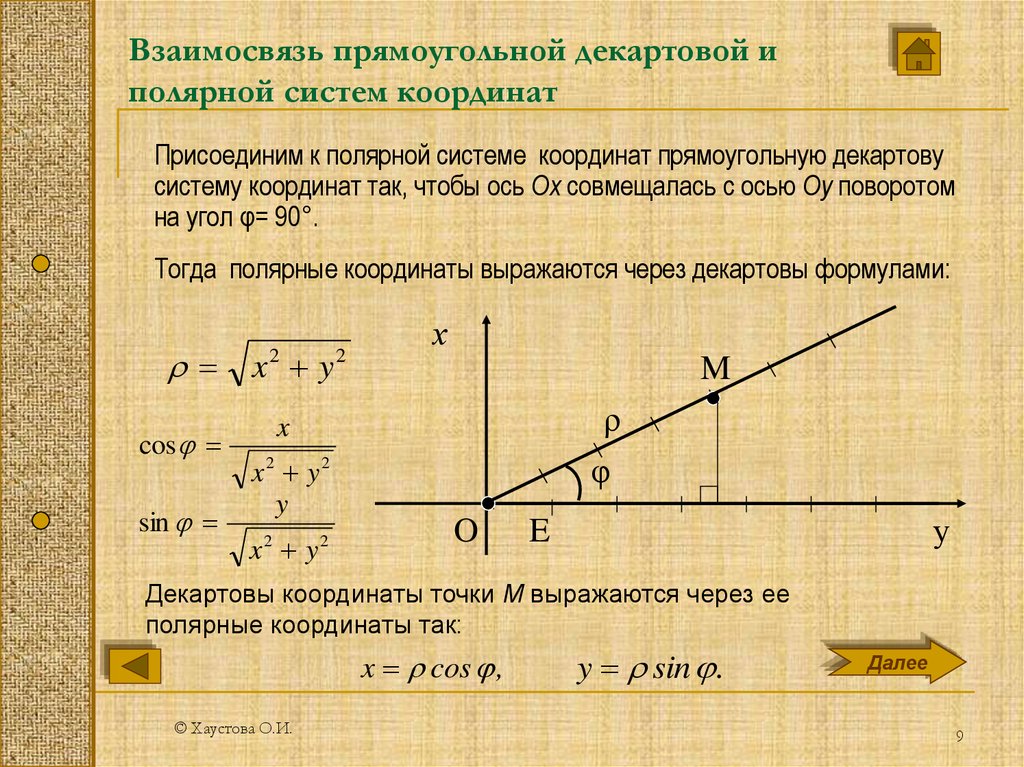
9. Взаимосвязь прямоугольной декартовой и полярной систем координат

Присоединим к полярной системе координат прямоугольную декартову
систему координат так, чтобы ось Ох совмещалась с осью Оу поворотом
на угол φ= 90°.
Тогда полярные координаты выражаются через декартовы формулами:
x y
2
cos
sin
2
х
M
ρ
φ
x
x2 y2
y
x2 y 2
O
у
E
Декартовы координаты точки М выражаются через ее
полярные координаты так:
x cos ,
© Хаустова О.И.
y sin .
Далее
9

10. Построение графиков функций в полярной системе координат

Постройте кривую, заданную уравнением =sin .
1) подготовим таблицу значений и :
0
/6
/4
/3
/2
2 /3
5 /6
7 /6
0
1/2
√2/2
√3/2
1
√3/2
1/2
0
- √3/2
2) выберем полюс О, проведем полярный радиус горизонтально.
/2
2 /3
Это соответствует =0.
Все остальные углы
будем откладывать от него
против часовой стрелки.
/3
/4
/6
5 /6
7 /6
ρ
O
Далее

11.

3) для каждого выбранного отложим от полюса вычисленные ;
2 /3
/2
/3
/4
/6
5 /6
O
ρ
7 /6
4) для отрицательных значений ( - √3/2) расстояние от полюса
откладывается вдоль противоположного направления ;
5) остальные отрицательные совпадут с имеющимися точками;
Далее
© Хаустова О.И.
11

12.

6) соединяем все точки плавной линией:
2 /3
/2
/3
/4
5 /6
/6
O
7 /6
ρ
Уравнение = sin
Определим аналитически центр и радиус полученной окружности.
Далее
© Хаустова О.И.
12

13.

Линия задана в полярной системе
координат уравнением = sin .
у
х
O
Найдем уравнение этой линии
в прямоугольной декартовой
системе координат с началом
в полюсе и осью Ох,
совпадающей с полярной
осью.
Согласно формулам перехода имеем:
Тогда:
Выделив полный квадрат,
y
получим:
2
2
x y
y
x 2 y 2 , sin
x y
2
2
,
1
1 1
x 2 y 2 - 2 y - 0,
2
4 4
x2 y2 y,
2
1
1
2
2
2
x y - y 0,
x y- .
2
4
Уравнение окружности
x y
2
2
1
1
с центром в точке 0; , радиусом .
2
2
© Хаустова О.И.
Далее
13
.

14.

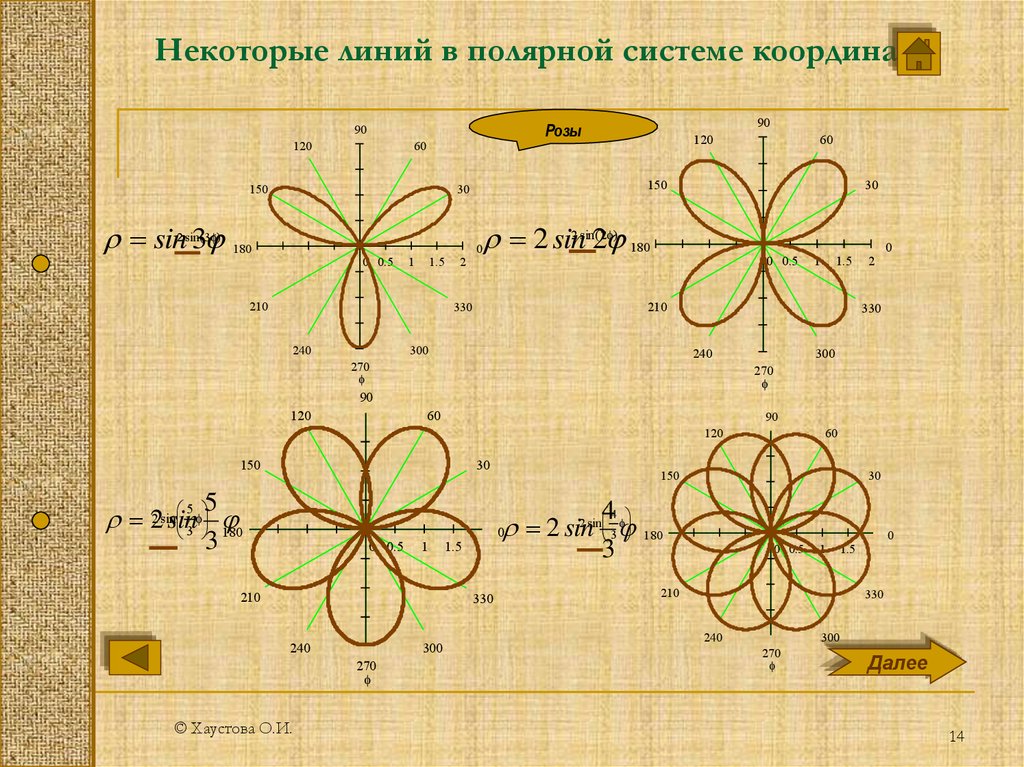
Некоторые линий в полярной системе координат
120
60
150
sin 3
2 sin( 3 )
90
Розы
90
120
150
30
180
0 0.5
1
1.5
210
2
0
30
2 sin2 sin2( 2 ) 180
0 0.5
300
60
90
150
30
5
3
0 0.5
1
210
300
270
© Хаустова О.И.
4 4
3
30
2 sin
2 sin
3
1.5
60
150
0
330
240
0
300
120
5
2
270
90
22 sinsin
3 180
1.5
330
240
270
120
1
210
330
240
60
180
0 0.5
1
210
0
1.5
330
240
300
270
Далее
14

15.

90
90
120
120
60
150
150
30
2 2 180
0 10
20
30
40
210
60
0
30
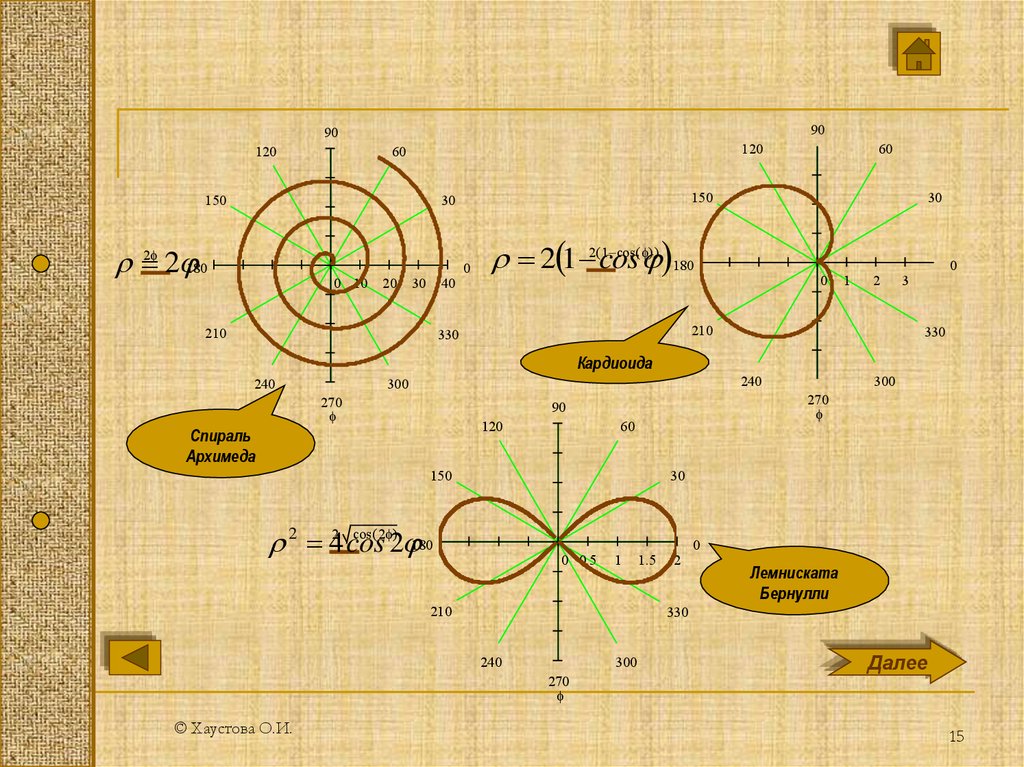
1- cos( ) )
2(1 -2(cos
)180
0
1
2
210
330
0
3
330
Кардиоида
240
240
300
270
270
90
120
Спираль
Архимеда
60
150
30
cos ( 2 )
2 42 cos
2 180
0 0.5
1
210
1.5
2
0
Лемниската
Бернулли
330
240
300
270
© Хаустова О.И.
300
Далее
15

16. ЗАКЛЮЧЕНИЕ

В лекции было дано определение и рассмотрены
основные понятия полярной системы координат,
приводились примеры построения линий в полярной
системе координат, были выведены формулы
взаимосвязи полярной и прямоугольной декартовой
систем координат, а также рассмотрены примеры
задания некоторых линий в полярной системе
координат.
Далее
© Хаустова О.И.
16

17. СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ:

Гусак,
А. А. Справочник по высшей математике [Текст] / А.
А. Гусак, Г. М. Гусак, Е. А. Бричикова. – Мн.:
ТетраСистемс, 1999. – 640 с.
Дмитриева,
А. В. Элективный курс по геометрии
«Инверсия и ее приложения к решению задач»: учебнодидактический комплекс [Текст] / А. В. Дмитриева. –
Новосибирск: Изд. НГПУ, 2005. – 193 с.
Свободная
энциклопедия «Википедия» [Электронный
ресурс] / URL:http://ru.wikipedia.org/wiki/
© Хаустова О.И.
17