Дифференциальные уравнения конвективного теплообмена

1. Проблемы энерго- и ресурсосбережения

Дифференциальные уравнения
конвективного теплообмена

2. Дифференциальное уравнение энергии

Выведем дифференциальное уравнение
температурного поля в движущейся
жидкости.
Допущения:
• Жидкость однородна и изотропна;
• Физические параметры постоянны;
• Энергия деформации мала в сравнении с
изменением внутренней энергии.

3. Дифференциальное уравнение энергии

dQz dz
z
dQx
dz
dQy dy
dQy
0
x
dQx dx dy
dQz
dx
y

4. Дифференциальное уравнение энергии

Формально дифференциальное уравнение энергии будет таким
же как и при отсутствии конвекции:
h
divq qv ,
где
qx q y qz
divq
x y z
(1)

5. Дифференциальное уравнение энергии

Плотность теплового потока при конвективном
теплообмене:
q qтпр qконв
t wh

6. Дифференциальное уравнение энергии

Отсюда проекции плотности теплового потока
на координатные оси:
t
qx wx h;
x
t
q y wy h;
y
t
qz wz h
z

7. Дифференциальное уравнение энергии

Тогда уравнение (1) примет вид:
2t 2t 2t
h
( 2 2 2 )
x y z
h
h
h
(wx wy wz )
z
y
x
wx wy wz
) qv
h(
z
x y
(2)

8. Дифференциальное уравнение энергии

Для несжимаемых жидкостей:
wx wy wz
divw
0
x y
z

9. .

Дифференциальное
уравнение энергии
.
Тогда уравнение (2) примет вид:
h
h
h
h
wx wy wz
x
y
z
t t t qv
( 2 2 2)
x y z
2
.
2
2
(3)

10. .

Дифференциальное
уравнение энергии
.
Уравнение (3) также можно представить в
виде:
t
t
t
t
wx wy wz
x
y
z
t t t qv
a( 2 2 2 )
c
x y z
2
.
2
2
(4)

11. .

Дифференциальное
уравнение энергии
.
Левая часть уравнения (4) есть полная
производная от температуры по времени:
dt t
t
t
t
wx wy wz
d
x
y
z
t t dx t dy t dz
x d y d z d
.

12. .

Дифференциальное
уравнение энергии
.
Член
t
характеризует
изменение температуры в
отдельных точках жидкости
(локальное изменение
. температуры)

13. .

Дифференциальное
уравнение энергии
.
Член
t
t
t
wx wy wz
x
y
z
характеризует изменение температуры при
переходе от точки к точке (конвективное
.
изменение температуры)

14. Дифференциальное уравнение энергии

Обозначим:
2t
t t t
2
2
2
x y z
2
2
2

15. Дифференциальное уравнение энергии

Тогда уравнение энергии можно записать в
виде:
q
dt
2
v
a t
d
c
(5)

16. Дифференциальное уравнение энергии

При
wx wy wz 0
уравнение энергии переходит в
уравнение теплопроводности

17. Дифференциальные уравнения движения

Температурное поле в движущейся
жидкости зависит от составляющих
скорости. Для того, чтобы система
уравнений была замкнутой,
необходимо добавить уравнения,
описывающие изменение скорости во
времени и в пространстве
(дифференциальные уравнения
движения)

18. Дифференциальные уравнения движения

Дадим упрощенный вывод
дифференциального уравнения
движения для случая одномерного
течения несжимаемой жидкости. Затем для
трехмерного движения уравнение приведем
без вывода.
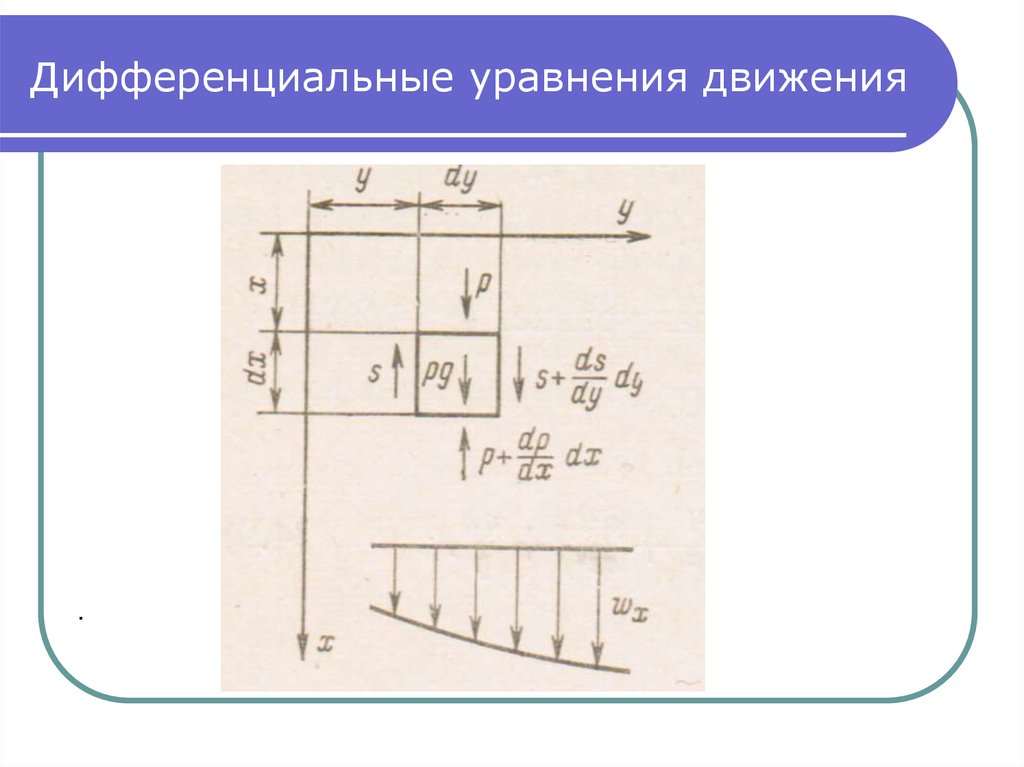
Выделим в потоке вязкой жидкости
элементарный объем с размерами ребер
dx, dy,dz. Скорость в потоке изменяется
только в направлении оси y. Закон
изменения скорости произвольный.

19. Дифференциальные уравнения движения

.

20. Дифференциальные уравнения движения

Вывод основан на втором законе Ньютона: сила равна массе,
умноженной на ускорение.
Силы, действующие на рассматриваемый элемент жидкости,
можно разделить на массовые (объемные) и
поверхностные. Массовые силы характеризуются вектором
F, м2/с, значение которого равно отношению силы,
действующей на данную частицу, к массе этой частицы.
Если учитывается только сила тяжести, то F= g, где g—
ускорение свободного падения. В дальнейшем будем
учитывать только силу тяжести. Значение поверхностных сил
равно отношению силы, действующей на элемент
поверхности, к величине площади этого элемента.
К поверхностным силам относятся силы трения и силы
давления.

21. Дифференциальные уравнения движения

Следовательно, на рассматриваемый
элемент жидкости действуют три
силы:
• Сила тяжести;
• Равнодействующая сил давления;
• Равнодействующая сил трения.

22. Дифференциальные уравнения движения

Найдем проекции этих сил на ось Ox.
Сила тяжести
df1 приложена в центре
тяжести элемента. Ее проекция на ось Ox
равна:
df1 g x dv,
Где g x - проекция ускорения свободного
падения

23. Дифференциальные уравнения движения

Сила давления на верхнюю грань:
pdydx
Сила давления на нижнюю грань:
dp
( p dx)dydz
dx

24. Дифференциальные уравнения движения

Равнодействующая сил давления равна их
алгебраической сумме:
dp
df 2 dv
dx

25. Дифференциальные уравнения движения

С учетом того, что скорость изменяется
только в направлении оси Oy, то сила
трения возникает на боковых гранях
элемента жидкости. Равнодействующая сил
трения равна:
ds
df3 dv
dy

26. Дифференциальные уравнения движения

С учетом того, что
Получим:
dwx
s
dy
ds
df3 dv
dy

27. Дифференциальные уравнения движения

Проекция на ось Ox равнодействующей всех
сил, приложенных к объему:
df df1 df 2 df3
2
dp
d wx
( gx
)dv
2
dx
dy

28. Дифференциальные уравнения движения

С другой стороны по второму закону:
dwx
df
dv
d

29. Дифференциальные уравнения движения

Приравняв правые части последних
уравнений, получим:
2
dwx
dp
d wx
gx
2
d
dx
dy

30. Дифференциальные уравнения движения

В случае трехмерного движения
несжимаемой жидкости с постоянными
физическими параметрами поле скоростей
опишется тремя уравнениями движения в
проекциях на три оси координат. Эти
уравнения называют уравнениями НавьеСтокса

31. Дифференциальные уравнения движения

Для оси Ox:
dwx
d
p
wx wx wx
gx
( 2
)
2
2
x
x
y
z
2
2
2

32. Дифференциальные уравнения движения

Для оси Oy:
dwy
d
wy wy wy
p
gy
( 2
)
2
2
y
x
y
z
2
2
2

33. Дифференциальные уравнения движения

Для оси Oz:
dwz
d
p
wz wz wz
gz
( 2
)
2
2
z
x
y
z
2
2
2

34. Дифференциальные уравнения движения

На основании понятия о полной производной
члены, стоящие в правой части уравнений
можно записать так:
Для осиOx:
dwx wx
wx
wx
wx
wx
wy
wz
d
x
y
z

35. Дифференциальные уравнения движения

Для оси Oy:
dwy
d
wy
wx
wy
x
wy
wy
y
wz
wy
z

36. Дифференциальные уравнения движения

Для оси Oz:
dwz wz
wz
wz
wz
wx
wy
wz
d
x
y
z

37. Дифференциальные уравнения движения

Уравнения Навье-Стокса в векторной форме:
dw
2
g p w
d

38. Уравнение сплошности

Ранее было установлено, что для
несжимаемых жидкостей:
wx wy wz
divw
0
x
y
z

39. Вопросы к экзамену

1.
2.
Дифференциальные уравнения
конвективного теплообмена
(уравнения энергии, сплошности).
Дифференциальные уравнения
конвективного теплообмена
(уравнения движения Навье-Стокса).