Перпендикулярность прямых и плоскостей

1. «Перпендикулярность прямых и плоскостей»

2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ

Прямая
называется перпендикулярной плоскости,
если
перпендикулярна любой прямой, лежащей в этой плоскости.
она
Теорема. (Признак перпендикулярности прямой и плоскости.) Если
прямая перпендикулярна двум пересекающимся прямым плоскости,
то она перпендикулярна и самой плоскости.
2

3. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ

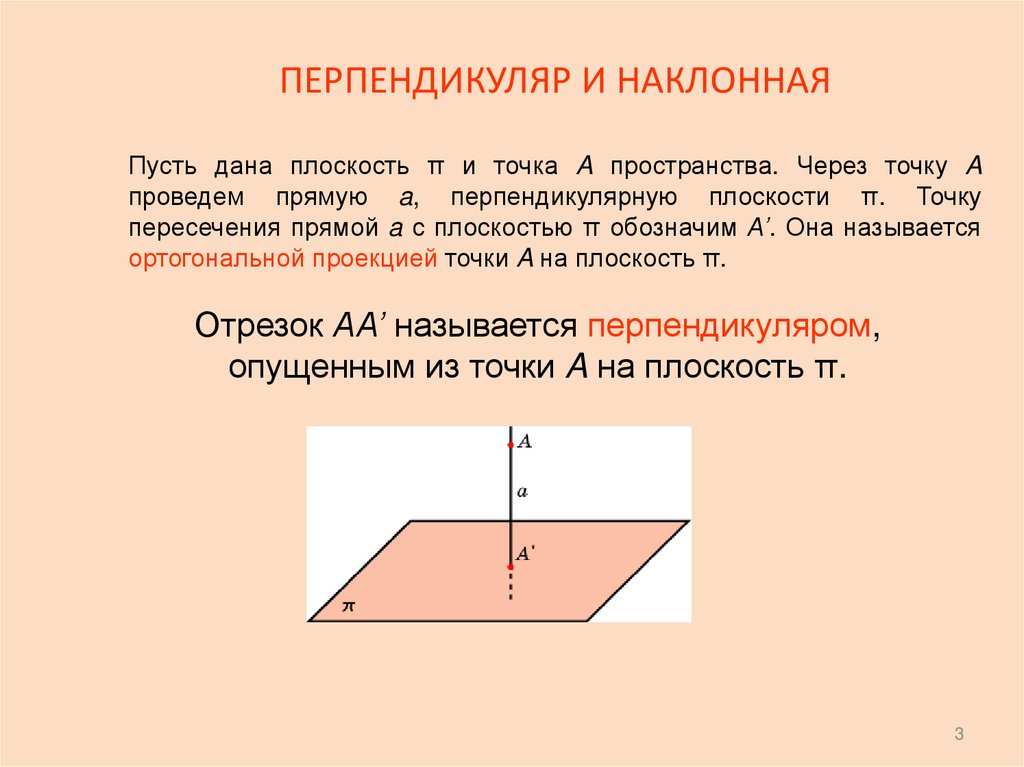
Пусть дана плоскость π и точка A пространства. Через точку A
проведем прямую a, перпендикулярную плоскости π. Точку
пересечения прямой a с плоскостью π обозначим A’. Она называется
ортогональной проекцией точки A на плоскость π.
Отрезок AA’ называется перпендикуляром,
опущенным из точки A на плоскость π.
3

4.

ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
Наклонной к плоскости называется прямая, пересекающая эту
плоскость и не перпендикулярная ей. Наклонной называют также
отрезок, соединяющий точку, не принадлежащую плоскости, с точкой
плоскости, и не являющийся перпендикуляром.
Соответствие, при котором точке A пространства сопоставляется
ортогональная проекция A’, называется ортогональным
проектированием на плоскость π.
4

5.

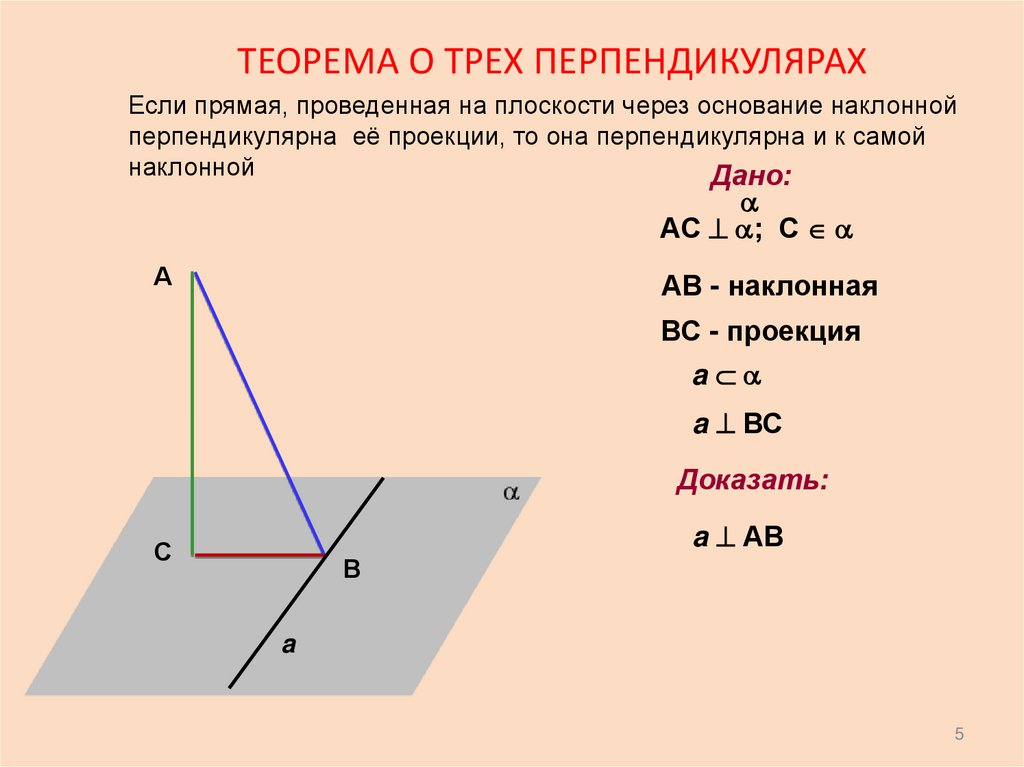
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ
Если прямая, проведенная на плоскости через основание наклонной
перпендикулярна её проекции, то она перпендикулярна и к самой
наклонной
Дано:
АС ; С
А
АВ - наклонная
ВС - проекция
a
a ВС
Доказать:
a АВ
С
В
a
5

6.

Задача 1
Установить взаимное положение прямых а и в по
готовым чертежам
Задача1. ABCD – квадрат
BE ABCD
E
a
b
B
A
C
D
6

7. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ

Две плоскости называются перпендикулярными, если угол
между ними прямой.
Теорема. (Признак перпендикулярности двух плоскостей.) Если
плоскость проходит через прямую, перпендикулярную другой
плоскости, то эти плоскости перпендикулярны.
7

8. Задача 2

В кубе A…D1 укажите плоскости, проходящие
через вершины куба, перпендикулярные
плоскости: а) ABC; б) BCD1.
8

9.

10.

Стереометрия
Планиметрия
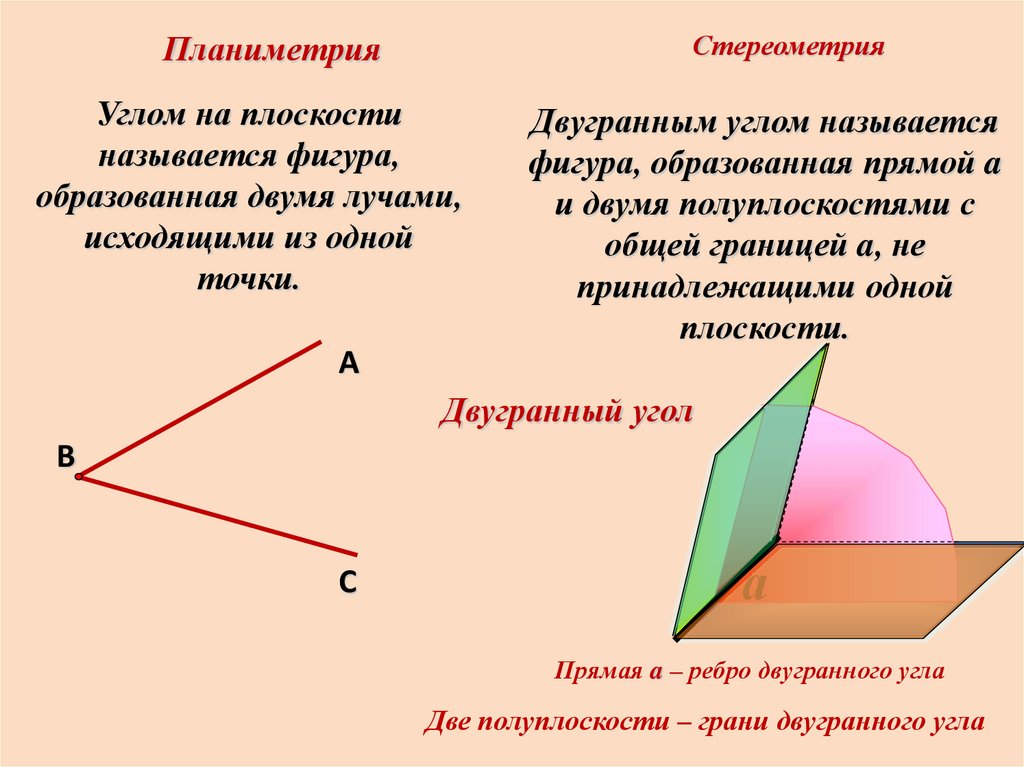
Углом на плоскости
называется фигура,
образованная двумя лучами,
исходящими из одной
точки.
Двугранным углом называется
фигура, образованная прямой a
и двумя полуплоскостями с
общей границей a, не
принадлежащими одной
плоскости.
А
Двугранный угол
В
С
а
Прямая a – ребро двугранного угла
Две полуплоскости – грани двугранного угла

11.

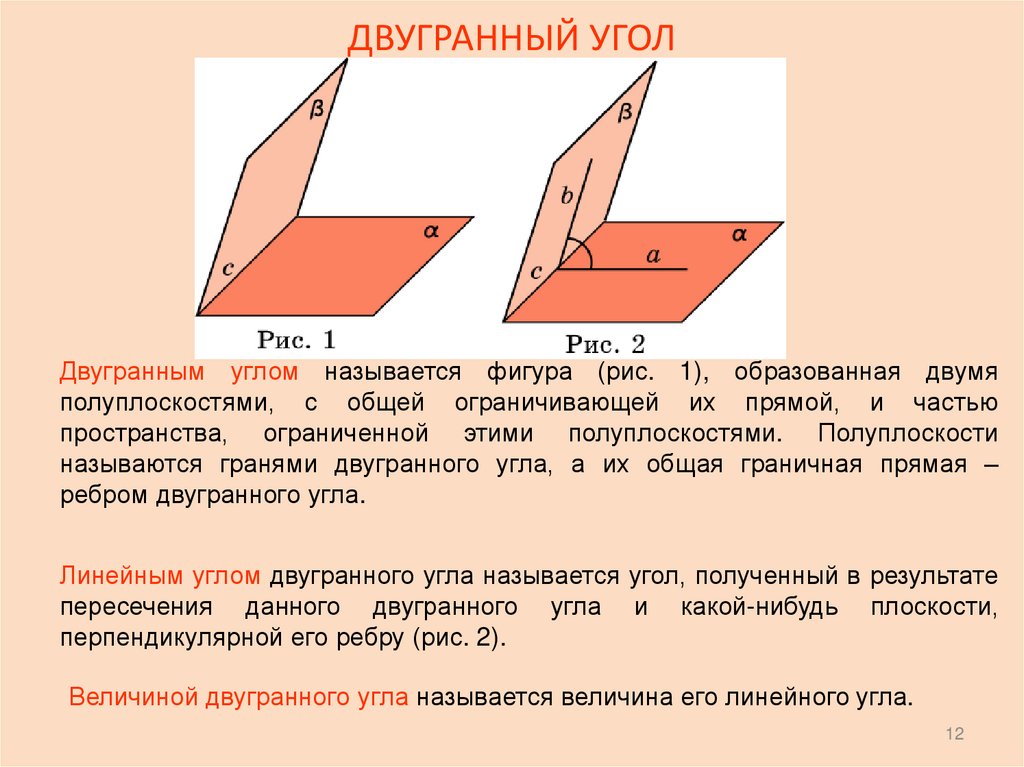
12. ДВУГРАННЫЙ УГОЛ

Двугранным углом называется фигура (рис. 1), образованная двумя
полуплоскостями, с общей ограничивающей их прямой, и частью
пространства, ограниченной этими полуплоскостями. Полуплоскости
называются гранями двугранного угла, а их общая граничная прямая –
ребром двугранного угла.
Линейным углом двугранного угла называется угол, полученный в результате
пересечения данного двугранного угла и какой-нибудь плоскости,
перпендикулярной его ребру (рис. 2).
Величиной двугранного угла называется величина его линейного угла.
12

13.

Двугранный угол АВNМ, ВN – ребро, точки А и М лежат в гранях
двугранного угла
D
Угол РDEK
S
O
А
Р
N
F
В
К
X
M
E
Угол SFX – линейный угол двугранного угла

14. Задача 3

В кубе A…D1 найдите угол между
плоскостями ABC и CDD1.
14

15. Задача 4

В кубе A…D1 найдите угол между
плоскостями ABC и CDA1.
15

16.

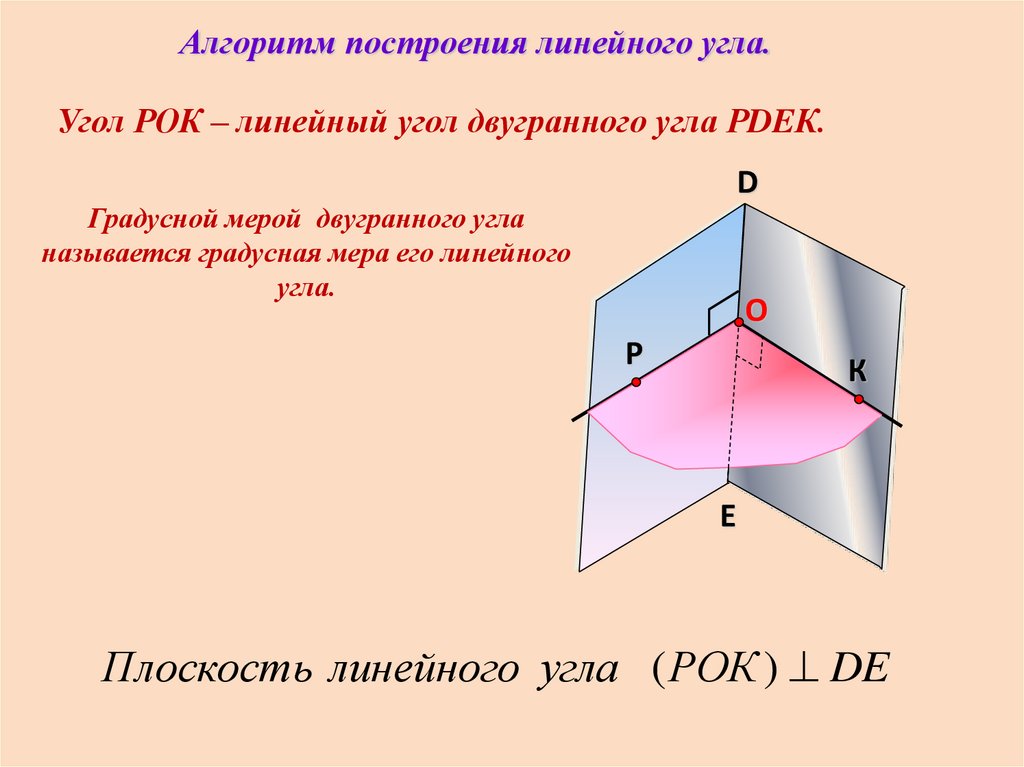
Алгоритм построения линейного угла.
Угол РОК – линейный угол двугранного угла РDEК.
D
Градусной мерой двугранного угла
называется градусная мера его линейного
угла.
O
Р
К
E
Плоскость линейного угла ( РОК ) DE

17.

Все линейные углы двугранного угла равны друг другу.
Лучи ОА и О1А1 – сонаправлены
O
Лучи ОВ и О1В1 – сонаправлены
А
В
Углы АОВ и А1О1В1 равны
как углы с сонаправленными
сторонами
O
А1
1
В1

18.

Двугранный угол может быть острым, прямым, тупым