Аналитическая геометрия. Геометрия в пространстве

1. Аналитическая геометрия

Часть 2
Геометрия в пространстве

2. Геометрический смысл уравнения с тремя переменными.

Подобно тому, как на плоскости Oxy уравнение F(x,y)=0
определяет линию, так и уравнение F(x,y,z)=0 определяет
в пространстве некоторую поверхность как
геометрическое место точек, координаты которых
удовлетворяют этому уравнению.

3. Пример

Вывод уравнения сферы радиуса R c центром в
точке Mo (xo , yo , zo ).
Сфера – это геометрическое место точек,
равноудаленных от центра. Вычислим
расстояние от произвольной точки M(x,y,z) до
центра Mo (xo , yo , zo ).
Приравняем его радиусу R и возведем в квадрат
| MM o | ( x x o )2 ( y yo )2 (z zo )2 ,
( x x o ) 2 ( y yo ) 2 (z z o ) 2 R 2
- уравнение сферы.

4. Аналитическая геометрия в пространстве.

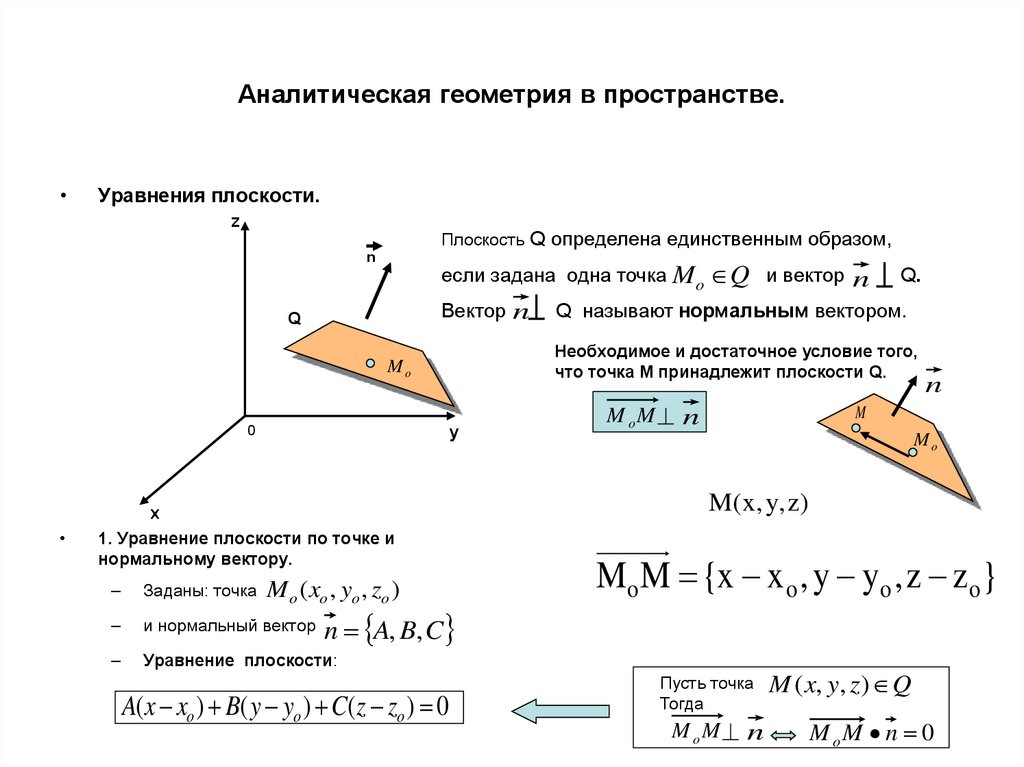
Уравнения плоскости.
z
Плоскость Q определена единственным образом,
n
если задана одна точка M o Q и вектор n
Вектор n
Q
y
M oM
n
M
n
Mo
M( x, y, z)
х
Q называют нормальным вектором.
Необходимое и достаточное условие того,
что точка М принадлежит плоскости Q.
Mo
0
Q.
1. Уравнение плоскости по точке и
нормальному вектору.
M o ( xo , yo , zo )
–
Заданы: точка
–
и нормальный вектор
–
Уравнение плоскости:
n A, B, C
A( x xo ) B( y yo ) C( z zo ) 0
Mo M {x x o , y yo , z zo }
Пусть точка
Тогда
M oM
n
M ( x, y, z) Q
M oM n 0

5. Общее уравнение плоскости

• Раскроем скобки в уравнении плоскости, проходящей через
данную точку (полученном ранее):
A( x xo ) B( y yo ) C( z zo ) 0
Ax Axo By Byo Cz Czo 0
Ax By Cz Axo Byo Czo 0
Обозначим
Получим
D Axo Byo Czo
Ax By Cz D 0
- общее уравнение плоскости

6. Пример

Составить уравнение плоскости, проходящей через точку M 0 ( 1; 2; 5 )
перпендикулярно вектору n { 4;1; 3 }
.
Решение
A( x xo ) B( y yo ) C( z zo ) 0
n A, B, C
M o ( xo , yo , zo )
4 ( x ( 1 )) 1 ( y 2 ) 3 ( z 5 ) 0
4x 4 y 2 3z 15 0
4x y 3z 13 0
Ответ:
4x y 3z 13 0

7. Аналитическая геометрия в пространстве.

2. Общее уравнение плоскости.
–
Уравнение вида
–
–
называется общим уравнением плоскости.
Коэффициенты A,B,C в уравнении определяют
координаты нормального вектора:
Ax By Cz D 0
n A, B, C
Теорема.
Всякое уравнение первой степени
с тремя переменными x,y,z вида
Ax By Cz D 0
(1)
задает плоскость в пространстве
и наоборот, всякая плоскость
в пространстве может быть задана
уравнением с тремя переменными x,y,z
вида (1).
n A, B, C
Q
Q

8. Аналитическая геометрия в пространстве.

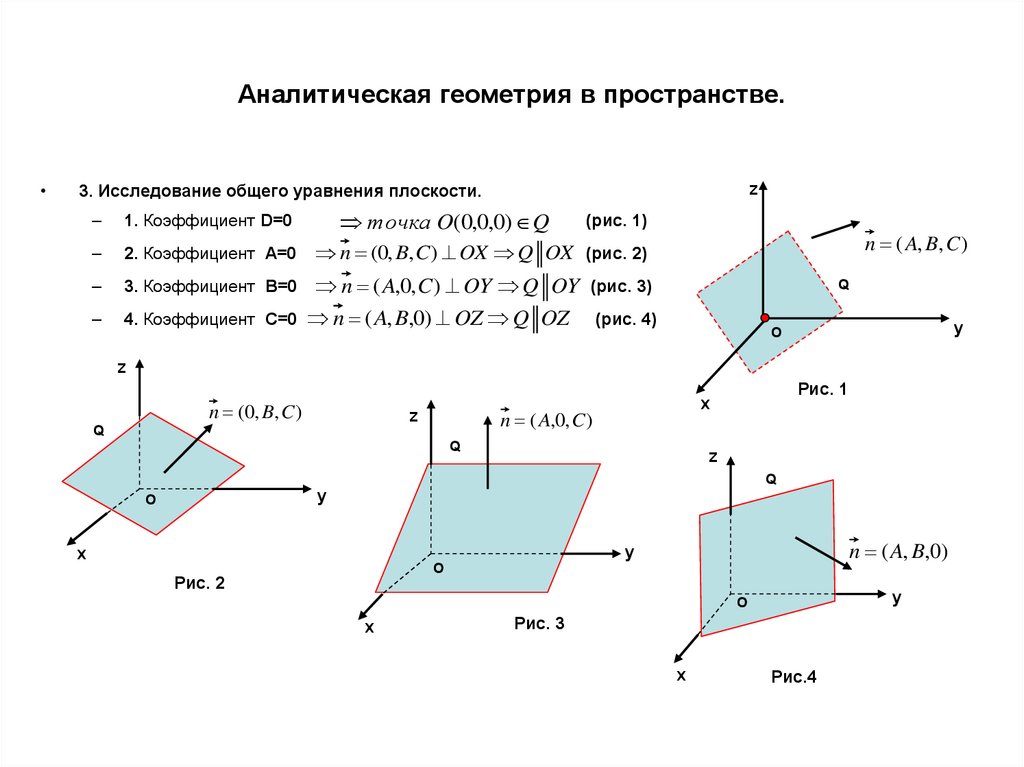
3. Исследование общего уравнения плоскости.
–
1. Коэффициент D=0
–
2. Коэффициент A=0
–
3. Коэффициент B=0
–
z
точка O(0,0,0) Q
(рис. 1)
n ( A, B, C )
n (0, B, C) OX Q OX (рис. 2)
n ( A,0, C) OY Q OY (рис. 3)
4. Коэффициент C=0 n ( A, B,0) OZ Q OZ
(рис. 4)
Q
y
O
z
n (0, B, C )
n ( A,0, C )
z
Q
Рис. 1
x
Q
z
Q
y
O
n ( A, B,0)
y
x
O
Рис. 2
y
O
x
Рис. 3
x
Рис.4

9. Аналитическая геометрия в пространстве.

–
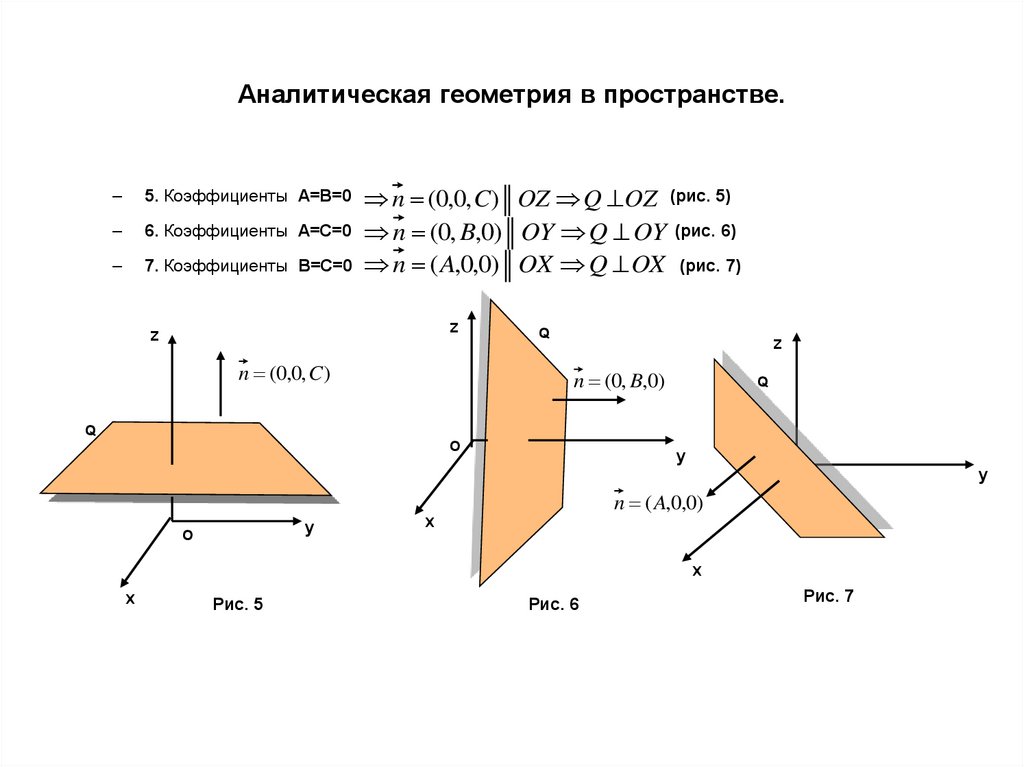
5. Коэффициенты A=B=0
–
6. Коэффициенты A=C=0
–
7. Коэффициенты B=C=0
n (0,0, C) OZ Q OZ (рис. 5)
n (0, B,0) OY Q OY (рис. 6)
n ( A,0,0) OX Q OX (рис. 7)
z
z
n (0,0, C )
Q
z
n (0, B,0)
Q
Q
O
y
O
n (A,0,0)
y
O
x
x
x
Рис. 5
Рис. 6
Рис. 7
y

10. Аналитическая геометрия в пространстве.

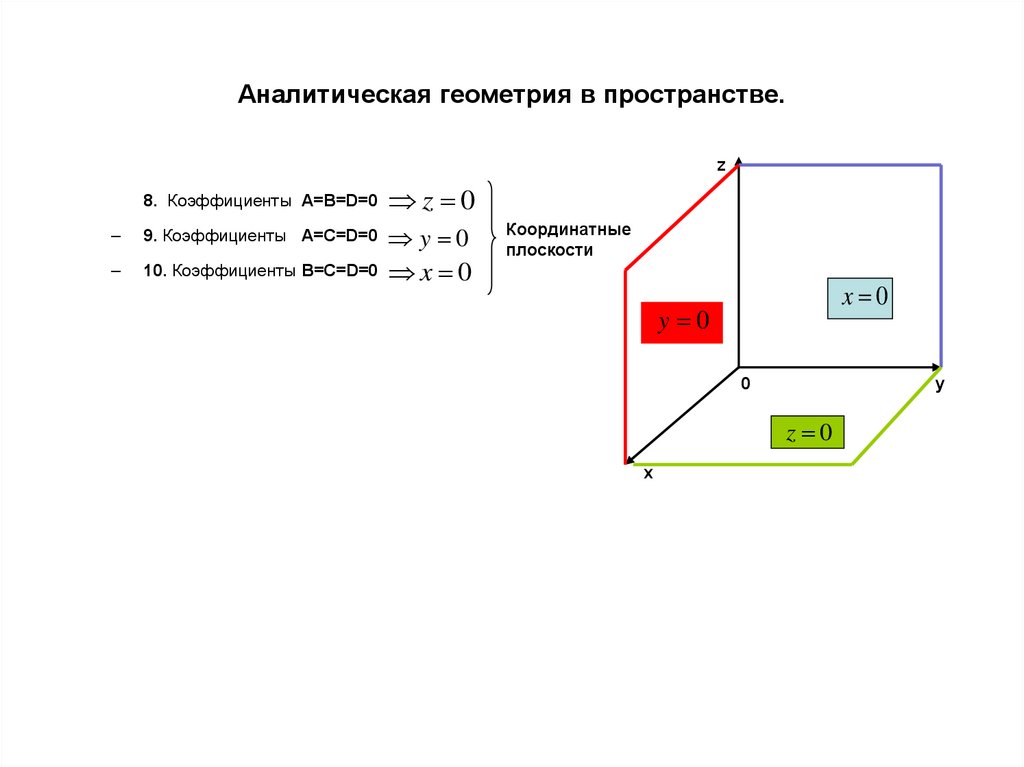
z
8. Коэффициенты A=B=D=0
z 0
–
9. Коэффициенты A=C=D=0
y 0
–
10. Коэффициенты B=C=D=0
x 0
Координатные
плоскости
x 0
y 0
0
y
z 0
x

11. Аналитическая геометрия в пространстве.

Взаимное расположение плоскостей и прямых в пространстве.
1. Условие параллельности плоскостей.
n2 A2 , B2 , C2
Q2
Q1
Q1 : A1 x B1 y C1 z D1 0
Q2 : A2 x B2 y C2 z D2 0
Q1 Q2 n1 n2
A1 B1 C1
A2 B2 C2
n1 A1 , B1 , C1
2. Условие перпендикулярности плоскостей.
Q1
Q1 Q2 n1 n2
A1 A2 B1B2 C1C2 0
n2
n1
Q2

12.

13.

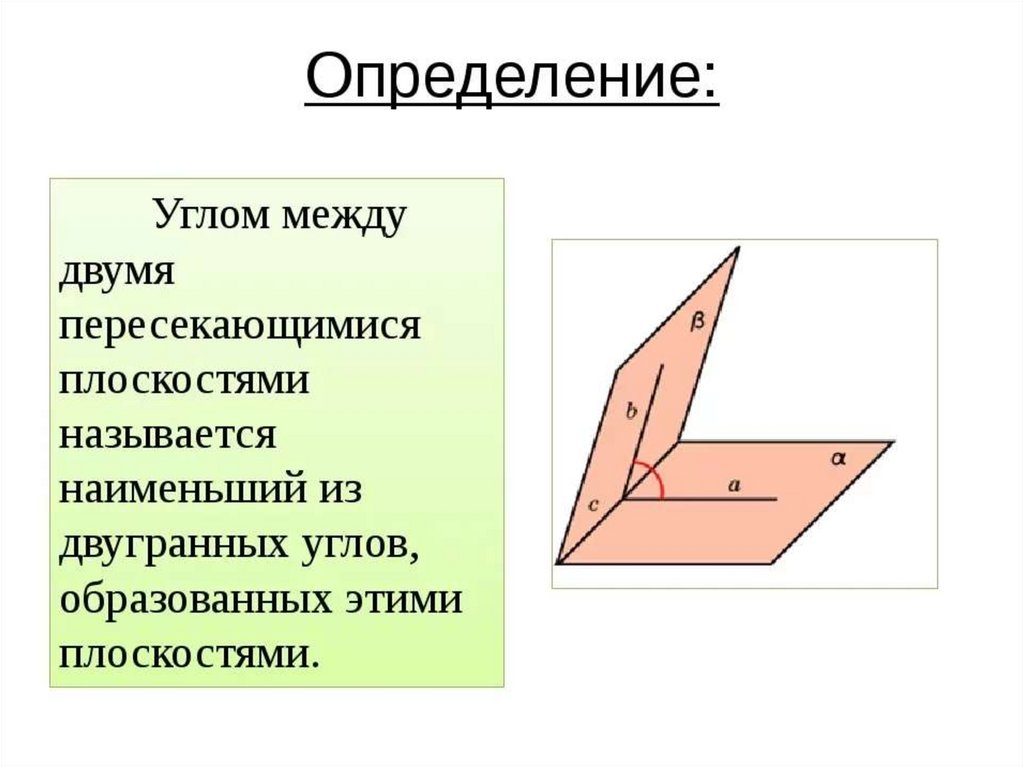
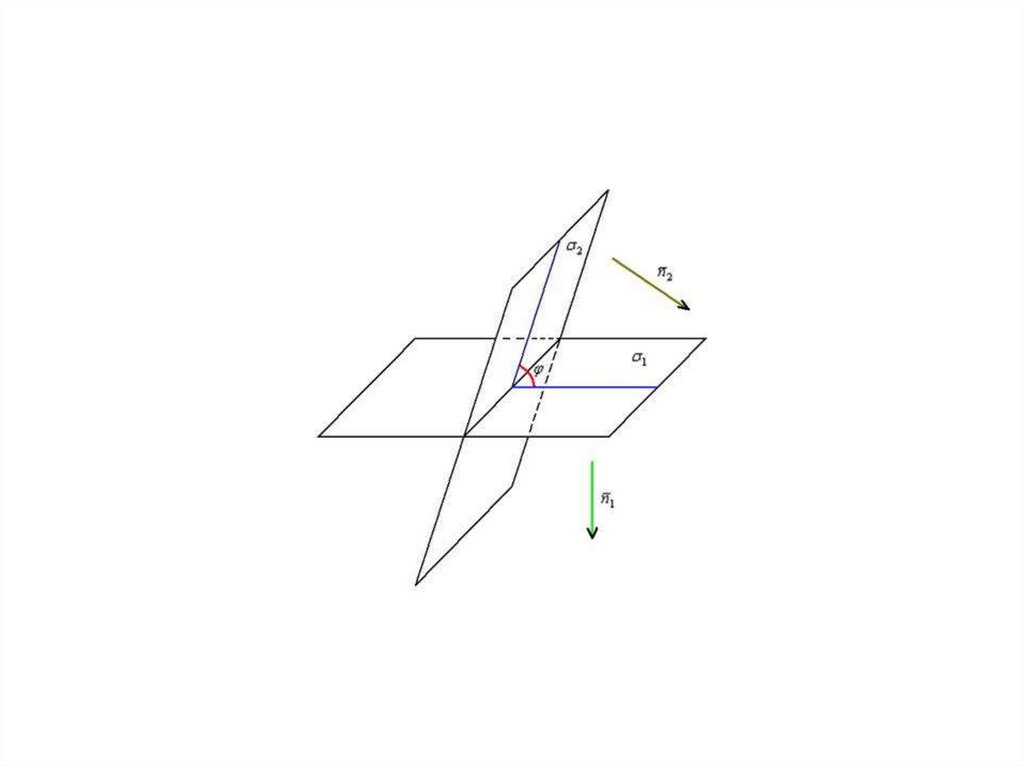
14. Угол между двумя плоскостями

A1x B1y C1z D1 0, A2 x B2 y C2z D2 0,

15. Задание линий в пространстве

Линию,в том числе и прямую, будем рассматривать как
пересечение двух поверхностей. Если эти поверхности
заданы уравнениями в виде F1(x, y, z) 0 и F2 (x, y, z) 0 ,
то линия пересечения определяется системой уравнений:
F1 ( x , y, z) 0
F2 ( x , y, z) 0

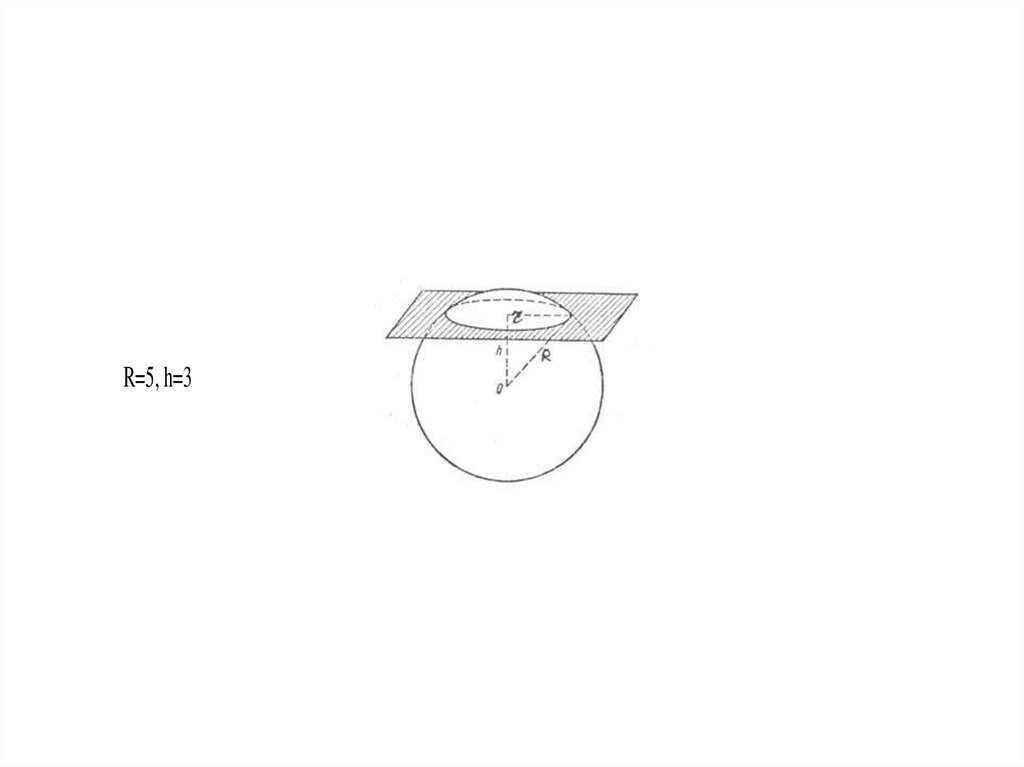
16. Пример

Рассмотрим линию, определяемую системой уравнений
x 2 y 2 z 2 25
z 3

17.

R=5, h=3

18. Аналитическая геометрия в пространстве.

Уравнения прямой в пространстве.
1. Общее уравнение прямой.
– Аксиома: линия пересечения двух
плоскостей – прямая.
l:
QQ
11
Q2
A1 x B1 y C1 z D1 0 (Q1 )
A2 x B2 y C2 z D2 0 (Q2 )
(2)
Теорема.
Система уравнений (2) определяет
прямую в пространстве тогда и только
тогда, когда коэффициенты A1 , B1 , C1
не пропорциональны коэффициентам
2
A , B2 , C2
l
Система уравнений (2) называется общим уравнением прямой.

19. Аналитическая геометрия в пространстве.

2. Канонические уравнения прямой.
s m, n, p
M ( x, y, z )
l
Mo ( xo , yo , zo )
x xo y yo z zo
m
n
p
M ( x, y, z ) l.
MoM s MoM s
Пусть точка
Тогда
3. Параметрические уравнения прямой.
x xo
x xo m
m
y yo
y yo n
n
z zo
z z o p
p
x xo m
l : y yo n
z zo p
параметр

20.

21.

22. Уравнения прямой, проходящей через две данные точки

Пусть прямая L проходит через две заданные точки:
Тогда за ее направляющий вектор можно взять
Получим уравнение прямой, проходящей через две данные точки:

23. Пример

• Даны две точки, через которые проходит прямая:
M1 (2; 3;4), M 2 (1;3;5)
• Cоставить уравнения этой прямой.
• Решение.
• Подставляя в предыдущую формулу координаты точек,
получим:
x 2
y 3
z 4
1 2
3 3
5 4
x 2
y 3
z 4
1
6
1

24. Аналитическая геометрия в пространстве.

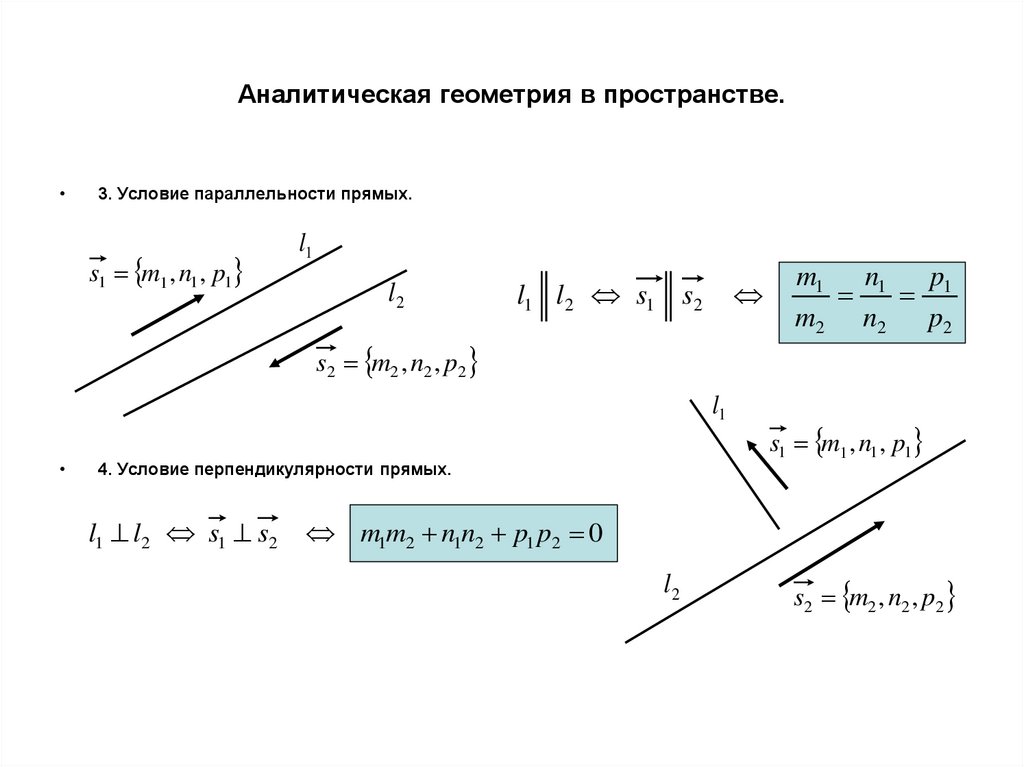
3. Условие параллельности прямых.
s1 m1 , n1 , p1
l1
l2
l1 l2 s1 s2
s2 m2 , n2 , p2
l1
4. Условие перпендикулярности прямых.
l1 l2 s1 s2
m1 n1
p
1
m2 n2 p2
s1 m1 , n1 , p1
m1m2 n1n2 p1 p2 0
l2
s2 m2 , n2 , p2

25. Угол между двумя прямыми

Угол между двумя пересекающимися прямыми – это острый угол между
ними.
Даны направляющие векторы прямых:
s1 {m1, n1.p1}, s2 {m2 , n 2 .p 2 }
s s
cos 1 2
| s1 || s2 |
В координатной форме написать самостоятельно.

26. Аналитическая геометрия в пространстве.

5. Условие параллельности прямой и плоскости.
n A, B, C
s m, n, p
l Q s n s n 0 Am Bn Cp 0
l
Q
6. Условие перпендикулярности прямой и плоскости.
s m, n, p
n A, B, C
l Q s n
Q
l
m n p
A B C

27.

Угол между прямой и плоскостью

28.

n s
cos
2
| n || s |
n s
sin
| n || s |

29. Пример

x 2
• Найти угол между прямой 4
• и плоскостью
5x 3y 4z 8 0
y 4 z 7
1
3

30.

31.

32.

33. Кривые второго порядка Окружность

34.

35. Эллипс

36.

37. Гипербола

38. гипербола

39.

40. Парабола