Похожие презентации:
Аналитическая геометрия на плоскости
1. Аналитическая геометрия
на плоскости2. Аналитическая геометрия на плоскости.
Аналитическая геометрия – это та часть математики, в которойгеометрические задачи решаются аналитическими
(алгебраическими) методами. И в этом ей помогает метод
координат. Основателем метода координат считается
французский математик и философ Рене Декарт (1596-1650г.г.).
Опубликование его “Геометрии” (приложение к философскому
трактату ”Рассуждение о методе”) в 1637 году условно
считается датой рождения аналитической геометрии.
3. РЕНЕ ДЕКАРТ (1596-1650)
4. прямоугольная (декартова) система координат
Под системой координат на плоскости или в пространстве понимаютспособ, позволяющий численно описать положение точки плоскости
или пространства. Одной из таких систем является прямоугольная
(декартова) система координат. Прямоугольная система координат
задается взаимно перпендикулярными прямыми (рис.1,2), на каждой из
которых выбрано положительное направление, и задан единичный
отрезок. Эти прямые называются осями координат, точка их
пересечения О – начало координат, ох – ось абсцисс, oy – ось ординат.
5. Важнейшим понятием аналитической геометрии на плоскости является понятие уравнения линии.
Линией, определяемой уравнением F(x,y)=0, называетсягеометрическое место точек плоскости Oxy, координаты
которых удовлетворяют этому уравнению.
Это означает, что координаты любой точки линии, при
подстановке в уравнение F(x,y) = 0 превращают его в
тождество.
А координаты любой другой точки, не принадлежащей линии,
этому уравнению не удовлетворяют.
Уравнение линии дает возможность изучение геометрических
свойств линии заменить исследованием его уравнения.
Чтобы ответить на вопрос, лежит ли точка на линии L,
достаточно знать координаты точки M и уравнение линии L.
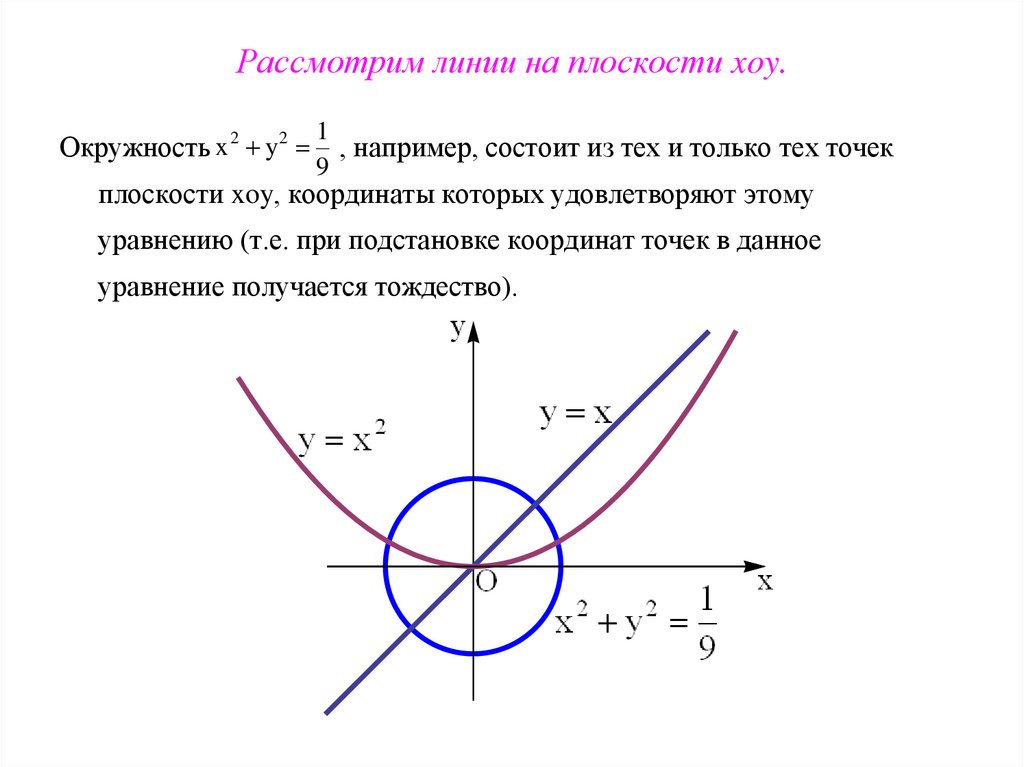
6. Рассмотрим линии на плоскости xoy.
Окружность x 2 y21
, например, состоит из тех и только тех точек
9
плоскости xoy, координаты которых удовлетворяют этому
уравнению (т.е. при подстановке координат точек в данное
уравнение получается тождество).
7. . Пример.
• Пример. Лежит ли точка K(-2,1) на линии2x+y+3=0 ?
Решение. Подставим x=-2, y=1 в уравнение
линии: 2 ( 2) 1 3 0, 0 0.
• Точка K(-2,1) лежит на данной линии.
8. Прямая на плоскости.
Простейшей из линий является прямая. Всякую прямую, не параллельнуюоси ординат, можно представить уравнением вида
y kx b
где к есть тангенс угла α, образованного прямой с положительным
направлением оси абсцисс (ox).
k tg ; M(0, b).
9. Вывод уравнения прямой с угловым коэффициентом
Прямая образует с положительнымнаправлением оси Ox угол и ордината ее
точки пересечения с осью Oy равна b.
Возьмем на прямой точку M( x, y,) тогда
OA x , AM y , MN y b , MN x tg .
Так как k tg , получим y b kx или
y kx b.
10.
Величину к называют угловым коэффициентом.Величину b – начальной ординатой.
Если прямая параллельна оси ox, то уравнение
прямой примет вид:
y=b
11.
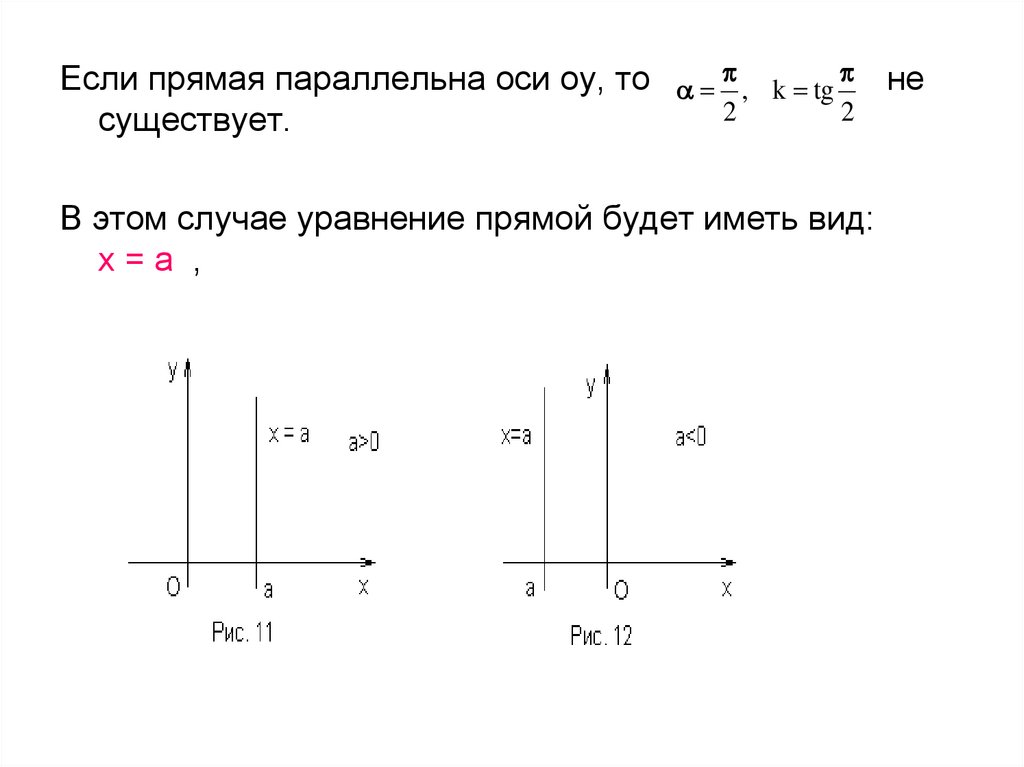
Если прямая параллельна оси oy, то , k tg не2
2
существует.
В этом случае уравнение прямой будет иметь вид:
x=a ,
где а – абсцисса точки, через которую проходит
данная прямая ( точки пересечения прямой с осью
ox).
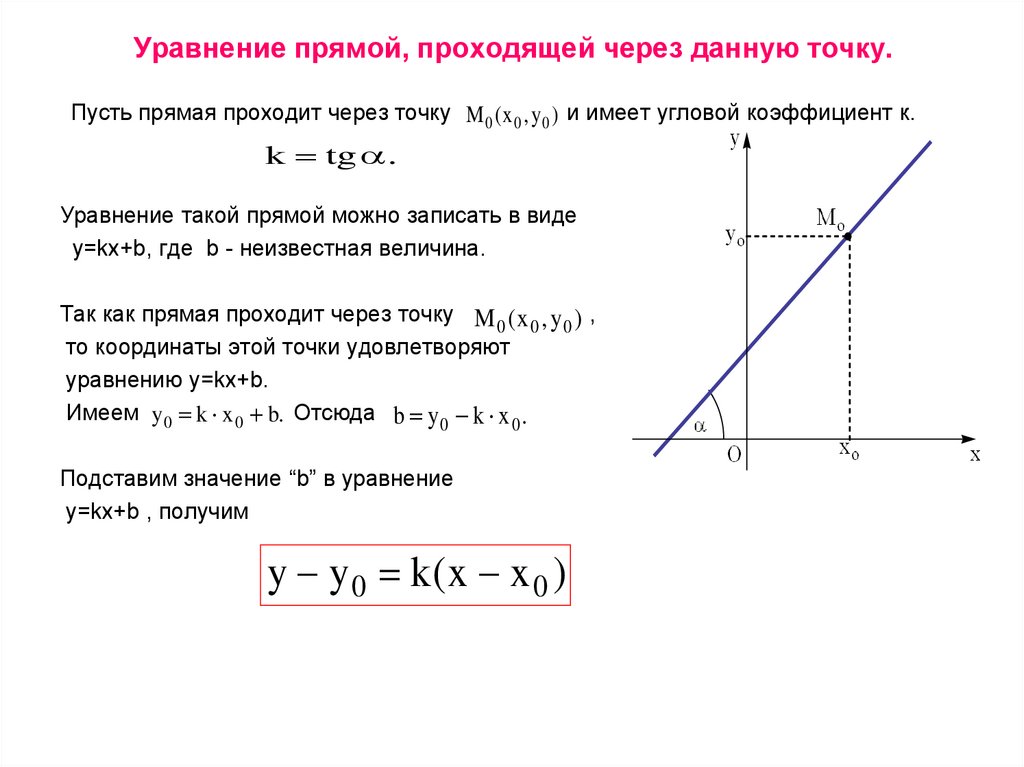
12. Уравнение прямой, проходящей через данную точку.
Пусть прямая проходит через точку M 0 ( x 0 , y 0 ) и имеет угловой коэффициент к.k tg .
Уравнение такой прямой можно записать в виде
y=kx+b, где b - неизвестная величина.
Так как прямая проходит через точку M ( x , y ) ,
0 0 0
то координаты этой точки удовлетворяют
уравнению y=kx+b.
Имеем y 0 k x 0 b. Отсюда b y 0 k x 0 .
Подставим значение “b” в уравнение
y=kx+b , получим
y y0 k(x x 0 )
13. Пример
Составить уравнение прямой, проходящей через точку Mo (1; 2)и образующей угол 135o с положительным направлением оси ox.
Решение
o
Найдем угловой коэффициент прямой: k tg135 1 .
Используем уравнение прямой, проходящей через данную точку:
y y0 k(x x 0 )
Подставляем числовое значение углового коэффициента и координаты
точки Mo .
y ( 2) 1( x 1), y x 1,
x y 1 0.
14.
Уравнение прямой по точке и направляющему вектору.Пусть прямая проходит через точку M 0 (x 0 ; y 0 ).
Направляющим вектором данной прямой
называется вектор, параллельный этой прямой.
Пусть дан вектор s {m; n} , параллельный
прямой.
Возьмем на прямой произвольную точку M(x,y) и
рассмотрим вектор MoM {x x o , y yo} .
Векторы s {m; n} и Mo M
коллинеарны,
следовательно, их соответствующие
координаты пропорциональны:
x x 0 y y0
m
n
Полученное уравнение является уравнением прямой по точке и
направляющему вектору.
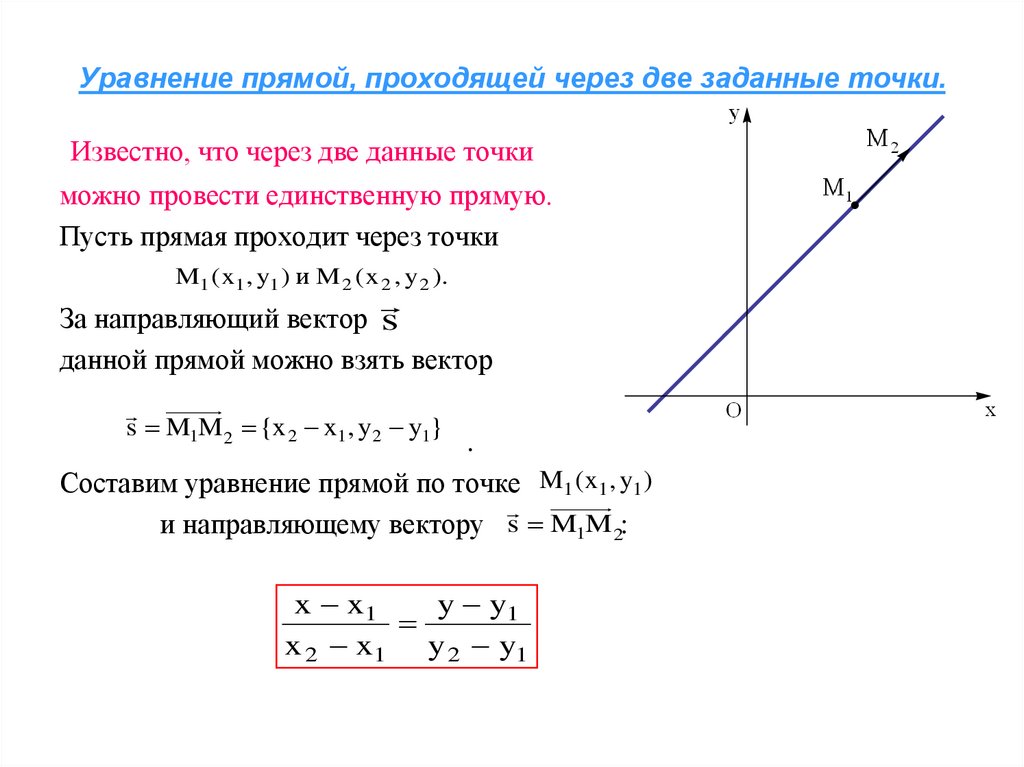
15. Уравнение прямой, проходящей через две заданные точки.
Известно, что через две данные точкиможно провести единственную прямую.
Пусть прямая проходит через точки
M1 ( x1 , y1 ) и M 2 ( x 2 , y 2 ).
За направляющий вектор s
данной прямой можно взять вектор
s M1M 2 {x 2 x1, y2 y1}
.
Составим уравнение прямой по точке M1 ( x1 , y1 )
и направляющему вектору s M1M 2:
x x1
y y1
x 2 x1 y 2 y1
16.
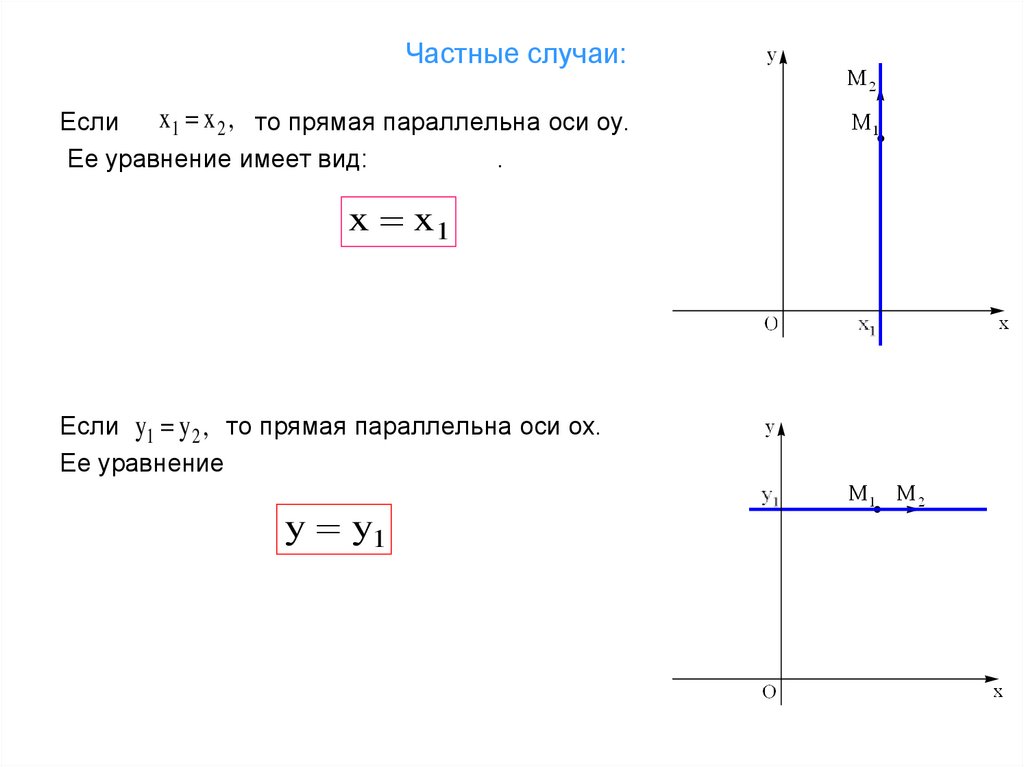
17. Частные случаи:
x1 x 2 , то прямая параллельна оси oy.Если
Ее уравнение имеет вид:
.
x x1
Если y1 y 2 , то прямая параллельна оси ox.
Ее уравнение
y y1
18. Общее уравнение прямой.
Ax + By + C = 0это уравнение называется общим уравнением прямой.
C
1). Если А = 0, то уравнение примет вид By + C = 0 ; y = - B .
Прямая параллельна оси ox.
C
2). Если В = 0, то уравнение примет вид: Ax + C = 0, x = - .
A
Прямая параллельна оси oy.
3). Если С = 0, то уравнение примет вид: Ax + By = 0. y = -
A
x.
B
Прямая проходит через начало координат и имеет угловой коэффициент k = - A .
B
19. Задача для самостоятельного решения *
• Даны векторы,совпадающие со
сторонами треугольника ABC. Найти
разложение по базису b ,c вектора,
приложенного к вершине B и
совпадающего с высотой треугольника BD.
Ответ: BD
b c
c b
c2
20.
Из общего уравнения прямой, если B 0, можно найти угловойкоэффициент к.
Для этого выразим y из этого уравнения : Ax + By + C = 0.
By = - Ax – C ;
y
A
C
x .
B
B
k
A
B
21. Пример
Найти угловой коэффициент k прямой 3x 5y 11 0 .Сравнивая с формулой Ax + By + C = 0, видим, что
A = 3, B = 5, значит по формуле k A получим:
B
k
3
.
5
22.
23. Взаимное расположение прямых на плоскости.
Угол между двумя пересекающимися прямыми.Углом между двумя пересекающимися прямыми
называется острый угол между ними. На рисунке это
угол .
Уравнение первой прямой L1 : y k1x b1 .
Уравнение второй прямой
tg 1 k1,
L2 : y k 2 x b2 , значит
tg 2 k 2,
2 1,
tg tg( 2 1 )
tg 2 tg 1 k 2 k1
;
1 tg 1tg 2 1 k1k 2
Формула для нахождения острого угла между прямыми имеет вид:
tg
k 2 - k1
1 k 1k 2
24. Условие параллельности двух прямых.
Пусть даны две прямыеL1 : y k1x b1 и L 2 : y k 2 x b 2 .
Так как прямые параллельны, то они имеют одинаковый угол наклона с осью ox
и, следовательно, одинаковые угловые коэффициенты:
k1 k 2 .
25.
26. Условие перпендикулярности двух прямых.
Если две прямые L1 : y k1x b1 и L 2 : y k 2 x b 2 взаимно перпендикулярны, то уголмежду ними 90 o.
формуле tg
k 2 - k1
1 k 1k 2
Так как tg 90 o не существует, то это означает, что в
знаменатель равен 0: 1 k1k 2 0.
или
k2
Отсюда k1k 2 1
1
k1
Это и есть условие перпендикулярности двух
прямых.






















 Математика
Математика








