Похожие презентации:
Аналитическая геометрия. Прямая на плоскости
1. Аналитическая геометрия
2. Прямая на плоскости
3.
Определение. Уравнением линии наплоскости Oxy называется
уравнение, которому удовлетворяют
координаты x и y любой точки
данной линии и не удовлетворяют
координаты любой точки, не лежащей
на этой линии.
4.
Теорема. Всякое уравнение первойстепени Ax By C 0,
где А и В
не обращаются в нуль
одновременно, представляет собой
уравнение некоторой прямой линии на
плоскости Oxy.
5. Уравнение прямой, проходящей через точку перпендикулярно вектору
6.
Введем следующие понятия. Вектор,перпендикулярный прямой l , будем
называть нормалью прямой и
обозначать n . Итак, n l .
Вектор, параллельный прямой,
будем называть направляющим
вектором этой прямой. Обозначим его
a m, p .
7.
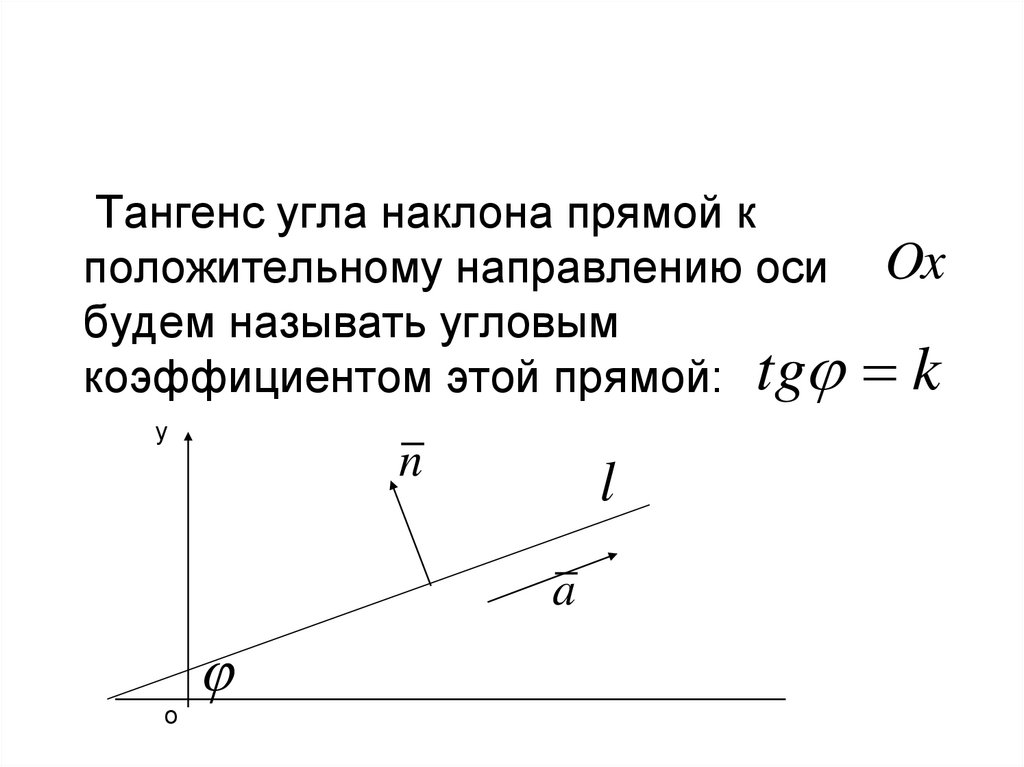
Тангенс угла наклона прямой кположительному направлению оси Ox
будем называть угловым
коэффициентом этой прямой: tg k
у
n
l
a
о
х
8.
Пусть точка M 0 x0 , y0лежит на
прямой. Точка M x, y -произвольная
точка прямой.
n A, B ;
M ( x, y )
M 0 x0 , y0
.
M 0M n
9.
Тогда скалярное произведениеn M 0 M A( x x0 ) B( y y0 ) 0.
10.
Получили уравнение прямой,проходящей через заданную точку,
перпендикулярно данному вектору:
A( x x 0) B( y y 0) 0
11. Общее уравнение прямой
Из предыдущего уравнения легкополучаем общее уравнение прямой
Ax By C 0
12. Каноническое уравнение прямой
13.
Пусть M 0 x0 ; y0 la m; p
и
M x; y
M 0 x0 ; y 0
a || l
l
14.
Тогда из условия коллинеарностивекторов M 0 M ( x x0 , y y0 )
и a m, p ; получаем каноническое,
т. е. простейшее уравнение прямой:
x x0 y y 0
m
p
15. Пример
Написать уравнения прямых,проходящих через точку M 0 2, 1
параллельно и перпендикулярно
вектору AB 3, 1 .
x
2
y
1
Первое уравнение
3
1
второе
3( x 2) ( y 1) 0 .
и
16. Уравнение прямой, проходящей через две точки
17.
ПустьM 1 x1 ; y1 l
M 2 x2 ; y2 l
M ( x, y )
M 2 x2 , y2 ;
M1 x1, y1
M 1 M || M 1 M 2
18.
Координаты этих векторовпропорциональны:
y y
x x
x x y y
1
2
1
1
2
Получили уравнение прямой,
проходящей через две точки.
1
19. Параметрические уравнения прямой
Приравняем обе части соотношенияx x0 y y0
l
m
к t. Получим параметрические уравнения
прямой
x mt x0
y pt y0
20. Уравнение прямой с угловым коэффициентом
Преобразуем уравнениек виду
x x1
y y1
x2 x1 y2 y1
y2 y1
y y1
( x x1 )
x2 x1
y2 y1
y
( x x1 ) y1
x2 x1
21.
ОбозначивM 2 x2 , y2 ;
y2 y1
k , y1 kx1 b ,
x2 x1
где k tg ,
получим
y kx b
M1 x1, y1
22. Уравнение прямой ,проходящей через точку
Пусть точка M 0 x0 , y0 лежит напрямой y k x b . Тогда y0 kx0 b.
Вычтем из первого второе соотношение .
Получим
y y0 k x x0
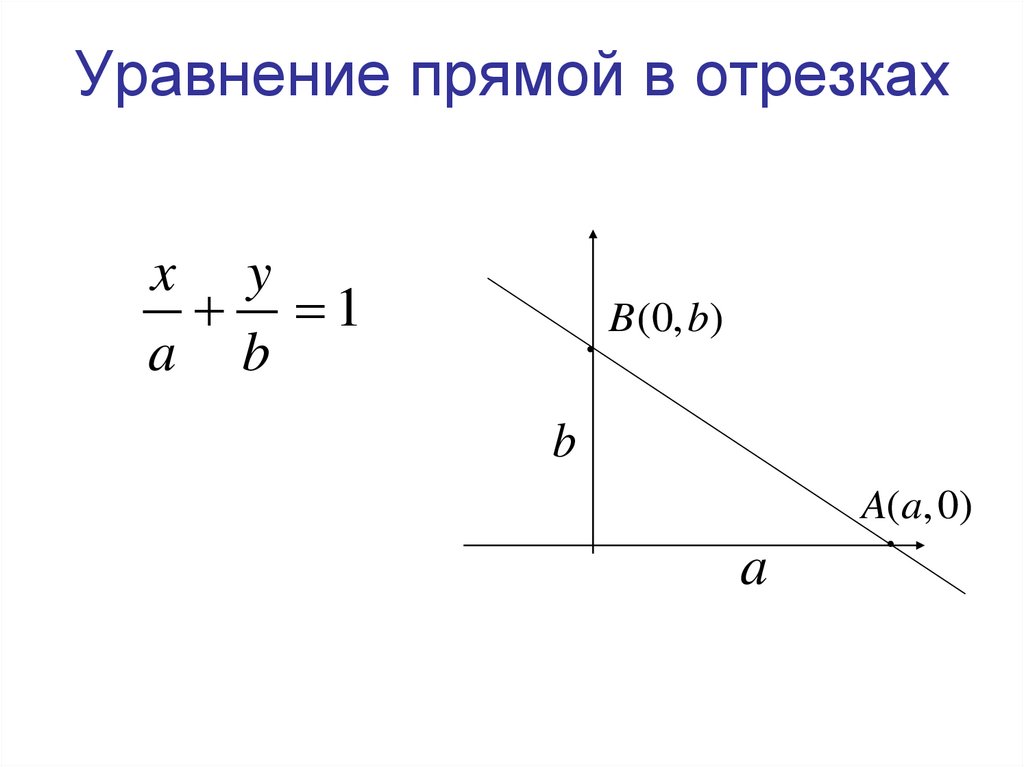
23. Уравнение прямой в отрезках
x y1
a b
B (0, b)
b
A(a, 0)
a
24. Взаимное расположение прямых
25. Угол между двумя прямыми
Пусть две прямые заданы общимиуравнениями
l1 : A1 x B1 y C1 0, n1 A1 ; B1
l2 : A2 x B2 y C2 0, n2 A2 ; B2
26.
Тогда угол между этими прямымиравен углу между их нормалями , т. е.
cos
A1 A2 B1 B2
2
A1
2
B1
2
A2
2
B2
.
27.
Пусть даны прямыеl1 : y k1 x b1
l2 : y k 2 x b2
2 1
1
2
28.
Тогдаtg 2 tg 1
k2 k1
tg 2 1
1 tg 1 tg 2 1 k1 k2
k
k
tg
1 k k
2
1
1
2
29. Условия параллельности
Прямые параллельны тогда и толькотогда, когда выполняется одно из двух
условий ( в зависимости от вида
уравнений прямых).
l1 || l2 k1 k 2
A1 B1
A2 B2
30. Условие перпендикулярности
l1 l2 k1 k 2 1A1 A2 B1 B2 0
31. Расстояние от точки до прямой
Расстояние от точки M 0 x0 , y0 допрямой Ax By C 0 находят по
формуле
.
d
Ax0 By0 C
A B
2
2
32. Пример
Найти уравнение прямой, проходящейчерез точки A1 5, 1
и A2 2,5 .







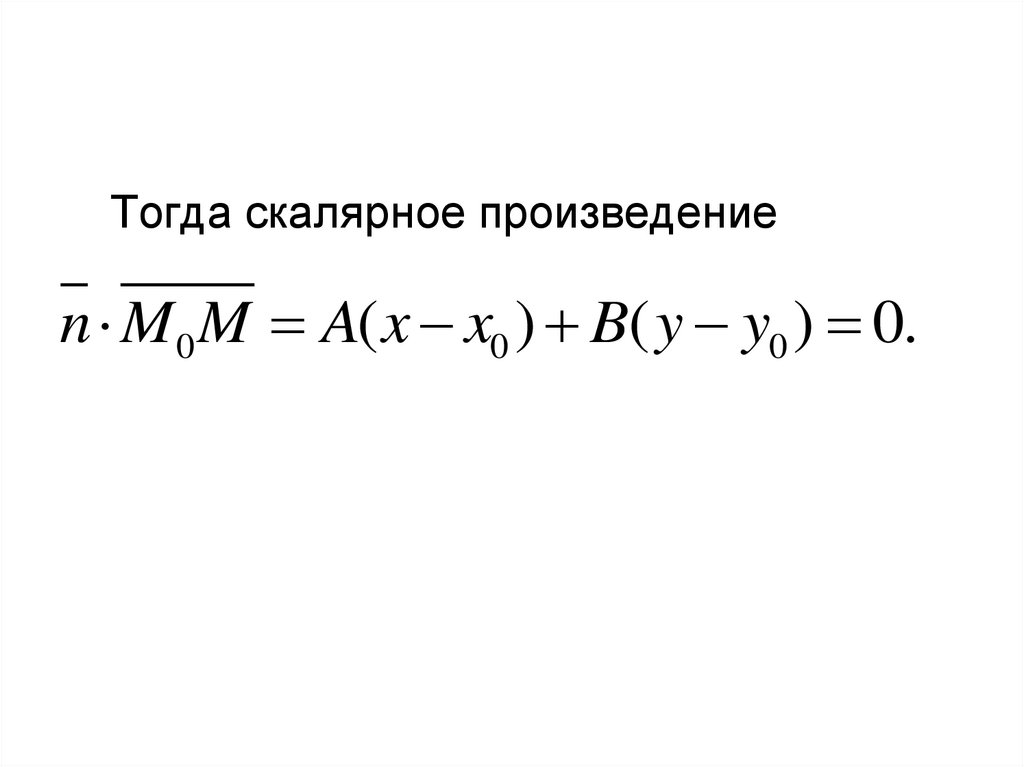



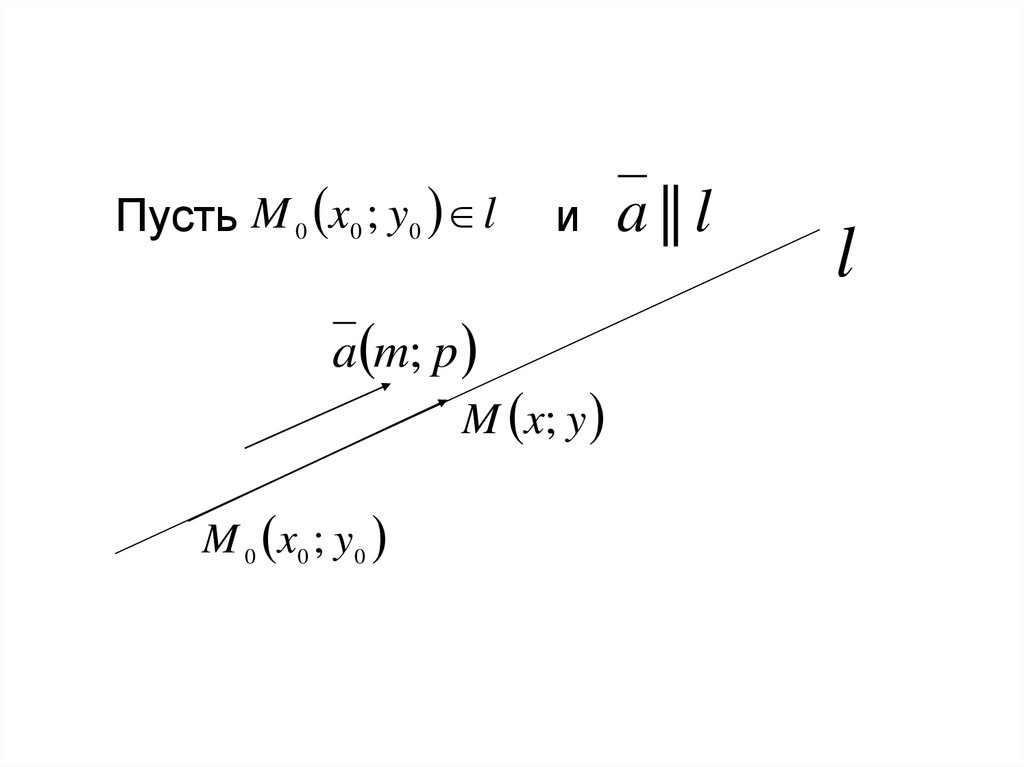


















 Математика
Математика








