Похожие презентации:
Основные теоремы и методы анализа резистивных цепей
1. Основные теоремы и методы анализа резистивных цепей.
2.
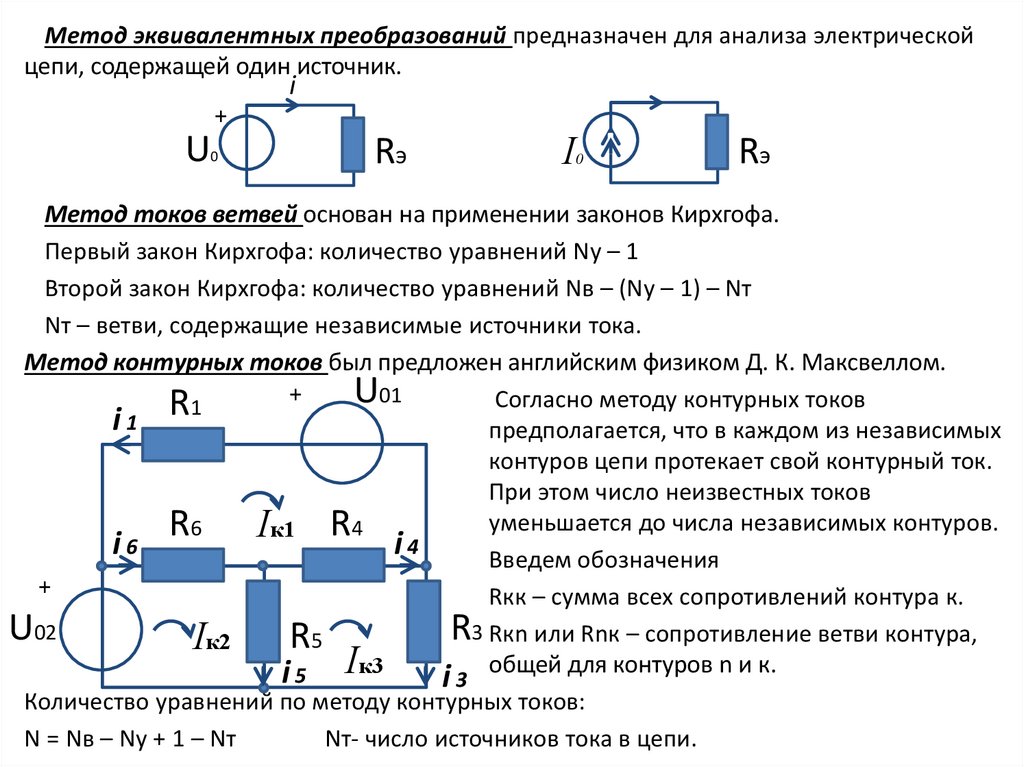
Метод эквивалентных преобразований предназначен для анализа электрическойцепи, содержащей один источник.
i
+
U
0
Rэ
І
0
Rэ
Метод токов ветвей основан на применении законов Кирхгофа.
Первый закон Кирхгофа: количество уравнений Nу – 1
Второй закон Кирхгофа: количество уравнений Nв – (Nу – 1) – Nт
Nт – ветви, содержащие независимые источники тока.
Метод контурных токов был предложен английским физиком Д. К. Mаксвеллом.
+
U01
Согласно методу контурных токов
R
1
i1
предполагается, что в каждом из независимых
контуров цепи протекает свой контурный ток.
При этом число неизвестных токов
уменьшается до числа независимых контуров.
R
6
R
4
І
к1
i6
i4
Введем обозначения
+
Rкк – сумма всех сопротивлений контура к.
U02
R3 Rкn или Rnк – сопротивление ветви контура,
Ік2 R5
i 5 Ік3
i 3 общей для контуров n и к.
Количество уравнений по методу контурных токов:
N = Nв – Nу + 1 – Nт
Nт- число источников тока в цепи.
3.
Применяя методы теории определителей в системе контурных уравнений,находим по формуле Крамера следующее решение для первого контурного тока.
Введение контурных токов в расчет позволяет исключить из системы уравнений
Кирхгофа все уравнения, составленные по первому закону, и сохранить
уравнения только для контуров.
4.
Метод узловых напряжений (МУН) позволяет сохранить только те уравненияКирхгофа, которые составлены для узлов, и исключить все уравнения для
контуров.
МУН заключается в том, что на основании первого закона Кирхгофа
определяются напряжения в узлах электрической цепи относительно некоторого
базисного узла. Потенциал базисного узла ϕ0 считается равным 0 (ϕ0 =0). Эти
искомые напряжения называются узловыми напряжениями.
Система уравнений, составленных по методу узловых напряжений, имеет вид:
Gкк – собственная проводимость к-ого узла; определяется как сумма
проводимостей всех ветвей, подключенных к к-ому узлу (Gкк>0).
Giк – взаимная проводимость; проводимость ветвей, соединяющих «i» и «к»
узлы, не пересекая другие узлы (Giк<0).
– алгебраическая сумма токов, которые протекали бы в ветвях,
присоединенных к n-ому узлу, если каждую из них замкнуть накоротко, к
узлу «плюс» от узла «минус».
5.
R1i1
U01
+
R4
1
2
i4
i 01
R2
i2
3
R3
i 02
i3
6.
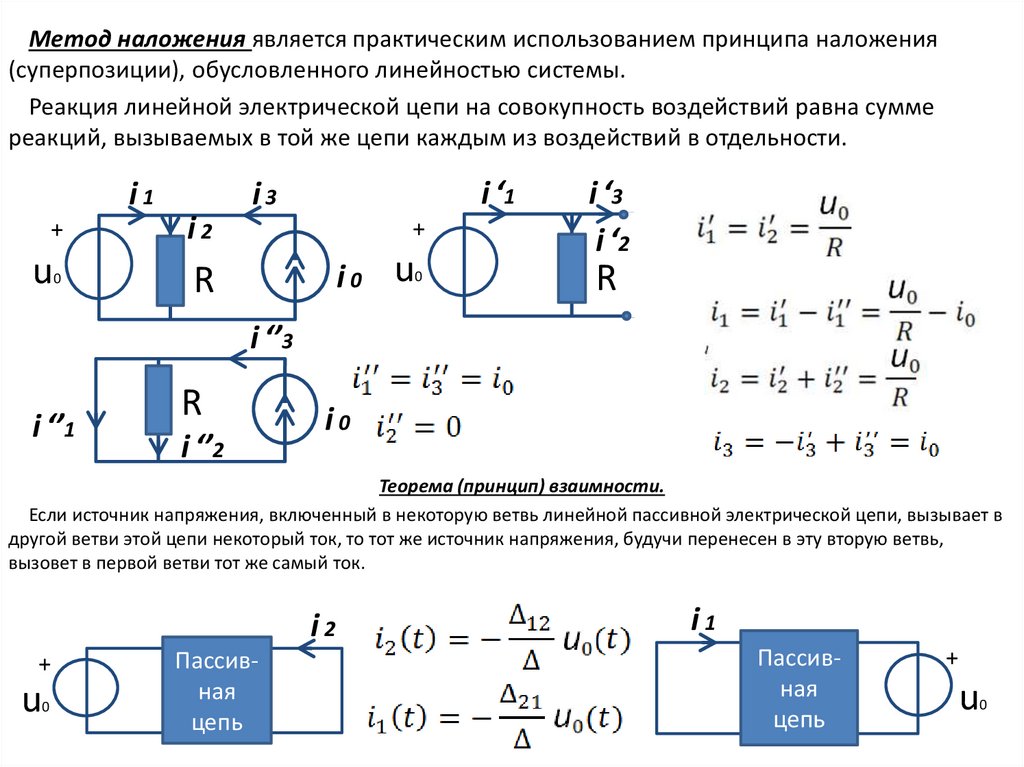
Метод наложения является практическим использованием принципа наложения(суперпозиции), обусловленного линейностью системы.
Реакция линейной электрической цепи на совокупность воздействий равна сумме
реакций, вызываемых в той же цепи каждым из воздействий в отдельности.
i1
+
u
0
i ‘1
i3
i2
+
R
i 0 u0
i ‘3
i ‘2
R
i ‘’3
i ‘’1
R
i ‘’2
i0
Теорема (принцип) взаимности.
Если источник напряжения, включенный в некоторую ветвь линейной пассивной электрической цепи, вызывает в
другой ветви этой цепи некоторый ток, то тот же источник напряжения, будучи перенесен в эту вторую ветвь,
вызовет в первой ветви тот же самый ток.
i2
+
u
0
Пассивная
цепь
i1
Пассивная
цепь
+
u
0
7.
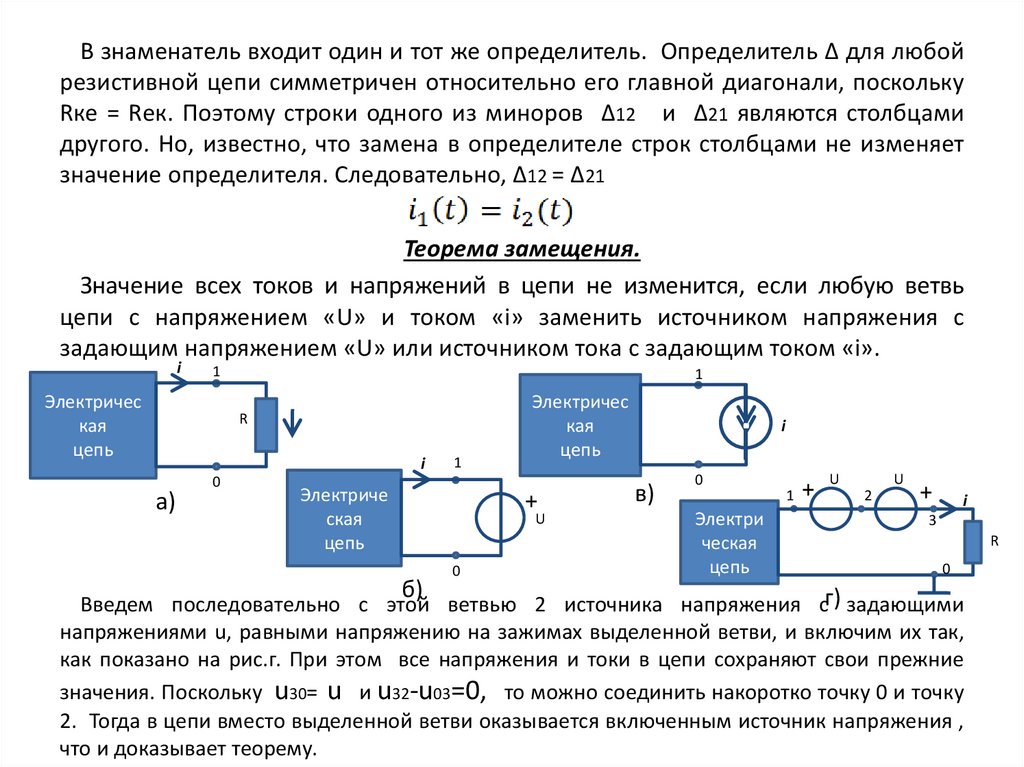
В знаменатель входит один и тот же определитель. Определитель Δ для любойрезистивной цепи симметричен относительно его главной диагонали, поскольку
Rке = Rек. Поэтому строки одного из миноров Δ12 и Δ21 являются столбцами
другого. Но, известно, что замена в определителе строк столбцами не изменяет
значение определителя. Следовательно, Δ12 = Δ21
Теорема замещения.
Значение всех токов и напряжений в цепи не изменится, если любую ветвь
цепи с напряжением «U» и током «i» заменить источником напряжения с
задающим напряжением «U» или источником тока с задающим током «i».
i
1
Электричес
кая
цепь
1
R
i
а)
0
1
Электриче
ская
цепь
Электричес
кая
цепь
+
U
б)
0
i
в)
0
Электри
ческая
цепь
1
+
U
U
2
+
i
3
R
0
Введем последовательно с этой ветвью 2 источника напряжения сг) задающими
напряжениями u, равными напряжению на зажимах выделенной ветви, и включим их так,
как показано на рис.г. При этом все напряжения и токи в цепи сохраняют свои прежние
значения. Поскольку u30= u и u32-u03=0, то можно соединить накоротко точку 0 и точку
2. Тогда в цепи вместо выделенной ветви оказывается включенным источник напряжения ,
что и доказывает теорему.
8.
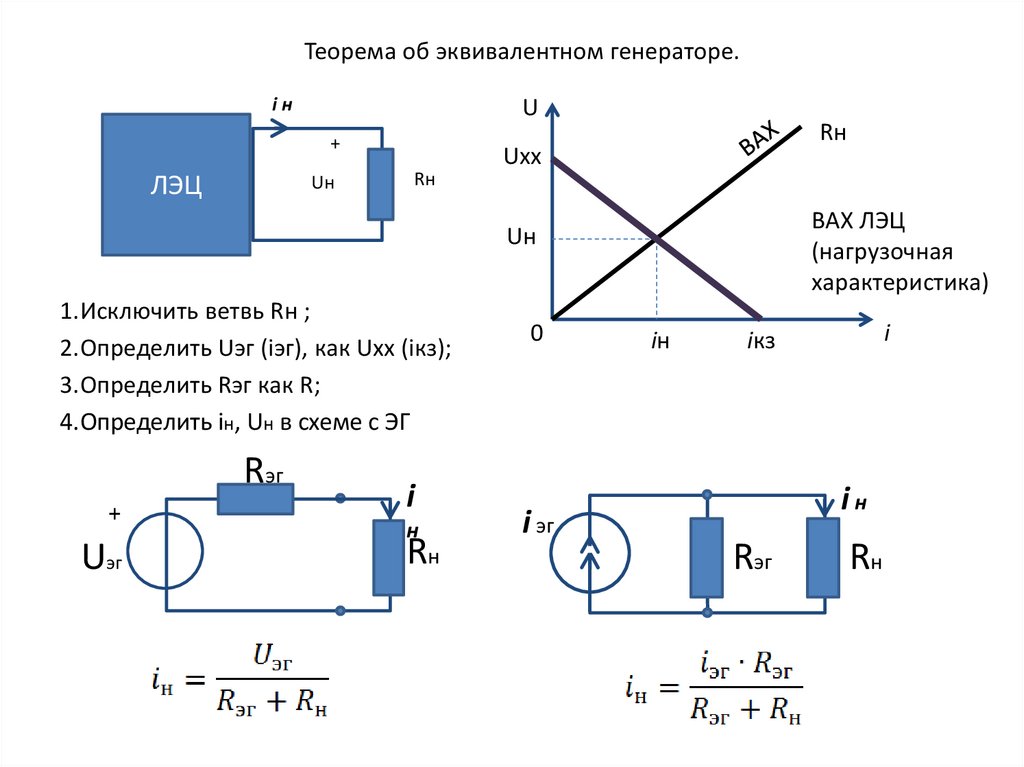
Теорема об эквивалентном генераторе.iн
U
+
ЛЭЦ
Uн
Rн
Rн
Uхх
ВАХ ЛЭЦ
(нагрузочная
характеристика)
Uн
1.Исключить ветвь Rн ;
2.Определить Uэг (iэг), как Uхх (iкз);
3.Определить Rэг как R;
4.Определить iн, Uн в схеме с ЭГ
Rэг
+
Uэг
i
н
Rн
0
i эг
iн
i
iкз
iн
Rэг
Rн
9.
Теорема Телледжена. Баланс мощности.Сумма произведений напряжений Uк и токов iк всех ветвей в электрической
цепи равна нулю.
Терема Телледжена следует из законов Кирхгофа, справедлива для любых
электрических цепей: линейных и нелинейных, активных и пассивных; цепей,
параметры которых изменяются во времени (параметрических цепей).
Можно сформулировать баланс мощности: «Алгебраическая сумма мощностей,
отдаваемых независимыми источниками, равняется алгебраической сумме
мощностей, потребляемых остальными ветвями электрической цепи.
Pист = Pпотр





 Физика
Физика








