Кинематика материальной точки

1.

Механика.
Кинематика материальной точки
Лектор: к.ф.-м.н., доц. Козубай Искендер

2.

Курс Общей Физики – 2 семестра
1 – й семестр
Лекции
лабораторные работы + практика (решение задач)
К экзамену по физике допускаются те, кто сдавал лабораторные работы и
задачи по практике.
Обязательное условие получения зачёта – выполнение всех лабораторных
работ.
Если не сданы задачи, то на экзамен выносится одна или несколько (по
разным темам) дополнительные задачи.
Экзамен : два вопроса и одна задача.
Экзамен сдаётся лектору.
Если экзамен не сдан, предоставляется 2 попытки пересдачи.
При второй пересдаче, экзамен сдаётся комиссии.

3.

Методические и учебные пособия
+
Рекомендуемые учебники
Учебные пособия
Сайт КГТУ–
Методические материалы Литература

4.

f (t )
f
- изменение f
df
- бесконечно малое изменение f
Оператор
дифференцирования
df
d
f (t ) [ f (t )]
dt
dt
1. Производная
2. Отношение df к dt

5.

КЛАССИЧЕСКАЯ МЕХАНИКА
(Механика – раздел физики, посвященный
изучению простейшей формы движения
материальных
тел:
перемещение
тел
относительно друг друга)
И. Ньютон
(1643 – 1727)
Макромир
. 8
V << C = 3 10
Описание механического движения
м/с
Г. Галилей
(1564 – 1642)
Система отсчёта
Система отсчета : совокупность системы координат связанной с телом,
по отношению к которому изучается движение других тел и часов.
Например: система отсчёта может быть связана с Землей, Солнцем.
Основная задача механики:
Eсли известно механическое состояние системы (совокупность координат
и скоростей) в момент времени t0 , определить механическое состояние
системы в момент времени t>t0

6.

Всякое движение твердого тела может быть представлено как сумма
поступательного и вращательного движений.
Поступательное движение –
движение тела, при котором
прямая, соединяющая две любые
точки тела, остается параллельной
самой себе при движении этого
тела.
Следствие.
Все
движутся
по
траекториям.
точки
тела
одинаковым
Вращательное движение твердого
тела вокруг оси – движение тела, при
котором все точки тела описывают
окружности
в
плоскостях,
перпендикулярных к оси вращения и с
центрами, лежащими на этой оси.

7.

1. Кинематика
1.1. Характеристики кинематики материальной точки
Для описания движения материальной точки будем
использовать декартову прямоугольную систему
координат (x,y, z).
i , j , k – орты, единичные векторы, задающие
направление вдоль осей x, y и z соответственно;
i j k 1
r (t ) – радиус-вектор:
вектор, проведенный из начала системы координат в рассматриваемую точку и
характеризующий положение точки в пространстве в момент времени t.
r (t ) x(t )i y(t ) j z(t )k
r r x y z
2
2
2
2
2

8.

Пусть материальная точка движется по
некоторой траектории.
t1
z
Траектория
–
линия,
описываемая
материальной точкой при ее движении в
пространстве.
r1
k
– радиус-вектор, характеризующий
положение точки в пространстве в момент
времени t1.
r2
i
t2
r2
y
j
x
- радиус-вектор, характеризующий положение точки в момент t2.
r12 r2 r1
ΔS -
– вектор перемещения м.т. за время
r12 S
Но lim r12 lim S
t 0
t t2 t1
путь, пройденный материальной точкой, или длина траектории.
В общем случае
dr
r1
dS
dr12
t 0
dr dS
- элементарное перемещение, вектор направлен по касательной к
траектории движения (бесконечно малый, нельзя нарисовать).

9.

dr
dt
мгновенная (истинная) скорость, характеризующая быстроту
изменения положения материальной точки в пространстве;
Вектор скорости направлен по касательной к
траектории движения;
r xi yj zk
dr d ( xi yj zk ) dx dy dz
i
j k xi y j z k
dt
dt
dt
dt
dt
Модуль мгновенной скорости
dr dS
dt
dt
Средняя скорость
d
a
dt
x2 y2 z2
S
vср
t
мгновенное (истинное) ускорение, характеризующее быстроту
изменения вектора скорости материальной точки.

10.

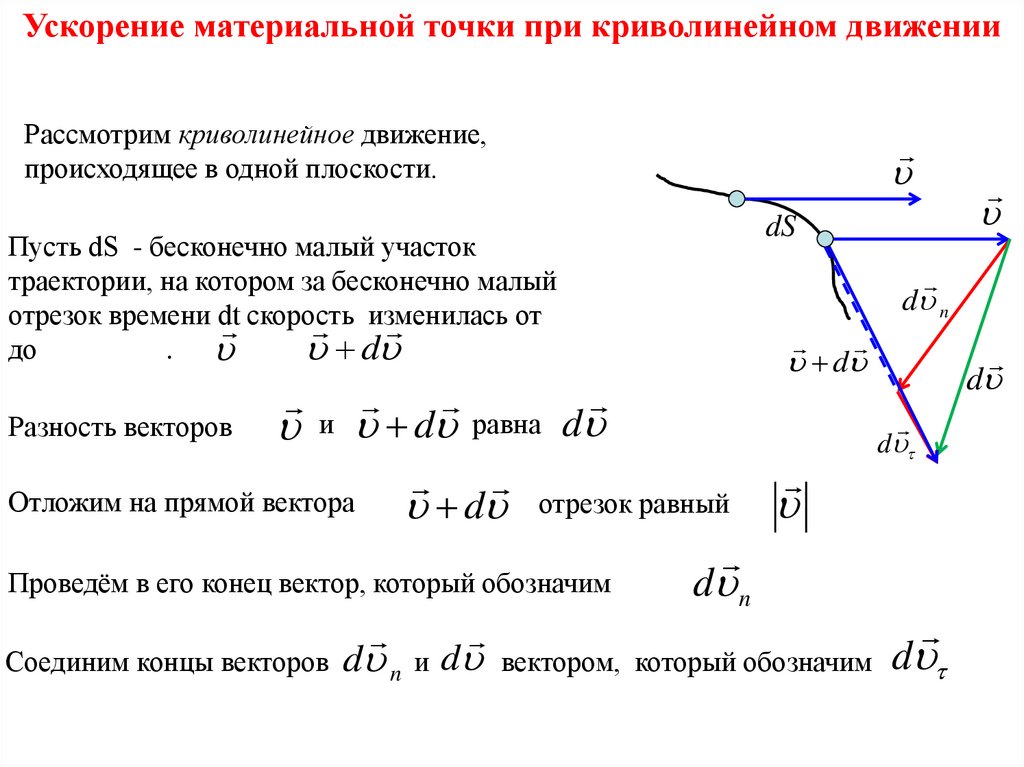
Ускорение материальной точки при криволинейном движении
Рассмотрим криволинейное движение,
происходящее в одной плоскости.
Разность векторов
и
d
равна
d
Отложим на прямой вектора
d n
Соединим концы векторов
d n
и
d
d
d
отрезок равный
Проведём в его конец вектор, который обозначим
dS
Пусть dS - бесконечно малый участок
траектории, на котором за бесконечно малый
отрезок времени dt
от
скорость
изменилась
до
.
d
d
d
d n
вектором, который обозначим
d

11.

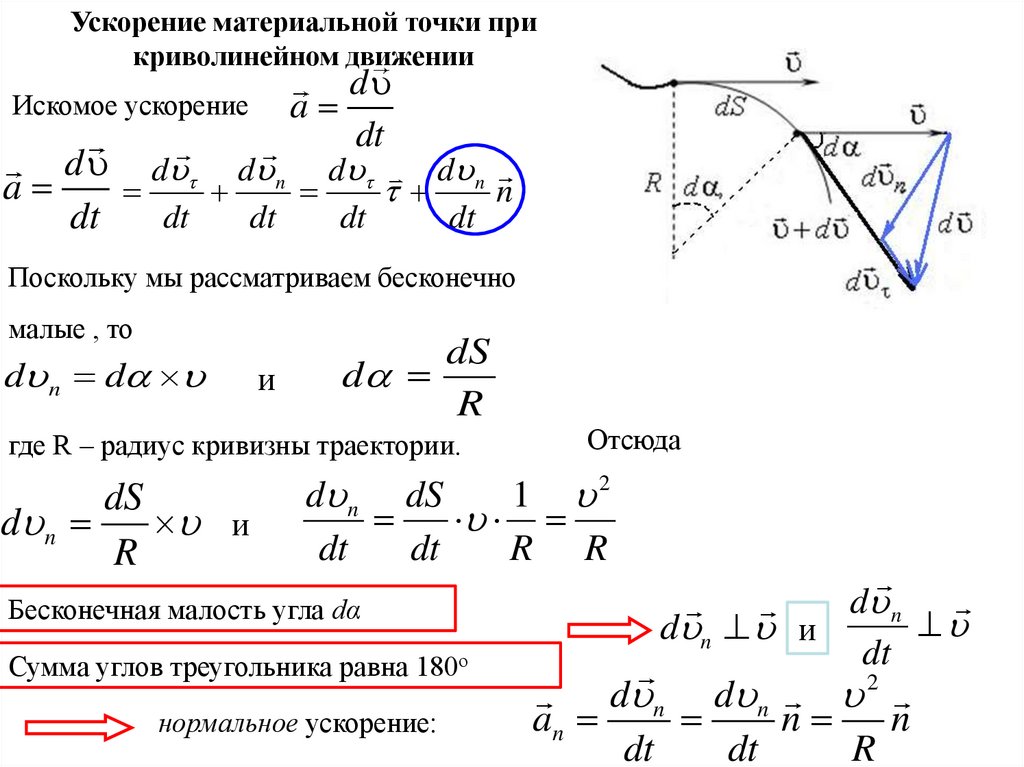
Ускорение материальной точки при криволинейном движении
d
a
dt
Искомое ускорение
Можно видеть, что
d d n d
d d d n d d n
a
n
dt
dt
dt
dt
dt
и n
единичные вектора,
направленные вдоль
d
d и d n
- приращение длины вектора скорости
Назовём эту составляющую ускорения тангенциальной:
d d
dt
dt
d
a
dt
Тангенциальное ускорение совпадает с направлением скорости (с касательной к
траектории) и отвечает за изменение модуля скорости.

12.

Ускорение материальной точки при
криволинейном движении
d
Искомое ускорение a
dt
d d d n d d n
a
n
dt
dt
dt
dt
dt
Поскольку мы рассматриваем бесконечно
малые , то
d n d
и
dS
d
R
где R – радиус кривизны траектории.
dS
d n
и
R
Отсюда
d n dS
1 2
dt
dt
R R
Бесконечная малость угла dα
Сумма углов треугольника равна 180о
нормальное ускорение:
d n
d n и
dt
2
d n d n
an
n
n
dt
dt
R

13.

Нормальное ускорение:
d n d n 2
an
n
n
dt
dt
R
Характеризует быстроту изменения направления
вектора скорости.
Тангенциальное ускорение
d
a
dt
характеризует быстроту изменения модуля скорости.
Полное ускорение при криволинейном движении
a a an
a a a
2
d 2
a
n
dt
R
2
n
const
d
При равномерном движении по окружности:
a
0 a an
dt
2
R an
0 a a
При прямолинейном движении:
R

14.

Поступательное движение – Все точки тела
движутся по одинаковым траекториям.
Для описания поступательного движения
тела, достаточно рассмотреть движение
одной точки тела, например, его центра масс.
Материальная точка:
тело, формой и размерами которого можно пренебречь в условиях
данной задачи.
Пример: Земля при её движении вокруг Солнца.

15.

Кинематика вращательного движения

16.

Всякое движение твердого тела может быть представлено как сумма
поступательного и вращательного движений.
Поступательное
движение
–
движение тела, при котором
прямая, соединяющая две любые
точки тела, остается параллельной
самой себе при движении этого
тела.
Следствие.
Все
движутся
по
траекториям.
точки
тела
одинаковым
Вращательное движение твердого
тела вокруг оси – движение тела, при
котором все точки тела описывают
окружности
в
плоскостях,
перпендикулярных к оси вращения и с
центрами, лежащими на этой оси.

17.

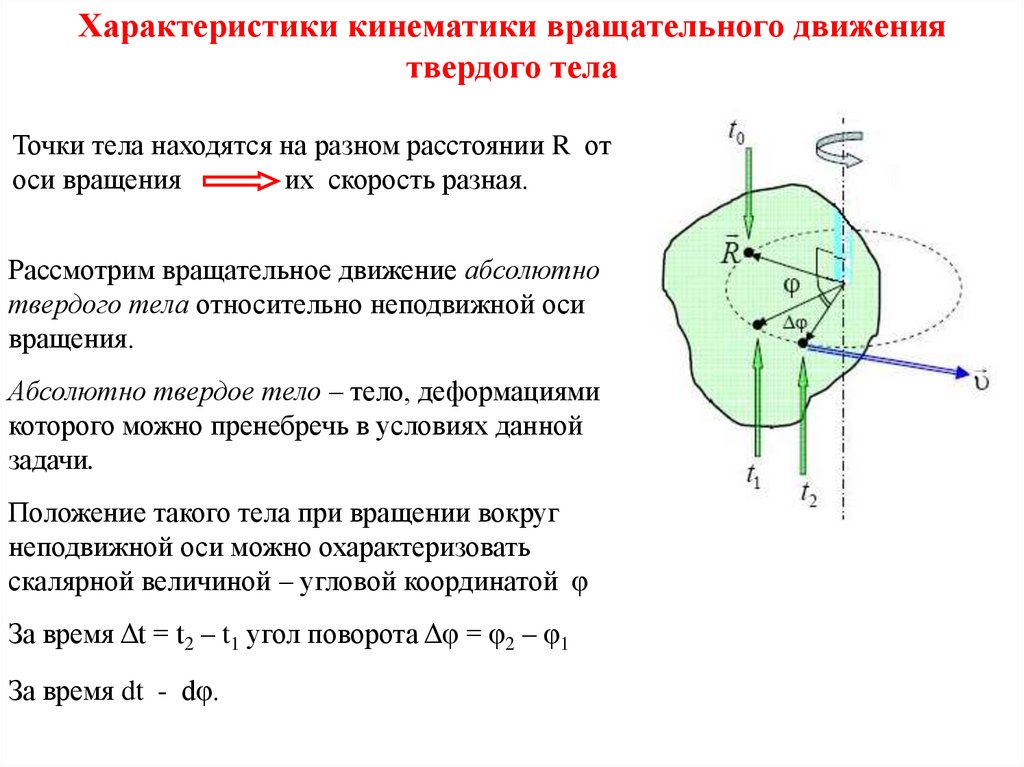
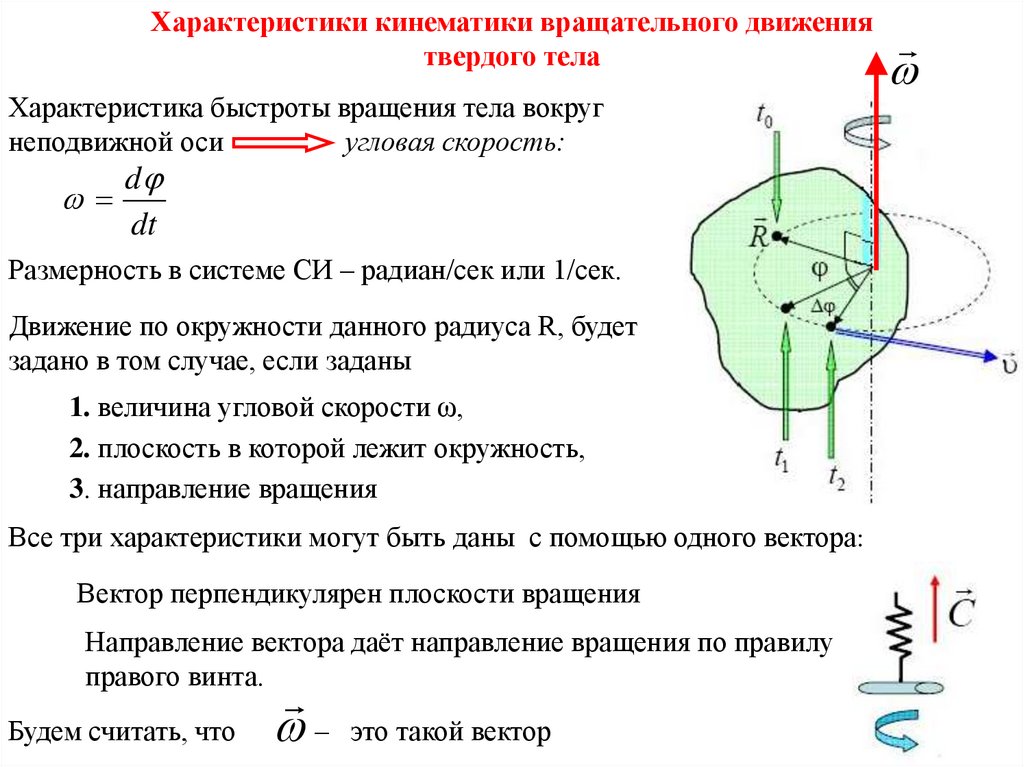
Характеристики кинематики вращательного движения
твердого тела
Точки тела находятся на разном расстоянии R от
оси вращения
их скорость разная.
Рассмотрим вращательное движение абсолютно
твердого тела относительно неподвижной оси
вращения.
Абсолютно твердое тело – тело, деформациями
которого можно пренебречь в условиях данной
задачи.
Положение такого тела при вращении вокруг
неподвижной оси можно охарактеризовать
скалярной величиной – угловой координатой φ
За время Δt = t2 – t1 угол поворота Δφ = φ2 – φ1
За время dt - dφ.

18.

Характеристики кинематики вращательного движения
твердого тела
Характеристика быстроты вращения тела вокруг
неподвижной оси
угловая скорость:
d
dt
Размерность в системе СИ – радиан/сек или 1/сек.
Движение по окружности данного радиуса R, будет
задано в том случае, если заданы
1. величина угловой скорости ω,
2. плоскость в которой лежит окружность,
3. направление вращения
Все три характеристики могут быть даны с помощью одного вектора:
Вектор перпендикулярен плоскости вращения
Направление вектора даёт направление вращения по правилу
правого винта.
Будем считать, что
–
это такой вектор

19.

Характеристики кинематики вращательного движения
твердого тела
При вращении с постоянной угловой скоростью полный оборот совершается за
время
T
2
2
T
Т – период обращения.
Величина обратная периоду – число оборотов в единицу времени:
1
T 2
2
Т и можно рассматривать и как характеристики движения с переменной
угловой скоростью. Тогда они будут характеризовать вращение в данный момент
времени.
Пример: изменение скорости вращения ротора, двигателя и т.п. характеризуют
изменением числа оборотов (а не изменением угловой скорости).

20.

Характеристики кинематики вращательного движения
твердого тела
Угловое ускорение - характеристика
быстроты изменения угловой скорости
d
.
dt
При неподвижной оси вращения и
совпадают по направлению в случае
ускоренного вращательного движения.
В случае замедленного вращательного
движения и - противоположны.

21.

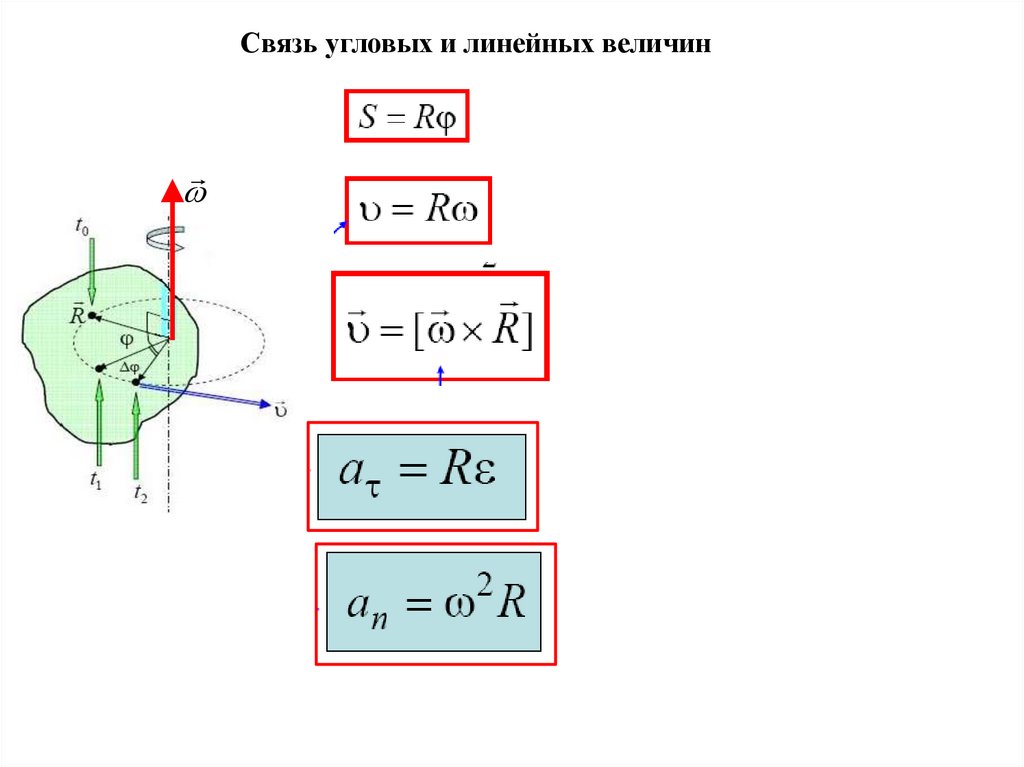
Связь угловых и линейных величин
Путь, пройденный точкой при движении по окружности:
S R
Связь между модулями линейной скорости точки тела и угловой скоростью:
v
dS d ( R )
d
R
R
dt
dt
dt
v R
Связь между модулями тангенциального ускорения точки тела и углового
ускорения:
d ( R) R d
dv
R
a
dt
dt
dt
.
a R
Связь между модулем нормального ускорения точки тела и модулем
угловой скорости:
v2
an
2R
R

22.

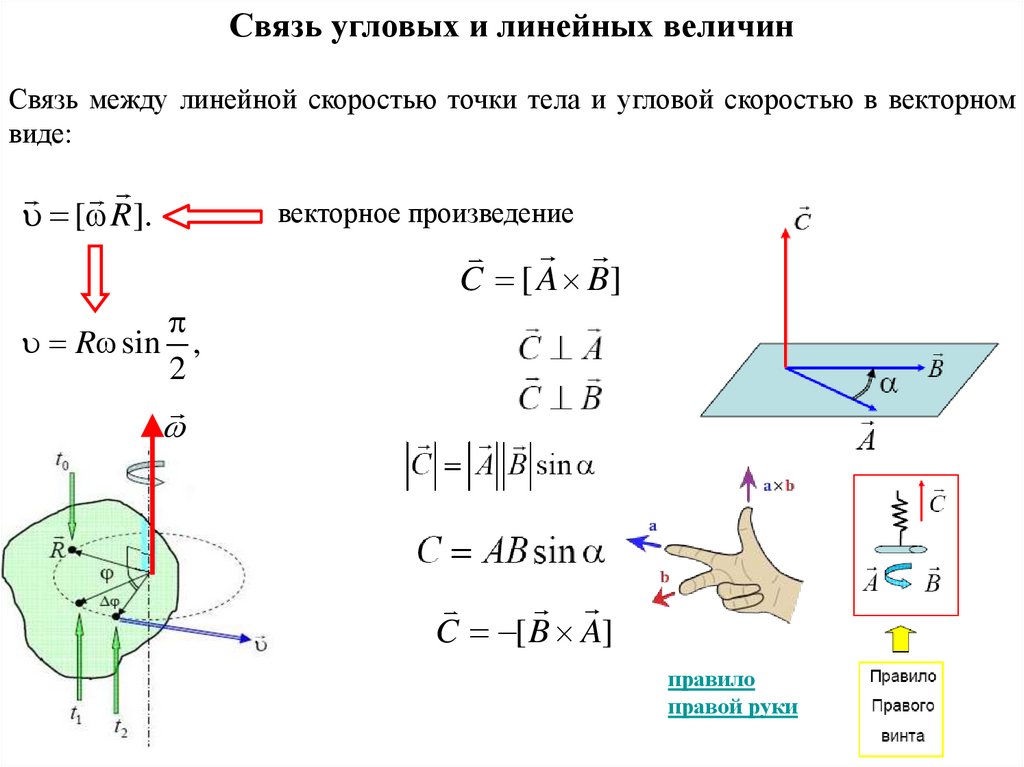
Связь угловых и линейных величин
Связь между линейной скоростью точки тела и угловой скоростью в векторном
виде:
[ R ].
векторное произведение
C [ A B]
R sin ,
2
.
C [ B A]
правило
правой руки

23.

Связь угловых и линейных величин

24.

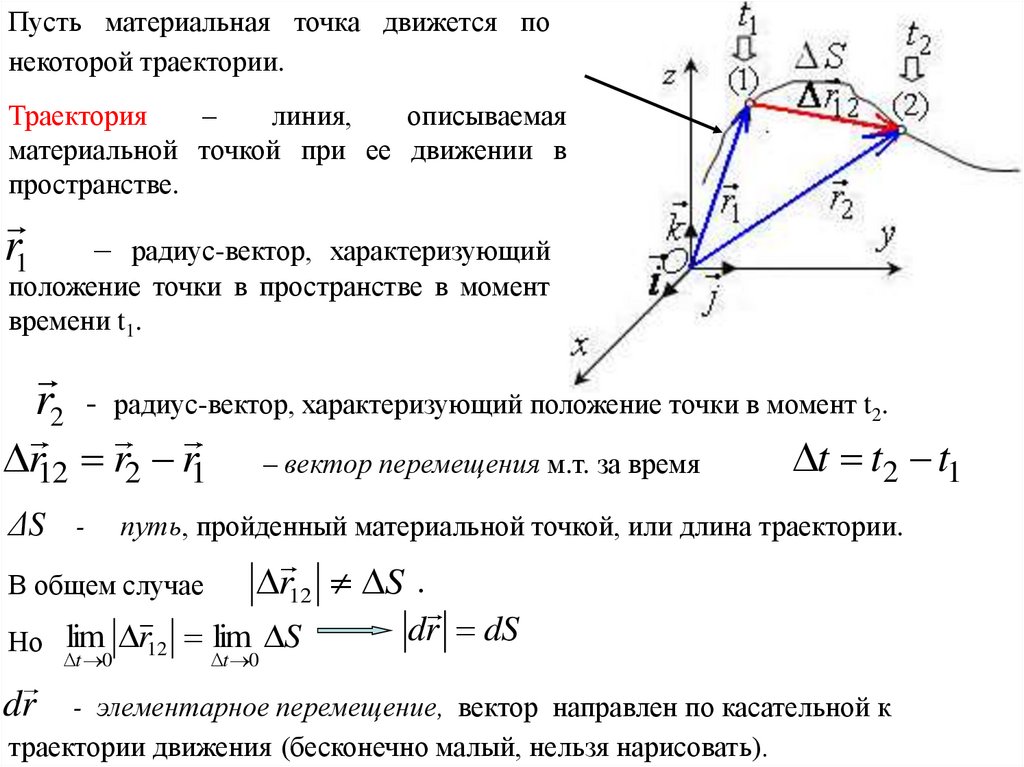
Пусть материальная точка движется по
некоторой траектории.
Траектория
–
линия,
описываемая
материальной точкой при ее движении в
пространстве.
r1
– радиус-вектор, характеризующий
положение точки в пространстве в момент
времени t1.
r2
- радиус-вектор, характеризующий положение точки в момент t2.
r12 r2 r1
ΔS -
– вектор перемещения м.т. за время
t t2 t1
путь, пройденный материальной точкой, или длина траектории.
r12 S .
В общем случае
dr dS
Но lim r12 lim S
t 0
dr
t 0
- элементарное перемещение, вектор направлен по касательной к
траектории движения (бесконечно малый, нельзя нарисовать).