Методы проецирования. Общие положения

1.

КАФЕДРА ИНЖЕНЕРНОГО ПРОЕКТИРОВАНИЯ
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

2.

ДОЦЕНТ
ПОНОМАРЕНКО ЕВГЕНИЙ АНАТОЛЬЕВИЧ

3.

ЛЕКЦИЯ 1
МЕТОДЫ ПРОЕЦИРОВАНИЯ
ОБЩИЕ ПОЛОЖЕНИЯ
Инженерная графика (ИГ) – построение
изображений плоских или объемных предметов
с помощью проецирования.

4.

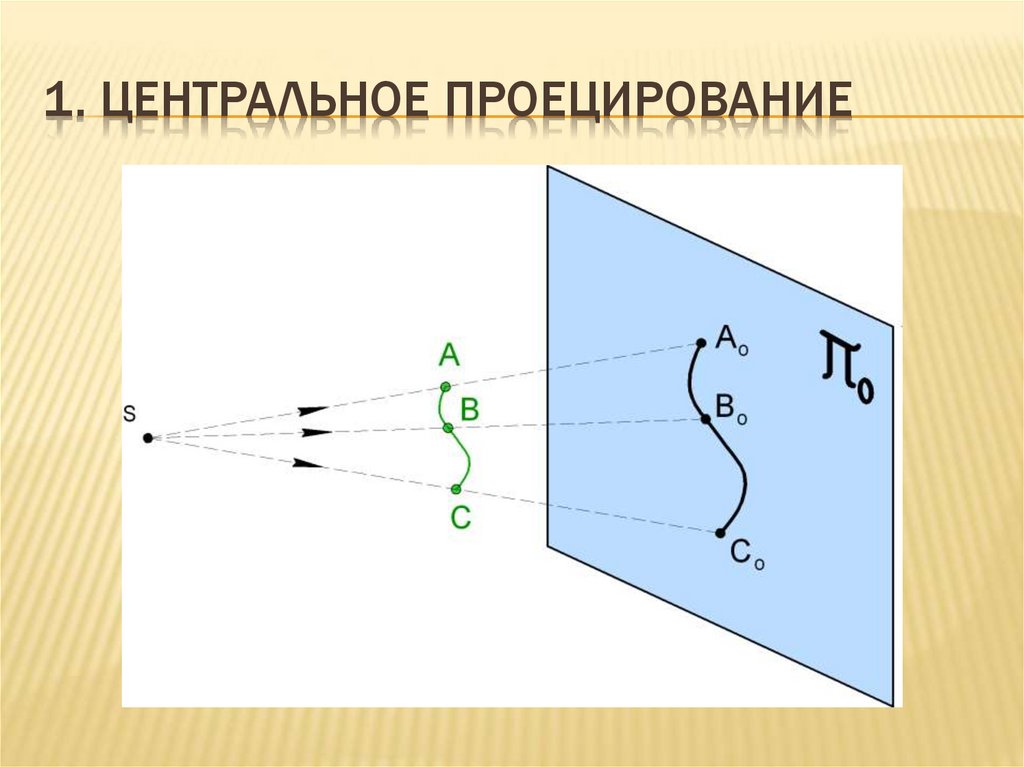
1. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ

5.

Дано:
1. Кривая ABC
2. Плоскость πо
3. Точка S
Из (•) S проведем проецирующие лучи
через (•)(•)A,B,C до пересечения с
плоскостью πо.
Получим (•)(•) AоBоCо.

6.

Эти элементы:
(•) S – полюс (центр) проекция, где
πо – плоскость проекции.
SAо, SBо, SCо – проецирующие лучи.
ABC – оригинал.
AоBоCо – центральная проекция ABC
на πо

7.

Свойства центрального
проецирования:
1. Любой геометрический элемент имеет на
плоскости πо только одну проекцию.
2. Любая (•) на плоскости πо - есть проекция
бесконечного числа (•) на луче.
3. Проекция прямой линии - прямая.
Это называется перспективой и применяется
в архитектуре, живописи.

8.

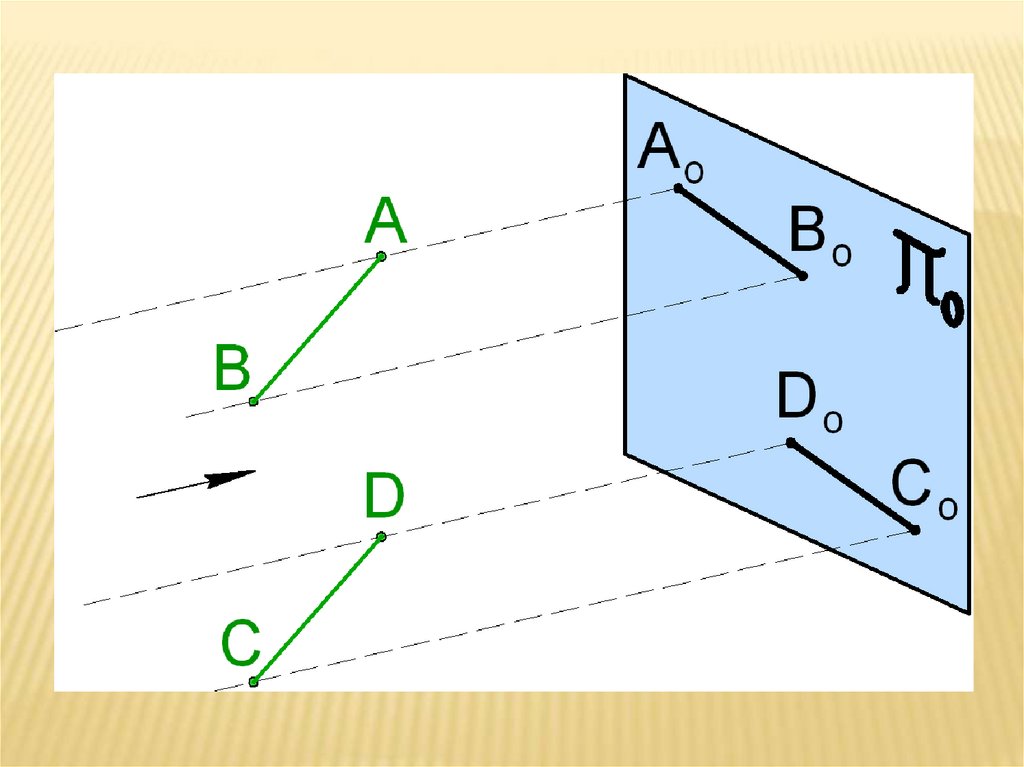
2. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ

9.

Это проецирование с помощью
параллельных лучей, т.е. S находится
в ∞.
ABC – оригинал.
AоBоCо – проекция ABC на p о.
Свойства те же, что и у центрального
проецирования, кроме того:

10.

11.

Если
AB // CD, то AоBо // CоDо
Если лучи не перпендикулярны к плоскости
проекции, то косоугольное проецирование
Если лучи перпендикулярны к плоскости
проекции, то прямоугольное (ортогональное)
проецирование.
Оно в основе всех чертежей.

12.

3. ПРОЕЦИРОВАНИЕ НА ПЛОСКОСТИ
КООРДИНАТ
Плоскости располагают так:
одна – горизонтальная, две – вертикальные
Пусть даны оси прямоугольной системы координат.
Плоскость
XOY- горизонтальная –
Плоскость
XOZ- вертикальная –
Плоскость YOZ-
профильная –
π1
π2
π3

13.

14.

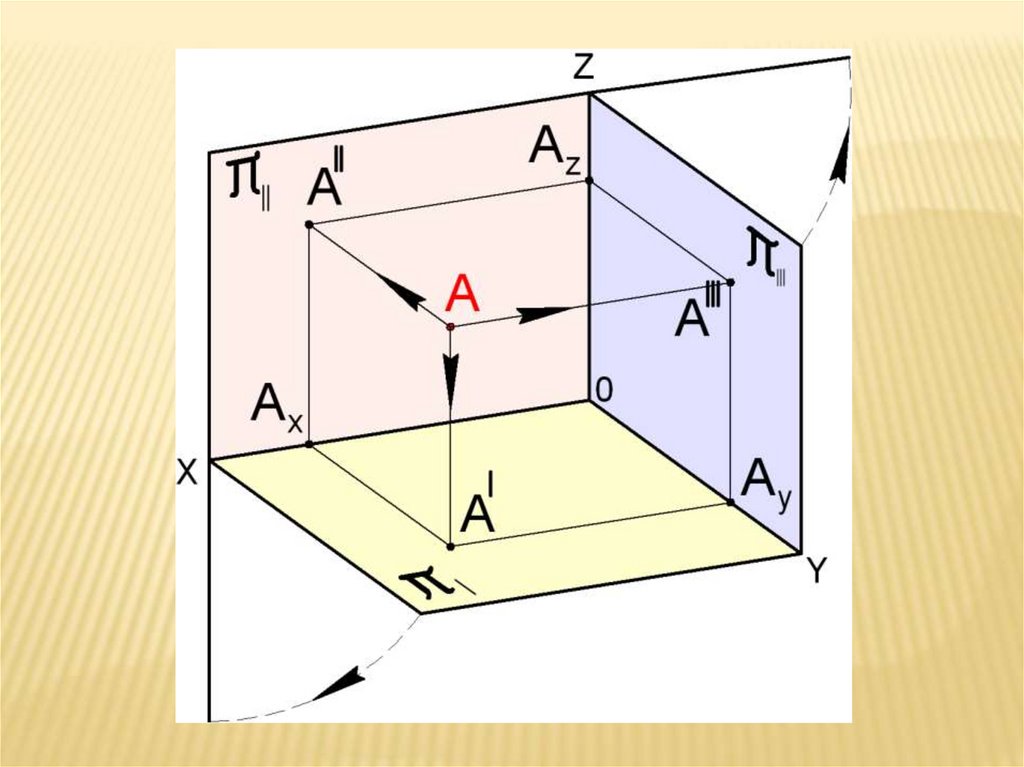
Возьмем (•) A и спроецируем на плоскости
координат. Получим А‫׀‬, А‫׀׀‬А‫ ׀׀׀‬на
π3 соответственно.
А ‫׀‬- горизонтальная проекция Ax
А ‫׀׀‬- вертикальная проекция Az
А‫ ׀׀׀‬- профильная проекция Ay
Ax Ay Az координаты (•) A
π1, π2 и

15.

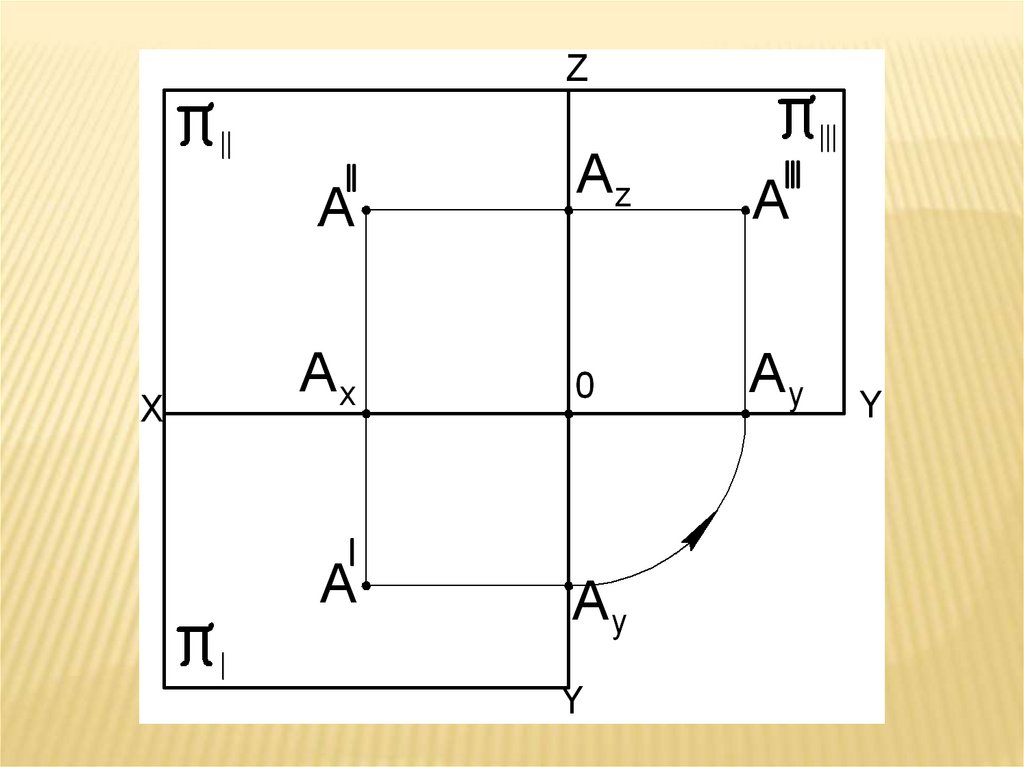
Развернем этот чертеж на плоскость
π2.
Получим комплексный чертеж (•) A или эпюр
Монжа (эпюр).
Этот эпюр однозначно фиксирует положение
(•) A в пространстве. При этом:

16.

17.

ОЧЕНЬ ВАЖНО
А ‫׀‬и А ‫׀׀‬всегда на одной вертикали и
перпендикулярно OX
А ‫ ׀׀‬А ‫׀׀׀‬всегда на одной горизонтали и
перпендикулярно OZ
Для определения положения (•) A
достаточно две проекции. В общем случае
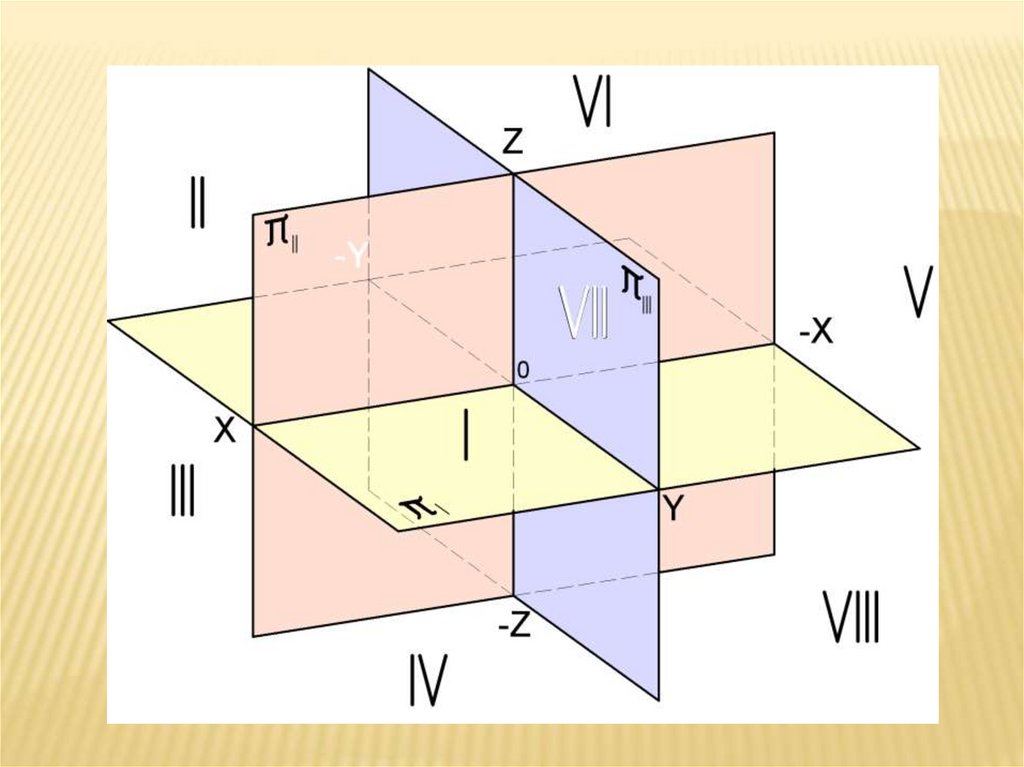
π1, π2 , π3 делят пространство на 8 частей –
октантов.

18.

19.

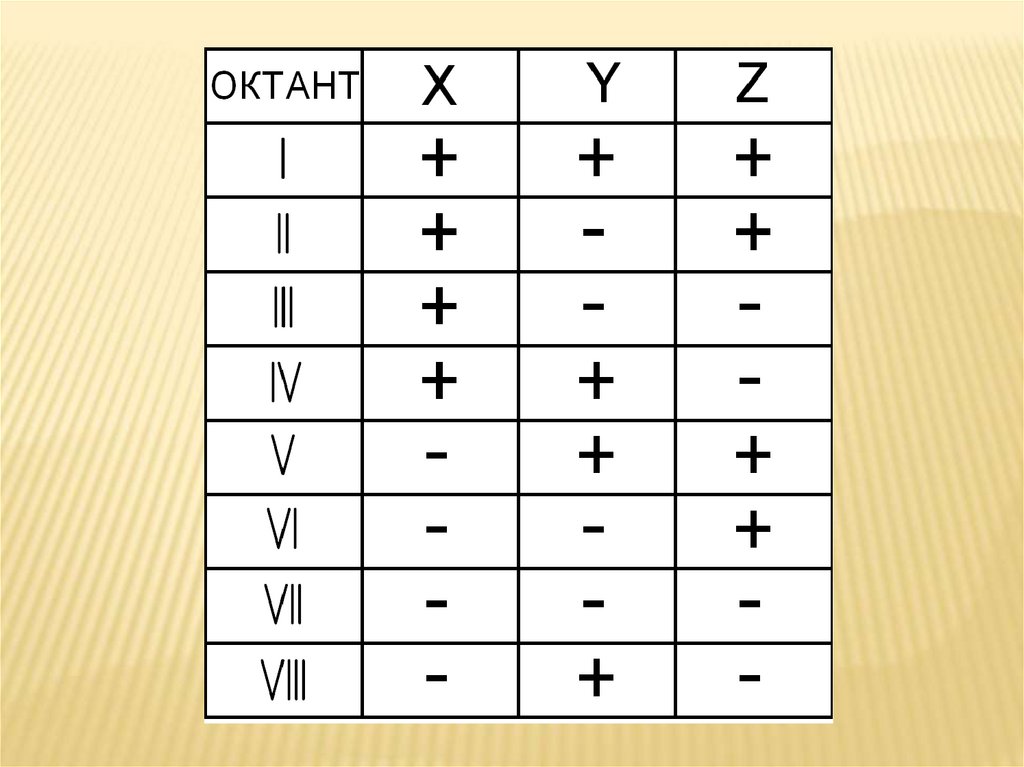
Нумерация октантов принята римскими
цифрами всего октантов восемь.
В общем случае (•) может быть в любом
октанте. В зависимости от знака координат
X,Y, Z можно определить положение (•) в
конкретном октанте:

20.

21.

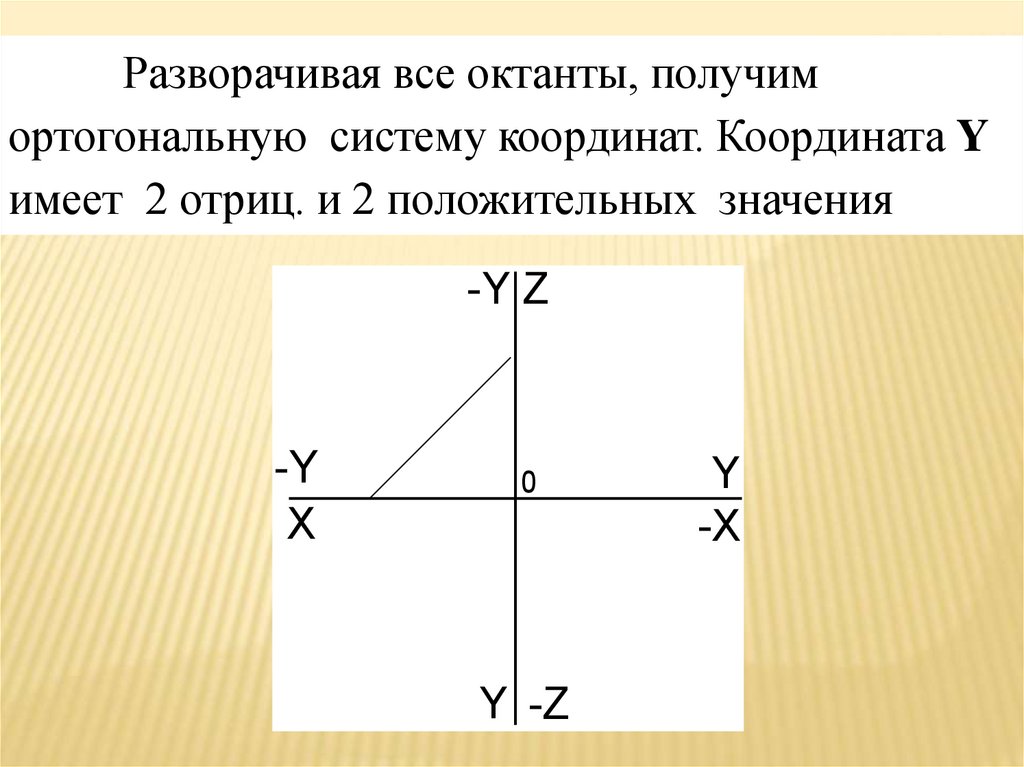
Разворачивая все октанты, получим
ортогональную систему координат. Координата Y
имеет 2 отриц. и 2 положительных значения
-Y Z
-Y
Х
0
Y -Z
Y
-Х

22.

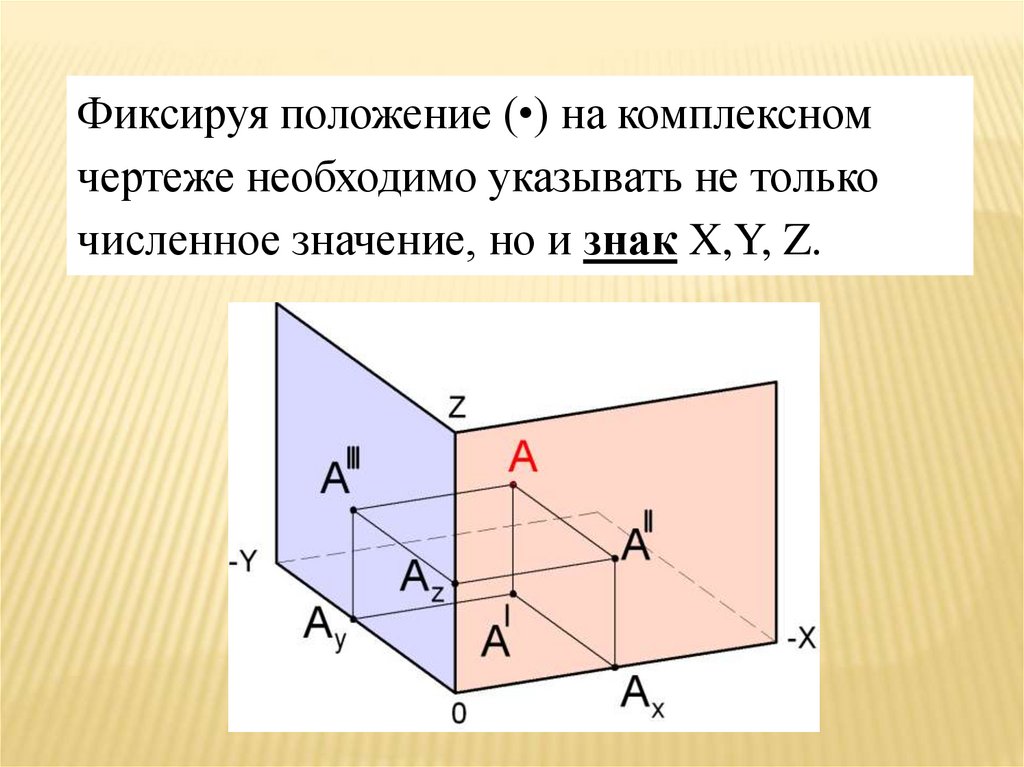
Фиксируя положение (•) на комплексном
чертеже необходимо указывать не только
численное значение, но и знак X,Y, Z.

23.

24.

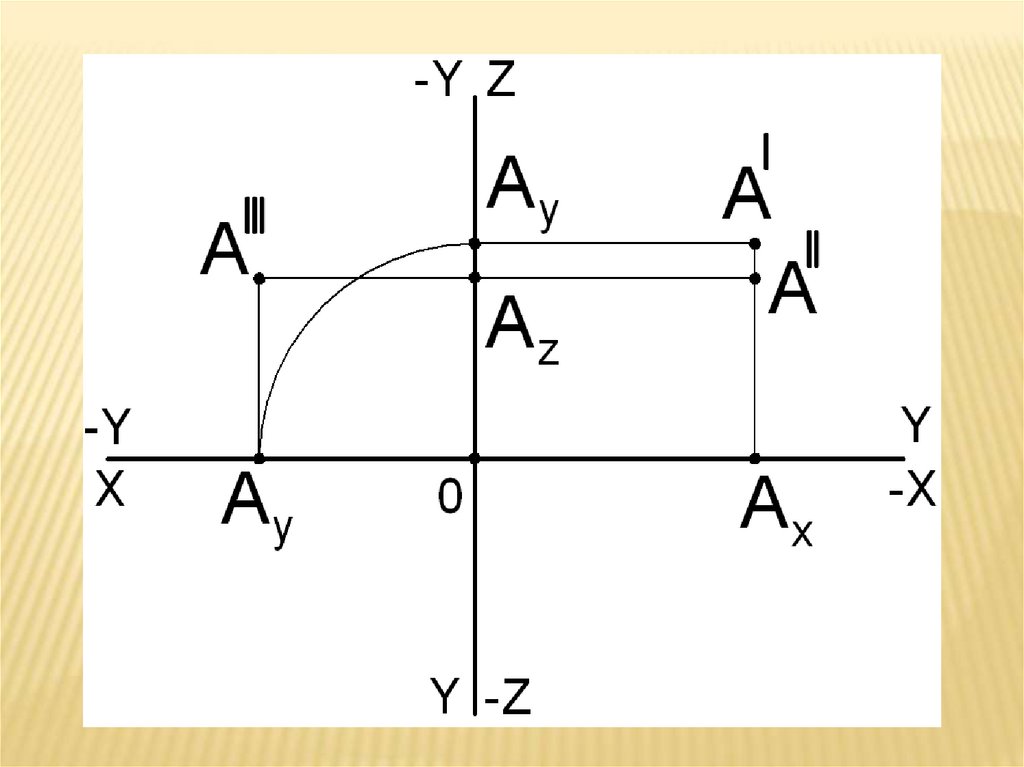
В данном случае (•) A – точка общего
положения, т.к. X,Y, Z ≠ 0.
Рассмотрим (•)(•) частного положения.
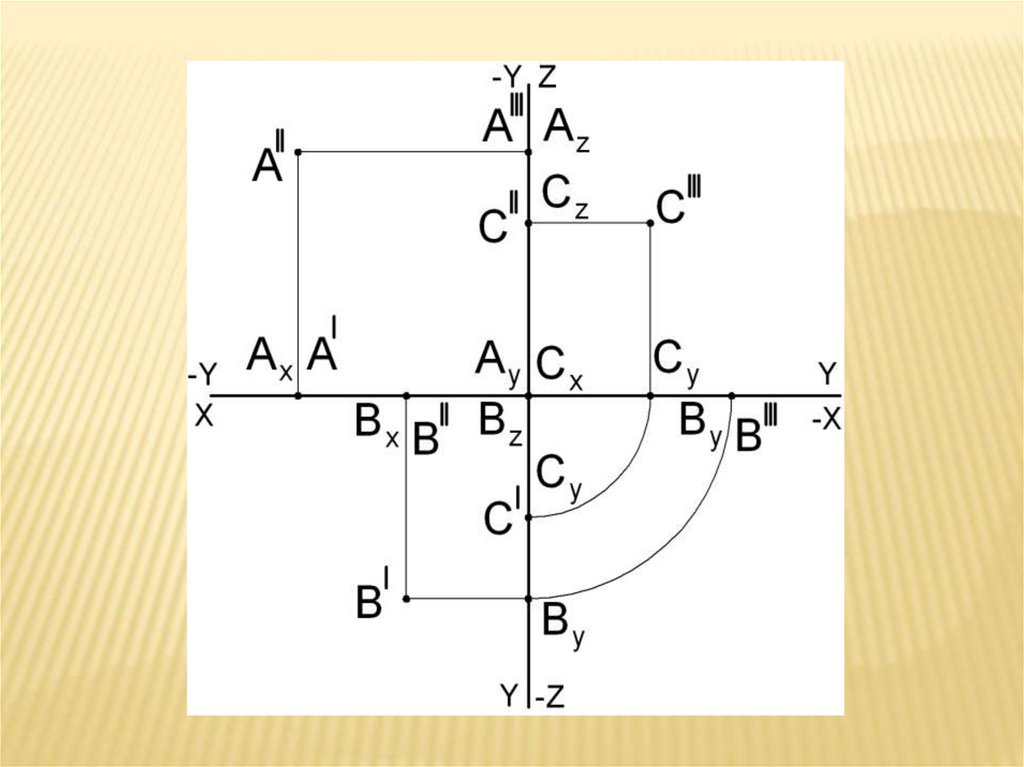
1. Точка в плоскости координат
Одна координата равна 0.

25.

26.

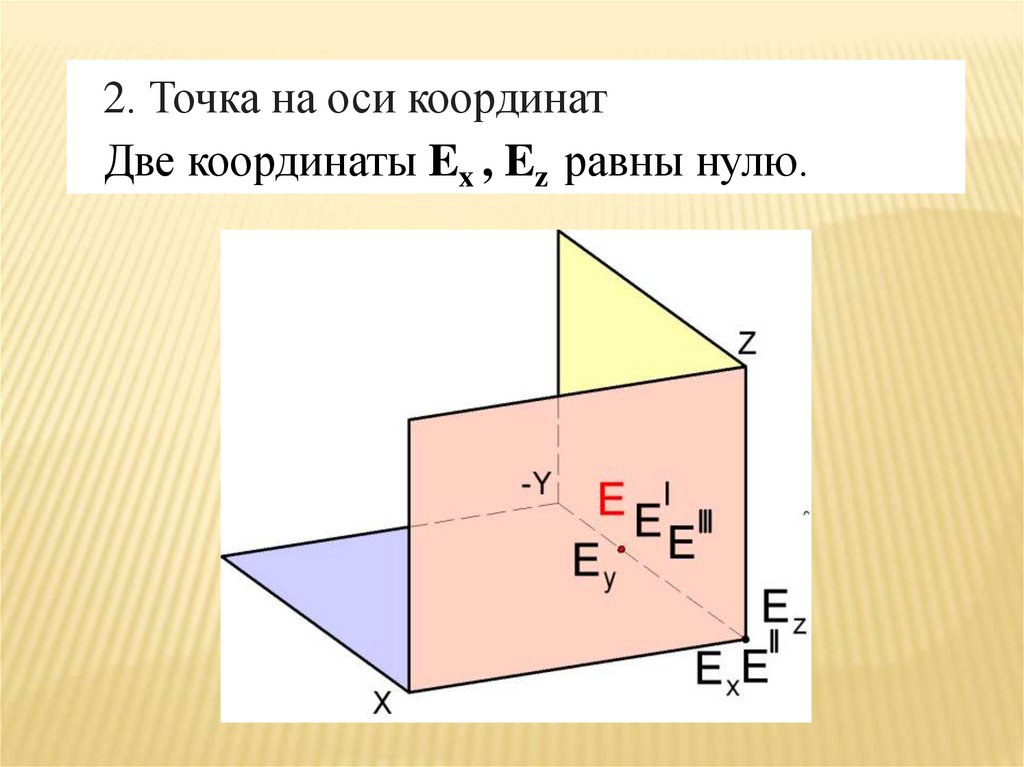
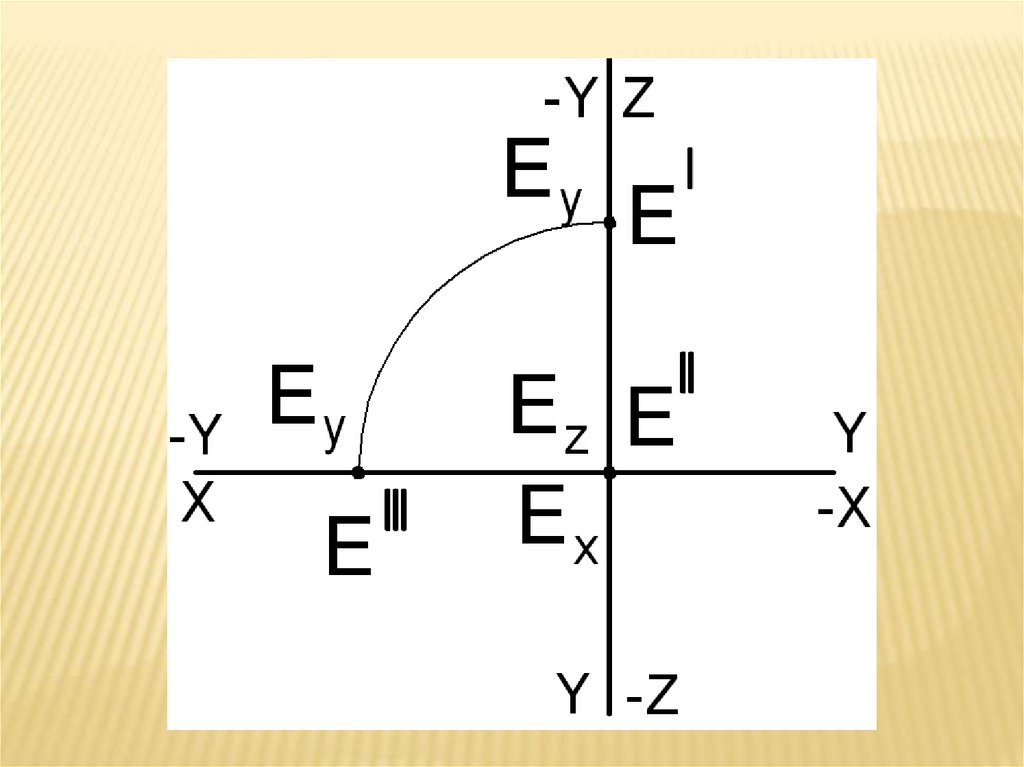
27.

2. Точка на оси координат
Две координаты Ex , Ez равны нулю.