Похожие презентации:
Механика твердого тела. Тема 4
1.
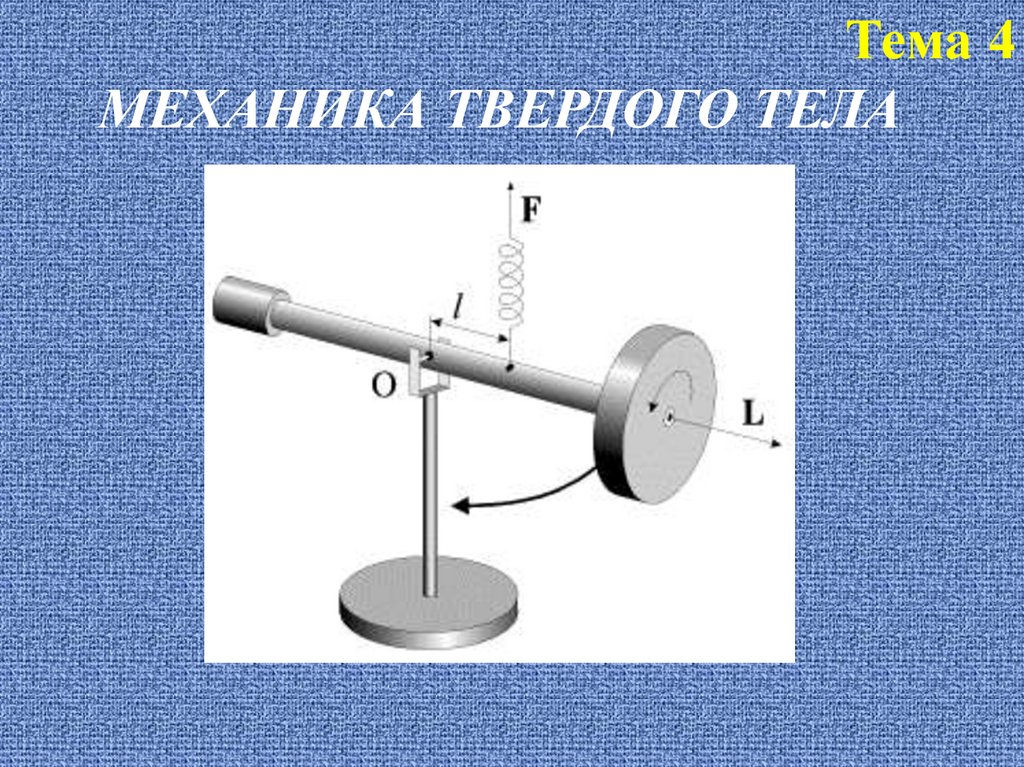
Тема 4МЕХАНИКА ТВЕРДОГО ТЕЛА
2.
План лекции1. МЕХАНИКА ТТ. Момент инерции.
2. Кинетическая энергия вращения.
3. Момент силы. Уравнение динамики
вращательного движения.
4. Момент импульса. Закон сохранения момента
импульса.
5. Деформации твердого тела.
3.
Момент инерцииМоментом инерции системы (тела) относительно
данной оси называется физическая
.
величина, равная сумме произведений масс m материальных точек системы на квадрат
n
расстояния до оси (дискретное распределение точек):
I mi ri 2 .
i 1
В случае непрерывного распределения масс сумма сводится к интегралу:
m
I r 2 dm.
0
Если известен момент инерции тела относительно оси, проходящей через его центр масс,
то момент инерции относительно любой другой параллельной оси определяется теоремой
Гюйгенса-Штейнера: момент инерции тела I относительно произвольной оси равен
моменту инерции Ic относительно параллельной оси, проходящей через центр масс С тела,
сложенному с произведением массы m тела на квадрат расстояния а между осями:
I I c ma 2 .
Моменты инерции некоторых тел
1
Шар (ось вращения проходит через центр)
Iш
2
mR 2
5
2
Сплошной цилиндр, диск (ось вращения проходит через центр)
Iд
1
mR 2
2
3
Полый цилиндр (ось вращения проходит через центр)
4
Стержень (ось вращения проходит через середину)
5
Стержень (ось вращения проходит через конец)
I ц mR 2
1
ml 2
12
1
I с m 2
3
Ic
4.
Кинетическая энергия вращенияРассмотрим абсолютно ТТ, вращающееся около неподвижной оси Z, проходящей через
.
него. Кинетическая энергия поступательного движения
тела:
mi i2
T
.
2
i 1
n
Используя формулу = R, получим
n
Tвр
i2 mi
I z 2
ri
mi ri
,
2
2 i 1
2
i 1
Iz– момент инерции ТТ относительно оси Z.
Таким образом, кинетическая энергия вращающегося тела:
Сравнивая формулы
Eпост
m 2
I 2
и Твр
,
2
2
2
2
n
2
I 2
Твр
.
2
можно сделать вывод, что физический смысл момента инерции – мера инертности тела
при вращательном движении.
В случае плоского движения тела, энергия движения складывается:
Ek
m 2
2
I 2
2
.
Плоское движение – движение, когда тело совершает одновременно поступательное и
вращательное движение.
5.
Примеры плоского движения6.
Момент силы. Уравнение динамики вращательного движениятвердого тела
Моментом силы F относительно неподвижной точки О называется физическая величина,
определяемая векторным произведением радиуса - вектора r, проведенного
из точки О в
точку А приложения силы, на силу F:
M [r , F ]
M r F,
или
М – псевдовектор, его направление совпадает с направлением поступательного движения
правого винта при его вращении от r к F (рис.1). Модуль момента силы
M rF sin Fl , (1)
α - угол между r и F,
силы – кратчайшее расстояние
r sin - плечо
между линией действия силы и т. О.
Работа при вращении тела равна произведению проекции силы
на направление смещения на величину смещения
dA Fr sin d .
Учитывая (1), можно записать:
dA M z d
где M z - момент силы относительно неподвижной оси Z.
С другой стороны, работа при вращении тела идет на увеличение
Рис. 1
кинетической энергии:
d
d
I z 2
dA dEк , но dEк d
I z
.
I z d ; dA M z d I z d , M z
dt
dt
2
d
d
,
получаем
M
I
I z .
Учитывая
z
z
dt
dt
M I .(2)
Уравнение (2) называется уравнением динамики вращательного движения твердого тела
относительно неподвижной оси.
7.
Момент импульса. Закон сохранения момента импульсаМоментом импульса материальной точки А относительно неподвижной точки О
называется физическая величина, определяемая векторным произведением:
L [r , p ] или
L r p,
r – радиус - вектор от т. О до т. А, p=m – импульс материальной точки, L – псевдовектор –
направлен в сторону поступательного движения правого винта при его вращении от r к p
(рис. 2). Модуль L: L rp sin rm sin p , r sin - плечо.
Моментом импульса ТТ относительно оси, называется величина
n
L mi i ri ,
i i r ,
при условии, что
получим
i 1
n
2
2
Lz mi ri mi ri I z , т.е. Lz I z .(3)
i 1
Таким образом, момент импульса ТТ относительно оси равен
произведению момента инерции
тела на угловую скорость.
Рис. 2
d
Продифференцируем формулу (3) по времени: dLz
dL z
dt
Iz
dt
I z M z
т.е.
dt
Mz
- это уравнение динамики вращательного движения твердого тела относительно
неподвижной оси: производная момента импульса ТТ относительно оси равна моменту сил
относительно той же оси. dL
0; L const
В замкнутой системе М=0, dt
- закон сохранения момента импульса.
Закон сохранения момента импульса: момент импульса замкнутой системы
сохраняется с течением времени.
8.
Поступательное движениеМасса
Скорость
m
dr
dt
d
Ускорение a
dt
Вращательное движение
Момент инерции
I mr 2
d
Угловая скорость
dt
Сила
F ma
Угловое ускорение d
dt
Момент силы M [r F ]
Импульс
p m
Момент импульса
Основное уравнение
динамики
F ma
2
Кинетическая энергия E m
k
2
L r p,
Lz I z
динамики
Основное уравнение
I z M z
Кинетическая энергия
Tвр
I 2
2
9.
Деформации твердого телаДеформа́ция (от лат. deformatio — «искажение») — изменение взаимного положения
частиц тела, связанное с их перемещением друг относительно друга. Деформация
представляет собой результат изменения межатомных расстояний и перегруппировки
блоков атомов. Обычно деформация сопровождается изменением величин межатомных
сил, мерой которого является упругое механическое напряжение.
Деформации разделяют на обратимые (упругие) и необратимые (пластические,
ползучести). Упругие деформации исчезают после окончания действия приложенных сил,
а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения
атомов металлов от положения равновесия (другими словами, атомы не выходят за
пределы межатомных связей); в основе необратимых — необратимые перемещения атомов
на значительные расстояния от исходных положений равновесия (то есть выход за рамки
межатомных связей, после снятия нагрузки переориентация в новое равновесное
положение).
Пластические деформации — это необратимые деформации, вызванные изменением
напряжений. Деформации ползучести — это необратимые деформации, происходящие с
течением времени. Способность веществ пластически деформироваться называется
пластичностью. При пластической деформации металла одновременно с изменением
формы меняется ряд свойств — в частности, при холодном деформировании
повышается прочность.
10.
Деформации твердого телаНаиболее простые виды деформации тела в целом:
растяжение-сжатие,
сдвиг,
изгиб,
кручение.
В большинстве практических случаев наблюдаемая деформация представляет собой
совмещение нескольких одновременных простых деформаций. В конечном счёте, любую
деформацию можно свести к двум наиболее простым: растяжению (или сжатию) и сдвигу.
Деформация называется упругой, если она исчезает после удаления вызвавшей её нагрузки
(то есть тело возвращается к первоначальным размерам и форме), и пластической, если
после снятия нагрузки деформация не исчезает (или исчезает не полностью).
Все реальные твёрдые тела при деформации в большей или меньшей мере обладают
пластическими свойствами. Твёрдое тело с достаточной точностью можно считать
упругим, то есть не обнаруживающим заметных пластических деформаций, пока нагрузка
не превысит некоторого предела (предел упругости).
Природа пластической деформации может быть различной в зависимости от температуры,
продолжительности действия нагрузки или скорости деформации. При неизменной
нагрузке, приложенной к телу, деформация изменяется со временем; это явление
называется ползучестью. С возрастанием температуры скорость ползучести
увеличивается.
11.
Деформации твердого тела12.
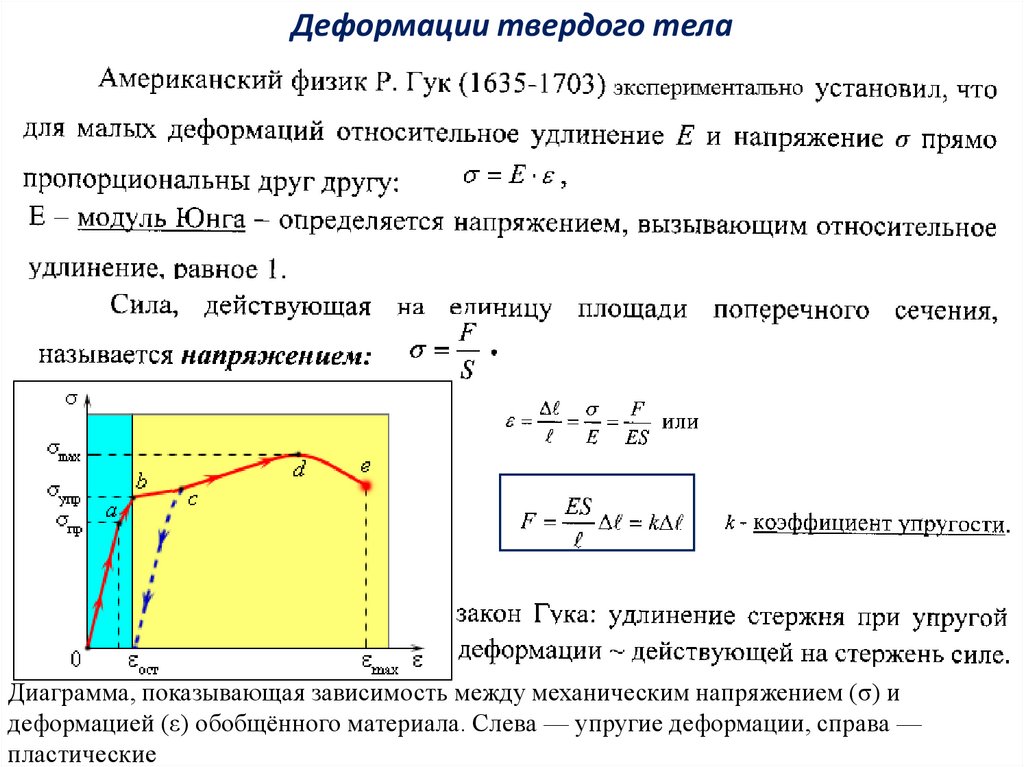
Деформации твердого телаДиаграмма, показывающая зависимость между механическим напряжением (σ) и
деформацией (ε) обобщённого материала. Слева — упругие деформации, справа —
пластические










 Физика
Физика








