Похожие презентации:
Механика твердого тела. (Лекция 4)
1. Механика твердого тела
лекция 42.
Физическим телом называетсясистема взаимодействующих частиц
массой Δmi и объемом ΔVi, непрерывно
заполняющих объем
V.
Абсолютно твердое тело (АТТ)
это система м.т. (частиц), расстояние
между которыми постоянно.
т.е. это тело, деформациями которого,
в условиях данной задачи, можно
пренебречь.
02
3. §§ Плоское движение
Поступательным называется движение,при котором любая из прямых,
связанных с двигающимся телом,
остается параллельной ее начальному
направлению.
Вращательным называется движение,
при котором все точки тела двигаются
по окружностям, центры которых лежат
на одной прямой, называемой осью
вращения.
03
4.
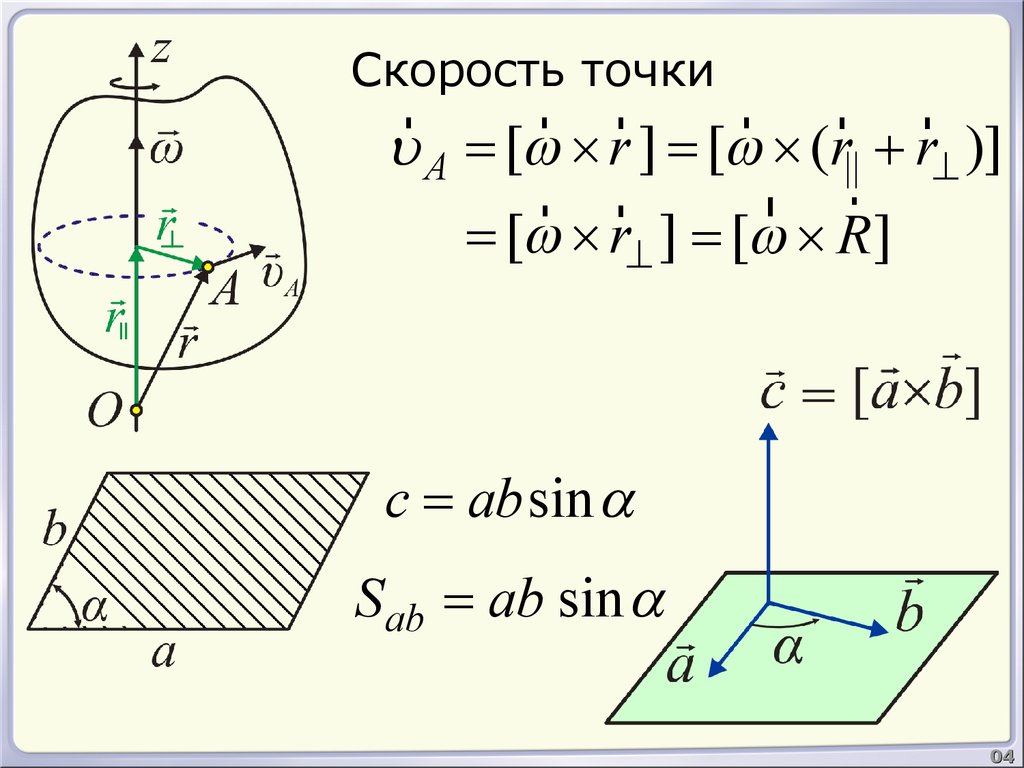
Скорость точкиr r r
r
r r
u A = [w ´ r ] = [w ´ (r|| + r^ )]
r r
r r
= [w ´ r^ ] = [w ´ R ]
c = ab sin a
Sab = ab sin a
04
5.
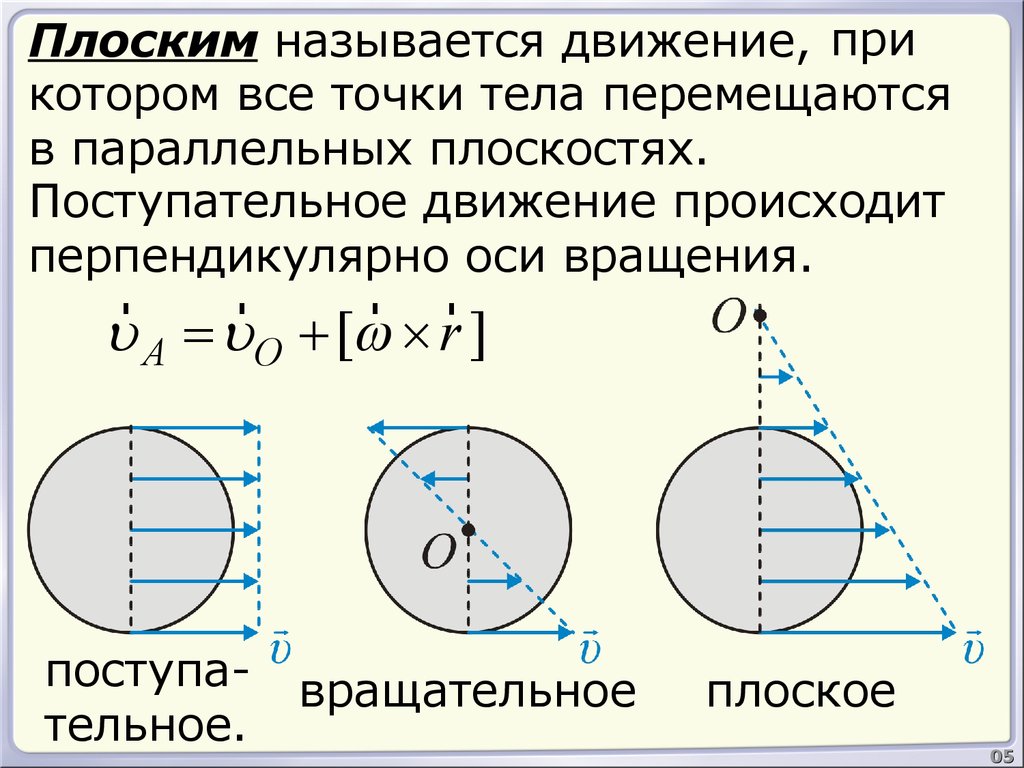
Плоским называется движение, прикотором все точки тела перемещаются
в параллельных плоскостях.
Поступательное движение происходит
перпендикулярно оси вращения.
r
r
r r
u A = uO + [w ´ r ]
поступательное.
вращательное
плоское
05
6.
При плоском движении т.т. может бытьпереведено из одного положения
в другое путем поворота относительно
мгновенной оси.
Пример: качение цилиндра
r
r
r r
u A = uC + [w ´ R ]
r
r r
u A = [w ´ r ]
С течением времени мгновенная ось
непрерывно перемещается как в теле,
так и в пространстве.
06
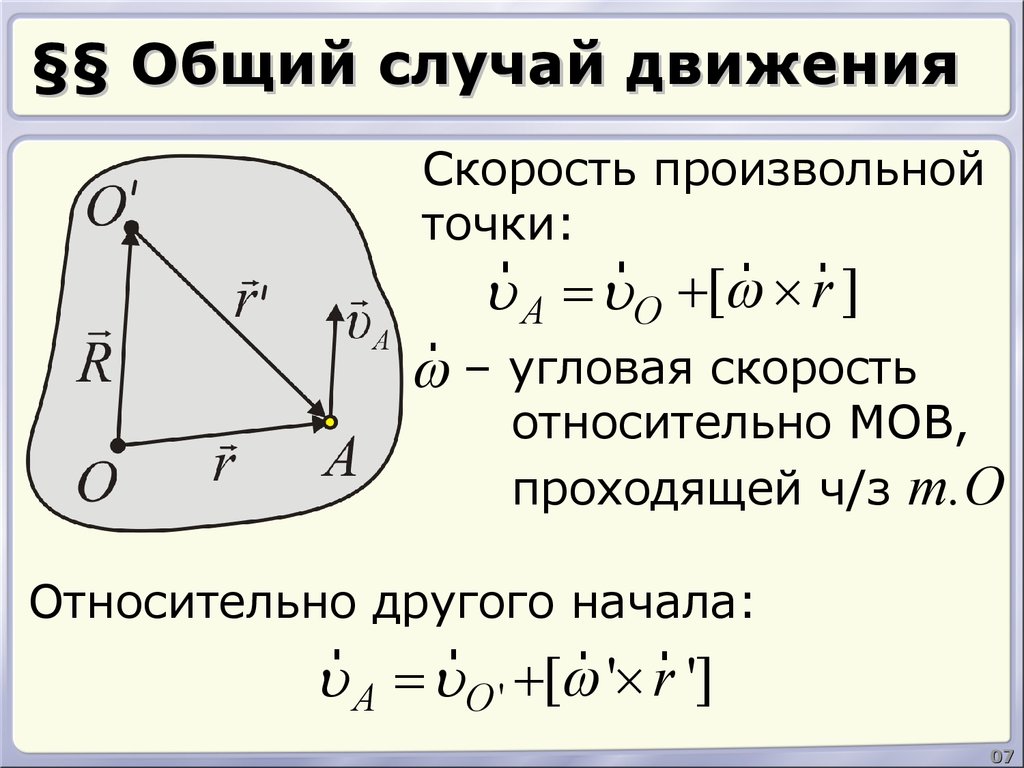
7. §§ Общий случай движения
Скорость произвольнойточки:
r r
r
r
u A = uO +[w ´ r ]
r
w – угловая скорость
относительно МОВ,
проходящей ч/з т.О
Относительно другого начала:
r r
r
r
u A = uO ' +[w '´ r ']
07
8.
rr r
r
r r
uO + [w ´ r ] = uO ' + [w '´ r ']
||
r
r r
r r r
uO + [w ´ R ] = [w ´ (r - r ')]
следовательно:
r r
r r
[w ´ r '] = [w '´ r ']
т.к.
r
r ' – произволен, то
r r
w =w'
– не зависит от выбора
т.О.
08
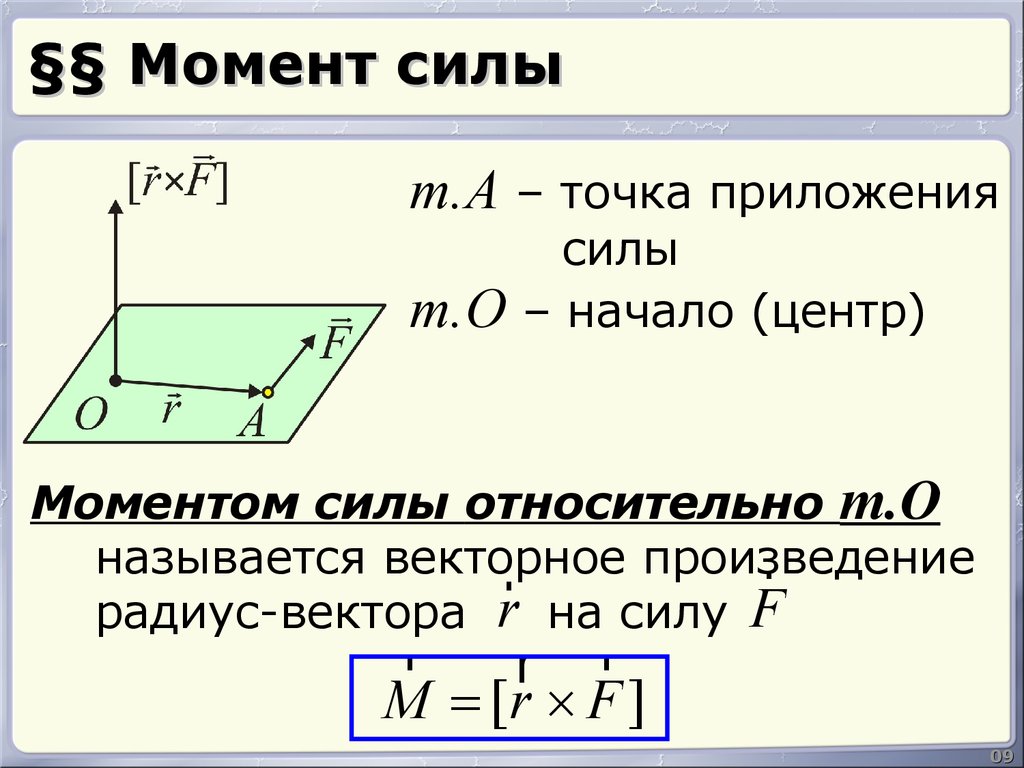
9. §§ Момент силы
т.A – точка приложеният.О
силы
– начало (центр)
Моментом силы относительно т.О
называется векторное
произведение
r
r
радиус-вектора r на силу F
r
r r
M = [r ´ F ]
09
10. Свойства:
1) при переносе силывдоль линии ее
действия момент
силы не изменяется
M = rF sin a = const
r r r
2) если F = F1 + F2 , то
r
r
r
r r
r r r
M = [r ´ F ] = [r ´ ( F1 + F2 )] = M1 + M 2
т.е. момент равнодействующей силы
равен сумме моментов сил.
10
11.
rM'
Вычислим момент
относительно
r
r нового начала
r r
r
r
M ' = [r '´ F ] = [(r - R )´ F ]
r
r r
= M - [R ´ F ]
r r
r
r
вдоль
M = M ' при R || F (т.е. смещение
r
линии действия силы) и F = 0
две равные и противоположно
направленные силы , линии
действия которых смещены
одна относительно другой,
называются парой сил.
11
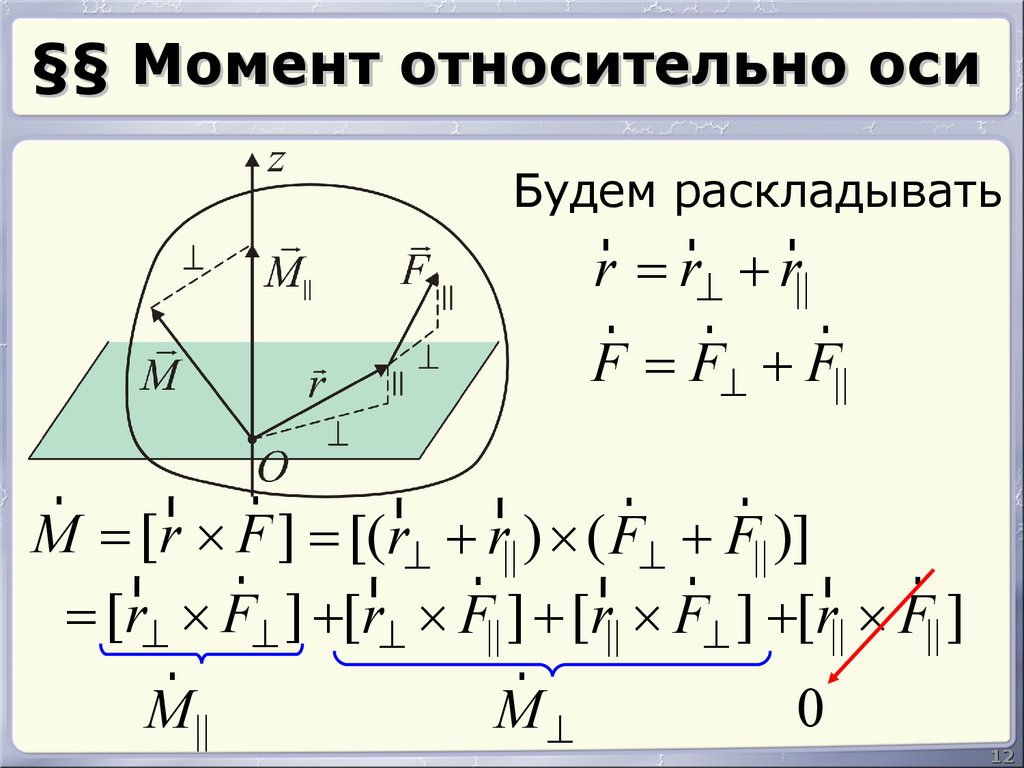
12. §§ Момент относительно оси
Будем раскладыватьr r r
r = r^ + r||
r r
r
F = F^ + F||
r
r
r
r r
r r
M = [r ´ F ] = [(r^ + r|| ) ´ ( F^ + F|| )]
r r
r r
r r
r r
= [r^ ´ F^ ] +[r^ ´ F|| ] + [r|| ´ F^ ] +[r|| ´ F|| ]
r
r
0
M ||
M^
12
13.
rr
r r
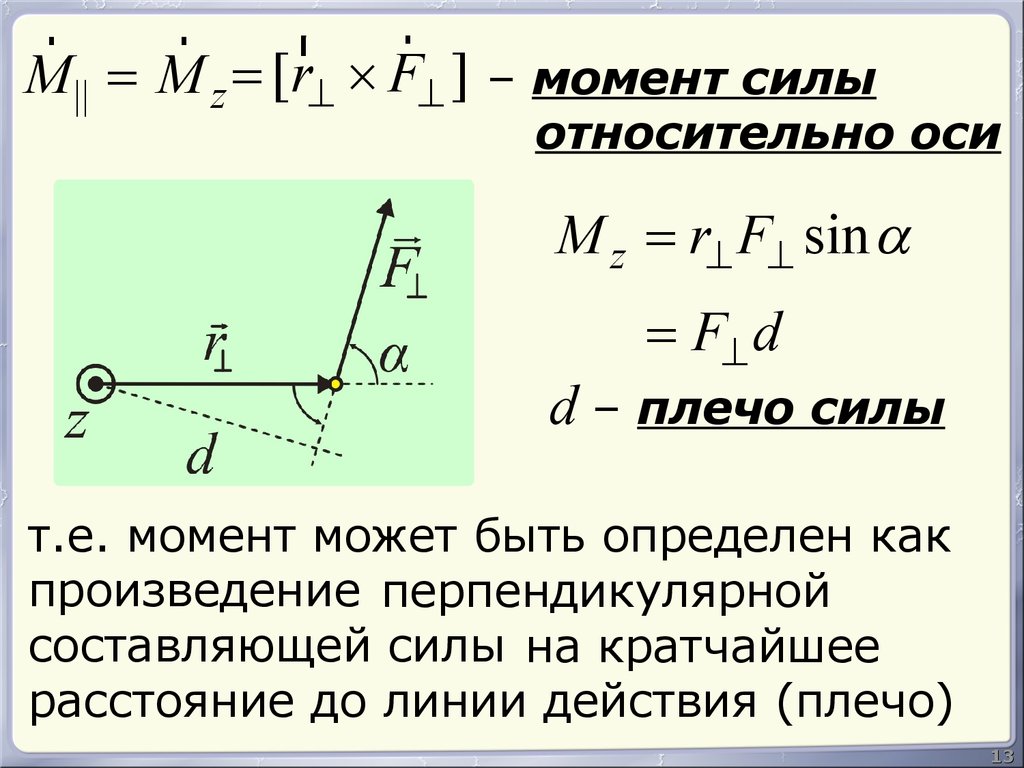
M || = M z = [r^ ´ F^ ]
– момент силы
относительно оси
M z = r^ F^ sin a
= F^ d
d – плечо силы
т.е. момент может быть определен как
произведение перпендикулярной
составляющей силы на кратчайшее
расстояние до линии действия (плечо)
13
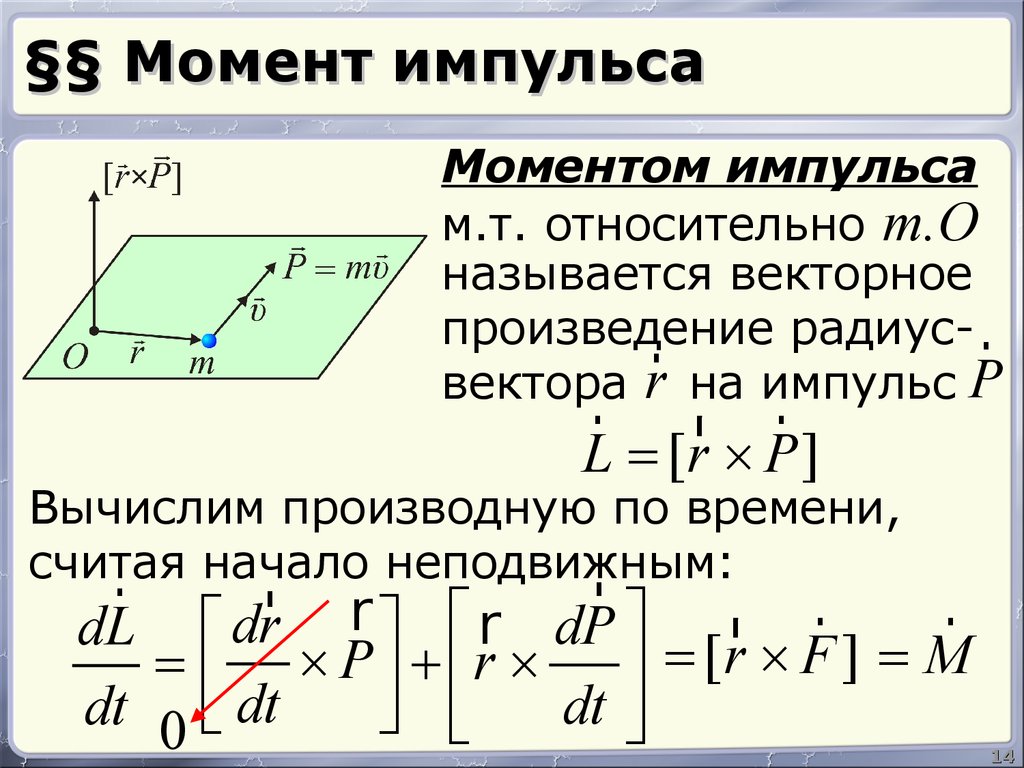
14. §§ Момент импульса
Моментом импульсам.т. относительно т.О
называется векторное
произведение
радиус- r
r
вектора r на импульс P
r r r
L = [r ´ P]
Вычислим производную по времени,
считая
r
r начало неподвижным:
r r
r
r
r
é
ù
dr
dL é
ù r dP = [r ´ F ] = M
= ê ´ P ú + êr ´ ú
dt û
dt 0 ë dt
û ë
14
15.
rdL r
=M
dt
– уравнение моментов
производная по времени м.и. м.т.
относительно неподвижного начала
равна моменту действующей силы
относительно того же начала
N частиц
r
r int r ext
dLi
= Mi + Mi
dt
Рассмотрим систему из
15
16.
суммируя уравнения, получаем:r
r ext
r int
dLi
å dt = å M i +å M i
0
r
r
dL r ext
dP r ext
=M
=F
dt
dt
производная по времени м.и. с.м.т.
относительно неподвижного начала
равна геометрической сумме моментов
внешних сил относительно этого начала
16
17. Закон сохранения момента импульса
если момент внешних сил относительнонеподвижного начала равен нулю,
то м.и. системы относительно того же
начала остается постоянным во времени
в проекции на ось:
dLz
ext
= Mz
dt
если момент внешних сил относительно
оси равен нулю, то м.и. системы
относительно той же оси остается
постоянным.
17
18. §§ Работа и кин. энергия
rr
dA = ( F^ × dS )
= F^ r^ dj sin a
= M z dj
При повороте тела совершается работа:
r r
dA = ( M × dj )
18
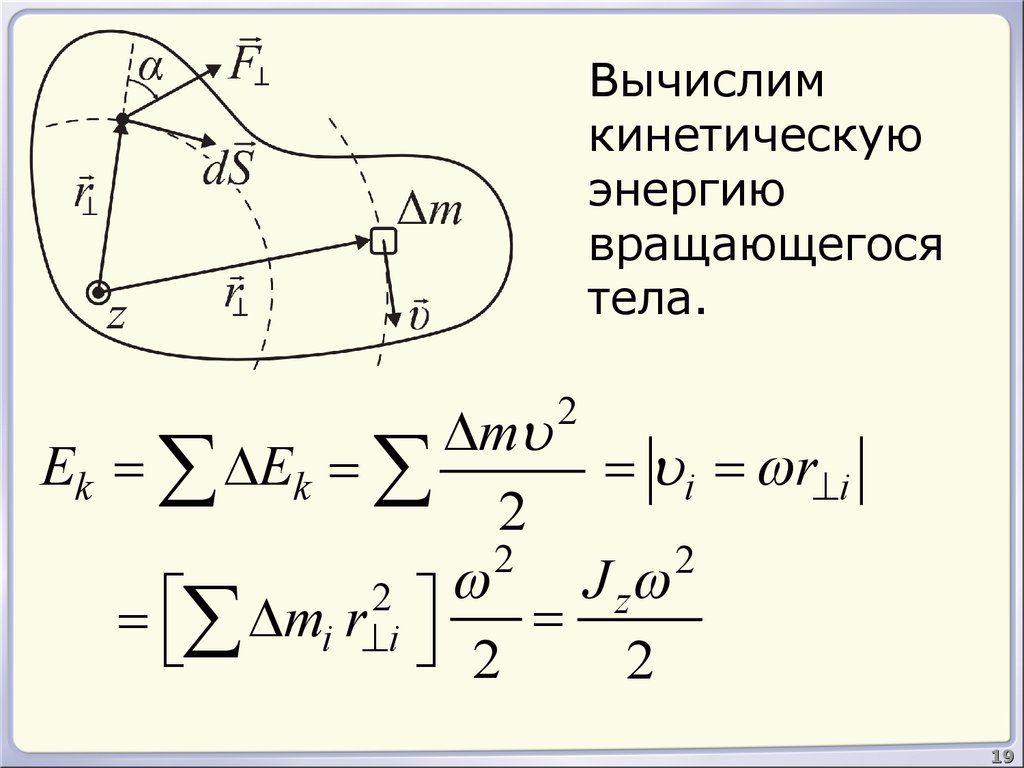
19.
Вычислимкинетическую
энергию
вращающегося
тела.
2
Dmu
Ek = å DEk = å
= ui = w r^i
2
2
2
w
J
w
2
z
=
= éëå Dmi r^i ùû
2
2
19
20.
Jz =2
m r^ – момент инерции м.т. массой
m
r^ – расстояние до оси z
Jz = å
2
mi r^i – момент инерции с.м.т.
Величина Jz – является мерой инерции
тела (точки) при вращении.
J zw
Ek =
2
2
2
muO
– для вращательного
движения
J zw
Ek =
+
2
2
2
– для плоского
движения
20
21. §§ Уравнение динамики
Пусть м.т. двигается по окружности:L = r^ mu =
2
mr^ w
= Jw
r
r
L = Jw
подставим в уравнение моментов
r
r
d
( Jw) = M
dt
r
dw r
J
=M
dt
r r
Je = M
для неизменной
с.м.т. (атт)
– это основное уравнение динамики
вращательного движения (ОУДВД)
21
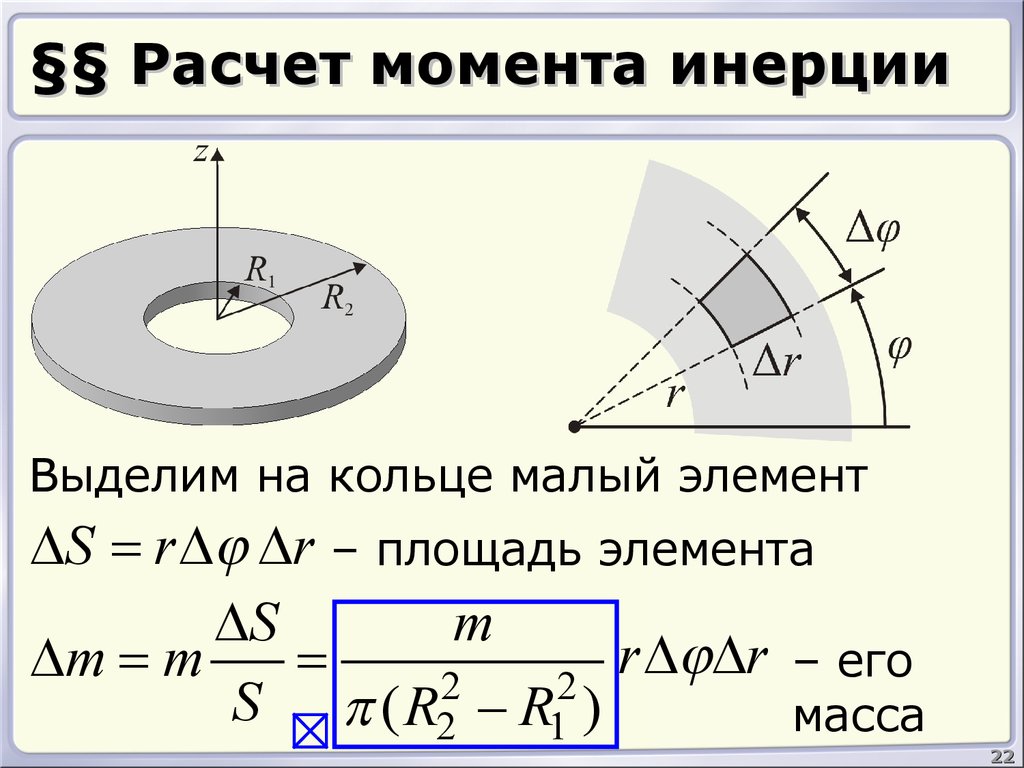
22. §§ Расчет момента инерции
Выделим на кольце малый элементдо оси элемента
DSr –= расстояние
r Dj Dr – площадь
Dr – размер
по
r
DS
m
j =– mугловая
r
D
j
D
r
Dm
= координата
–
его
2
2
S p размер
( R2 - R1 )
масса
Dj – угловой
22
23.
23
DJ z = Dmr =
r DjDr
J z = å DJ z =
å Dj å r Dr
3
0<j <2p
2p
=
m
=
2p
2
2
p ( R2 - R1 )
ò
dj
R1<r < R2
R2
ò
3
r dr
0
R1
4
( R2
4
- R1 )
4
1
2
2
= m( R2 + R1 )
2
23
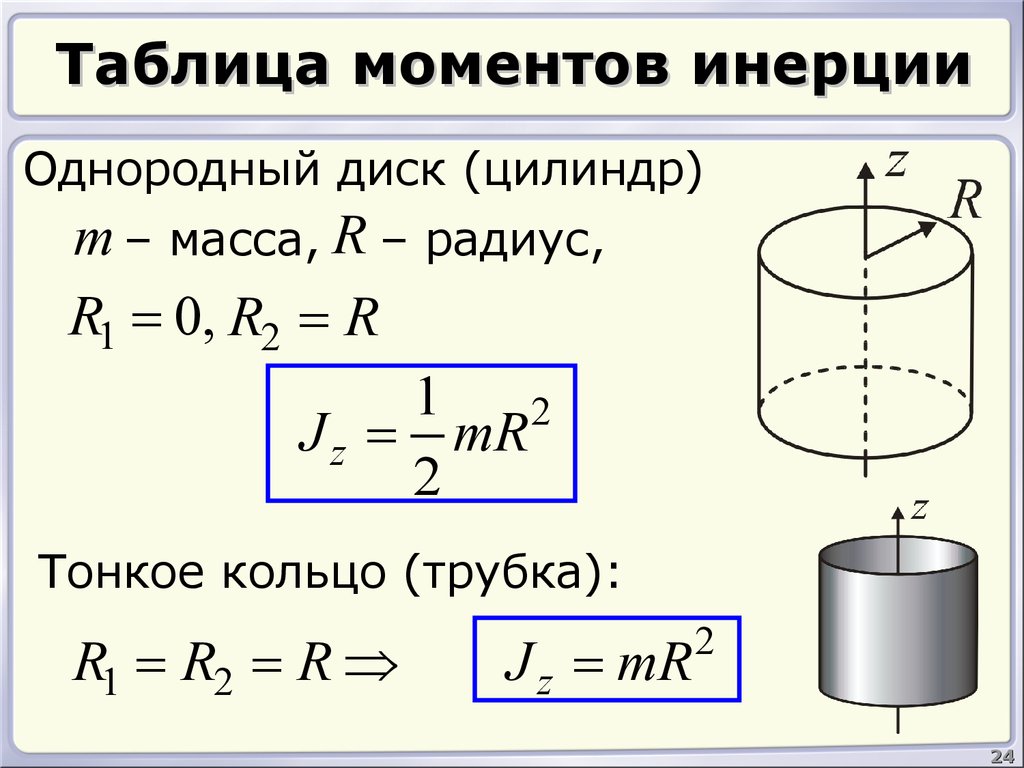
24. Таблица моментов инерции
Однородный диск (цилиндр)m – масса, R – радиус,
R1 = 0, R2 = R
1
2
J z = mR
2
Тонкое кольцо (трубка):
R1 = R2 = R Þ
J z = mR
2
24
25.
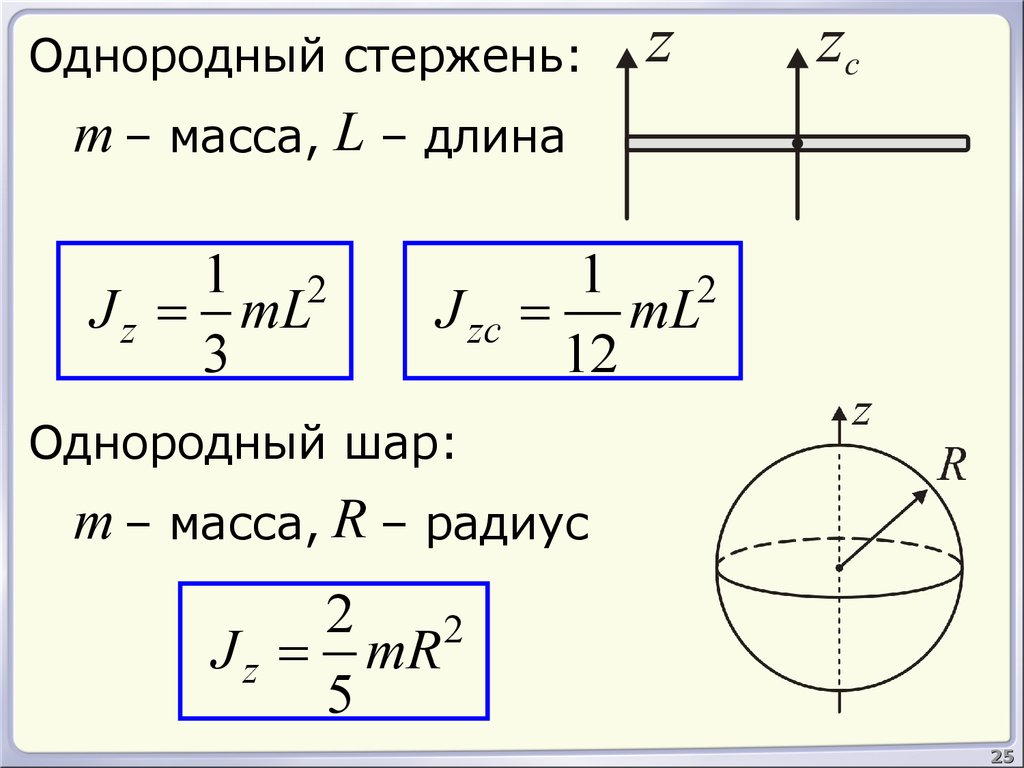
Однородный стержень:m – масса, L – длина
1 2
J z = mL
3
J zc
1
2
= mL
12
Однородный шар:
m – масса, R – радиус
2
2
J z = mR
5
25
26.
Замечания:1) момент инерции для тел простой
формы:
J z = b mx
b
x
2
– зависит от выбора оси
z
– характерный размер
2) в справочниках приведены моменты
инерции относительно осей,
проходящих через центр масс
26
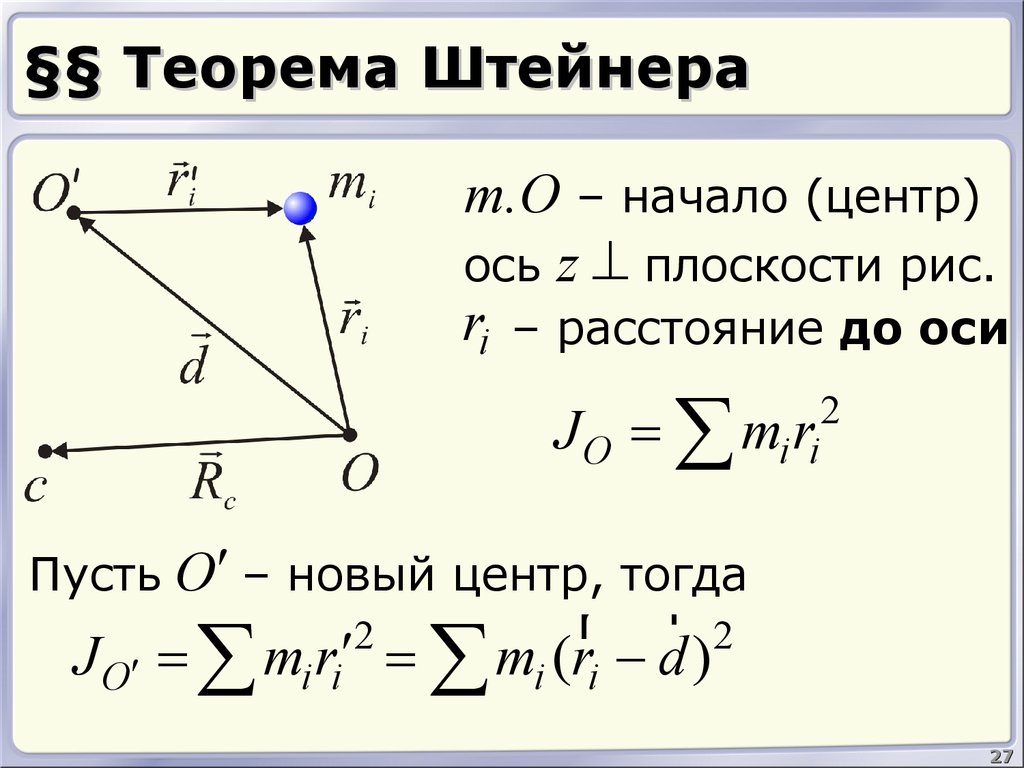
27. §§ Теорема Штейнера
т.О – начало (центр)ось z ^ плоскости рис.
ri – расстояние до оси
J O = å mi ri
2
Пусть O¢ – новый центр, тогда
r
r
2
2
¢
J O¢ = å mi ri = å mi (ri - d )
27
28.
rr
2
2
= å mi ri -2 å mi ri × d + å mi d
r
mRc
r r
2
= J O -2m( Rc × d ) + md
r
Если Rc = 0 (ось проходит через центр
(
)
инерции системы), то
JO ' = Jc
2 – теорема
+ md
Гюйгенса-Штейнера
28
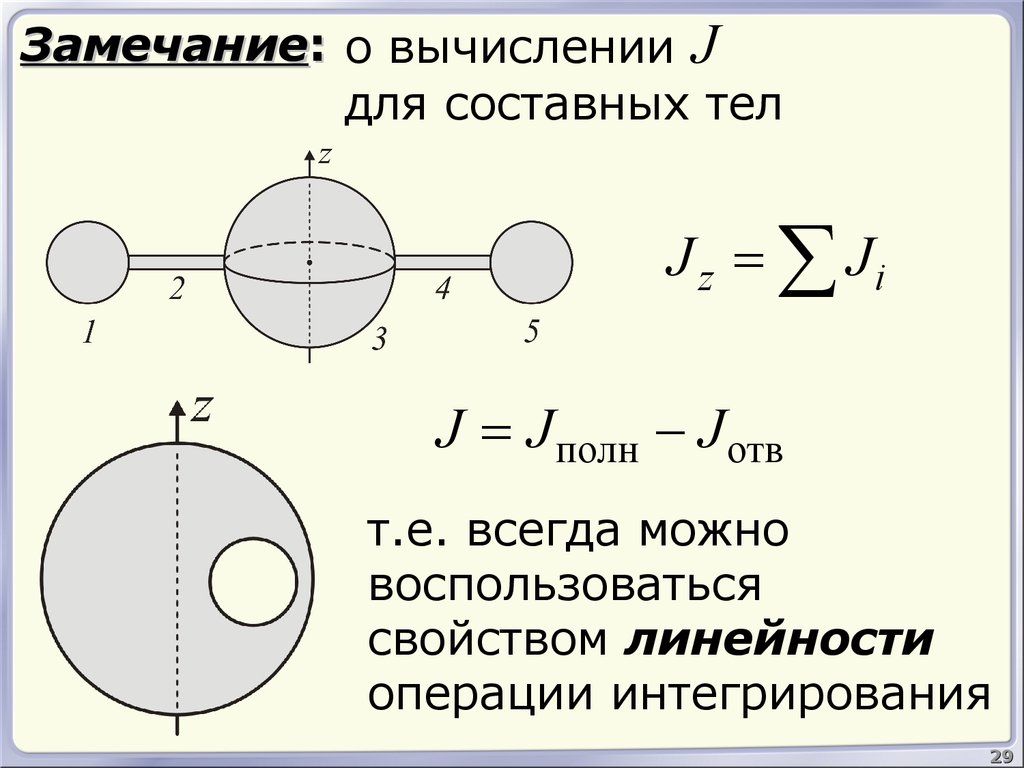
29. Замечание:
о вычислении Jдля составных тел
J z = å Ji
J = J полн - J отв
т.е. всегда можно
воспользоваться
свойством линейности
операции интегрирования
29
















 Физика
Физика








