Проецирование точки. Лекция 1

1.

Введение

2.

1 Предмет
“ Начертательная геометрия “

3.

2 Краткий исторический
очерк
См. учебник Б.Ф.Тарасов
и др.
“ Начертательная
геометрия “

4.

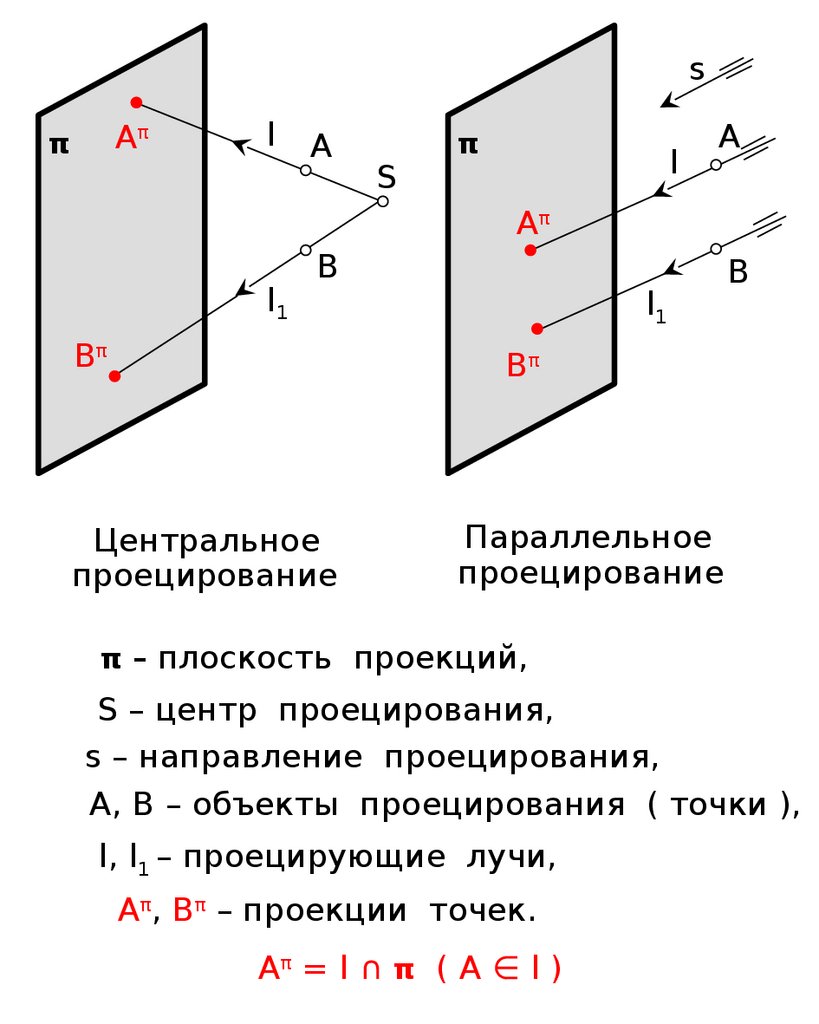
3 Способы проецирования.
Проекция точки

5.

s
Aπ
π
l
A
S
π
l
A
Aπ
l1
B
Bπ
l1
B
Bπ
Центральное
проецирование
Параллельное
проецирование
π – плоскость проекций,
S – центр проецирования,
s – направление проецирования,
A, B – объекты проецирования ( точки ),
l, l1 – проецирующие лучи,
Aπ, Bπ – проекции точек.
Aπ = l ∩ π ( A ∈ l )

6.

4 Инвариантные свойства
параллельного проецирования

7.

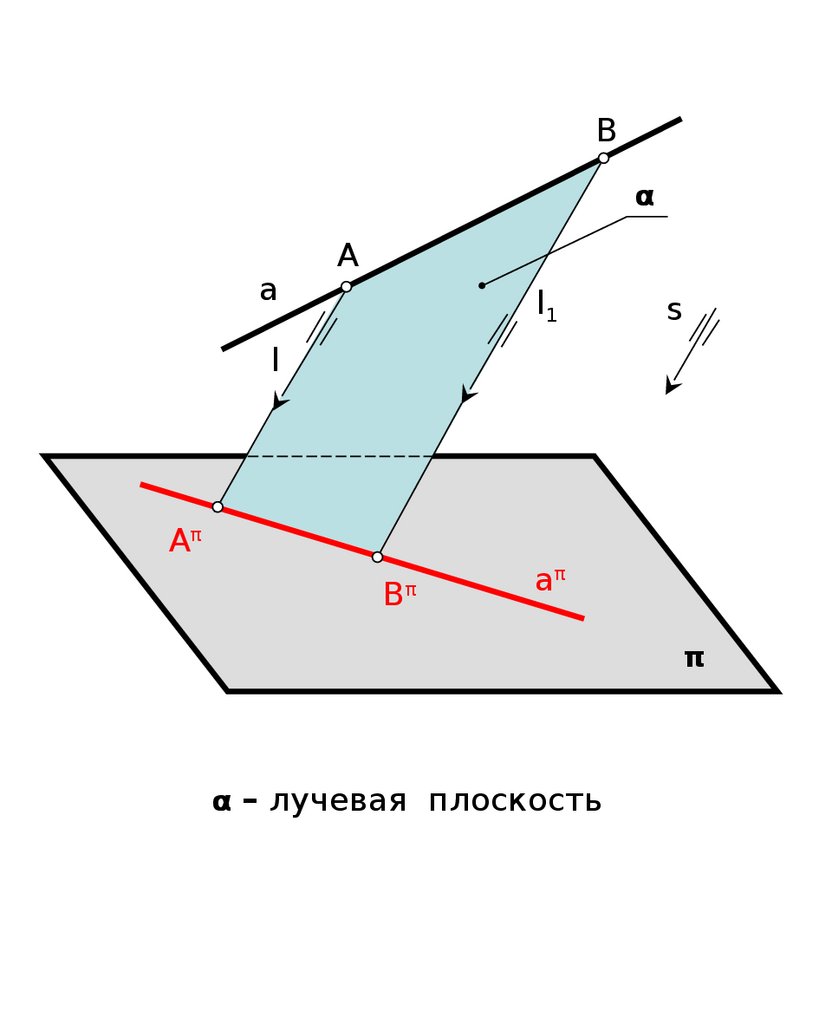
4.1 Проекция точки есть
точка.

8.

4.2 Проекция прямой в
общем случае прямая.

9.

B
α
a
A
l1
s
l
Aπ
Bπ
aπ
π
α – лучевая плоскость

10.

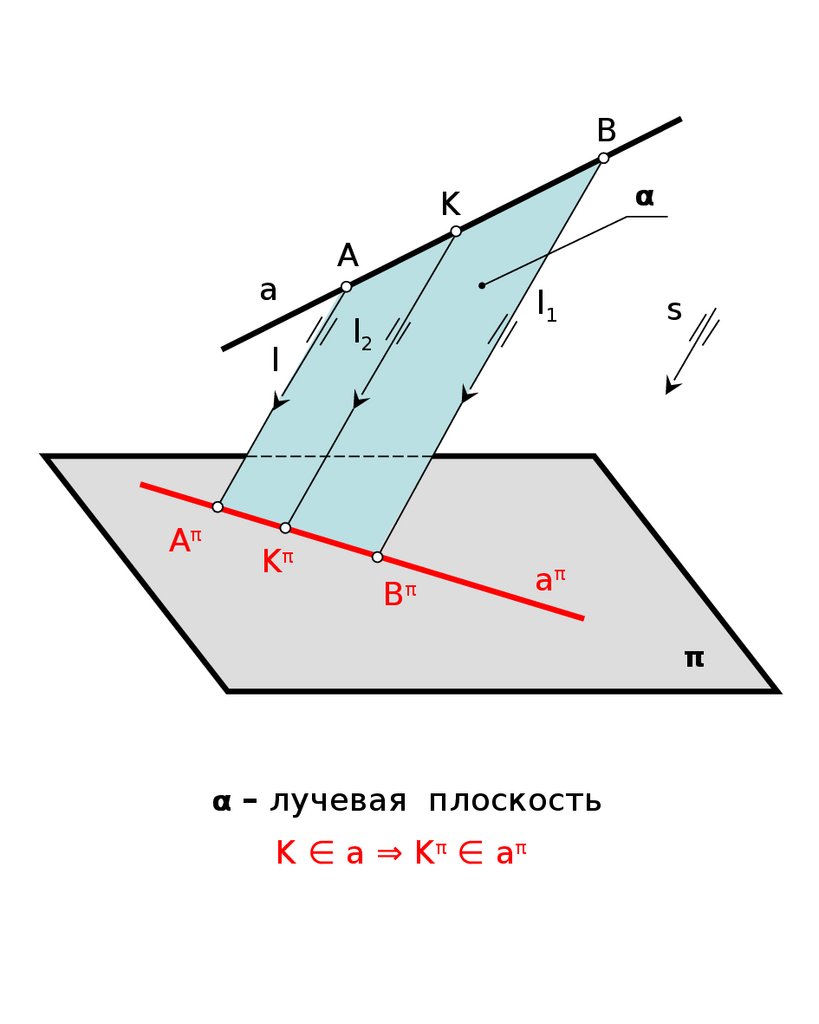
4. 3 Если точка принадлежит
прямой, то и проекция этой
точки принадлежит проекции
прямой.

11.

B
α
K
a
l
Aπ
Kπ
A
l1
l2
Bπ
s
aπ
π
α – лучевая плоскость
K ∈ a ⇒ Kπ ∈ a π

12.

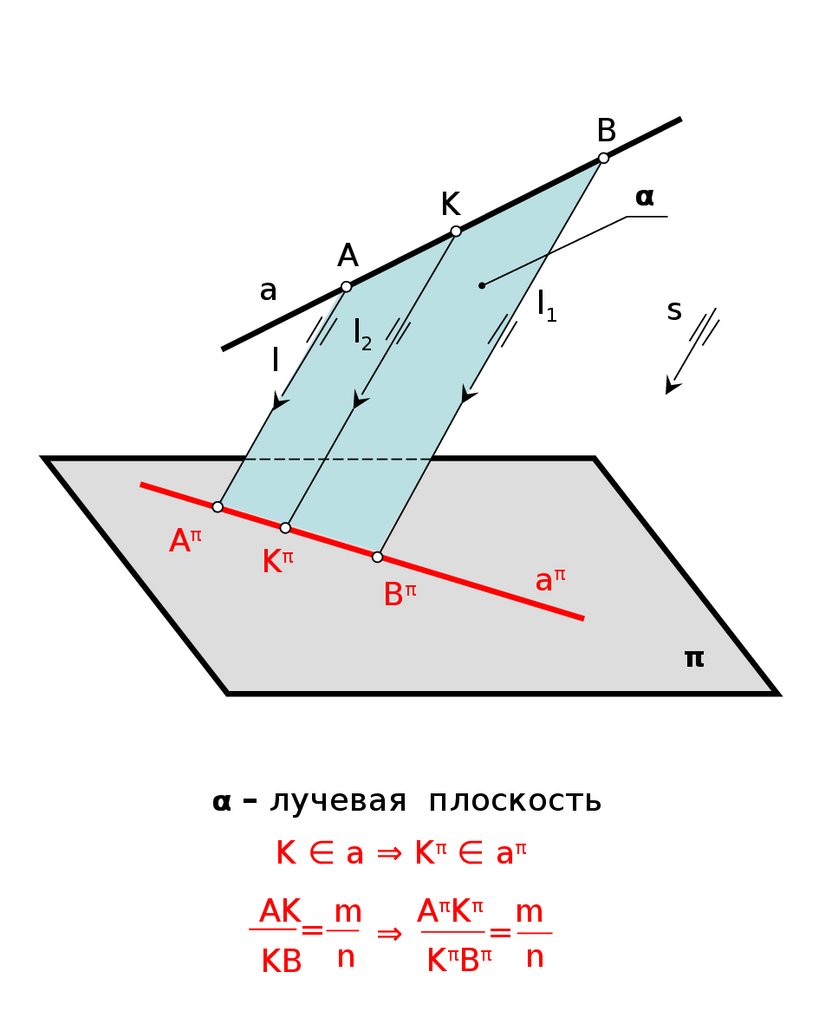
4.4 Если точка делит
отрезок прямой в каком-то
отношении, то и проекция
этой точки делит проекцию
отрезка в таком же
отношении.

13.

B
α
K
a
l
Aπ
Kπ
A
l1
l2
Bπ
s
aπ
π
α – лучевая плоскость
K ∈ a ⇒ Kπ ∈ a π
AK m
AπKπ m
=
=
⇒
π π
n
KB n
KB

14.

4.5 Проекция точки пересечения прямых есть точка
пересечения проекций этих
прямых.

15.

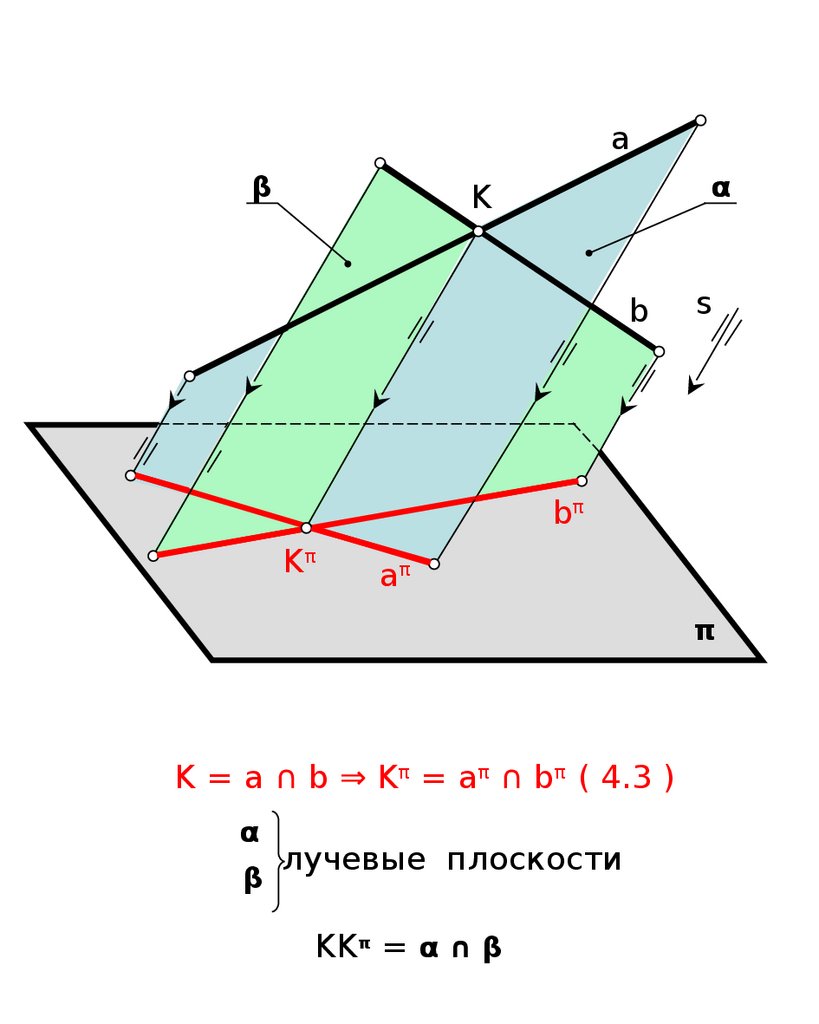
a
β
α
K
b
s
bπ
Kπ
aπ
π
K = a ∩ b ⇒ Kπ = aπ ∩ bπ ( 4.3 )
α
β
лучевые плоскости
KKπ = α ∩ β

16.

4.6 Проекции параллельных
прямых параллельны.

17.

D
B
β
A
C
α
s
Cπ
Aπ
Bπ
Dπ
π
AB II CD ⇒ AπBπ II CπDπ ( α II β )
α
лучевые плоскости
β

18.

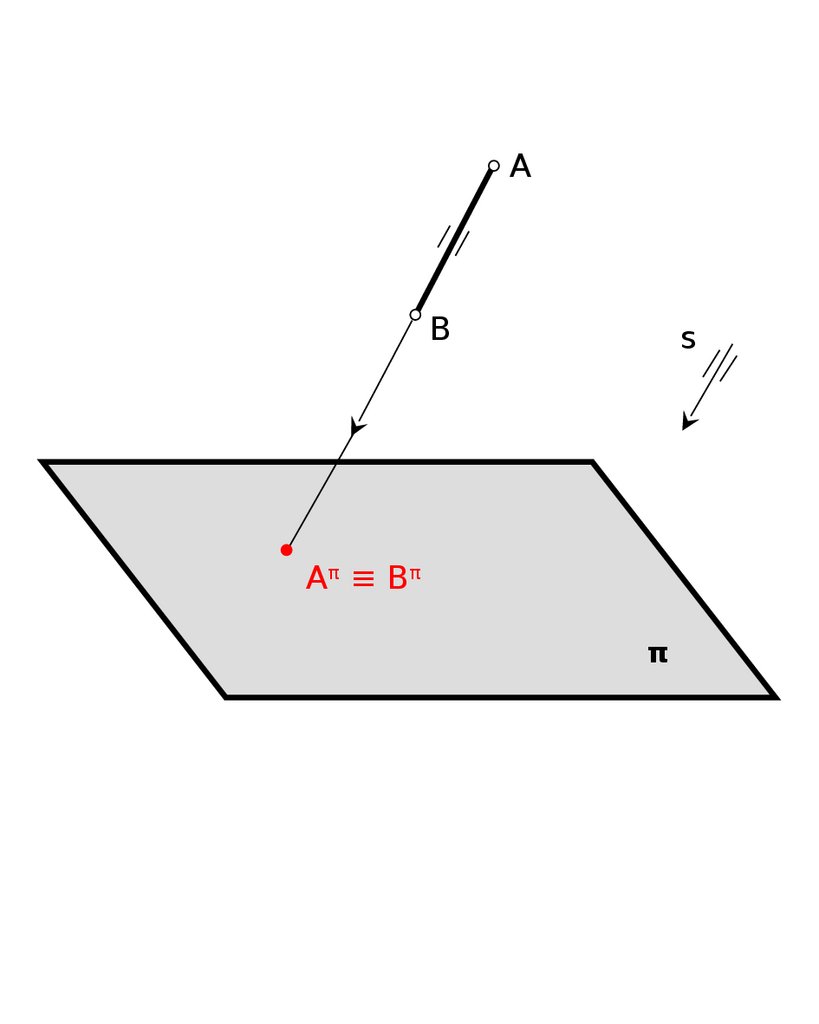
4.7 Прямая, параллельная
аправлению проецирования,
проецируется в точку.

19.

A
B
s
Aπ ≡ Bπ
π

20.

4.8 Плоский многоугольник
в общем случае проецируется
в многоугольник с тем же
числом вершин.

21.

B
C
A
s
Bπ
Aπ
Cπ
π

22.

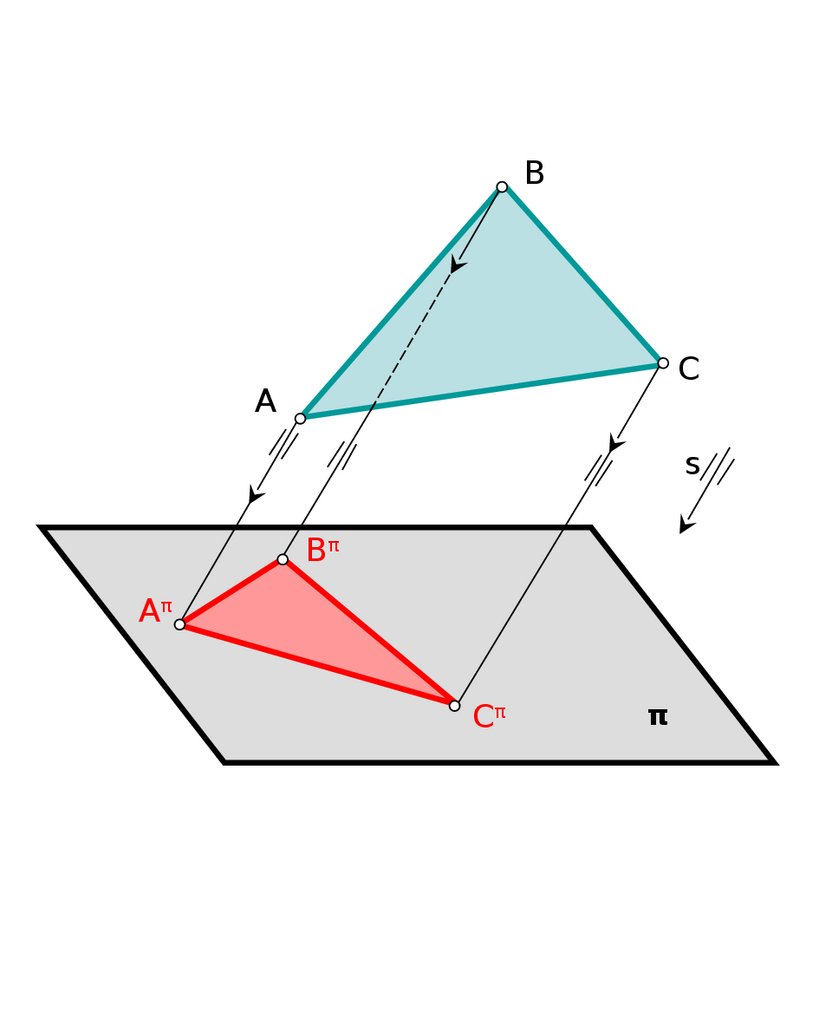
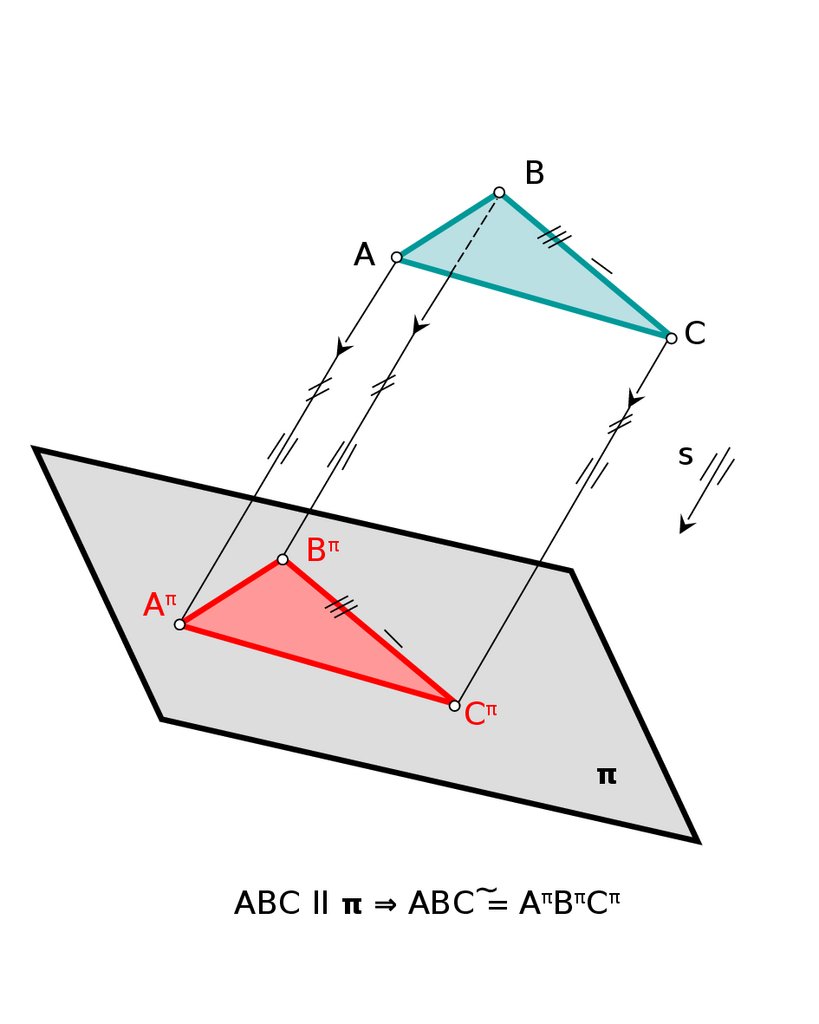
4.9 Проекция плоской
фигуры, параллельной плоскос
роекций, конгруэнтна этой
фигуре.

23.

B
A
C
s
Bπ
Aπ
Cπ
π
ABC II π ⇒ ABC∼= AπBπCπ

24.

4.9.1 Проекция отрезка
рямой, параллельной плоскос
роекций, конгруэнтна и
араллельна самому отрезку.

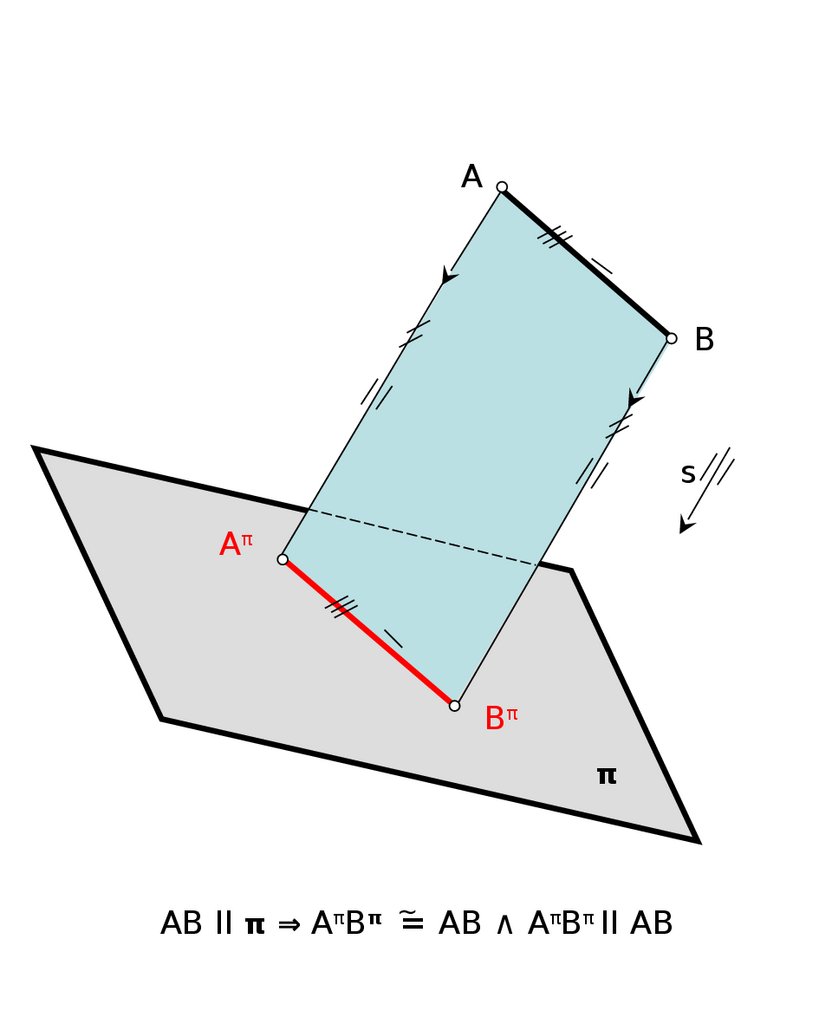
25.

A
B
s
Aπ
Bπ
π
AB II π ⇒ AπBπ ∼
= AB ∧ AπBπ II AB

26.

4.9.2 Проекция угла,
тороны которого параллельны
плоскости проекций, конгрунтна этому углу.

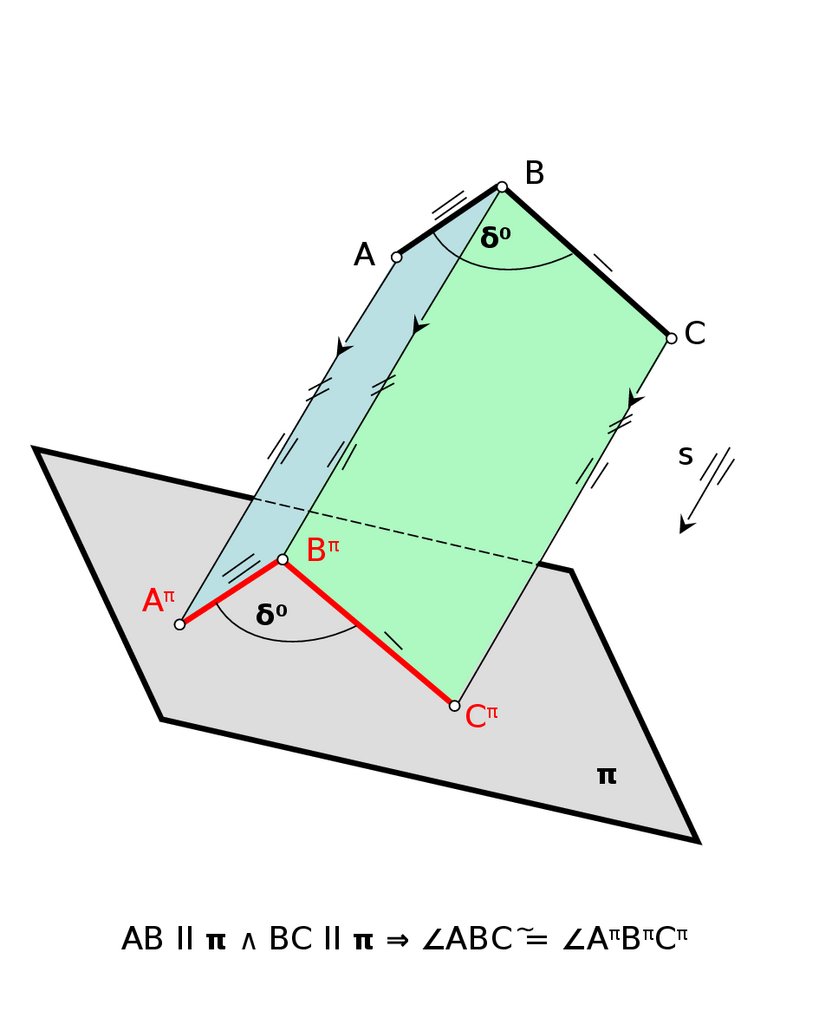
27.

B
A
δ0
C
s
Bπ
Aπ
δ0
Cπ
π
AB II π ∧ BC II π ⇒ ∠ABC ∼= ∠AπBπCπ

28.

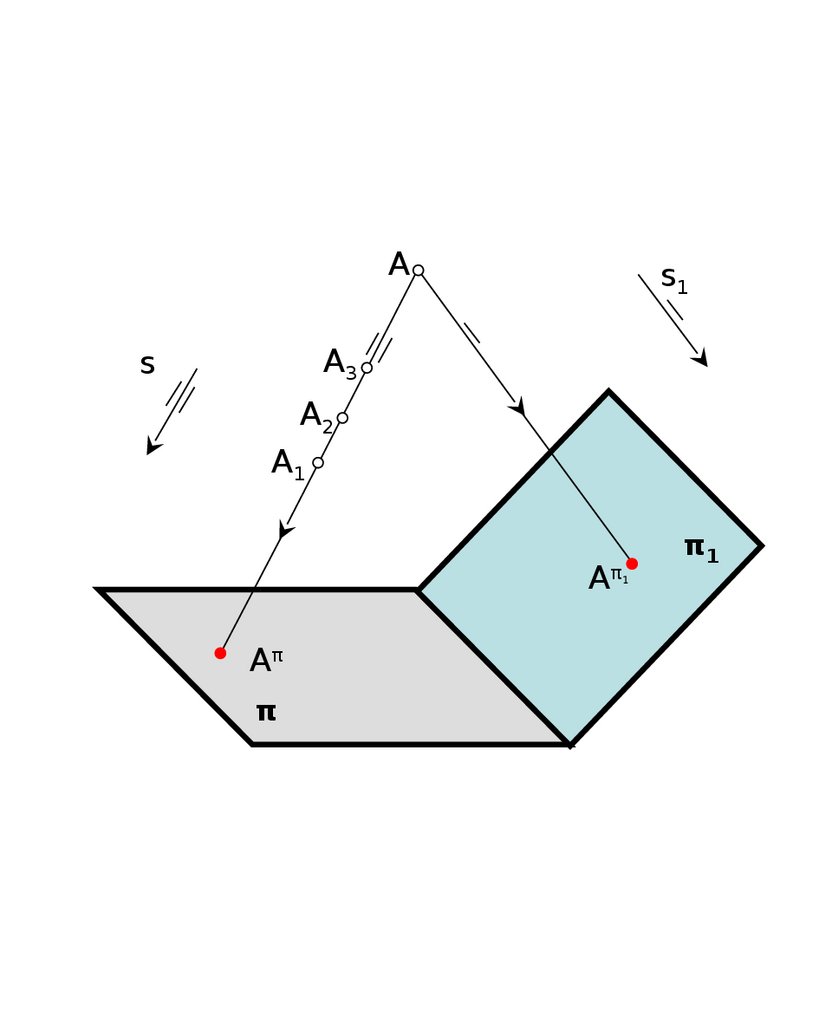
5 Обратимость чертежа

29.

A
s1
A3
s
A2
A1
Aπ
1
Aπ
π
π1

30.

6 Ортогональное
проецирование

31.

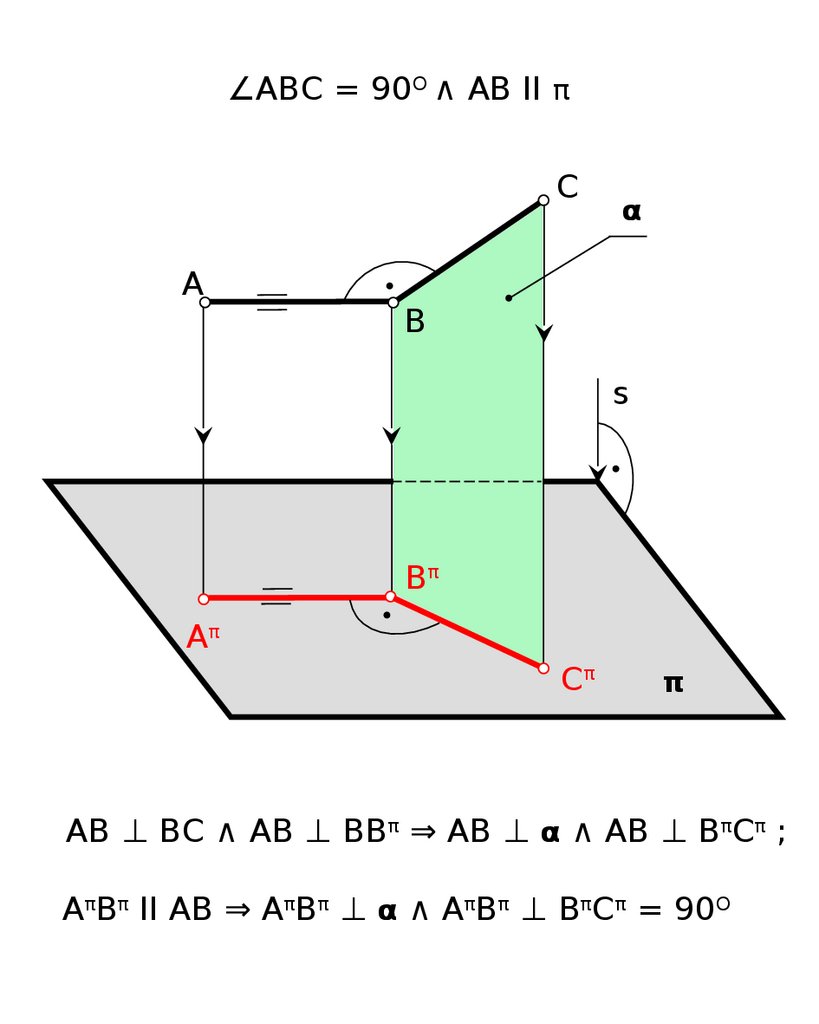
∠ABC = 90O ∧ AB II π
C
A
α
B
s
Bπ
Aπ
Cπ
π
AB ⊥ BC ∧ AB ⊥ BBπ ⇒ AB ⊥ α ∧ AB ⊥ BπCπ ;
AπBπ II AB ⇒ AπBπ ⊥ α ∧ AπBπ ⊥ BπCπ = 90O

32.

7 Система трех плоскостей
проекций.
Эпюра Монжа

33.

Эпюра Монжа 1

34.

π1 – горизонтальная плоскость проекций,
π2 – фронтальная плоскость проекций,
π3 – профильная плоскость проекций,
O - начало координат,
Ox – ось абсцисс,
Oy – ось ординат,
Oz – ось аппликат,
I, II, III, IV – пространственные углы.

35.

Эпюра Монжа 2

36.

I Точка

37.

Эпюра Монжа 3